高中数学椭圆及其标准方程教案 3页

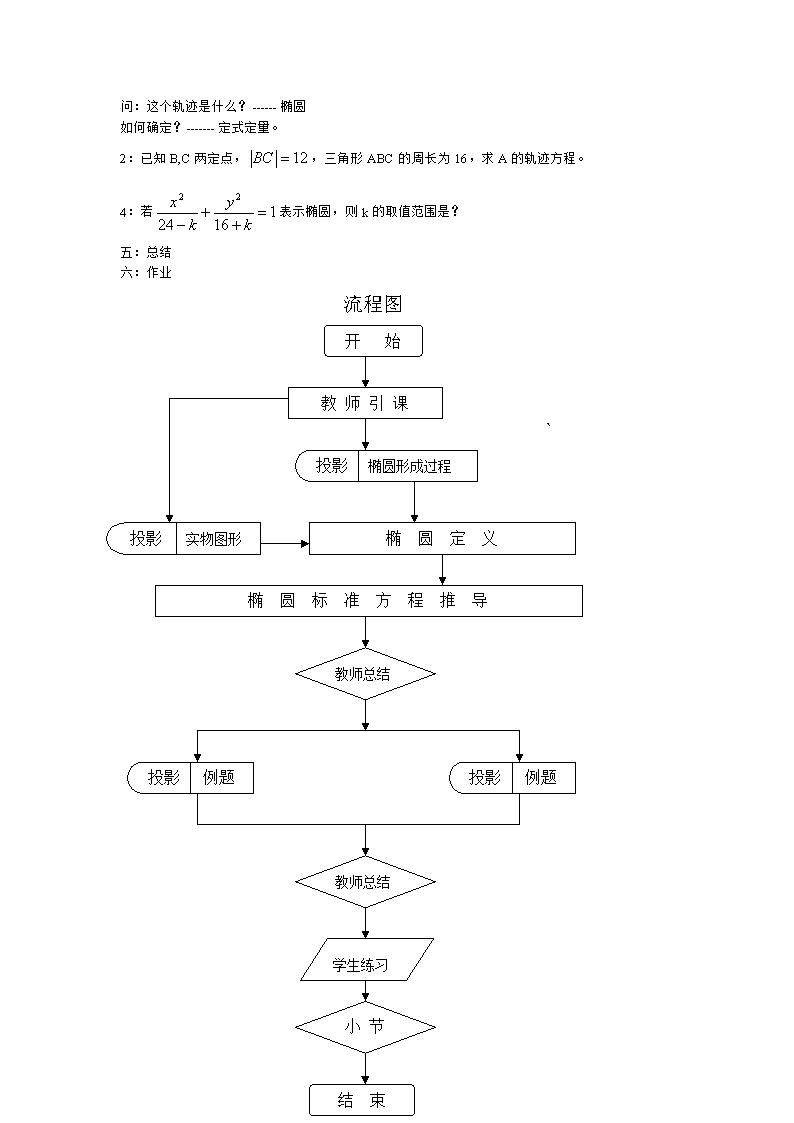
教学章节：椭圆及其标准方程教学目标：知识目标：1：熟练掌握椭圆的定义。2：熟练掌握椭圆的标准方程，会根据所给的条件画出椭圆的草图并确定椭圆的标准方程。能力目标：（1）重视基础知识的教学、基本技能的训练和能力的培养；（2）启发学生能够发现问题和提出问题，善于独立思考，学会分析问题和创造地解决问题；（3）通过教师指导发现知识结论，培养学生抽象概括能力和逻辑思维力；教学重点：椭圆的定义及标准方程。教学难点：椭圆的定义及标准方程的推导。教学过程：一：椭圆概念的引入：1：举例：（1）天体行星和卫星运行的轨道。（2）立体几何中作园的一种直观图。2：手工操作演示椭圆的形成：取一条定长的细绳，把它的两端固定在画图板上的F1,F2两点，当绳长大于两点间的距离时，用铅笔把绳子拉近，使笔尖在图板上慢慢移动，就可以画出一个椭圆。分析：（1）轨迹上的点是怎么来的？（2）在这个运动过程中，什么是不变的？答：两个定点，绳长。即不论运动到何处，绳长不变（即轨迹上与两个定点距离之和不变）3：由此总结椭圆定义：平面内与两个定点F1,F2的距离之和等于常熟（大于）的点的轨迹叫作椭圆，这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距。4：说明（1）注意椭圆定义中容易遗漏的两处地方：（2）两个定点------两点间距离确定。绳长------轨迹上任意点到两定点距离和确定。（3）思考：在同样的绳长下，两定点间距离较长，则所画出的椭圆较扁（极限：线段）。在同样的绳长下，两定点间距离较短，则所画出的椭圆较圆（极限：圆）。注意到条件：由此，椭圆的形状与两定点间距离，绳长有关。（为下面离心率概念作铺垫）二：根据定义推导椭圆标准方程：1：复习求轨迹方程的基本步骤：2：推导：取过焦点的直线为x轴，线段的垂直平分线为y轴。设P（x,y）为椭圆上的任意一点，椭圆的焦距是2c（c>0）.则：，又设M与F1,F2距离之和等于2a（常数），\n，化简，得：，由定义令代入，得：，两边同除得：，此即为椭圆的标准方程。它所表示的椭圆的焦点在x轴上，焦点是，中心在坐标原点的椭圆方程。其中注意若坐标系的选取不同，可得到椭圆的不同的方程，说明：（1）其中：2a为椭圆上任意点到焦点的距离之和这个定值。焦距2c，而由（2）如果椭圆的焦点在y轴上（选取方式不同，调换x,y轴）焦点则变成：只要将此方程中的x,y调换，即可得：，此也是椭圆的标准方程。三：巩固练习：1：判断下列方程是否表上椭圆，若是，求出a,b,c的值。①②③④变形为：总结：注意到a2>b2，则可以根据分母的大小，判断其焦点在哪个坐标轴上。2：求三量：四：例题讲解：1：平面内两定点的距离是8，写出到这两定点的距离之和是10的点的轨迹方程。\n问：这个轨迹是什么？------椭圆如何确定？-------定式定量。2：已知B,C两定点，，三角形ABC的周长为16，求A的轨迹方程。4：若表示椭圆，则k的取值范围是？五：总结六：作业流程图开始教师引课椭圆标准方程推导椭圆定义投影实物图形投影`椭圆形成过程教师总结例题2投影例题1投影结束小节教师总结学生练习