高中数学必修一幂函数教案 6页

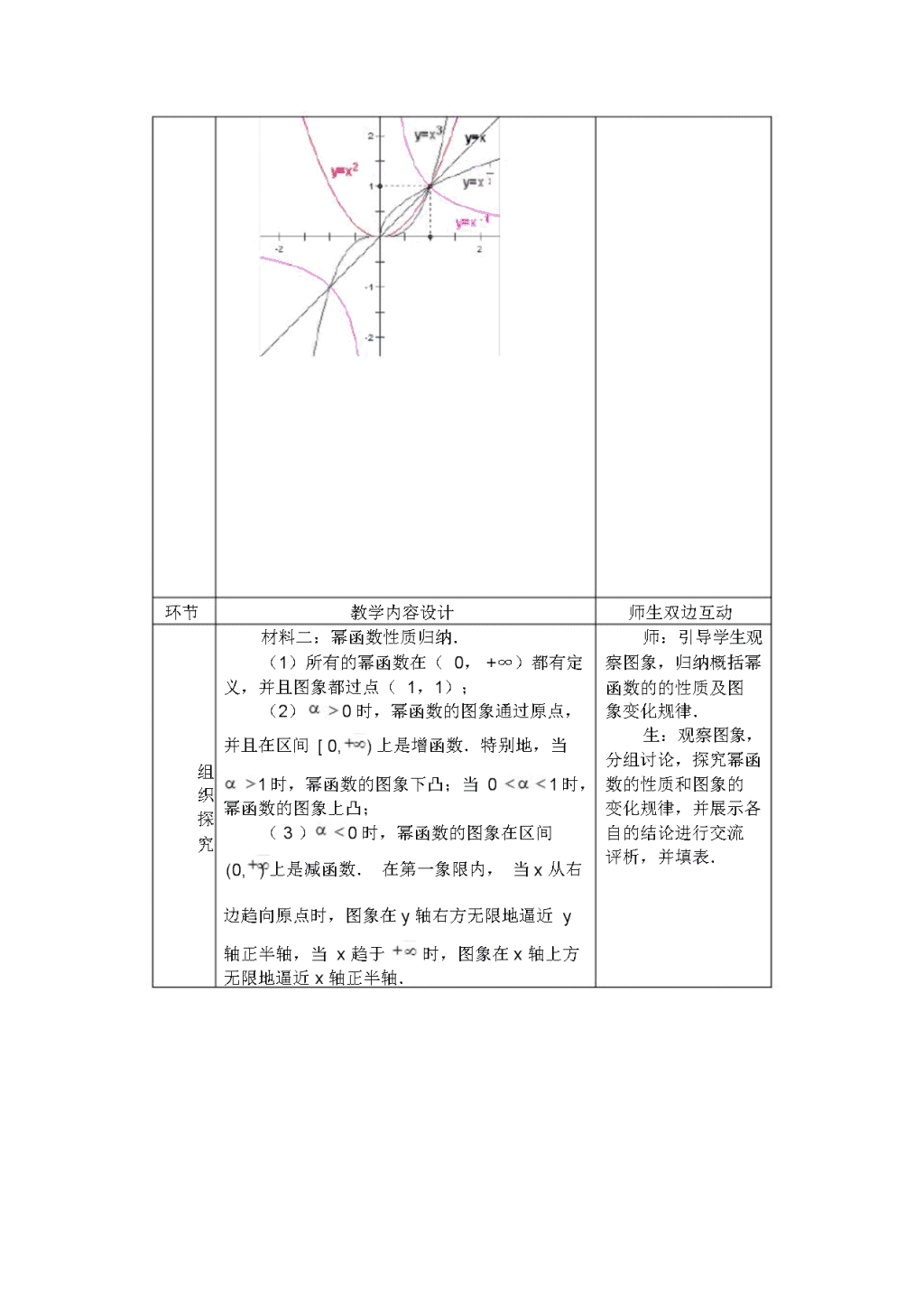
高中数学必修一幂函数教案教学目标：知识与技能通过具体实例了解幂函数的图象和性质，并能进行简单的应用．过程与方法能够类比研究一般函数、指数函数、对数函数的过程与方法，来研究幂函数的图象和性质．情感、态度、价值观体会幂函数的变化规律及蕴含其中的对称性．教学重点：重点从五个具体幂函数中认识幂函数的一些性质．难点画五个具体幂函数的图象并由图象概括其性质，体会图象的变化规律．教学程序与环节设计：创设情境问题引入．组织探究幂函数的图象和性质．尝试练习幂函数性质的初步应用．巩固反思复述幂函数的图象规律及性质．作业回馈幂函数性质的初步应用．课外活动利用图形计算器或计算机探索一般幂函数的图象规律．\n教学过程与操作设计：环节教学内容设计阅读教材P90的具体实例（1）~（5），思考下列问题：1．它们的对应法则分别是什么？2．以上问题中的函数有什么共同特征？创（答案）设情1．（1）乘以1；（2）求平方；（3）求师生双边互动生：独立思考完成引例．师：引导学生分析归纳概括得出结论．师生：共同辨析这种新函数与指数函数的异同．境立方；（4）开方；（5）取倒数（或求－1次方）．2．上述问题中涉及到的函数，都是形如yx的函数，其中x是自变量，是常数．材料一：幂函数定义及其图象．师：说明：一般地，形如幂函数的定义yx(aR)来自于实践，它同指数函数、对数函数一的函数称为幂函数，其中为常数．样，也是基本初等函下面我们举例学习这类函数的一些性质．数，同样也是一种作出下列函数的图象：“形式定义”的函1数，引导学生注意辨（1）yx；（2）yx2；（3）yx2；析．组（4）yx1；（5）yx3．织探[解]1列表（略）究○2图象○生：利用所学知识和方法尝试作出五个具体幂函数的图象，观察所图象，体会幂函数的变化规律．师：引导学生应用画函数的性质画图象，如：定义域、奇偶性．师生共同分析，强调画图象易犯的错误．\n环节教学内容设计师生双边互动材料二：幂函数性质归纳．师：引导学生观（1）所有的幂函数在（0，+∞）都有定察图象，归纳概括幂义，并且图象都过点（1，1）；函数的的性质及图（2）0时，幂函数的图象通过原点，象变化规律．并且在区间[0,)上是增函数．特别地，当生：观察图象，分组讨论，探究幂函组1时，幂函数的图象下凸；当01时，数的性质和图象的织幂函数的图象上凸；变化规律，并展示各探（3）0时，幂函数的图象在区间自的结论进行交流究评析，并填表．(0,)上是减函数．在第一象限内，当x从右边趋向原点时，图象在y轴右方无限地逼近y轴正半轴，当x趋于时，图象在x轴上方无限地逼近x轴正半轴．\n材料三：观察与思考观察图象，总结填写下表：yxyx2yx31yx1yx2定义域值域奇偶性单调性定点材料五：例题[例1]（教材P92例题）[例2]比较下列两个代数值的大小：（1）(a1)1.5，a1.522（2）(2a2)3，232[例3]讨论函数yx3的定义域、奇偶性，作出它的图象，并根据图象说明函数的单调性．环节呈现教学材料1．利用幂函数的性质，比较下列各题中两个幂的值的大小：33（1）2.34，2.44；66（2）0.315，0.355；尝33（3）(2)2，(3)2；试11练（4）1.12，0.92．习32．作出函数yx2的图象，根据图象讨论这个函数有哪些性质，并给出证明．3．作出函数yx2和函数y(x3)2的图象，求这两个函数的定义域和单调区间．4．用图象法解方程：师：引导学生回顾讨论函数性质的方法，规范解题格式与步骤．并指出函数单调性是判别大小的重要工具，幂函数的图象可以在单调性、奇偶性基础上较快描出．生：独立思考，给出解答，共同讨论、评析．师生互动设计\n（1）xx1；（2）x3x23．1．如图所示，曲线是幂函数yx在第一象限内的图象，已知分别取11,1,,2四个值，则相应2图象依次探为：．究2．在同一坐标系内，作出下列函数的图与象，你能发现什么规律？发（1）yx3和y1现x3；54（2）yx4和yx5．1．在函数作业12,yx2x,y1中，幂函数的y2,y2x回馈x个数为：A．0B．1C．2D．3环节呈现教学材料规律1：在第一象限，作直线xa(a1)，它同各幂函数图象相交，按交点从下到上的顺序，幂指数按从小到大的顺序排列．规律2：幂指数互为倒数的幂函数在第一象限内的图象关于直线yx对称．师生互动设计\n2．已知幂函数yf(x)的图象过点(2,2)，试求出这个函数的解析式．3．在固定压力差（压力差为常数）下，当气体通过圆形管道时，其流量速率R与管道半径r的四次方成正比．（1）写出函数解析式；（2）若气体在半径为3cm的管道中，流3量速率为400cm/s，求该气体通过半径为r的管道时，其流量速率R的表达式；（3）已知（2）中的气体通过的管道半径为5cm，计算该气体的流量速率．4．1992年底世界人口达到54．8亿，若人口的平均增长率为x%，2008年底世界人口数为y（亿），写出：（1）1993年底、1994年底、2000年底的世界人口数；（2）2008年底的世界人口数y与x的函数解析式．课外利用图形计算器探索一般幂函数yx活的图象随的变化规律．动收1．谈谈五个基本幂函数的定义域与对应获幂函数的奇偶性、单调性之间的关系？与2．幂函数与指数函数的不同点主要表现体在哪些方面？会