关于圆的初中数学竞赛题选 4页

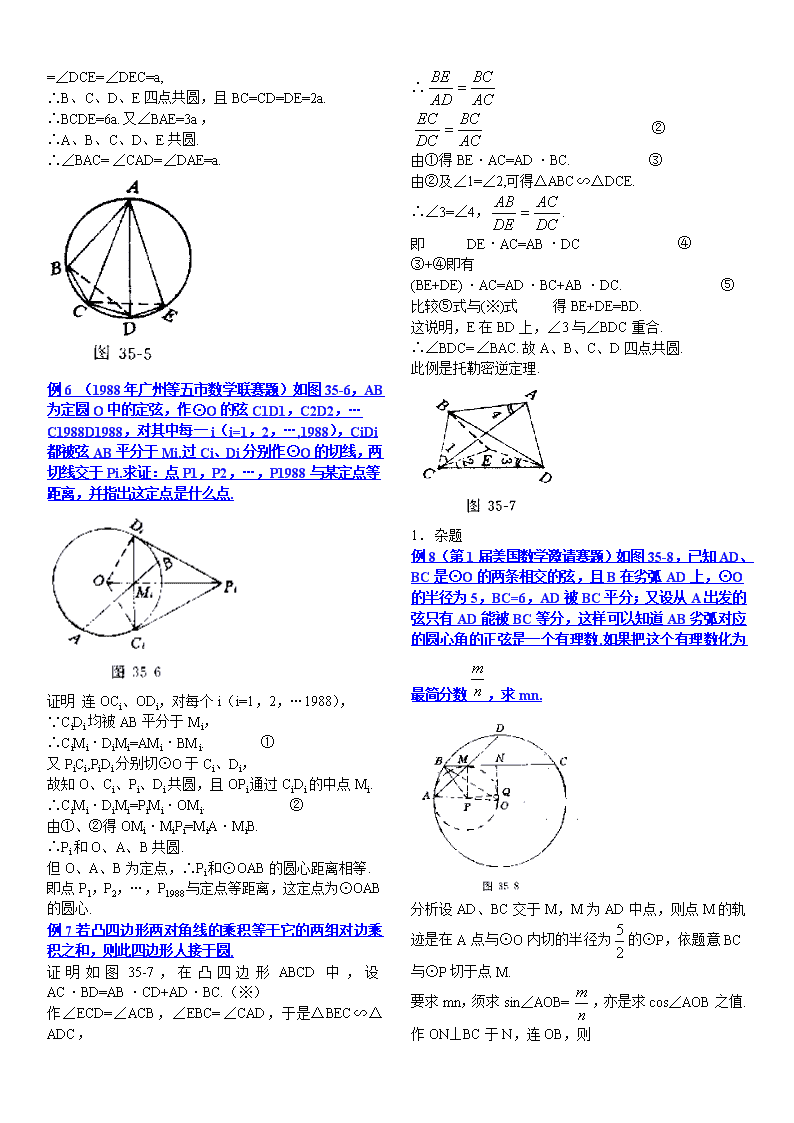
关于圆的问题 圆的有关问题是与直线型紧密结合在一起的，因而综合性强，富于变化. 圆的有关计算与证明 例1圆内接八边形的四条边长为1，另四条边长为2.求此八边形的面积. 例2在边长为1cm的正五边形,去掉所有与五边形各顶点距离都小于1cm的点,求余下部分的面积. 例3三个全等的圆有一个公共点O，并且都在一个已知△ABC内.每个圆与△ABC的两边相切.求证：△ABC的内心、外心和O点共线. 例4如图35-4，在△ABC中，BD、CE为高，F、G分别为ED、BC的中点，O为外心，求证：AO∥FG. 例5已知在凸五边形ABCDE中，∠BAE=3a,BC=CD=DE，且∠BCO=∠CDE=180°-2a，求证：∠BAC=∠CAD=∠DAE. 例6如图35-6，AB为定圆O中的定弦，作⊙O的弦C1D1，C2D2，…C1988D1988，对其中每一i（i=1，2，…,1988），CiDi都被弦AB平分于Mi.过Ci、Di分别作⊙O的切线，两切线交于Pi.求证：点P1，P2，…，P1988与某定点等距离，并指出这定点是什么点. 例7若凸四边形两对角线的乘积等于它的两组对边乘积之和，则此四边形内接于圆.托勒密逆定理例8如图35-8，已知AD、BC是⊙O的两条相交的弦，且B在劣弧AD上，⊙O的半径为5，BC=6，AD被BC平分；又设从A出发的弦只有AD能被BC等分，这样可以知道AB劣弧对应的圆心角的正弦是一个有理数.如果把这个有理数化为最简分数，求mn.例9(1962年北京中学生数学竞赛题)任意剪六个圆形纸片放在桌面上,使得没有一个纸片的中心落在另一纸片上或被另一纸片盖住,然后用一枚针去世扎这一堆纸片.证明:不论针尖落在哪一点,总是不能一次把六个纸片全部扎中.例10（第21届国际中学生数学竞赛题）如图35-10，平面上两圆相交，其中一交点为A.两动点各以匀速自A点出发在不同的圆周上同向移动，这两点移动一周后同时返回到A点.求证平面上有一定点P，它不论在何时皆和两动点等距离.\n关于圆的问题 例1（第3届全国部分省市初中数学通讯赛试题）圆内接八边形的四条边长为1，另四条边长为2.求此八边形的面积. 解由弓形面积公式知所求的八边形的面积与八边形各边排列的顺序无关. 不妨设八边形ABCDEFGH如图35-1，且有 AB=CD=EF=GH=2， BC=DE=FG=HA=1. 双向延长AH、BC、DE、FG得正方形KLMN. 故S八边形ABCDEFGH=S正方形KLMN-4S△ABK = 例2（第19届全苏中学生竞赛题）在边长为1cm的正五边形,去掉所有与五边形各顶点距离都小于1cm的点,求余下部分的面积. 解以A为圆心,1cm长为半径的扇形ABE内的点到点A的距离都小于1cm.分别以正五边形的各顶点为圆心,1cm长为半径作弧,以五段圆弧为边界的“曲边五边形”MNPQR内的点到正五边形ABCDE各顶点的距离小于1cm.五边形内余下的部分是五个等积的“曲边三角形”BMC、CND、DPE、EQA、ARB（如图35-2）. 考察“曲边三角形”BMC与以∠BAM为圆心角(等于60°)的扇形BAM的面积之和,恰等于等边三角形ABM与以∠CBM为圆心角（等于108°-60°=48°）的扇形CBM的面积之和. 所以，所要求的面积为： 5S曲边△BMC =5(S△ABM+S扇形CBM-S扇形BAM) =5= 例3（第22届国际数学竞赛题）三个全等的圆有一个公共点O，并且都在一个已知△ABC内.每个圆与△ABC的两边相切.求证：△ABC的内心、外心和O点共线. 证明如图35-3,设三等圆为⊙A′、⊙B′和⊙C′.故A′B′∥AB，B′C′∥BC，C′A′∥CA.于是△A′B′C′∽△ABC. 由于三等圆分别与△ABC的两边相切，故AA′、BB′、CC′相交于△ABC内心I.显然，I也是△A′B′C′的内心.因此，△ABC的外心E，△A′B′C′的外心E′与I三点共线. 又O是三等圆的公共点，OA′=OB′=OC′，因此O即是△A′B′C′的外心E′.故E，O、I三点共线. 四点共圆 例4（1980年哈尔滨初中数学竞赛题）如图35-4，在△ABC中，BD、CE为高，F、G分别为ED、BC的中点，O为外心，求证：AO∥FG. 证明过A作⊙O的切线AT. ∵BD、CE为高， ∴B、C、D、E四点共圆.∴∠TAC=∠ABC=∠ADE ∴AT∥ED.又AO⊥AT，∴AO⊥ED. 又∵G为BC中点，∴DG=BC=EG. 而EF=DF，∴FG⊥ED.故AO∥FG. 例5（1990年全国初中数学竞赛题）已知在凸五边形ABCDE中，∠BAE=3a,BC=CD=DE，且∠BCO=∠CDE=180°-2a，求证：∠BAC=∠CAD=∠DAE. 证明连结BD、CE. ∵BC=CD=DE， ∠BCD=∠CDE， ∴△BCD≌△CDE. 又∠BCD=180°-2a, ∴∠CBD=∠\nCDB =∠DCE=∠DEC=a, ∴B、C、D、E四点共圆，且BC=CD=DE=2a. ∴BCDE=6a.又∠BAE=3a， ∴A、B、C、D、E共圆. ∴∠BAC=∠CAD=∠DAE=a. 例6（1988年广州等五市数学联赛题）如图35-6，AB为定圆O中的定弦，作⊙O的弦C1D1，C2D2，…C1988D1988，对其中每一i（i=1，2，…,1988），CiDi都被弦AB平分于Mi.过Ci、Di分别作⊙O的切线，两切线交于Pi.求证：点P1，P2，…，P1988与某定点等距离，并指出这定点是什么点. 证明连OCi、ODi，对每个i（i=1，2，…1988）， ∵CiDi均被AB平分于Mi， ∴CiMi·DiMi=AMi·BMi.① 又PiCi,PiDi分别切⊙O于Ci、Di， 故知O、Ci、Pi、Di共圆，且OPi通过CiDi的中点Mi. ∴CiMi·DiMi=PiMi·OMi.②由①、②得OMi·MiPi=MiA·MiB.∴Pi和O、A、B共圆.但O、A、B为定点，∴Pi和⊙OAB的圆心距离相等.即点P1，P2，…，P1988与定点等距离，这定点为⊙OAB的圆心.例7若凸四边形两对角线的乘积等于它的两组对边乘积之和，则此四边形人接于圆.证明如图35-7，在凸四边形ABCD中，设AC·BD=AB·CD+AD·BC.（※）作∠ECD=∠ACB，∠EBC=∠CAD，于是△BEC∽△ADC，∴　　②由①得BE·AC=AD·BC.③由②及∠1=∠2,可得△ABC∽△DCE.∴∠3=∠4，即DE·AC=AB·DC④③+④即有(BE+DE)·AC=AD·BC+AB·DC.⑤比较⑤式与(※)式得BE+DE=BD.这说明，E在BD上，∠3与∠BDC重合.∴∠BDC=∠BAC.故A、B、C、D四点共圆.此例是托勒密逆定理.1．杂题例8（第1届美国数学邀请赛题）如图35-8，已知AD、BC是⊙O的两条相交的弦，且B在劣弧AD上，⊙O的半径为5，BC=6，AD被BC平分；又设从A出发的弦只有AD能被BC等分，这样可以知道AB劣弧对应的圆心角的正弦是一个有理数.如果把这个有理数化为最简分数，求mn.分析设AD、BC交于M，M为AD中点，则点M的轨迹是在A点与⊙O内切的半径为的⊙P，依题意BC与⊙P切于点M.要求mn，须求sin∠AOB=，亦是求cos∠AOB之值.作ON⊥BC于N，连OB，则\nBN==3，ON=作PQ⊥ON于Q,连PM,则PQNM为矩形,故有QN=PM=OP=AO=,OQ=ON-QN=MN=PQ=BM=BN-MN=1BP=在△POB中,由余弦定理,cos∠AOB===,∴sin∠AOB==∴mn=7×25=175.例9(1962年北京中学生数学竞赛题)任意剪六个圆形纸片放在桌面上,使得没有一个纸片的中心落在另一纸片上或被另一纸片盖住,然后用一枚针去世扎这一堆纸片.证明:不论针尖落在哪一点,总是不能一次把六个纸片全部扎中.分析这命题等价于：平面上有六个圆，每个圆心都在其余各圆的外部，证明平面上任意一点都不会同时在这六个圆内部.证明（反证法）如图35-9，设平面上有一点M同时在这六个圆内部，连结六个圆心：MO1，MO2，…，MO6.则∠O1MO2+∠O2MO3+…+∠O6MO1=360°.因此，至少有一个角不大于60°，不妨设∠O1MO2≤60°，即γ≤60°.又，α+β+γ=180°则α,β中必有一个不小于60°.不妨设β≥60°，则β≥γ.∴O1O2≤O1M＜r1(r1为圆⊙O1的半径).故O2在⊙O1内，这与题设矛盾，这就证明了M点不可能同时在六个圆的内部.例10（第21届国际中学生数学竞赛题）如图35-10，平面上两圆相交，其中一交点为A.两动点各以匀速自A点出发在不同的圆周上同向移动，这两点移动一周后同时返回到A点.求证平面上有一定点P，它不论在何时皆和两动点等距离.解设⊙O1与⊙O2相交于A和A′并设两动点Q1和Q2分别在⊙O1和⊙O2上，使∠AO1Q1=∠AO2Q2.连Q1A′Q2A′.因为圆周角等于同弧所对圆心角的一半，故∠AA′Q1=∠AO1Q1,∠AA′Q2=π-∠AXQ2=π-∠AO2Q2.∴∠AA′Q1+∠AA′Q2=π.即有Q1、B、Q2三点共线.过A点作MN⊥AA′分别交两圆于M、N，（如图35-11），设Q1和Q2表示两动点在任一时刻的位置.由圆内接四边形两对角互补可知∠MQ1A′=∠A′Q2N=作Q1Q的中垂线，交MN于它的中点P，点P就是所求的定点.它显然和Q1，Q2等距离.后记;