初中数学几何与面积法综合应用竞赛题精选 17页

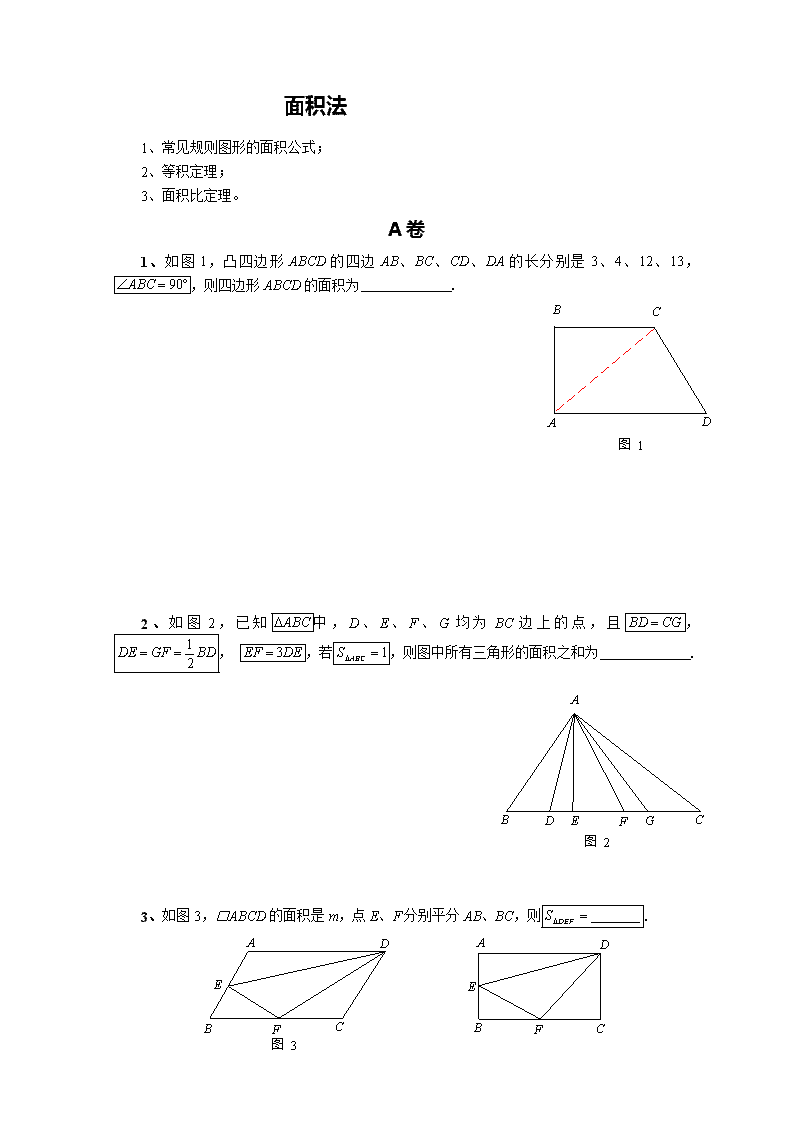
面积法1、常见规则图形的面积公式；2、等积定理；3、面积比定理。A卷1、如图1，凸四边形ABCD的四边AB、BC、CD、DA的长分别是3、4、12、13，，则四边形ABCD的面积为.图1ACBD2、如图2，已知中，D、E、F、G均为BC边上的点，且，，，若，则图中所有三角形的面积之和为.FGE图2ACBDFE图3ACBDECFABD3、如图3，□ABCD的面积是m，点E、F分别平分AB、BC，则.\n4、如图4，已知边长为a的正方形ABCD，E为AD的中点，P为CE的中点，那么的面积的值是.GFPE图4ACBD5、如图5，四边形ABCD的对角线AC和BD相交于O点，如果，，，那么.O图5ACBD\n6、（第5届“希望杯”邀请赛题）在的三边AB、BC、CA上，分别取AD、BE、CF，使，，，则的面积是的面积的（）A、B、C、D、FECABD7、（2004年第15届“希望杯”初二年级竞赛题）如图6，在直角扇形ABC内，分别以AB和AC为直径作半圆，两条半圆弧相交于点D，整个图形被分成S1，S2，S3，S4四部分，则S2和S4的大小关系是（）A、B、C、D、无法确定S2图6ACBS1S4S3\n8、在矩形ABCD中，，，则矩形的内接三角形的面积总比数的（）小或相等。A、B、C、D、B卷9、（第11届“希望杯”邀请赛）在正方形ABCD中，，点E、F分别在BC、CD上，且，，则的面积为.\nGFCDE图11AB10、（2005年第16届“希望杯”初二年级竞赛题）已知三条高的比是，且三条边的长均为整数，则的一条边长可能是（）A、10B、12C、14D、1611、（第14届“希望杯“邀请赛）如图7，将的三边AB，BC，CA分别延长至，，，且使，，，若，那么是（）A、15B、16C、17D、18C′A′B′A图7CB\nDGEFA图8CB12、（2005年第16届“希望杯”初二年级竞赛题）如图8，中，，四边形BDEC和ACFG分均为正方形，已知与正方形BDEC的面积比是，那么与整个图形的面积比等于.C卷13、（第6届“希望杯“邀请赛题）如图9，的面积为，点D、E、F分别位于AB、BC、CA上，且，，如果的面积和四边形DBEF的面积相等，则的面积是（）\nA、B、C、D、FEDCA图9B14、（第7届“希望杯“邀请赛题）如图10，直角内有一点P，，，过点P作一直线MN与OA、OB分别交于M、N，使的面积最小。PNMOA图10BNPMOA图11B\n（1）此时线段MN的位置是（）A、B、C、D、（2）此时的面积是.（3）若为一锐角，P是锐角内一定点（如图11），过点P的直线与OA、OB交于M、N，使的面积最小。应怎样画出MN的位置，并证明你的结论。面积法\n1、常见规则图形的面积公式；2、等积定理；3、面积比定理。A卷1、如图1，凸四边形ABCD的四边AB、BC、CD、DA的长分别是3、4、12、13，，则四边形ABCD的面积为.答案：36考点：勾股定理；勾股定理的逆定理。分析：连接AC，在中，已知AB、BC根据勾股定理可以求得，在中，，根据勾股定理的逆定理确定为直角三角形，四边形ABCD的面积为和面积之和。图1ACBD解答：连接AC，在中，，，则又∵∴为直角三角形∴的面积为，的面积为∴四边形ABCD的面积为和面积之和，故答案为36．点评：本题考查了勾股定理在直角三角形中的运用，考查了直角三角形面积的计算，本题中判定为直角三角形是解题的关键。2、如图2，已知中，D、E、F、G均为BC边上的点，且，，，若，则图中所有三角形的面积之和为.答案：7考点：三角形面积与底的正比关系。分析：如图所示的所有三角形都具有相等的高，于是可将计算所有三角形面积之和的问题转化为计算BC上所有线段长度之和的问题。FGE图2ACBD解答：因为所有线段长之和是BC的n倍∴图中所有三角形面积之和就是的n倍设，则，，∴图中共有个三角形则它们在线段BC上的底边之和为：\n由此可知BC上所有线段之和63是BC=9的7倍∴图中所有三角形面积之和等于的7倍．已知，故图中所有三角形的面积之和为7．故答案为：7点评：此题主要考查学生对三角形面积的理解和掌握，解答此题的关键是图中所有三角形都具有相等的高，通过转化的思想，找出解决问题的捷径。FE图3ACBDECFABD3、如图3，□ABCD的面积是m，点E、F分别平分AB、BC，则.答案：解答：不妨设□ABCD为长方形，如图，则有，∴4、如图4，已知边长为a的正方形ABCD，E为AD的中点，P为CE的中点，那么的面积的值是.答案：考点：正方形的性质；三角形的面积；勾股定理。分析：观察图形可以发现，所以要求的面积分别计算、、、即可。解答：过P作，，则，，GFPE图4ACBD观察图形可以发现∴∴点评：本题考查了正方形各边长相等、各内角为直角的性质，考查了三角形面积的计算，本题中正确计算、、、是解题的关键。5、如图5，四边形ABCD的对角线AC和BD相交于O点，如果，，\n，那么.答案：考点：三角形的面积。分析：先设出一个三角形的面积：的面积是，再用代数式表示出图中其它三角形的面积，利用中间桥得出方程，进一步求出结果。解答：设的面积是，则的面积是，的面积是，的面积是O图5ACBD∵的边OA上和的边上的高相等∴，同理∴即，解得：∴点评：解此题的关键是灵活运用三角形的面积公式，等高时面积比等于边之比，从而转化成解方程，求出未知数的值。6、（第5届“希望杯”邀请赛题）在的三边AB、BC、CA上，分别取AD、BE、CF，使，，，则的面积是的面积的（）A、B、C、D、答案：A考点：三角形的面积。分析：连接AE．根据三角形的面积公式求得和的面积比，和的面积比，进而求得和的面积比，同理求得、和的面积比，最后求解。解答：如图，连接AEFECABD∵，∴，∴同理可得：，\n所以点评：此题考查了根据三角形的面积公式求三角形的面积比的方法。7、（2004年第15届“希望杯”初二年级竞赛题）如图6，在直角扇形ABC内，分别以AB和AC为直径作半圆，两条半圆弧相交于点D，整个图形被分成S1，S2，S3，S4四部分，则S2和S4的大小关系是（）A、B、C、D、无法确定答案：B考点：扇形面积的计算。分析：设，由S2=S，根据扇形和圆的面积公式分别计算出它们的面积就可得到和的大小关系。S2图6ACBS1S4S3解答：设，根据题意得：故故选B．点评：本题考查了扇形的面积公式：，其中n为扇形的圆心角的度数，R为圆的半径），或，为扇形的弧长，R为半径。8、在矩形ABCD中，，，则矩形的内接三角形的面积总比数（）小或相等。A、B、C、D、答案：B解答：需分类讨论，如图，显然图（甲）及图（乙）中内接三角形面积为1，如图（丙）、（丁）、（戊）中的面积显然小于1，综上所述，故选B.甲DACBE乙DACBEGF丙DACBEGF丁DACBEGF戊DACBE\nB卷9、（第11届“希望杯”邀请赛）在正方形ABCD中，，点E、F分别在BC、CD上，且，，则的面积为.答案：考点：正方形的性质；全等三角形的判定与性质；旋转的性质。分析：将绕A点顺时针方向旋转90°到的位置，得到，得，要求的面积求即可，且AB为底边上的高，EG为底边。解答：将绕A点顺时针方向旋转90°到的位置GFCDE图11AB∴，，，∴又∴∴，在中，，∴，在中，，，∴，∴点评：本题考查了全等三角形的证明，考查了正方形各边各内角均相等的性质，解本题的关键是巧妙地构建，并且求证．10、（2005年第16届“希望杯”初二年级竞赛题）已知三条高的比是，且三条边的长均为整数，则的一条边长可能是（）A、10B、12C、14D、16答案：B考点：约数与倍数；三角形的面积。专题：推理填空题。分析：根据题意，设三边为X，Y，Z，运用三角形面积公式得到，据给出的已知条件得出三边之比，既而得出答案。解答：解：设三边为X，Y，Z三条对应的高为，，可得：\n已知可得因为三边均为整数又4个答案分别是10，12，14，16所以答案应该是12故选B．点评：此题考查了学生对公倍数和三角形面积的理解和掌握。关键是运用三角形面积公式得到，据给出的已知条件得出三边之比。11、（第14届“希望杯“邀请赛）如图7，将的三边AB，BC，CA分别延长至，，，且使，，，若，那么是（）A、15B、16C、17D、18答案：D考点：三角形的面积。专题：计算题。分析：连接，利用，，．若，求得，同理可求得和，然后即可得出答案。C′A′B′A图7CB解答：连接∵∴又∴∴同理可得，∴∴故选D．点评：此题主要考查学生对三角形面积的理解和掌握，解答此题的关键是连接，求得.12、（2005年第16届“希望杯”初二年级竞赛题）如图8，中，，四边形BDEC和ACFG分均为正方形，已知与正方形BDEC的面积比是，那么与整个图形的面积比等于.答案：考点：相似三角形的判定与性质。专题：计算题。\n分析：根据三角形面积计算公式即可求得和的面积相等，设，则即可计算的面积和整个图形的面积，即可求得与整个图形的面积比，即可解题。解答：∵，，DGEFA图8CB∴和的面积相等设则正方形BDEC的面积为9，四边形BDEC的面积为25的面积为故整个图形的面积比为∴与整个图形的面积比点评：本题考查了三角形面积的计算，锐角和其补角的正弦值相等的性质，正方形面积的计算，本题中求和整个图形的面积是解题的关键。C卷13、（第6届“希望杯“邀请赛题）如图9，的面积为，点D、E、F分别位于AB、BC、CA上，且，，如果的面积和四边形DBEF的面积相等，则的面积是（）A、B、C、D、答案：C考点：三角形的面积。专题：转化思想。分析：本题由题意可知的面积和四边形DBEF的面积相等，可通过连接DE，DC的方法，证明出，进而求出的面积，然后即可求出答案。解答：连接DE，DC∵FEDCA图9B∴∵两个三角形有公共底DE，且面积相等∴高相等∴从而可得：S∴又，∴\n即点评：本题考查三角形面积性质的应用，可通过作辅助线的方法，做此题时注意理清各个三角形面积之间的关系。14、（第7届“希望杯“邀请赛题）如图10，直角内有一点P，，，过点P作一直线MN与OA、OB分别交于M、N，使的面积最小。PNMOA图10BNPMOA图11B（1）此时线段MN的位置是（）A、B、C、D、（2）此时的面积是.（3）若为一锐角，P是锐角内一定点（如图11），过点P的直线与OA、OB交于M、N，使的面积最小。应怎样画出MN的位置，并证明你的结论。解：（1）如图（甲），当时，的面积最小，理由同第（3）小题。（2）由（1）可知，当时，的面积最小∵是直角三角形FGECOPMN乙ABOPMN甲AB∴∴又∵∴∴，∴丙F′E′G′OPMNAB（3）作法1，如图（乙）①过P点交OB于C；②在OB上截取；③连结NP并延长交OA于M.则MN即为所求线段，此时\n∵，∴∴的面积最小证明：若经过点F另有一条直线EF交OA、OB于E、F，MN作交EF于G，可证明∴∴若过点交OA、OB于、（如图丙），则作交于，同理可证∴是符合要求的面积最小的三角形。