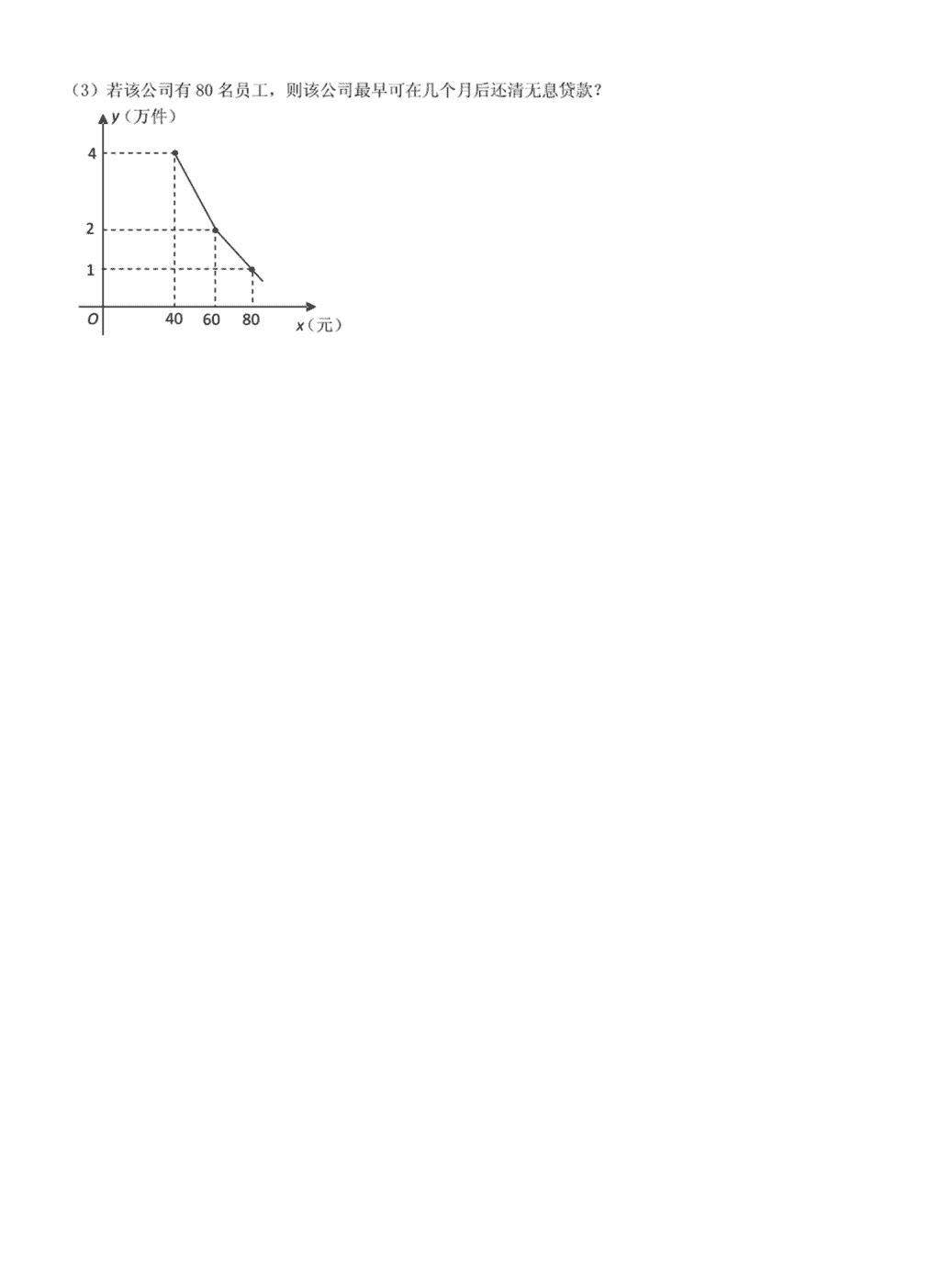初中数学压轴练习3 13页

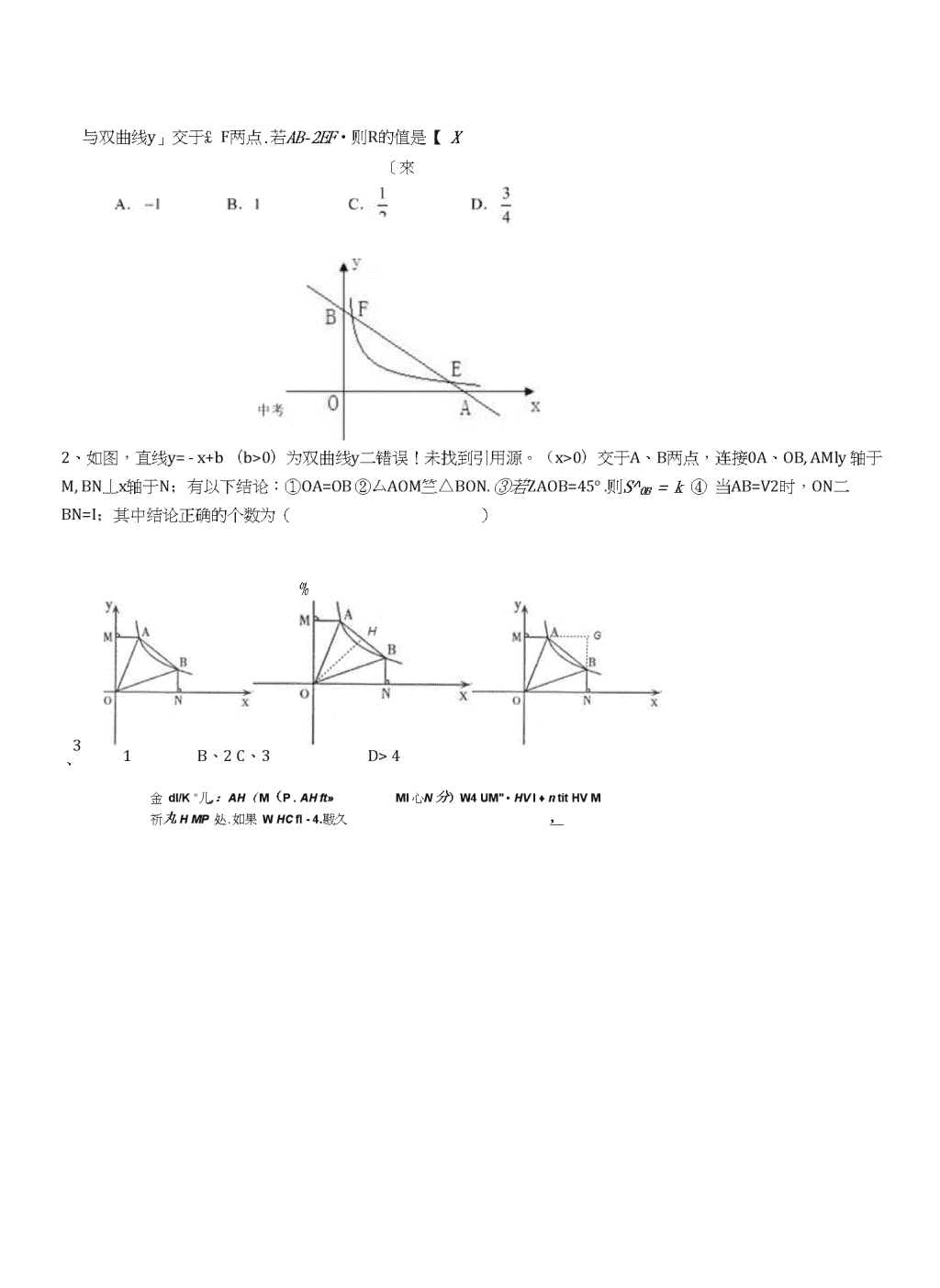
与双曲线y」交于£F两点.若AB-2EF•则R的值是【X［來2、如图，直线y=-x+b（b>0）为双曲线y二错误！未找到引用源。（x>0）交于A、B两点，连接0A、OB,AMly轴于M,BN丄x轴于N；有以下结论：①OA=OB②厶AOM竺△BON.③若ZAOB=45°.则S^0B=k④当AB=V2时，ON二BN=I；其中结论正确的个数为（）%1B、2C、3D>4金dl/K"儿,：AH（M（P.AHft»Ml心N分）W4UM"•HVI♦ntitHVM祈丸HMP处.如果WHCfl-4.戡久，3、\n4、如图.在菱形ABCD'\\AB^l.Z048=60°.把菱形AMD绕点4顺时什旋转30”得刘菱形莫中点C的运动路径为CC',则图屮阴谄部DC分的而积为一.・5、为了扶持大学生自主创业，市政府提供了80万元无息贷款，用于某大学生开办公司生产并销售自主研发的一种电子产品，并约定卅该公司经营的利润逐步偿还无息贷款.已知该产品的牛产成本为每件40元，员工每人每月的工资为2500元，公司每月需支付其它费用15万元•该产品每月销售量y（万件）与销售单价兀（元）之间的函数关系如图所示.（1）求月销售量y（万件）与销售单价x（元）之间的函数关系式；（2）当销售单价定为50元时，为保证公司月利润达到5万元（利润=销售额一生产成本一员工工资一其它费用），该公司可安排员工多少人？\n\n6、如图，的半径为1,点P是00±一点，弦AB垂直平分线段0P,点D是APB上任一点（与端点A、B不重合），DE丄AB于点E,以点D为圆心、DE长为半径作OD,分别过点A、B作OD的切线，两条切线相交于点C.（1）求弦AB的长；（2）判断ZACB是否为定值，若是，求出ZACB的大小；否则，请说明理由；（3）记Z\ABC的面积为S,若壬=4爲,°求AABC的周长.7、在四边形ABCD中，対角线AC、和交于点0,设锐角ZD0C=a,将ADOC绕点0按逆时针方向旋转得到△D’OC'（0°<旋转角<90°）,连接AC’、BD，,AC'与BD'相交于点M.（1）当四边形ABCD是矩形时，如图1,请猜想AC'与BD‘的数量关系以及ZAMB与a的人小关系，并证明你的猜想；（2）当四边形&BCD是平行四边形时，如图2,已知AC=kBD,请猜想此时4C，与BD'的数量关系以及ZAMB与Q的大小关系，并证明你的猜想；（3）当四边形&BCD是等腰梯形时，如图3,AD//BC,此吋（1）AC'与BD'的数量关系是否成立？ZAMB与a的人小关系是否成立？不必证明，肓接写出结论.\nCfD图1图2图3\n8、在平面直角坐标系xOy中，已失哋物线尸久乂+l)'+u(a>0)与*轴交于A.B两点(点A在点B的左侧)，与y轴交于点C,其顶点为儿若戟版的函数表达式为y^kx-3,与X轴的交点为N,且COSZB：O=^2o10(1)求此抛物线的函数表达式；⑵在此抛物线上是否存在异干点C的点P,使以N、P、C为顶点的三角形是以N：为一条直角边的直角三角形？若存在，求出点P的坐标：若不存在，请说明理曲(3)过点A作x轴的垂线，交直线MC于点Q.若将抛物线?吕其对称庁由上下平移，使抛物线与线段N3总有公共点，则抛物线向上最多可平移多少个单位长度？向下最多可平移多少个单位长度？故选D・\n2、D考点：反比例函数综合题。专题：计算题。分析：①②设A（xi，yi）,B（X2，丫2），联立y=-x+bA/y=错误！未找到引用源。，得x2-bx+k=O,则xi*x2=k,又xi*yi=k,比较可知x2=yi，同理可得Xi=y2，即ON=OM,AM=BN,nJ*证结论；③作OH丄AB,垂足为H,根据对称性可证△OAM今△OAHMZ\OBH/AOBN,可证SAAOB=k;④延长MA,NB交于G点，可证AABG为等腰直角三角形，当AB二错误！未找到引用源。时，GA=GB=1,则ON-BN=GN-BN=GB=1；解答:解：设A（xi，yi）,B（X2,丫2），代入y二错误！未找到引用源。中，得xi*yi=x2ey2=k,联立错误！未找到引用源。，得x2-bx+k=O,则xi»x2=k,又xi*yi=k,.*.X2=yi，同理可得xi=y2,AON=OM,AM=BN,・••①0A二0B,②△AOM$Z\BON,正确；③作OH丄AB,垂足为H,VOA=OB,ZAOB=45°,二△OAM竺△OAH竺△OBH竺△OBN,•'•Saaob=Saaoh+Saboh=Saaom+Sabon=错误！未找到引用源。k+错误！未找到引用源。k=k,正确；④延长MA,NB交于G点，・.・NG=OM=ON=MG,BN=AM,AGB=GA,AAABG为等腰总角三角形，当AB二错误！未找到引用源。时,GA=GB=1,AON-BN=GN-BN=GB=1,正确.正确的结论有4个.故选D.3、HPFHP傀^1*1?11a尸・fill尸〃•JFMti刖哼44/IV//•叽NNHw乙WHHitl\H4、5、解：(1)当40WxW6CI时，令y=kx+b,40Jt+b=46Qk^b=29方=8解得故y=<故尸-挣十8,同理，当时，〉=-寻c乜-^x+8(40|3,/.ZAOP=60AZAOB=120°,・・•点D为△ABC的内心，/.ZCAB=2ZDAE,ZCBA=2ZDBA,VZDAE+ZDBA=^ZAOD+^-ZDOB=^-ZAOB=60222/.ZCAB+ZCBA=120D,AZACB=60°.\n(3)15AABC的周长为1,取AC,BC与OD的切点分别为G,H,连接0D・连接DG,DC,DH,贝i］有DG二DH二DE,DG丄AC,DH1BC,・•・s=saabd+saacd+sabcd=|aB・DE+£eC・DH+£aC・DG丄(AB+BC+AC)・DE=Z1・DE,DE£・•・1=8也DE,・・・CG,CH是OD的切线,AZGCD=-ZACB=30"・・・CH二CG二也DE,又由切线长定理可知AG二AE,BH=BE,・•・AG+BH=AE+BE=AB,・・・1二AB+BC+AC二AB+AG+BH+CG+CH=2(AB+CG)=2苗+2A*DE=8^DE,解得DE斗・•・AABC的周长为芈.3\n解：mAC'=BD;,ZAMB=a,/.OA=OC=OB=OD,又VOD=OD/,OC=OC/,/.OB=OD?=OA=OC,,VZD?OD二ZC'OC,・•・180°-ZD'OD=180°-ZC?OC,AZBOD?=ZA0C/,・•・△BOD'AA0C/,/.BD/二AC',/.ZOBD?=Z0AC?,设与OA相交干点N,/.ZBN0=ZANM,・•・180°-ZOAC/-ZANM=180°-ZOBD?-ZBNO,即ZAMB=ZAOB=ZCOD=a,综上所述，BDZ=AC?,ZAMB=a,DrDrd‘\n(1)AC'=kBDz,ZAMB=a,证明;•・•在平行四边形ABCD中,OB=OD,OA=OC,又VOD=OD/,OC二0C‘,・・・0C‘=0A,0D?=0B,VZD;0D=ZC;OC,・・・180°-ZD'0D=180o-ZCZOC,/.ZBOD;=ZA0C;,・・・△BOD's^AOC',/.BD;:AC'=OB：OA=BD：AC,•・•AC=kBD,AC;=kBD;,•••△BOD's^AOC',设BU与OA相交于点N,・・・ZBNO=ZANM,・・・180°一ZOAC'-ZANM=180°-ZOBD;-ZBNO,即ZAMB=ZAOB=a,综上所述，ACZ=kBDz,ZAMB=a,(2)ACZ=BDZ成立，ZAMB二a不成立.2&解：(1)•••臓MC的函数表达式为y%・3..•.点C(0・-3).……1分.・.可设|处|=3心＞0),1肚！则由勾股定理•紛OHI"而|必|=3(=3./.:=1,r.点欣1.0)..・.拋物线的函数农达式为厂(“1)—*4-3.……】分•・•点輿,0)^(0,-3)在拋物线上,\n（2）假设在抛物线上存在异于点C的点P,使以N、P、C为顶点的三角形是以NC为一条直角边的宜角三角形.①为另一条直角边.•••点M（4）在直线上，.•・-4=-—3,即"I.•・.直线MC的函数表达式为yp-3.易得玄线MC与x轴的交点N的坐标为"（3,0）.・•\OC\=|OV|・・・.厶CNO=45：在y轴上取点"（0,3）,连结ND交抛物线于点P.•/|OiV|=|OP|t.\乙DNO75：・•・厶PNC=90：设宜统ND的函致表达式为）二砂+从3m+n=0.m=-1»由ans3n^3.・•.直线N〃的議数表达式为）工-x+3.设点P（.d3）•代入抛物线的函数表达式•得-r+3=x2•*2x-3,RP+3.r-6=0.冲屮■3*v'33■3-0)个单位•可设函数表达式为厂』+2一3+6.由厂宀2一3仏消去八得宀占"ly"_3.・•要使抛物线与线段NQ总有交点，必须△=】-4b=0.即6w4~・・'・00)个单位•可设函数表达式为厂/+2x・3-6・•当"・3时』=-6；当％=3时』=12-6.易求得(?(-3.-6),又M3,0)・.••要使抛物线与线段NQ总有交点•必须-6或12・6=0,即6W6或6W12.r.0<6W12./.若拋物线向下平移•最多可平移12个敢位长度……1分［或:若抛物线沿其对称轴向下平移•设平移b(b>0)个单位.则)'t=x'+2x-3-6,j2-3在-3W%W3总有交点.即九=x3+2x-3-&-Ar+3=xa*x-6=0在■3W%W3总有实数根.令y=J4-x=(x4-+)'-—.在■3WxW3时・W12・.・.斐使d“在-3WjtW3有解上必须满足-*W6W12・・・・()<6W12.即6的Jft大值为12・・・・向下最多可平移12个单位长度.J综上可知，若将抛物线沿其对称轴上下平移•使抛物线与线段NQ总有公共点，刚向上跟多可平移扌个单位长度•向下殂多可平移12个单位长度.