初中几何点专题练习 2页

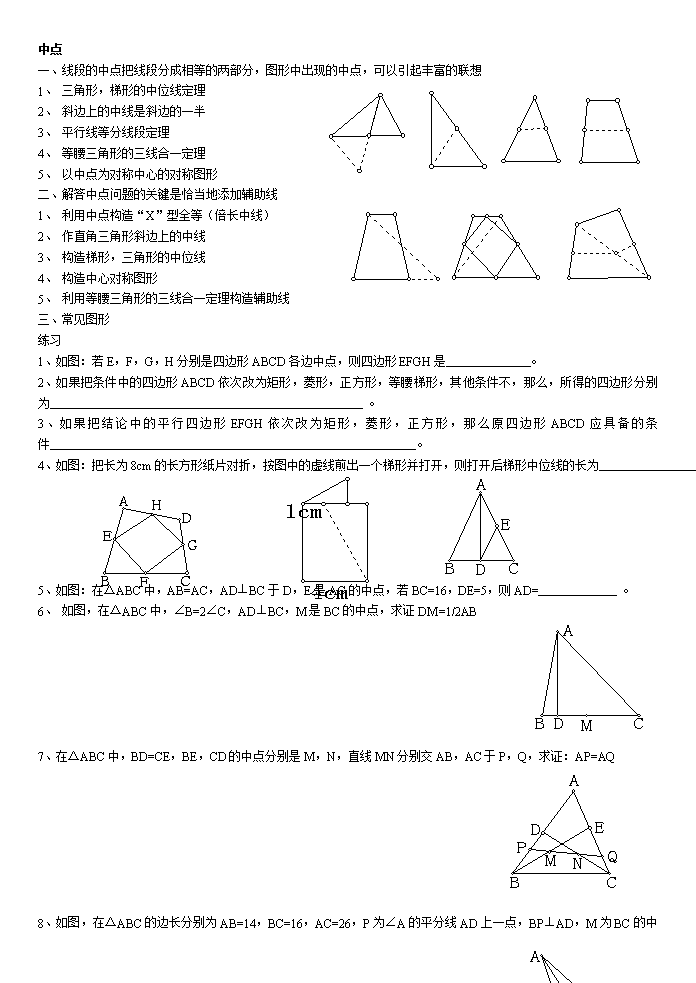
中点一、线段的中点把线段分成相等的两部分，图形中出现的中点，可以引起丰富的联想1、三角形，梯形的中位线定理2、斜边上的中线是斜边的一半3、平行线等分线段定理4、等腰三角形的三线合一定理5、以中点为对称中心的对称图形二、解答中点问题的关键是恰当地添加辅助线1、利用中点构造“X”型全等（倍长中线）2、作直角三角形斜边上的中线3、构造梯形，三角形的中位线4、构造中心对称图形5、利用等腰三角形的三线合一定理构造辅助线三、常见图形练习1、如图：若E，F，G，H分别是四边形ABCD各边中点，则四边形EFGH是。2、如果把条件中的四边形ABCD依次改为矩形，菱形，正方形，等腰梯形，其他条件不，那么，所得的四边形分别为。3、如果把结论中的平行四边形EFGH依次改为矩形，菱形，正方形，那么原四边形ABCD应具备的条件。4、如图：把长为8cm的长方形纸片对折，按图中的虚线煎出一个梯形并打开，则打开后梯形中位线的长为。5、如图：在△ABC中，AB=AC，AD⊥BC于D，E是AC的中点，若BC=16，DE=5，则AD=。6、如图，在△ABC中，∠B=2∠C，AD⊥BC，M是BC的中点，求证DM=1/2AB7、在△ABC中，BD=CE，BE，CD的中点分别是M，N，直线MN分别交AB，AC于P，Q，求证：AP=AQ8、如图，在△ABC的边长分别为AB=14，BC=16，AC=26，P为∠A的平分线AD上一点，BP⊥\nAD，M为BC的中点，求PM的值9、如图，□ABCD中，∠ABC=75°，AF⊥BC于F，AF交BD于E，若DE=2AB，求∠AED的度数10、正方形ABCD的两条对角线相交于E，∠CAD的平分线AF交DE于G，交DC于F，若GE=24，求FC的大小11、如图：在△ABC中，∠BAC=120°，以AB，AC为边分别形外作正三角形ABD，ACE，M为AD中点，N为AE中点，P为BC中点，求∠MPN12、在梯形ABCD中，AB∥CD，M为DC的中点，N为AB的中点，求证：MN<1/2（AD+BC）13、如图，△ABC的∠B的角平分线BE与BC边上的中线AD垂直且相等，已知BE=AD=4，求△ABC的三边长14、锐角三角形ABC中，作高BD，CE，过顶点B，C分别作ED的垂线BF和CG，求证：EF=DG15、在△ABC中，AD是BC边上的中线，点M在AB边上，点N在在AC边，且∠MDN=90°，如果BM2+CN2=DM2+DN2,求证：16、请选择恰当的方法将如图的梯形分割成面积相等的四块