初中数学练习题(六) 4页

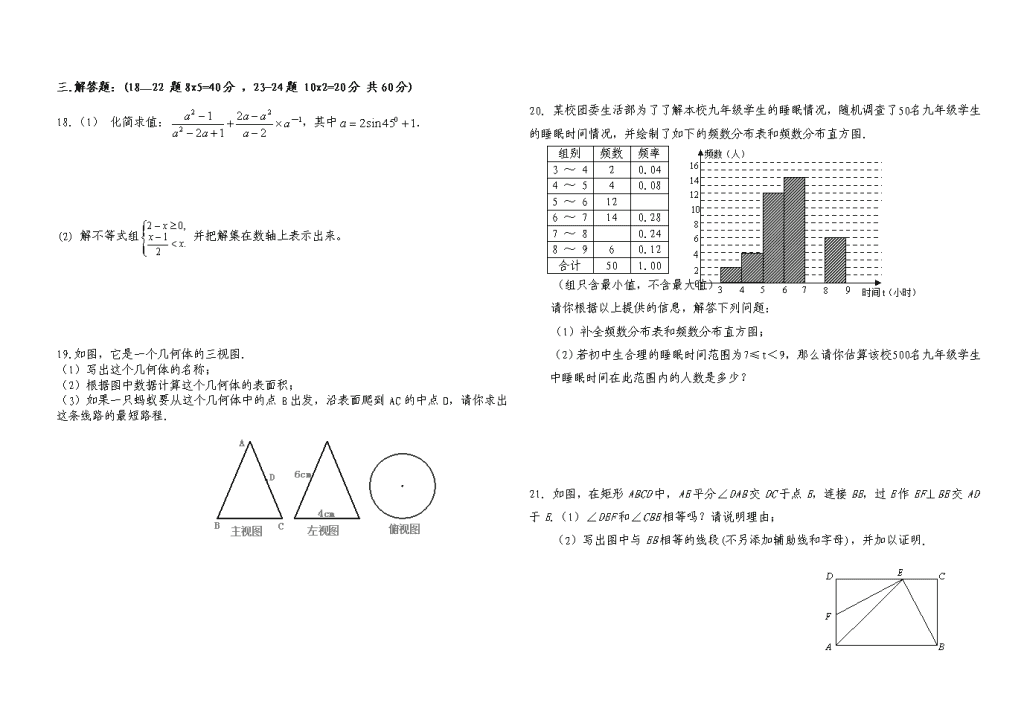
初中数学练习题（六）田庄中学一、选择题：（1—8题3x8=24分，9—12题4x4=16分共40分）1.－6的相反数的倒数是（）A.－6B.6C.D.2.温家宝总理有句名言：“多么小的问题乘以13亿，都会变得很大；多么大的经济总量，除以13亿都会变得很小”据国家计局的公布，2004年我国淡水资源总量为26520亿立方米，居世界第四位，但人均只有()立方米，是全球人均水资源最贫乏的十三个国家之一。（结果保留两位有效数字）。A.2.04×10亿立方米B.2.040×1011立方米C.2.04×108立方米D.2.04×1011立方米3.用两个完全相同的三角形不能拼成下列图形的是（）A.平行四边形B.矩形C.等腰三角形D.梯形BACD正面4.小明从正面观察下图所示的两个物体，看到的是（）5.一元二次方程的解是（）A.B.C.D.6.已知圆锥的侧面积为10πcm2，侧面展开图的圆心角为36º，则该圆锥的母线长为（）A.100cm　B.10cm　　C.cm　D.cmABCO第8题图7.某校在“校园十佳歌手”比赛上，六位评委给1号选手的评分如下：90，96，91，96，95，94.那么，这组数据的众数和中位数分别是（）A.96，94.5B.96，95C.95，94.5D.95，958.如图，AB是圆O的直径，∠C=20º，则∠BOC的度数是（）A.10ºB.20ºC.30ºD.40º9.若反比例函数y=的图象经过点（-1,2)，则这个函数的图象一定经过点（）　　A.(2,-1)　　　B.(,2)　　　C.(-2,-1)　　　D.(,2)10.已知菱形的边长为6，一个内角为60oº，则菱形内切圆的半径是（）A.3B.3：2C.3D.6ABC15°PABC15°P第11题图11.如图，将一个Rt△ABC形状的楔子从木桩的底端点P沿水平方向打入木桩底下，使木桩向上运动.已知楔子斜面的倾斜角为15°，若楔子沿水平方向前进6cm（如箭头所示），则木桩上升了（）A.6sin15°cmB.cmC.6tan15°cmD.6cos15°cm12.给出下列函数：①y=2x；②y=-2x+1；③（x>0）；④(x<-1).其中，y随x的增大而减小的函数是（）A.①②B.①③C.②④D.②③④二.填空题：（4x5=20分）13.分解因式：—=.14.抛物线的顶点关于x轴对称的点的坐标为_________.15.个矩形纸片上画出半径分别是4cm的一个圆，再画两个与它外切的、半径是1cm的外切圆，该矩形纸片面积的最小值是.16从-1，1，2这三个数中，任取两个不同的数作为一次函数y=kx+b的系数k，b，则一次函数y=kx+b的图象不经过第四象限的概率是．17如图，把一个矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连结OB，将若，，求以OB为斜边，与△OBC全等的三角形顶点D的坐标.\n三.解答题：(18—22题8x5=40分，23-24题10x2=20分共60分)18.（1）化简求值：，其中.(2)解不等式组并把解集在数轴上表示出来。19.如图，它是一个几何体的三视图.（1）写出这个几何体的名称；（2）根据图中数据计算这个几何体的表面积；（3）如果一只蚂蚁要从这个几何体中的点B出发，沿表面爬到AC的中点D，请你求出这条线路的最短路程.频数（人）时间t（小时）0242628210121416345678920.某校团委生活部为了了解本校九年级学生的睡眠情况，随机调查了50名九年级学生的睡眠时间情况，并绘制了如下的频数分布表和频数分布直方图.组别频数频率3～420.044～540.085～6126～7140.287～80.248～960.12合计501.00（组只含最小值，不含最大值）请你根据以上提供的信息，解答下列问题：（1）补全频数分布表和频数分布直方图；（2）若初中生合理的睡眠时间范围为7≤t＜9，那么请你估算该校500名九年级学生中睡眠时间在此范围内的人数是多少？21.如图，在矩形ABCD中，AE平分∠DAB交DC于点E，连接BE，过E作EF⊥BE交AD于E.（1）∠DEF和∠CBE相等吗？请说明理由；（2）写出图中与EB相等的线段(不另添加辅助线和字母)，并加以证明.ABCDEF\n22.（12分）如图，在Rt△ABC中，∠ACB＝90°，D点是AB上的一点，以BD为直径的⊙O与边AC相切于点E，连结DE并延长，与BC的延长线交于点F.（1）求证：BD＝BF；（2）当BC＝3，AD＝2时，求⊙O的面积；（3）在（2）的条件下，判断△DBF是否为正三角形?并说明你的理由.23.(本题满分10分)已知抛物线y=x2+(2n-1)x+n2-1(n为常数).(1)当该抛物线经过坐标原点，并且顶点在第四象限时，求出它所对应的函数关系式；(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点，过A作x轴的平行线，交抛物线于另一点D，再作AB⊥x轴于B，DC⊥x轴于C.①当BC=1时，求矩形ABCD的周长；②试问矩形ABCD的周长是否存在最大值？如果存在，请求出这个最大值，并指出此时A点的坐标；如果不存在，请说明理由.24.（12分）如图，在梯形ABCD中，AD∥BC,AD=2,BC＝4，点M是AD的中点，△MBC是等边三角形.（1）求证：梯形ABCD是等腰梯形；（2）动点P、Q分别在线段BC和MC上运动，且∠MPQ＝60°保持不变.设PC＝x，MQ＝y,求y与x之间的函数关系式；（3）在（2）的条件下：①当动点P、Q运动到何处时，以点P、M和点A、B、C、D中的两个点为顶点的四边形是平行四边形？并指出符合条件的平行四边形的个数；②当y取最小值时，判断△PQC的形状，并说明理由.\n