初中各类方程的解法及练习 6页

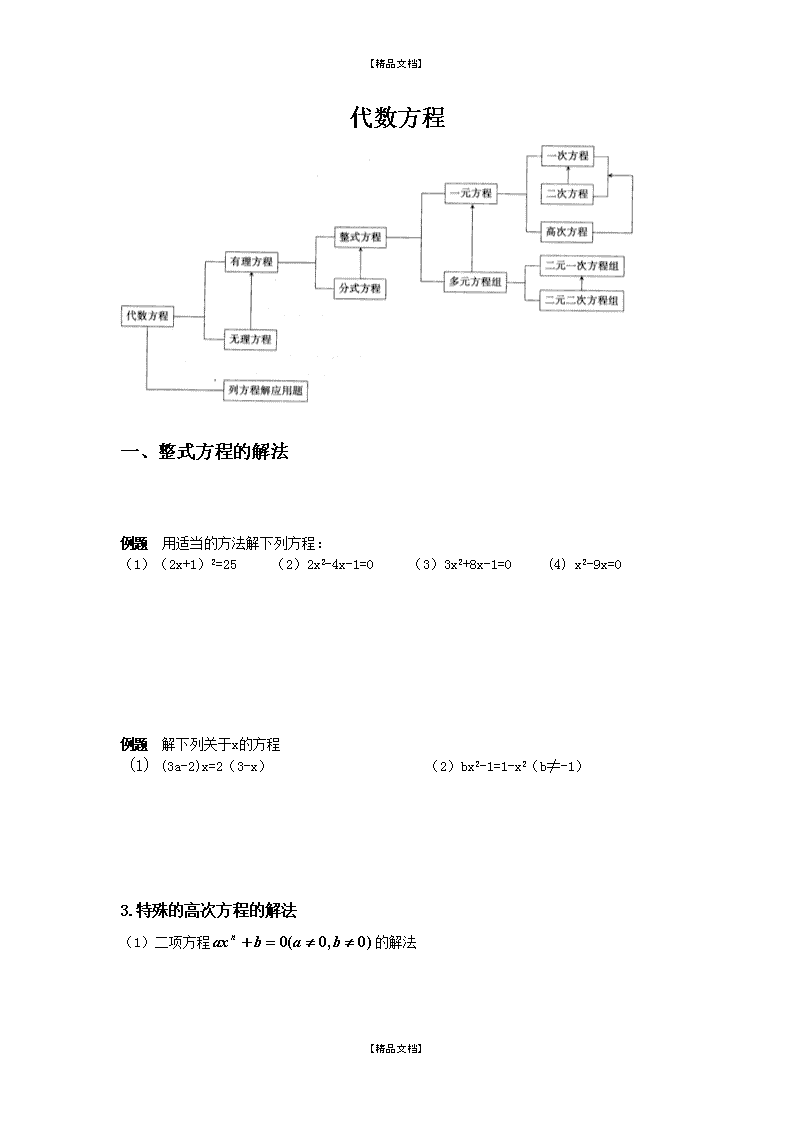
------------------------------------------作者xxxx------------------------------------------日期xxxx初中各类方程的解法及练习\n【精品文档】代数方程一、整式方程的解法例题用适当的方法解下列方程：（1）（2x+1）2=25（2）2x2-4x-1=0（3）3x2+8x-1=0(4)x2-9x=0例题解下列关于x的方程（1）(3a-2)x=2（3-x）（2）bx2-1=1-x2（b≠-1）3.特殊的高次方程的解法（1）二项方程的解法【精品文档】\n【精品文档】例题判断下列方程是不是二项方程，如果是二项方程，求出它的根。（1）x3-64=0（2）x4+x=0（3）x5=-9（4）x3+x=1（2）双二次方程的解法例题判断下列方程是不是双二次方程，如果是，求出它的根：（1）x4-9x2+14=0（2）x4+10x+25=0（3）2x4-7x3-4=0（4）x4+9x2+20=0（3）因式分解法解高次方程例题解下列方程：（1）2x3+7x2-4x=0（2）x3-2x2+x-2=04.二元二次方程组例题解下列方程组（1）（2）二、可化为一元二次方程的分式方程的解法例题解下列方程（1）【精品文档】\n【精品文档】（2）（3）三、无理方程的解法1．只有一个含未知数根式的无理方程例题解下列方程：(1)（2）例题解下列方程：（1）（2）3.适宜用换元法解的无理方程例题解方程【精品文档】\n【精品文档】代数方程练习中，若设，则原方程化为关于y的方程是.2.当m=时，关于x的分式方程没有实数解.有实数根，则a的取值范围是.时，可设=y,这时原方程变为.的根是；的根是；的根是.的根为，则a的值为.7.若a，b都是正实数，且，则.8.若a+b=1，且a∶b=2∶5,则2a-b=.9.当a=时，方程无实数根.，则.11.下列方程中既不是分式方程，也不是无理方程的有（）A.B.C.D.E.F.12．方程的最简公分母是（）A.24（x+3）(x-3)B.(x+3)(x-3)2C.24（x+3）(x-3)2D.12（x+3）(x-3)213.观察下列方程，经分析判断得知有实数根的是（）A.B.C.D.【精品文档】\n【精品文档】，那么的值是（）A.1B.-1C.±15.方程的解是（）16.A.0B.2C.0或2D.,则方程可变形为（）A.B.C.D.，则a的取值范围是（）≥0≥≤，则相等关系成立的式子是（）A.B.C．D.的根是（）A.x=aB.x=-a1=a；x2=-1=a；x2=20.一个数和它的算术平方根的4倍相等，那么这个数是（）21.；22.；23.；24.【精品文档】