初中数学《直线型面积》讲义及练习 13页

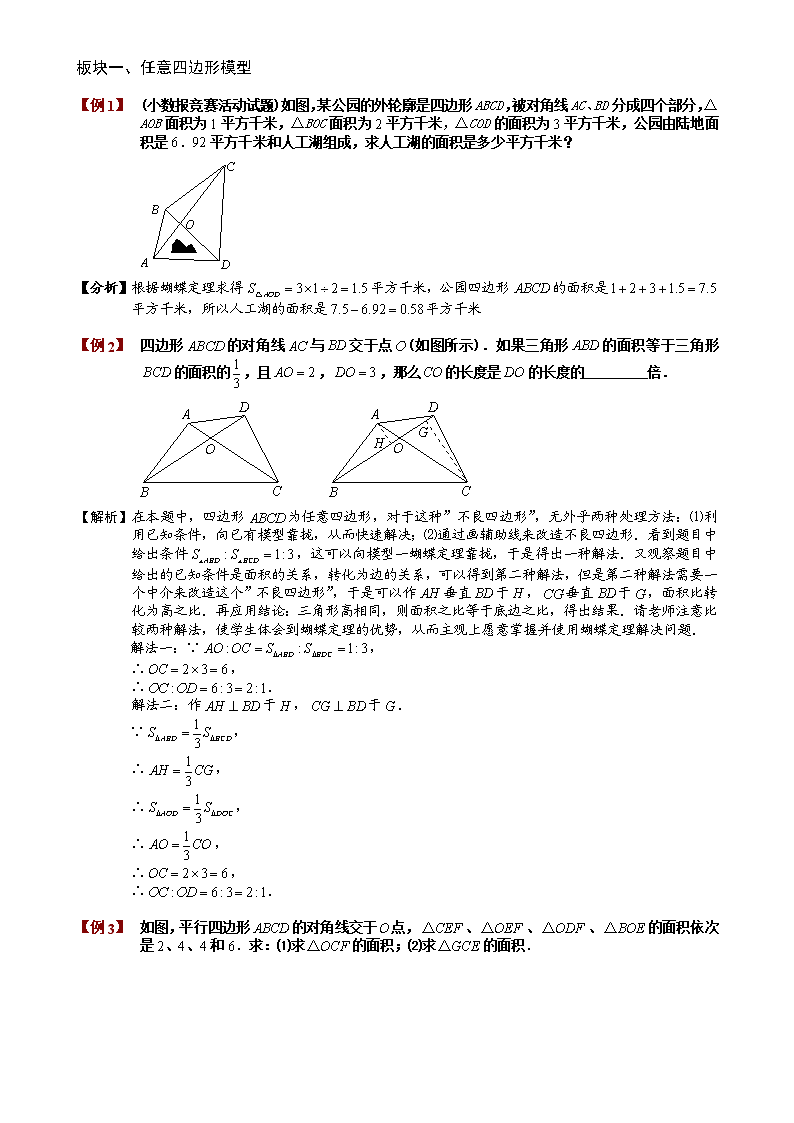
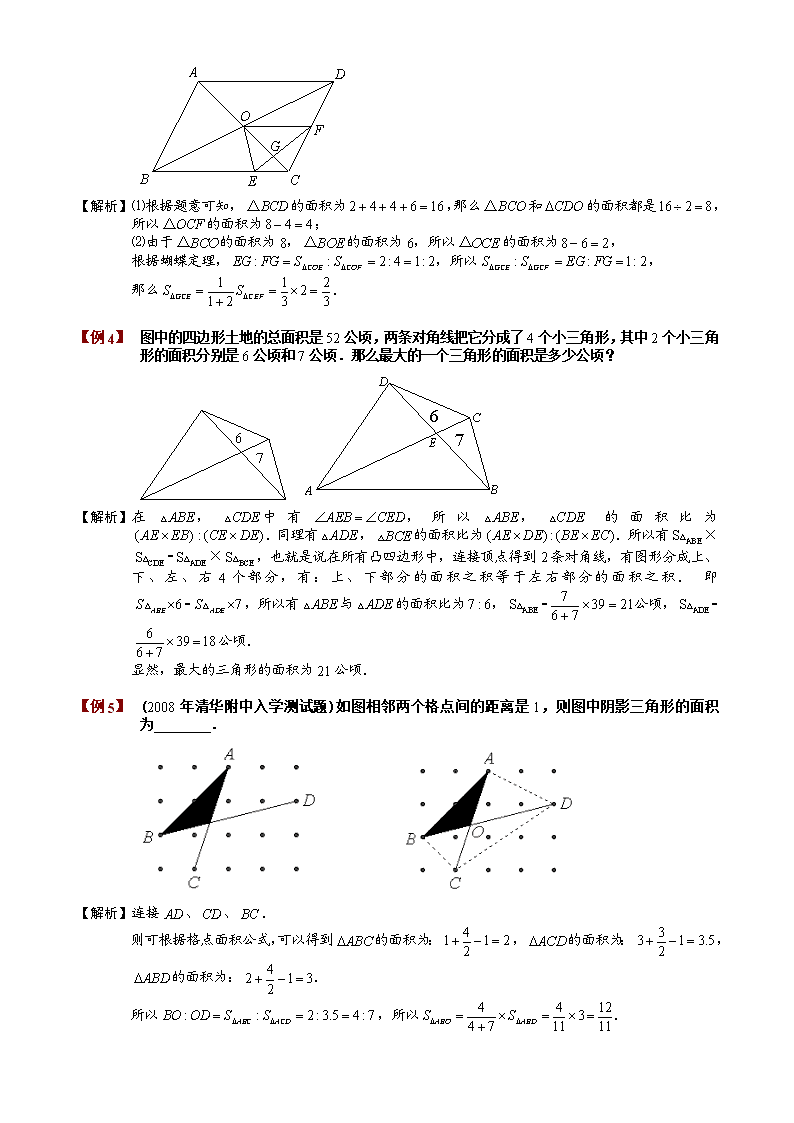
第三讲：直线型面积教学目标1、能够熟练运用任意四边型模型解题2、熟练掌握梯形模型解决特殊的四边型知识点拨一、任意四边形模型任意四边形中的比例关系(“蝴蝶定理”)：①或者②蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系．二、梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”)：①②；③的对应份数为．梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道，通过构造模型，直接应用结论，往往在题目中有事半功倍的效果．(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)例题精讲\n板块一、任意四边形模型【例1】(小数报竞赛活动试题)如图，某公园的外轮廓是四边形ABCD，被对角线AC、BD分成四个部分，△AOB面积为1平方千米，△BOC面积为2平方千米，△COD的面积为3平方千米，公园由陆地面积是6．92平方千米和人工湖组成，求人工湖的面积是多少平方千米？【分析】根据蝴蝶定理求得平方千米，公园四边形的面积是平方千米，所以人工湖的面积是平方千米【例2】四边形的对角线与交于点(如图所示)．如果三角形的面积等于三角形的面积的，且，，那么的长度是的长度的_________倍．【解析】在本题中，四边形为任意四边形，对于这种”不良四边形”，无外乎两种处理方法：⑴利用已知条件，向已有模型靠拢，从而快速解决；⑵通过画辅助线来改造不良四边形．看到题目中给出条件，这可以向模型一蝴蝶定理靠拢，于是得出一种解法．又观察题目中给出的已知条件是面积的关系，转化为边的关系，可以得到第二种解法，但是第二种解法需要一个中介来改造这个”不良四边形”，于是可以作垂直于，垂直于，面积比转化为高之比．再应用结论：三角形高相同，则面积之比等于底边之比，得出结果．请老师注意比较两种解法，使学生体会到蝴蝶定理的优势，从而主观上愿意掌握并使用蝴蝶定理解决问题．解法一：∵，∴，∴．解法二：作于，于．∵，∴，∴，∴，∴，∴．【例3】如图，平行四边形的对角线交于点，、、、的面积依次是2、4、4和6．求：⑴求的面积；⑵求的面积．\n【解析】⑴根据题意可知，的面积为，那么和的面积都是，所以的面积为；⑵由于的面积为8，的面积为6，所以的面积为，根据蝴蝶定理，，所以，那么．【例1】图中的四边形土地的总面积是52公顷，两条对角线把它分成了4个小三角形，其中2个小三角形的面积分别是6公顷和7公顷．那么最大的一个三角形的面积是多少公顷？【解析】在，中有，所以，的面积比为．同理有，的面积比为．所以有×=×，也就是说在所有凸四边形中，连接顶点得到2条对角线，有图形分成上、下、左、右4个部分，有：上、下部分的面积之积等于左右部分的面积之积．即=，所以有与的面积比为，=公顷，=公顷．显然，最大的三角形的面积为21公顷．【例2】(2008年清华附中入学测试题)如图相邻两个格点间的距离是1，则图中阴影三角形的面积为．【解析】连接、、．则可根据格点面积公式，可以得到的面积为：，的面积为：，的面积为：．所以，所以．\n【例1】(2007年人大附中考题)如图，边长为1的正方形中，，，求三角形的面积．【解析】连接．因为，，所以．因为，根据蝴蝶定理，，所以．所以，即三角形的面积是．【例2】如图，已知正方形的边长为10厘米，为中点，为中点，为中点，求三角形的面积．【解析】设与的交点为，连接、．由蝴蝶定理可知，而，，所以，故．由于为中点，所以，故，．由蝴蝶定理可知，所以，那么（平方厘米）．【例3】如图，在中，已知、分别在边、上，与相交于,若、和的面积分别是3、2、1，则的面积是．【解析】这道题给出的条件较少，需要运用共边定理和蝴蝶定理来求解．\n根据蝴蝶定理得设，根据共边定理我们可以得，，解得．【例1】(2009年迎春杯初赛六年级)正六边形的面积是2009平方厘米，分别是正六边形各边的中点；那么图中阴影六边形的面积是平方厘米．【解析】如图，设与的交点为，则图中空白部分由个与一样大小的三角形组成，只要求出了的面积，就可以求出空白部分面积，进而求出阴影部分面积．连接、、．设的面积为”“，则面积为”“，面积为”“，那么面积为的倍，为”“，梯形的面积为，的面积为”“，的面积为．根据蝴蝶定理，，故，，所以，即的面积为梯形面积的，故为六边形面积的，那么空白部分的面积为正六边形面积的，所以阴影部分面积为(平方厘米)．板块二梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”)：①②；\n③的对应份数为．梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道，通过构造模型，直接应用结论，往往在题目中有事半功倍的效果．(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)【例1】如图，，，求梯形的面积．【解析】设为份，为份，根据梯形蝴蝶定理，，所以；又因为，所以；那么，，所以梯形面积，或者根据梯形蝴蝶定理，．【例2】梯形的对角线与交于点，已知梯形上底为2，且三角形的面积等于三角形面积的，求三角形与三角形的面积之比．【解析】根据梯形蝴蝶定理，，可以求出，再根据梯形蝴蝶定理，．通过利用已有几何模型，我们轻松解决了这个问题，而没有像以前一样，为了某个条件的缺乏而千辛万苦进行构造假设，所以，请同学们一定要牢记几何模型的结论．【例3】(第十届华杯赛)如下图，四边形中，对角线和交于点，已知，并且，那么的长是多少？【解析】根据蝴蝶定理，，所以，又，所以．【例4】梯形的下底是上底的倍，三角形的面积是，问三角形的面积是多少？【解析】根据梯形蝴蝶定理，，，\n所以．【例1】如下图，一个长方形被一些直线分成了若干个小块，已知三角形的面积是，三角形的面积是，求四边形的面积．【解析】如图，连结EF，显然四边形ADEF和四边形BCEF都是梯形，于是我们可以得到三角形EFG的面积等于三角形ADG的面积；三角形BCH的面积等于三角形EFH的面积，所以四边形EGFH的面积是．【例2】如图面积为平方厘米的正方形中，是边上的三等分点，求阴影部分的面积．【解析】因为是边上的三等分点，所以，设份，根据梯形蝴蝶定理可以知道份，份，份，因此正方形的面积为份，，所以，所以平方厘米．【例3】如图，在长方形中，厘米，厘米，，求阴影部分的面积．【解析】方法一：如图，连接，将阴影部分的面积分为两个部分，其中三角形的面积为平方厘米．由于，根据梯形蝴蝶定理，，所以，而平方厘米，所以平方厘米，阴影部分的面积为平方厘米．方法二：如图，连接，，由于，设份，根据梯形蝴蝶定理，份，份，份，因此份，份，而平方厘米，所以平方厘米【例4】(2008年”奥数网杯”六年级试题)已知是平行四边形，，三角形的面积为6平方厘米．则阴影部分的面积是平方厘米．\n【解析】连接．由于是平行四边形，，所以，根据梯形蝴蝶定理，，所以(平方厘米)，(平方厘米)，又(平方厘米)，阴影部分面积为(平方厘米)．【巩固】右图中是梯形，是平行四边形，已知三角形面积如图所示(单位：平方厘米)，阴影部分的面积是平方厘米．【分析】连接．由于与是平行的，所以也是梯形，那么．根据蝴蝶定理，，故，所以(平方厘米)．【巩固】(2008年三帆中学考题)右图中是梯形，是平行四边形，已知三角形面积如图所示(单位：平方厘米)，阴影部分的面积是平方厘米．【解析】连接．由于与是平行的，所以也是梯形，那么．根据蝴蝶定理，，故，所以(平方厘米)．另解：在平行四边形中，(平方厘米)，所以(平方厘米)，根据蝴蝶定理，阴影部分的面积为(平方厘米)．【巩固】(98迎春杯初赛)如图，长方形中，阴影部分是直角三角形且面积为，的长是，的长是.那么四边形的面积是多少？【解析】因为连接知道和的面积相等即为，又因为,所以\n的面积为，根据四边形的对角线性质知道：的面积为：，所以四边形的面积为：(平方厘米).【例1】(2007年”迎春杯”高年级初赛)如图，长方形被、分成四块，已知其中3块的面积分别为2、5、8平方厘米，那么余下的四边形的面积为___________平方厘米．【解析】连接、．四边形为梯形，所以，又根据蝴蝶定理，，所以，所以(平方厘米)，(平方厘米)．那么长方形的面积为平方厘米，四边形的面积为(平方厘米)．【巩固】(98迎春杯初赛)如图，长方形中，是直角三角形且面积为54，的长是16，的长是9．那么四边形的面积是．【解析】解法一：连接，依题意，所以，则．又因为，所以，得，所以．解法二：由于，所以，而，根据蝴蝶定理，，所以，所以．【例2】如图，是等腰直角三角形，是正方形，线段与相交于点．已知正方形的面积48，，则的面积是多少？【解析】由于是正方形，所以与平行，那么四边形是梯形．在梯形中，\n和的面积是相等的．而，所以的面积是面积的，那么的面积也是面积的．由于是等腰直角三角形，如果过作的垂线，为垂足，那么是的中点，而且，可见和的面积都等于正方形面积的一半，所以的面积与正方形的面积相等，为48．那么的面积为．【例1】如图所示，是梯形，面积是，的面积是9，的面积是27．那么阴影面积是多少？【解析】根据梯形蝴蝶定理，可以得到，而(等积变换)，所以可得，并且，而，所以阴影的面积是：．课后练习练习1.(2006年南京智力数学冬令营)如下图，梯形的平行于，对角线，交于，已知与的面积分别为平方厘米与平方厘米，那么梯形的面积是________平方厘米．【解析】根据梯形蝴蝶定理，，可得，再根据梯形蝴蝶定理，，所以(平方厘米)．那么梯形的面积为(平方厘米)．练习2.如图，四边形被两条对角线分成4个三角形，其中三个三角形的面积已知，求：⑴三角形的面积；⑵？【解析】⑴根据蝴蝶定理，，那么；（2）据蝴蝶定理，．\n练习1.在下图的正方形中，是边的中点，与相交于点，三角形的面积为1平方厘米，那么正方形面积是平方厘米．【解析】连接，根据题意可知，根据蝴蝶定理得(平方厘米)，(平方厘米)，那么(平方厘米)．练习2.如图，长方形中，，，三角形的面积为平方厘米，求长方形的面积．【解析】连接，．因为，，所以．因为，，所以平方厘米，所以平方厘米．因为，所以长方形的面积是平方厘米．练习3.如图所示，、将长方形分成4块，的面积是4平方厘米，的面积是6平方厘米．问：四边形的面积是多少平方厘米？【解析】(法1)连接，根据面积比例模型或梯形蝴蝶定理，可知三角形的面积和三角形的面积相等，即其面积也是6平方厘米，再根据蝴蝶定理，三角形的面积为(平方厘米)，所以长方形的面积为(平方厘米)．四边形的面积为(平方厘米)．(法2)由题意可知，，根据相似三角形性质，，所以三角形的面积为：(平方厘米)．则三角形面积为15平方厘米，长方形面积为(平方厘米)．四边形的面积为(平方厘米)．月测备选测试1、如图，梯形中，、的面积分别为和，求梯形的面积．\n【解析】根据梯形蝴蝶定理，，所以，，，．测试2、如图，正方形面积为平方厘米，是边上的中点．求图中阴影部分的面积．【解析】因为是边上的中点，所以，根据梯形蝴蝶定理可以知道，设份，则份，所以正方形的面积为份，份，所以，所以平方厘米．测试3、(人大附中入学测试题)如图，长方形中，若三角形1的面积与三角形3的面积比为4比5，四边形2的面积为36，则三角形1的面积为________．【解析】做辅助线如下：利用梯形模型，这样发现四边形2分成左右两边，其面积正好等于三角形1和三角形3，所以1的面积就是，3的面积就是．测试4、如图，每个小方格的边长都是1，求三角形的面积．【解析】因为，且∥，所以，，．测试5、如图所示，、将长方形分成4块，的面积是5平方厘米，的面积是\n10平方厘米．问：四边形的面积是多少平方厘米？【分析】连接，根据梯形模型，可知三角形的面积和三角形的面积相等，即其面积也是10平方厘米，再根据蝴蝶定理，三角形的面积为(平方厘米)，所以长方形的面积为(平方厘米)．四边形的面积为(平方厘米)．