初中数学《全等与旋转》讲义及练习 18页

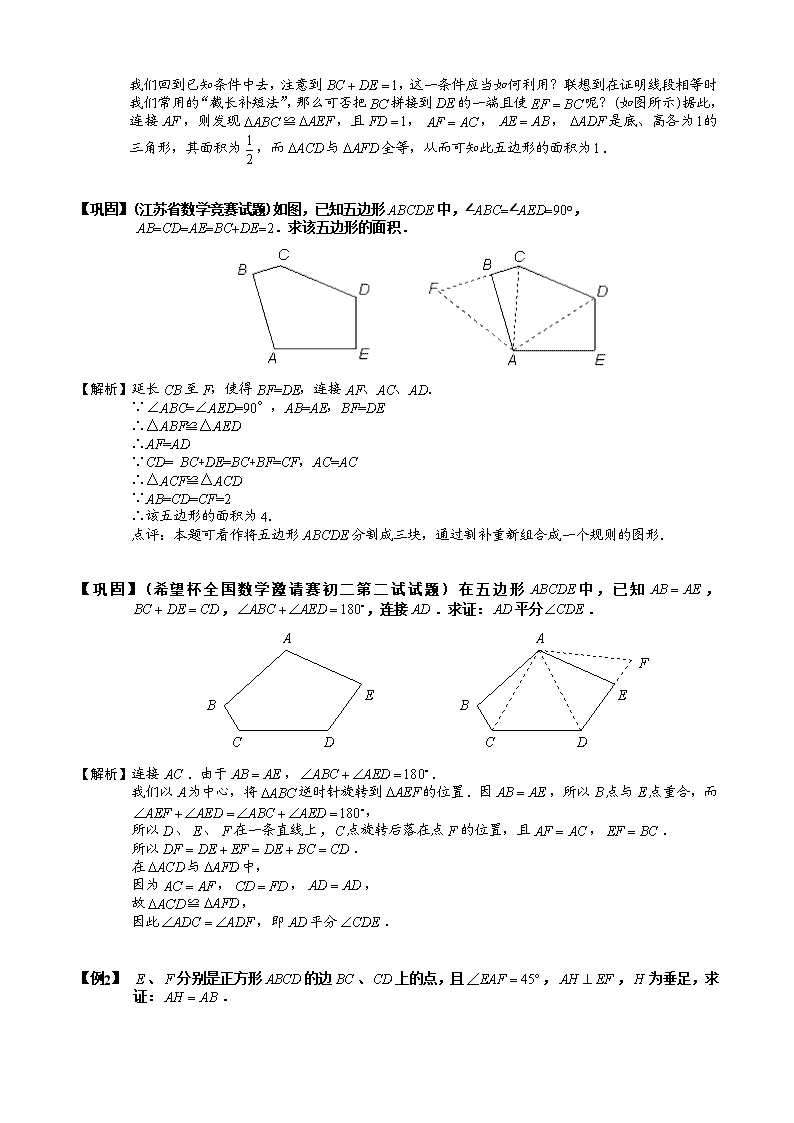
第八讲全等与旋转中考要求利用旋转的思想添加辅助线是中考常考内容，也是中考的难点。知识点睛把图形绕平面上的一个定点旋转一个角度，得到图形，这样由图形到的变换叫做旋转变换，点叫做旋转中心，叫做旋转角，叫做的象；叫做的原象，无论是什么图形，在旋转变换下，象与原象是全等形．很明显，旋转变换具有以下基本性质：①旋转变换的对应点到旋转中心的距离相等；②对应直线的交角等于旋转角．旋转变换多用在等腰三角形、正三角形、正方形等较规则的图形上，其功能还是把分散的条件集中，以便于诸条件的综合与推演．重、难点根据题目的已知条件特征，快速、正确的添加辅助线是重点和难点。例题精讲【例1】(北京市初二数学竞赛试题)如图所示，在五边形中，，，求此五边形的面积．【解析】我们马上就会想到连接、，因为其中有两个直角三角形，但又发现直接求各三角形的面积并不容易，至此思路中断．\n我们回到已知条件中去，注意到，这一条件应当如何利用？联想到在证明线段相等时我们常用的“截长补短法”，那么可否把拼接到的一端且使呢？(如图所示)据此，连接，则发现≌，且，，，是底、高各为的三角形，其面积为，而与全等，从而可知此五边形的面积为．【巩固】(江苏省数学竞赛试题)如图，已知五边形ABCDE中，∠ABC=∠AED=90°，AB=CD=AE=BC+DE=2．求该五边形的面积．【解析】延长CB至F，使得BF=DE，连接AF、AC、AD．∵∠ABC=∠AED=90°，AB=AE，BF=DE∴△ABF≌△AED∴AF=AD∵CD=BC+DE=BC+BF=CF，AC=AC∴△ACF≌△ACD∵AB=CD=CF=2∴该五边形的面积为4．点评：本题可看作将五边形ABCDE分割成三块，通过割补重新组合成一个规则的图形．【巩固】(希望杯全国数学邀请赛初二第二试试题)在五边形中，已知，，，连接．求证：平分．【解析】连接．由于，．我们以为中心，将逆时针旋转到的位置．因，所以点与点重合，而，所以、、在一条直线上，点旋转后落在点的位置，且，．所以．在与中，因为，，，故≌，因此，即平分．【例1】、分别是正方形的边、上的点，且，，为垂足，求证：．\n【解析】延长至，使，连结，易证，，．再证，全等三角形的对应高相等(利用三角形全等可证得)，则有．【巩固】如图，正方形的边长为，点在线段上运动，平分交边于点．⑴求证：．⑵设()，与的面积和是否存在最大值？若存在，求出此时的值及．若不存在，请说明理由．　　　　【解析】⑴证明：如图，延长至点，使得，连结．因为是正方形，所以在和中，，，．∴，∴，．又∵是的平分线．∴，∴．即．∵，∴，∴，∴．即．∴，得证．⑵．∵，∴由⑴知，，所以．在中，，，∴，∴．由上式可知，当达到最大值时，最大．而，所以，当时，最大值为．\n【例1】（2009平谷一模改编）如图，在直角梯形中，，，，是上一点，且，，求的长．【解析】延长到，使，连接，容易得到四边形是正方形．再延长到，使，连接，易证，∴∵，∴，∴，∴，∴．设，则．在中，，，解得，∴的长为4或6．【点评】此题直接让学生做会有较大难度，老师在讲此题之前可以先给一些提示，大概点一下思路，如果学生仍没有明确的思路，再将原型呈现给学生。此题是一道非常隐蔽的利用旋转解题的经典题目，老师可以根据此题再次跟学生强调旋转的重要性．此题原型：正方形中，分别在上，，求证：．要证此题非常简单，这是基本的旋转模型，已经在讲义中出现过很多次，老师只要把此图点出来，学生应该就明白此题的做法．【补充】如图，正方形被两条与边平行的线段分割成个小矩形，是与的交点，若矩形的面积恰是矩形面积的倍，试确定的大小，并证明你的结论．【解析】设，连接，由四边形都是矩形，可知，，，，则由是正方形，可知由①得，平方得，将②代入得，∴，得．∵，∴，即．延长到，使得，连接，\n则，那么，，∴，∵，∴，∴，即．【例1】(1997年安徽省初中数学竞赛题)在等腰的斜边上取两点、，使，记，，，则以、、为边长的三角形的形状是()．A．锐角三角形B．直角三角形C．钝角三角形D．随、、的变化而变化【解析】如图，将绕点顺时针旋转，得，连结，则，，，∴．∴，∴又易得，∴在中，有，故应选(B)【例2】(通州区2009一模第25题)请阅读下列材料：已知：如图1在中，，，点、分别为线段上两动点，若．探究线段、、三条线段之间的数量关系．小明的思路是：把绕点顺时针旋转，得到，连结，使问题得到解决．请你参考小明的思路探究并解决下列问题：⑴猜想、、三条线段之间存在的数量关系式，并对你的猜想给予证明；⑵当动点在线段上，动点运动在线段延长线上时，如图2，其它条件不变，⑴中探究的结论是否发生改变？请说明你的猜想并给予证明．【解析】⑴证明：根据绕点顺时针旋转得到∴∴，，，在中∵∴∴即∴又∵∴\n∴即∴∴∴⑵关系式仍然成立证明：将沿直线对折，得，连∴∴，，又∵，∴∵∴又∵∴∴，∴∴在中即【巩固】如图所示，在四边形ABCD中，AB=BC，∠A=∠C=90°，∠B=135°，K、N分别是AB、BC上的点，若△BKN的周长为AB的2倍，求∠KDN的度数．【解析】延长BC至F，使得CF=AB，在CF上取点E，使得CE=AK，连接BD、DE、DF．∵AB⊥AD，BC⊥CD，AB=BC∴Rt△ADB≌Rt△CDB∴AD=CD∵AD=CD，AK=CE，AB⊥AD，BC⊥CD∴△ADK≌△CDE∴DK=DE∵BK+BN+KN=2AB，BF=BN+EF+EN=2AB，EF=CF-CE=AB-AK=BK∴KN=EN∴△NDK≌△NDE∴∠KDN=∠EDN=∠CDE+∠NDC=∠CDE+∠ADK\n∵∠ABC=135°∴∠KDN=(180°-135°)=22．5°点评：本题的辅助线可以看作是将△ADB割下来，放到△CDF处，从而将不规则的图形转化为规则的图形，进而利用线段之间的等量关系求解．【例1】在等边的两边AB，AC所在直线上分别有两点M，N，D为外一点，且，，，探究：当点M，N分别在直线AB，AC上移动时，BM，NC，MN之间的数量关系及的周长与等边的周长L的关系．⑴如图①，当点M，N在边AB，AC上，且DM=DN时，BM，NC，MN之间的数量关系式__________；此时=__________⑵如图②，当点M，N在边AB，AC上，且时，猜想(1)问的两个结论还成立吗？写出你的猜想并加以证明；⑶如图③，当点M，N分别在边AB，CA的延长线上时，若AN=x，则Q=_________(用x，L表示)【解析】BM+NC=MN；(2)猜想：仍然成立证明：如图，延长AC至E，使CE=BM，连接DE由是等边三角形，，，在与中\n的周长==而等边的周长(3)【巩固】（2009房山二模）⑴如图1，在四边形中，，，分别是边上的点，且．求证：；⑵如图2，在四边形中，，，分别是边上的点，且，⑴中的结论是否仍然成立？不用证明．⑶如图3，在四边形中，，，分别是边延长线上的点，且，⑴中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．【解析】⑴延长到，使，连接．∵，，∴，∴，，∴，∴，∴，∴．∵，∴．⑵⑴中的结论仍然成立．⑶结论不成立，应该是．在上截取，使，连接．∵，，∴．∵，∴，∴．∴，∴，∴．∵，∴．\n【例1】如图，正方形内有一点，，，.（1）求的长；（2）求的大小；（3）求正方形的边长.【解析】（1）由例5可知，又，，，故（2）将绕点顺时针旋转，使于重合.设此时点位于点处，则有≌∴，，∵∴∵∴∴（此时有、、共线）（3）过点作，垂足为.∵，，∴∴【变式1】变式1中其他条件不变，，，，求的大小和正方形的面积.【解析】辅助线与解题过程与变式1类似，不再给出！，面积为.【变式2】是边长为1的正方形内一点，若，，求的大小.【解析】运用例题5的结论即可，，过程不再给出.【变式3】（西城外国语学校2007年期中试题）如图，为正三角形内一点，、、满足关系式，且，设，满足，求的值.【解析】将绕点旋转，使、重合，此时点位于点处.\n则有≌，故，.∵，∴∵，∴∵∴∴∴过点作，垂足为，则，故“希望杯”中也多次出现过这个题及其变种，应该引起重视！【变式4】（北京市数学竞赛题）如图，是边长为1的等边内任意一点，求证：.【解析】作点关于的对称点，将绕点旋转，使、重合，此时位于点处.由例6可知，∵∴∵∴≌∴由两点之间线段最短可知，，即易证，故原式得证！【例1】（2008湖北罗田改编）在中，，，以斜边为一边作正方形，正方形的中心为，求的长．【解析】在作正方形的过程中，并没有说明是向哪个方向作，所以此题需分类讨论．⑴以为边向外作正方形，如图延长到，使，连结可证\n则，是等腰直角三角形所以．⑵以为边向内作正方形，如图在上截取，连结可证则，，所以．【补充】已知正方形，在边上取一点，作交的外角平分线于，求证：．【解析】解法一：如图，连接，过作，交于．∵，，∴．又∵为等腰直角三角形，∴．又，，∴，∴，故．解法二：如图，过作，交的延长线于，连接，则，∴，∴．而，∴．又，，∴，有，∴．【例1】（2009年西城一模）已知：，以为一边作正方形，使两点落在直线AB的两侧.⑴如图，当时，求及的长；⑵当变化，且其它条件不变时，求的最大值，及相应的大小.【解析】⑴①如图1，作于点．\n∵中，，，∴，．∵，∴．在中，，∴．②解法一：如图，因为四边形为正方形，可将绕点顺时针旋转得到，可得，．∴=90°，=45°，=90°．∴．∴．解法二：如图3，过点作的平行线，与的延长线交于，的延长线交于．在中，，，，．在中，，，．在中，．⑵如图4所示，将绕点顺时针旋转得到，则的最大值即为的最大值．（见图5）∵中，，，，且两点落在直线的两侧，∴当三点共线时，取得最大值．此时，即的最大值为，此时．【补充】已知正方形和等腰，，，按图甲放置，使点在上，取的中点，连接．⑴探索的数量关系和位置关系，并说明理由；⑵将图甲中绕点顺时针旋转得图乙，连接，取的中点，问⑴中的结论是否成立？并说明理由；⑶将图甲中绕点转动任意角度（旋转角在到之间）得图丙，连接，取的中点，问⑴中的结论是否成立，请说明理由．【解析】⑴且．利用直角三角形斜边中线等于斜边一半可很容易证明．\n⑵仍然成立．延长交于点．先证明是等腰直角三角形，进而可得结论．⑶仍然成立．证法一：如图丙，延长到，使，连结可证明．∴，，又，∴．∴，∴，∴．∴．在中，是中点，∴．证法二：如图，以为边向下作正方形，延长到使．容易得到：，因此只要证明即可．由辅助线易得是等腰直角三角形，，接下来可先证明，然后再证明即可．或先证明，再证明也可．此证法将要证线段通过中位线都扩大了两倍，然后再通过全等证明线段相等，观察图形其本质也是利用旋转在构造全等三角形．证法三：如图，分别取中点为，连结．观察后很容易发现：只要证明，问题马上就可以解决．而且不难发现证明全等的条件也是够的：，且，∴，∴，同时也很容易证明．此证法利用了中位线和直角三角形斜边中线的性质构造线段相等，【例1】如图所示，在每一条边上分别向形外作正方形，正方形和正方形.连接、、，是的中线.求证：.\n【解析】解法１：可知，如果能够证明的中位线等于，问题就解决了，于是取、的中点、，连接.找与全等三角形，可知该三角形必有一边与相等，于是取的中点，连接.由于，，故与互补，又，故与互补，从而可知.又，，，故，从而≌，则，即．解法2：“解法1”中，与直接全等的三角形没有，下面构造与直接全等的辅助线．延长至点，使得，连接，并取其中点，连接.由、可知.易证≌(相当于绕点顺时针旋转)，从而(全等三角形对应边上的中线相等，这是全等三角形的一条性质)，取、的中点、，连接、，同样有，．【补充】两张大小适当的正方形纸片，如图所示重叠放在一起，重叠部分是一个凸八边形．对角线，分这个八边形为四个小的凸四边形．请你证明且．【解析】延长，相交于点，延长，相交于点，延长相交与点，延长相交于点．则四边形、都是平行四边形，易知,作于；作于；在Rt与中，,,所以RTRt，因此，作于；作于；\n同理可证RtRt,从而，易证(SAS)所以．再由RtRt，推得,又所以，即．家庭作业【习题1】（2009甘肃定西）如图，四边形中，，，于点，且四边形的面积为，则____________．【解析】【习题2】如图，已知和都是等边三角形，、、在一条直线上，试说明与相等的理由．【解析】∵，，∴∴又∵∴【习题3】（2007年北京市中考第21题第(2)问）在平面直角坐标系中，为正方形，点的坐标为（1，1），将一个最短边长大于的直角三角形纸片的直角顶点放在对角线上，若三角形纸片的直角顶点不与点、重合，且两条直角边与正方形相邻两边相交，当这个三角形纸片与正方形重叠部分的面积是正方形面积的一半时，试确定三角形纸片直角顶点的坐标.\n【解析】直角顶点的坐标为或，此时的图形如右图.【习题1】如图，点为线段上一点，、是等边三角形，是中点，是中点，求证：是等边三角形．【解析】∵，∴，又∵、分别是、的中点，∴，∴，∴∴是等边三角形月测备选【备选1】如图，正方形ABCD的边长为1，AB、AD上各存一点P、Q，若△APQ的周长为2，求∠PCQ的度数．【解析】把△CDQ绕点C旋转90°到△CBF的位置，CQ=CF．∵AQ+AP+QP=2，又AQ+QD+AP+PB=2，∴QD+BP=QP．又DQ=BF，∴PQ=PF．∴．∴．又∵∠QCF=90°，∴∠PCQ=45°．【备选2】已知：如图，点为线段上一点，、是等边三角形．求证：平分\n．【解析】过点作于，于，由，利用进而再证，可得到，故平分．【备选1】(湖北省黄冈市2008年初中毕业生升学考试)已知：如图，点是正方形的边上任意一点，过点作交的延长线于点．求证：．【解析】∵∴在和中∴∴【备选2】(北京市数学竞赛试题，天津市数学竞赛试题)如图所示，是边长为的正三角形，是顶角为的等腰三角形，以为顶点作一个的，点、分别在、上，求的周长．【解析】如图所示，延长到使．在与中，因为，，，所以，故．因为，，所以．又因为，所以．在与中，，，，\n所以，则，所以的周长为．