初中代数式练习专项 12页

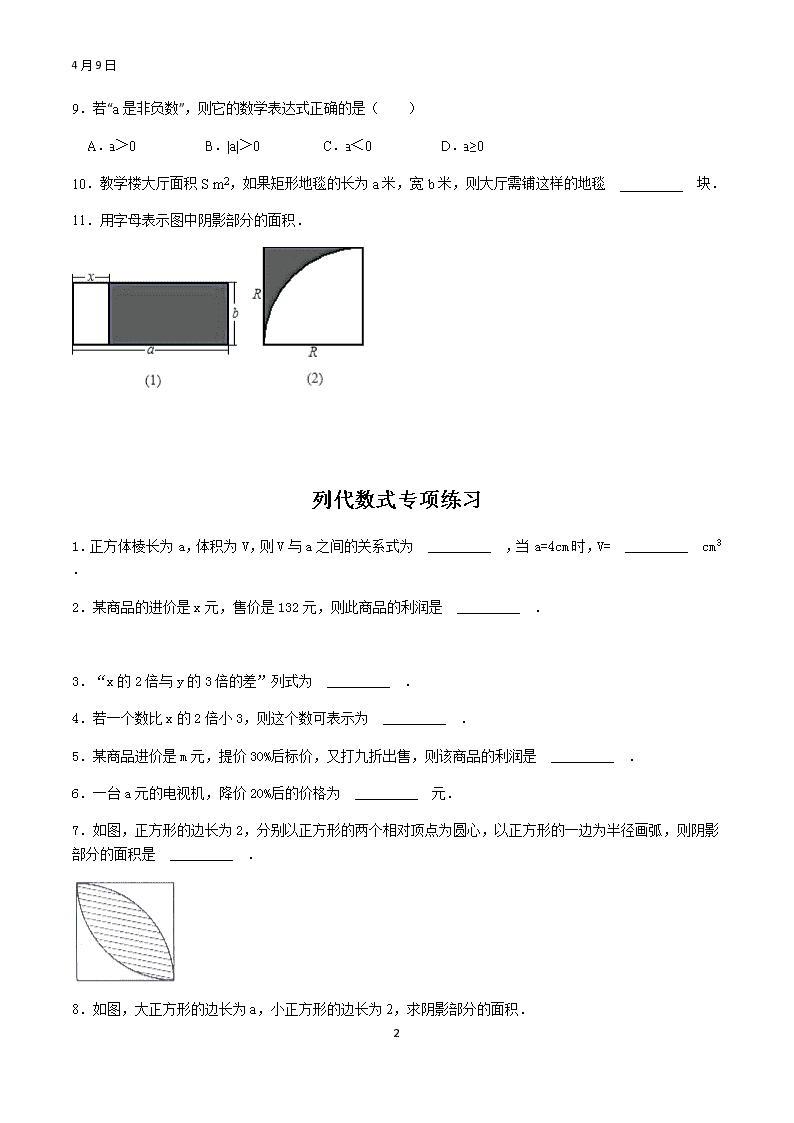
4月9日代数式的认识意义专项1．用﹣a表示的一定是（　　）　A．正数B．负数C．正数或负数D．以上都不对　2．下列代数式中符合书写要求的是（　　）　A．B．n2C．a÷bD．3．用代数式表示“x与y的2倍的和”，正确的一个是（　　）　A．2x+2yB．2x+yC．x+2yD．x2+y2　4．代数式y2﹣x用语言叙述正确的是（　　）　A．y与x的平方差B．y与x差的平方C．x的平方与y的差D．y的平方与x的差5．下列各式，代数式的个数是（　　）①x+6②a2+b=b+a2③4x+1＞7④b⑤0⑥⑦4a+3≠0⑧23﹣6⑨8m﹣2n＜0．　A．4个B．5个C．6个D．7个．6．a千克盐水中有水b千克，m千克这样的盐水中含盐（　　）　A．m千克B．m千克C．m千克D．m千克7．某商品八折出售，“八折”表示的含义是（　　）　A．比原价少80%B．是原价的80%　C．比原价少80～100元D．比原价少80%元8．水结成冰体积增大，现有体积为a的水结成冰后体积为（　　）　A．aB．aC．aD．a12\n4月9日9．若“a是非负数”，则它的数学表达式正确的是（　　）　A．a＞0B．|a|＞0C．a＜0D．a≥010．教学楼大厅面积Sm2，如果矩形地毯的长为a米，宽b米，则大厅需铺这样的地毯　_________　块．11．用字母表示图中阴影部分的面积．列代数式专项练习1．正方体棱长为a，体积为V，则V与a之间的关系式为　_________　，当a=4cm时，V=　_________　cm3．2．某商品的进价是x元，售价是132元，则此商品的利润是　_________　．　3．“x的2倍与y的3倍的差”列式为　_________　．4．若一个数比x的2倍小3，则这个数可表示为　_________　．5．某商品进价是m元，提价30%后标价，又打九折出售，则该商品的利润是　_________　．6．一台a元的电视机，降价20%后的价格为　_________　元．7．如图，正方形的边长为2，分别以正方形的两个相对顶点为圆心，以正方形的一边为半径画弧，则阴影部分的面积是　_________　．8．如图，大正方形的边长为a，小正方形的边长为2，求阴影部分的面积．12\n4月9日9．绥阳某商店的一种商品每件进价为a元，按进价提高30%标价，再按标价的8折出售，那么打折后，每件商品的售价是　_________　元．10．晓霞的爸爸开了一个超市，一天，她爸爸分别以P元进了A、B两种商品，后来A商品提价20%，B商品降价10%，这样在某一天中，A商品卖了10件，B商品卖了20件，问这一天里超市作这两种买卖是赚了还是赔了？并说明理由．11．为了节约用水，某市决定调整居民用水收费方法，规定：如果每户每月用水不超过20吨，每吨水收费3元，如果每户每月用水超过20吨，则超过部分每吨水收费3.8元；小红看到这种收费方法后，想算算她家每月的水费，但是她不清楚家里每月的用水是否超过20吨．（1）如果小红家每月用水15吨，水费是多少．如果每月用水35吨，水费是多少；（2）如果字母x表示小红家每月用水的吨数，那么小红家每月的水费该如何用x的代数式表示呢．12．某公园的成人票价是20元，儿童票价是8元，甲旅行团有x名成人和y名儿童；乙旅行团的成人数是甲旅行团的2倍，儿童人数是甲旅行团的．（1）求两个旅行团的门票总费用是多少？（2）当x=10人，y=6人时，求两个旅行团的门票总费用是多少元？　12\n4月9日13．小明想把一长是60cm，宽为40cm的长方形硬纸片做成一个无盖的长方体盒子，于是在长方形的四个角各剪去一个相同小正方形（如图）．（1）若设这些小正方形的边长为xcm，求图中阴影部分小长方形的面积．（2）当x=5时，求这个盒子的体积．14．一个三位数，个位上的数是十位上的数的平方，百位上的数比十位上的数的4倍多1．将十位上的数设为x．（1）列式表示这个三位数；（2）这个三位数是多少？15．学校组织初一年级全体同学参加植树造林劳动．全体同学分三队，第一队植树x棵，第二队植的树比第一队植树的两倍少80棵，第三队植的树比第二队植树多了10%．（1）求全体同学一共植树多少棵？（用含x的式子表示）（2）若x=100棵，求全体同学共植树多少棵？16．用代数式表示下列图形中阴影部分的面积．（1）S阴影=　_________　；（2）S阴影=　_________　．　12\n4月9日17．一本小说共m页，一位同学第一天看了全书的少6页，第二天看了剩下的多6页，第三天把剩下的全部看完，该同学第三天看了多少页？若m=900，则第三天看了多少页？求代数式的值专项练习1．若a2﹣3a=1，则代数式2a2﹣6a+5的值是　_________　．2.若a2+2a=1，则（a+1）2=　_________　．3．若a、b互为相反数，x、y互为倒数，则式子2（a+b）+5xy的值为　_________　．4．a，b互为相反数，a≠0，c、d互为倒数，则式子的值为　_________　．5．若m=n﹣5，则5m﹣5n+5等于　_________　．6．若代数式a﹣b的值是1，那么代数式2a﹣（3+2b）的值等于　_________　．7．若x2﹣2x的值是6，则﹣3x2+6x+5的值是　_________　．8．已知：a2+ab=5，b2+ab=2，则a2+2ab+b2=　_________　．9．若m2+2m﹣2=0，则2m2+4m﹣9=　_________　．10．已知多项式3x2﹣4x+6的值为9，则多项式的值为　_________　．11．若（3+a）2+|b﹣2|=0，则3a﹣2b﹣2012的值为　_________　．12．已知a2+5ab=76，3b2+2ab=51，求代数式a2+11ab+9b2的值．13．当x=7时，代数式ax3+bx﹣5的值为7；当x=﹣7时，代数式ax3+bx﹣5的值为多少？14．三个有理数a，b，c的积是负数，其和为正数，当x=++时，试求x2011﹣2010x+2009的值．15．若|x﹣4|+（2y﹣x）2=0，求代数式x2﹣2xy+y2的值．12\n4月9日　16．已知|m|=3，n2=16，且mn＜0，求2m﹣3n的值．17．已知m2﹣mn=21，mn﹣n2=﹣12．求下列代数式的值：（1）m2﹣n2（2）m2﹣2mn+n2．　18．a※b是新规定的这样一种运算法则：a※b=a2+2ab，例如3※（﹣2）=32+2×3×（﹣2）=﹣3（1）试求（﹣2）※3的值（2）若1※x=3，求x的值（3）若（﹣2）※x=﹣2+x，求x的值　19．已知，求代数式的值．合并同类项专项练习1.2.﹣0.8a2b﹣6ab﹣3.2a2b+5ab+a2b；12\n4月9日3.5（a﹣b）2﹣3（a﹣b）2﹣7（a﹣b）﹣（a﹣b）2+7（a﹣b）．4.3（a2﹣2a﹣3）﹣5（﹣5a2﹣2）5．6．5m2﹣7n﹣8mn+5n﹣9m2+8mn7.﹣5yx2+4xy2﹣2xy+6x2y+2xy+5．8.．整式的加减专项练习124月9日1、x+［x+(-2x-4y)］　 2、(a+4b)-(3a-6b)3、3x2-1-2x-5+3x-x2 4、(a+4b)-(3a-6b)5、4x+2y—5x—y　　6、—3ab+7—2a2—9ab—37、-0.8a2b-6ab-1.2a2b+5ab+a2b124月9日124月9日8、9、6x2y+2xy-3x2y2-7x-5yx-4y2x2-6x2y10、12\n4月9日11、12、13、14、15、4x2y-8xy2+7-4x2y+12xy2-416、a2-2ab+b2+2a2+2ab-b2124月9日17、先化简,再求值:,其中.18、化简:.19、其中：20、已知：A=，B=，求（3A-2B）－（2A+B）的值。12\n4月9日21、若，求3a2b－[2ab2－2（ab－1.5a2b）+ab]+3ab2的值；整式的加减化简求值专项练习1．先化简再求值：2（3a2﹣ab）﹣3（2a2﹣ab），其中a=﹣2，b=3．　2．先化简再求值：6a2b﹣（﹣3a2b+5ab2）﹣2（5a2b﹣3ab2），其中．　3．先化简，再求值：3x2y2﹣[5xy2﹣（4xy2﹣3）+2x2y2]，其中x=﹣3，y=2．　4．先化简，再求值：5ab2+3a2b﹣3（a2b﹣ab2），其中a=2，b=﹣1．　5．先化简再求值：2x2﹣y2+（2y2﹣x2）﹣3（x2+2y2），其中x=3，y=﹣2．　6．先化简，再求值：a2﹣（2a2+2ab﹣b2）+（a2﹣ab﹣b2），其中a=3，b=﹣2．　7．先化简再求值：3a2﹣（2ab+b2）+（﹣a2+ab+2b2），其中a=﹣1，b=2．　12\n4月9日8．化简求值：3a2b﹣〔2ab2﹣2（ab﹣a2b）+ab〕+3ab2，其中a=3，b=﹣．　9．已知3xa﹣2y2z3和﹣4x3yb﹣1z3是同类项，求3a2b﹣[2ab2﹣2（a2b+2ab2）]的值．　10．先化简，再求值：﹣8xy2+3xy﹣2（xy2﹣xy），其中x=，y=﹣2．代数式典型例题1．已知7xmy3和﹣是同类项，则（﹣n）m=　_________　．　2．若单项式3x4yn与﹣2x2m+3y3的和仍是单项式，则（4m﹣n）n=　_________　．　3．已知x5yn与﹣3x2m+1y3n﹣2是同类项，则m+n=　_________　．　4．已知﹣3x4+my与x4y3n是同类项，求代数式m100+（﹣3n）99﹣mn的值．　5．已知关于多项式mx2+4xy﹣x﹣2x2+2nxy﹣3y合并后不含有二次项，求nm的值．　12\n4月9日6．若关于x、y的方程6x+5y﹣2﹣3Rx﹣2Ry+4R=0合并同类项后不含y项，求R的值．　7．k为何值时，多项式x2﹣2kxy﹣3y2+6xy﹣x﹣y中，不含x，y的乘积项．　8．先去括号，后合并同类项：（1）x+[﹣x﹣2（x﹣2y）]；（2）；（3）2a﹣（5a﹣3b）+3（2a﹣b）；（4）﹣3{﹣3[﹣3（2x+x2）﹣3（x﹣x2）﹣3]}．　9．观察下列各等式，并回答问题：；；；；…（1）填空：=　_________　（n是正整数）；（2）计算：…．　12\n4月9日12