初中数学存在性问题专题强化练习 10页

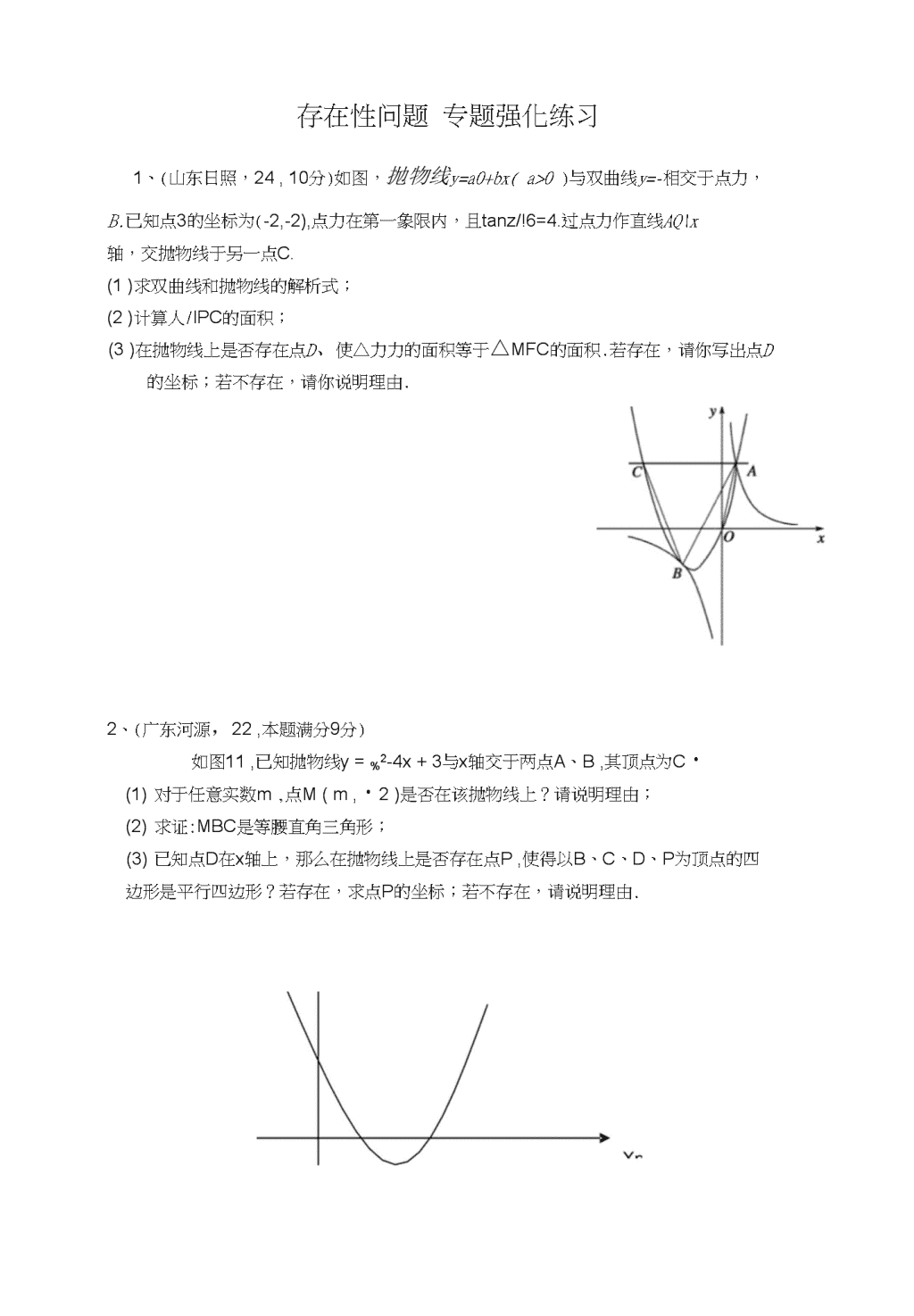
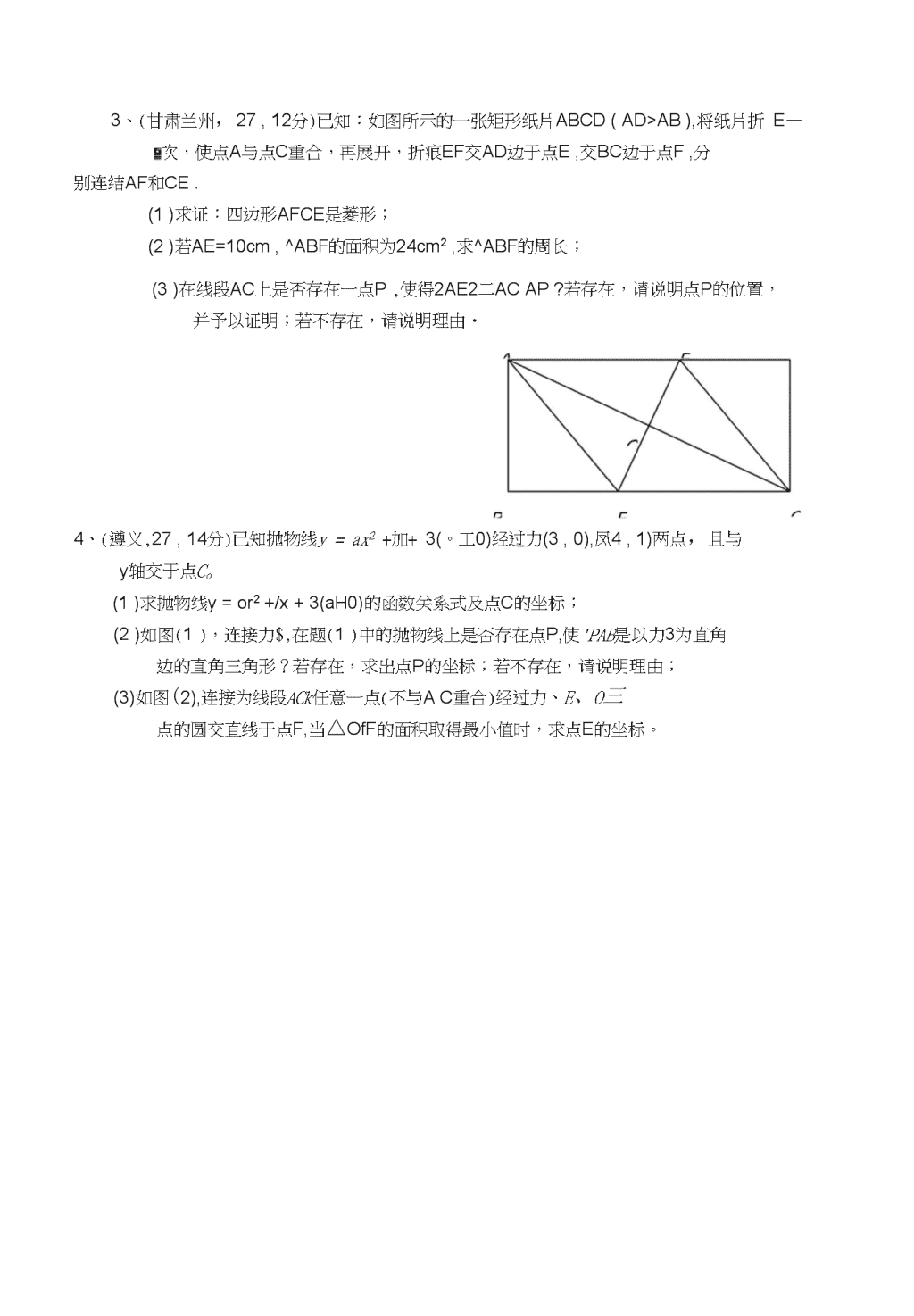
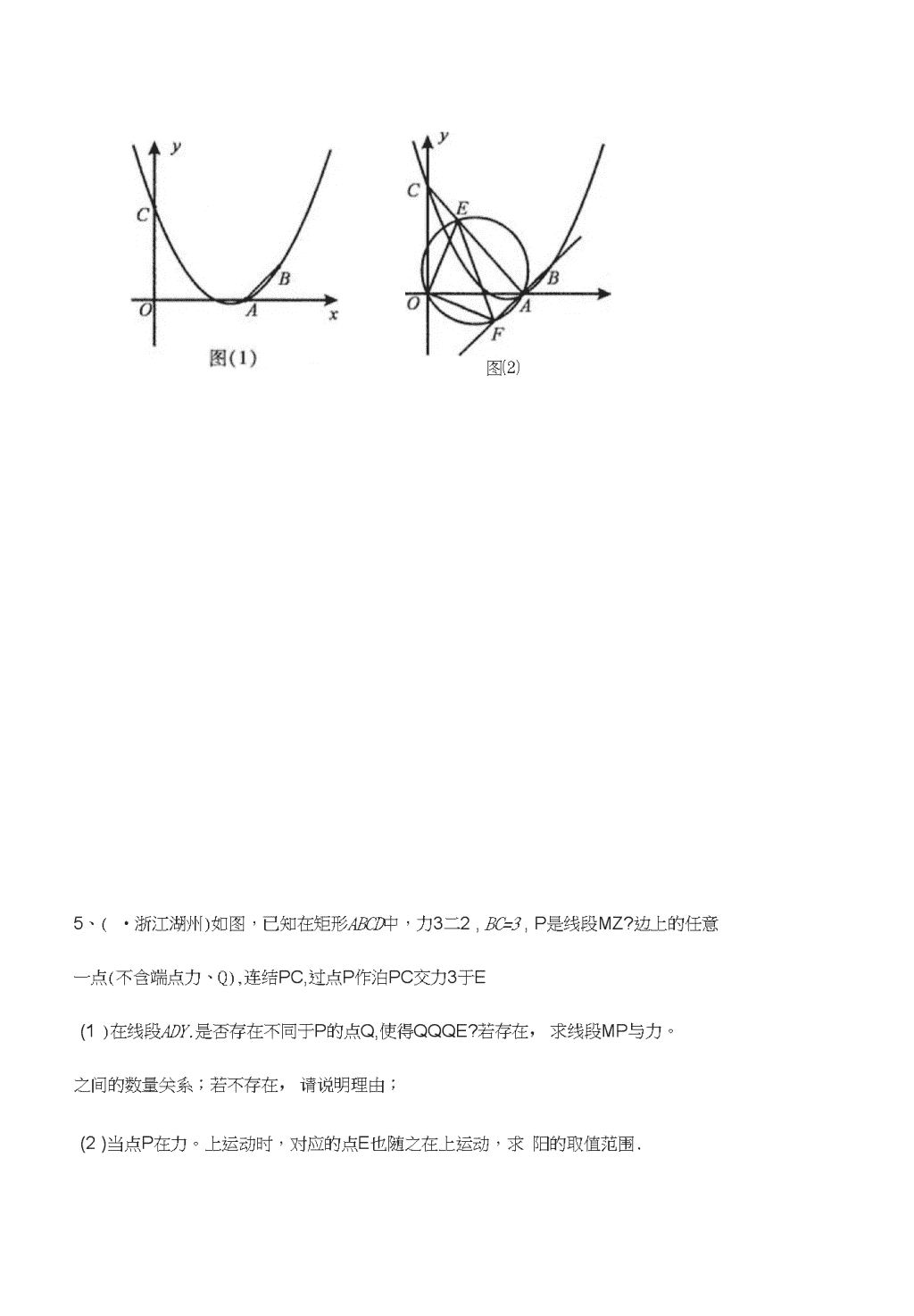
存在性问题专题强化练习1、(山东日照，24,10分)如图，抛物线y=a0+bx(a>0)与双曲线y=-相交于点力，B.已知点3的坐标为(-2,-2),点力在第一象限内，且tanz/!6=4.过点力作直线AQ\x轴，交抛物线于另一点C.(1)求双曲线和抛物线的解析式；(2)计算人/lPC的面积；(3)在抛物线上是否存在点D、使△力力的面积等于△MFC的面积.若存在，请你写岀点D的坐标；若不存在，请你说明理由.2、(广东河源，22,本题满分9分)如图11,已知抛物线y=%2-4x+3与x轴交于两点A、B,其顶点为C・(1)对于任意实数m,点M(m,・2)是否在该抛物线上？请说明理由；(2)求证:MBC是等腰直角三角形；(3)已知点D在x轴上，那么在抛物线上是否存在点P,使得以B、C、D、P为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由.\n3、(甘肃兰州，27,12分)已知：如图所示的一张矩形纸片ABCD(AD>AB),将纸片折E—次，使点A与点C重合，再展开，折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.(1)求证：四边形AFCE是菱形；(2)若AE=10cm,^ABF的面积为24cm2,求^ABF的周长；(3)在线段AC上是否存在一点P,使得2AE2二ACAP?若存在，请说明点P的位置，并予以证明；若不存在，请说明理由・4、(遵义,27,14分)已知抛物线y=ax2+加+3(。工0)经过力(3,0),凤4,1)两点，且与y轴交于点Co(1)求抛物线y=or2+/x+3(aH0)的函数关系式及点C的坐标；(2)如图(1)，连接力$,在题(1)中的抛物线上是否存在点P,使'PAB是以力3为直角边的直角三角形？若存在，求岀点P的坐标；若不存在，请说明理由；(3)如图(2),连接为线段ACk任意一点(不与AC重合)经过力、E、O三点的圆交直线于点F,当△OfF的面积取得最小值时，求点E的坐标。\n图⑵5、(•浙江湖州)如图，已知在矩形ABCD中，力3二2,BC=3,P是线段MZ?边上的任意一点(不含端点力、Q),连结PC,过点P作泊PC交力3于E(1)在线段ADY.是否存在不同于P的点Q,使得QQQE?若存在，求线段MP与力。之间的数量关系；若不存在，请说明理由；(2)当点P在力。上运动时，对应的点E也随之在上运动，求阳的取值范围.\n6、(•山东潍坊)如图，已知正方形OABC在直角坐标系xOy中，点A、C分别在x轴、y轴的正半轴上，点O在坐标原点.等腰直角三角板OEF的直角顶点O在原点，E、F分别在04、0C上，且04=4,0E=2.将三角板OEF绕0点逆时针旋转至0E、片的位置，连结CF；,AE、.(1)求证：△0A&QbOCF\・(2)若三角板OEF绕0点逆时针旋转一周，是否存在某一位置，使得OE〃CF.若存在，请求出此时E点的坐标；若不存在，请说明理由.\n7、(•湖南郴州)如图，已知正比例函数和反比例函数的图像都经过点・2,・1),且P(・1,・2)为双曲线上的一点，Q为坐标平面上一动点，Q4垂直于"轴，Q8垂直于y轴，垂足分别是力、B.(1)写出正比例函数和反比例函数的关系式；(2)当点Q在直线加上运动时,直线〃O上是否存在这样的点Q,使得'OBQ与△O4P面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由；(3)如图12,当点Q在第一象限中的双曲线上运动时，作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.\n7、(•湖南郴州)如图，已知正比例函数和反比例函数的图像都经过点・2,・1),且P(・1,・2)为双曲线上的一点，Q为坐标平面上一动点，Q4垂直于"轴，Q8垂直于y轴，垂足分别是力、B.(1)写出正比例函数和反比例函数的关系式；(2)当点Q在直线加上运动时,直线〃O上是否存在这样的点Q,使得'OBQ与△O4P面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由；(3)如图12,当点Q在第一象限中的双曲线上运动时，作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.\n8、(•黑龙江牡丹江)如图，UABCD在平面直角坐标系中，AD=6,若OA、0B的长是关于兀的一元二次方程x2-7x+12=0的两个根，且(1)求sinZABC的值.(2)若疋为兀轴上的点，且S^A0E=—，求经过D、E两点的直线的解析式，并判断3△AOE与△D40是否相似？(3)若点M在平面直角坐标系内，则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形？若存在，请直接写出F点的坐标；若不存在，请说明理由.9、(•江苏扬州)在'ABC中，zC=90°,AC=3,BC=4,CQ是斜边力3上的高,点E在斜边ABk,过点F作直线与△SBC的直角边相交于点F,设AE=x,的面积为y.(1)求线段/IQ的长；(2)若EFiAB,当点E在线段ABk移动时，①求卩与x的函数关系式(写出自变量x的取值范围)②当"取何值时，p有最大值？并求其最大值；(3)若F在直角边ACk(点F与4C两点均不重合)，点F在斜边ABk移动，试问：是否存在直线EF将'ABC的周长和面积同时平分？若存在直线EF,求出"的值；若不存\n在直线FF,请说明理由・备用图10.(•山东威海)(1)探究新知：①如图①，已知AD^BC,AD=BCy点〃，AZ是直线CZ?上任意两点.求证1ABM与'ABN的面积相等.图①圉②②如图②，已知AD\BE.AD=BE、AE^CC^EF,点〃是直线CQ上任一点，点G是直线FF上任一点.试判断△力酗与a/IBG的面积是否相等，并说明理由.(2)结论应用：如图③，抛物线y=ax2-^-bx+c的顶点为C(1,4),交x轴于点/!(3,0),交y轴于点Q.试探究在抛物线y=aF+bx+c上是否存在除点C以外的点F,使得"QE\n与的面积相等？若存在，请求岀此时点F的坐标，若不存在，请说明理由.(友情提示：解答本问题过程中，可以直接使用“探究新知”中的结论.)\n