初中数学综合测试及答案 7页

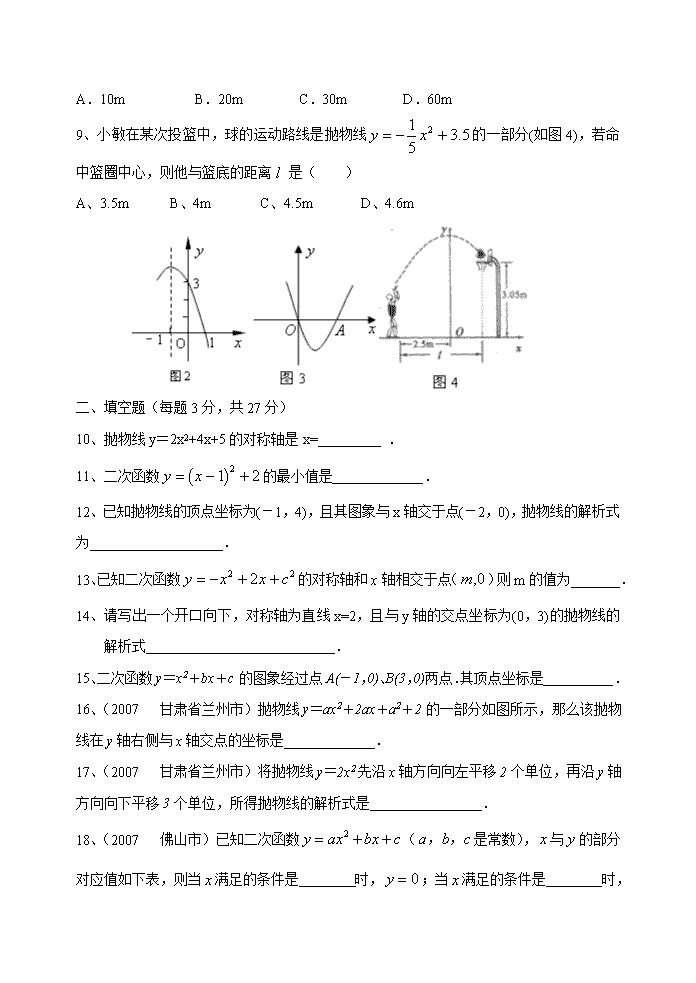
初中数学综合测试及答案一、选择题（每题4分，共36分）1、抛物线y=3(x-1)+1的顶点坐标是（）A．（1，1）B．（-1，1）C．（-1，-1）D．（1，-1）2、二次函数的图像与x轴交点的横坐标是（）A.-2和-3B.-2和3C.2和3D.2和-33、抛物线的一部分如图1所示，该抛物线在轴右侧部分与轴交点的坐标是（）A、（，0）B、（1，0）C、（2，0）D、（3，0）4、（2007长沙市）把抛物线向上平移个单位，得到的抛物线是（）CA．B．C．D．5、若抛物线与轴的交点为，则下列说法不正确的是（）A．抛物线开口向上B．抛物线的对称轴是C．当时，的最大值为D．抛物线与轴的交点为6、抛物线的部分图象如图2所示，若，则的取值范围是（）A.B.C.或D.或7、（2007常州市）若二次函数（为常数）的图象如下（图3），则的值为（）A．B．C．D．8、一个运动员打尔夫球，若球的飞行高度与水平距离之间的函数表达式为，则高尔夫球在飞行过程中的最大高度为（）\nA．10mB．20mC．30mD．60m9、小敏在某次投篮中，球的运动路线是抛物线的一部分(如图4)，若命中篮圈中心，则他与篮底的距离是（）A、3.5mB、4mC、4.5mD、4.6m二、填空题（每题3分，共27分）10、抛物线y＝2x2+4x+5的对称轴是x=_________．11、二次函数的最小值是_____________．12、已知抛物线的顶点坐标为(－1，4)，且其图象与x轴交于点(－2，0)，抛物线的解析式为___________________．13、已知二次函数的对称轴和x轴相交于点（）则m的值为_______．14、请写出一个开口向下，对称轴为直线x=2，且与y轴的交点坐标为(0，3)的抛物线的解析式．15、二次函数y＝x2＋bx＋c的图象经过点A(－1，0)、B(3，0)两点．其顶点坐标是__________．16、（2007甘肃省兰州市）抛物线y＝ax2＋2ax＋a2＋2的一部分如图所示，那么该抛物线在y轴右侧与x轴交点的坐标是_____________．17、（2007甘肃省兰州市）将抛物线y＝2x2先沿x轴方向向左平移2个单位，再沿y轴方向向下平移3个单位，所得抛物线的解析式是________________．18、（2007佛山市）已知二次函数（是常数），与的部分对应值如下表，则当满足的条件是时，；当满足的条件是时，\n．0123020图9三、解答题（共57分）19、（8分）二次函数的图象如图9所示，根据图象解答下列问题：（1）写出方程的两个根．（2）写出不等式的解集．（3）写出随的增大而减小的自变量的取值范围．（4）若方程有两个不相等的实数根，求的取值范围．20、（12分）（1）把二次函数代成的形式．（2）写出抛物线的顶点坐标和对称轴，并说明该抛物线是由哪一条形如的抛物线经过怎样的变换得到的？（3）如果抛物线中，的取值范围是，请画出图象，并试着给该抛物线编一个具有实际意义的情境（如喷水、掷物、投篮等）．21、（12分）某水果批发商销售每箱进价为40元的苹果，物价部门规定每箱售价不得高于55元，市场调查发现，若每箱以50元的价格调查，平均每天销售90箱，价格每提高1元，平均每天少销售3箱．（1）求平均每天销售量（箱）与销售价（元/箱）之间的函数关系式．（2）求该批发商平均每天的销售利润（元）与销售价（元/箱）之间的函数关系式．（3）当每箱苹果的销售价为多少元时，可以获得最大利润？最大利润是多少？\n22、（12分）如图，足球场上守门员在处开出一高球，球从离地面1米的处飞出（在轴上），运动员乙在距点6米的处发现球在自己头的正上方达到最高点，距地面约4米高，球落地后又一次弹起．据实验，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半．（1）求足球开始飞出到第一次落地时，该抛物线的表达式．（2）足球第一次落地点距守门员多少米？（取）（3）运动员乙要抢到第二个落点，他应再向前跑多少米？（取）23、（2007安徽省）（13分）按右图所示的流程，输入一个数据x，根据y与x的关系式就输出一个数据y，这样可以将一组数据变换成另一组新的数据，要使任意一组都在20～100（含20和100）之间的数据，变换成一组新数据后能满足下列两个要求：（Ⅰ）新数据都在60～100（含60和100）之间；（Ⅱ）新数据之间的大小关系与原数据之间的大小关系一致，即原数据大的对应的新数据也较大．（1）若y与x的关系是y＝x＋p(100－x)，请说明：当p＝时，这种变换满足上述两个要求；（2）若按关系式y=a(x－h)2＋k　(a>0)将数据进行变换，请写出一个满足上述要求的这种关系式．（不要求对关系式符合题意作说明，但要写出关系式得出的主要过程）\n参考答案：一、1、A2、D3、B4、C5、C6、B7、D8、A9、B二、10、－111、212、y=－4(x+1)2+413、114、y=－(x－1)2+715、(1，－4)16、(1，0)17、y＝2x2＋8x＋518、0或2；三、19、（1），（2）（3）（4）20、解：（1）．（2）由上式可知抛物线的顶点坐标为，其对称轴为直线yx310该抛物线是由抛物线向右平移1个单位，再向上平移3个单位（或向上平移3个单位，再向右平移1个单位）得到的．（3）抛物线与轴交于，与轴交于，顶点为，把这三个点用平滑的曲线连接起来就得到抛物线在的图象（如图所示）．（画出的图象没有标注以上三点的减1分）情境示例：小明在平台上，从离地面2.25米处抛出一物体，落在离平台底部水平距离为3米的地面上，物体离地面的最大高度为3米．（学生叙述的情境只要符合所画出的抛物线即可）21、（1）化简得：\n（2）（3），抛物线开口向下．当时，有最大值又，随的增大而增大当元时，的最大值为元当每箱苹果的销售价为元时，可以获得元的最大利润．22、解：（1）如图，设第一次落地时，抛物线的表达式为由已知：当时即表达式为（或）（2）（3分）令（舍去）．足球第一次落地距守门员约13米．（3）如图，第二次足球弹出后的距离为根据题意：（即相当于将抛物线向下平移了2个单位）解得\n（米）．23、（1）当P=时，y=x＋,即y=．∴y随着x的增大而增大，即P=时，满足条件（Ⅱ）又当x=20时，y==100．而原数据都在20～100之间，所以新数据都在60～100之间，即满足条件（Ⅰ），综上可知，当P=时，这种变换满足要求；（2）本题是开放性问题，答案不唯一．若所给出的关系式满足：（a）h≤20；（b）若x=20,100时，y的对应值m，n能落在60～100之间，则这样的关系式都符合要求．如取h=20,y=,∵a＞0，∴当20≤x≤100时，y随着x的增大令x=20,y=60，得k=60　①令x=100,y=100，得a×802＋k=100②由①②解得，∴．