- 1.84 MB
- 2022-09-01 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
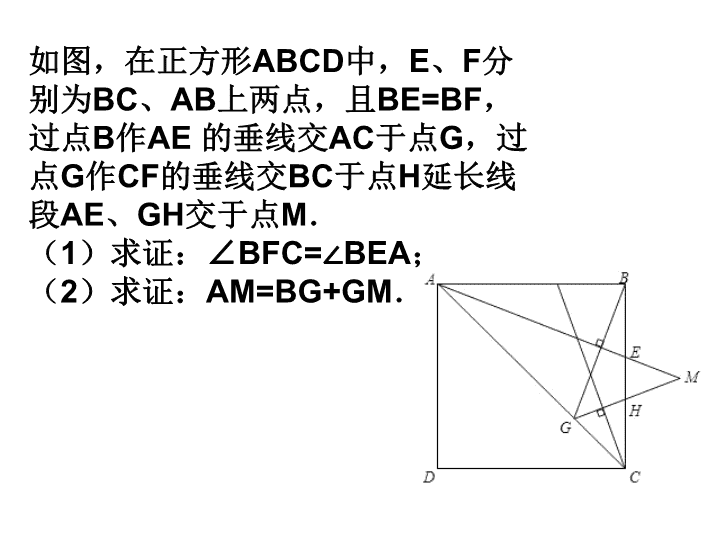
如图正方形ABCD中,E为AD边上的中点,过A作AF⊥BE,交CD边于F,M是AD边上一点,且有BM=DM+CD.⑴求证:点F是CD边的中点;⑵求证:∠MBC=2∠ABE.\n如图,在正方形ABCD中,E、F分别为BC、AB上两点,且BE=BF,过点B作AE的垂线交AC于点G,过点G作CF的垂线交BC于点H延长线段AE、GH交于点M.
(1)求证:∠BFC=∠BEA;
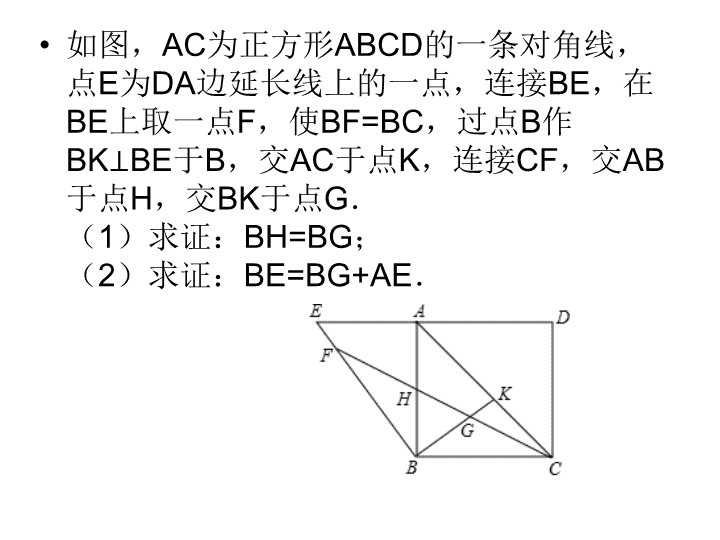
(2)求证:AM=BG+GM.\n如图,AC为正方形ABCD的一条对角线,点E为DA边延长线上的一点,连接BE,在BE上取一点F,使BF=BC,过点B作BK⊥BE于B,交AC于点K,连接CF,交AB于点H,交BK于点G.
(1)求证:BH=BG;
(2)求证:BE=BG+AE.\n如图,△ABC中,∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM⊥AC于点M,BM交CD于点E,且点E为CD的中点,连接MD,过点D作ND⊥MD于点D,DN交BM于点N.(1)若BC=,求△BDE的周长;(2)求证:NE-ME=CM.\n已知:如图,在正方形ABCD中,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F.(1)求证:∠DAE=∠DCE;(2)当CG=CE时,试判断CF与EG之间有怎样的数量关系?并证明你的结论.\n如图,点是矩形的边延长线上一点,连接,交于点是的中点,再连接、,且。(1)求证;(2)若,求的度数。\n如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG。求证:(1)AF=CG;(2)CF=2DE\n已知:如图,正方形ABCD中,点E是BA延长线上一点,连接DE,点F在DE上且DF=DC,DG⊥CF于G.DH平分∠ADE交CF于点H,连接BH.(1)若DG=2,求DH的长;(2)求证:BH+DH=CH.GHFACBDE\n如图,正方形ABCD中,P在对角线BD上,E在CB的延长线上,且PE=PC,过点P作PF⊥AE于F,直线PF分别交AB、CD于G、H,(1)求证:DH=AG+BE;(2)若BE=1,AB=3,求PE的长.\n如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.(1)求证:BE=CF;(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.\n如图,P是正方形ABCD内一点,连接PA、PB、PC,将△ABP绕点B顺时针旋转到△CBP′的位置.(1)旋转中心是点,点P旋转的度数是度;(2)连结PP′,求证:△BPP′是等腰直角三角形;(3)若PA=2,PB=4,∠APB=135°.①求△BPP′的周长;②求PC的长.\n已知:如图,在矩形中,是对角线.点为矩形外一点且满足,.交于点,连接,过点作交于.(1)若,求矩形的面积;(2)若,求证:\n\n如图,在□ABCD中,延长CD至点E,使DE=CD,连接BE交AD于点F,交AC于点G.(1)求证:AF=DF;(2)若BC=2AB,DE=1,∠ABC=60°,求FG的长.ABCDEFG\n\n如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D、E分别在AB、AC上且AD=AE,连接CD、BE,过点A作AF⊥BE交BC于F,过点F作FG⊥CD交CA于G.证明:(1)∠AFB=∠GFC(2)AE=CG\n已知:如图,在△ABC中,AB=AC,延长BC到D,使BD=2BC,连接AD,过C作CE⊥BD交AD于点E,连接BE交AC于点O.(1)求证:∠CAD=∠ABE.(2)求证:OA=OC\n如图,口ABCD中,E在AD边上,AE=DC,F为口ABCD外一点,连接AF、BF,连接EF交AB于G,且∠EFB=∠C=60°.(1)若AB=6,BC=8,求口ABCD的面积;(2)求证:EF=AF+BF.\n\n已知如图,在矩形ABCD中,E为CB延长线上一点,CE=AC,F是AE的中点.(1)求证:BF⊥DF;(2)若矩形ABCD的面积为48,且AB:AD=3:4,求DF的长.\n已知:正方形ABCD中,E是AB的中点,F是AD上一点,且ED=FC,ED、FC交于点G,连接BG,BH平分GBC交FC于H,连接DH。(1)求证:ED⊥FC;(2)求证:△DGH是等腰直角三角形\n如图,等边中,是的角平分线,上一点,以为一边且在下方作等边,连接。(1)求证:;(2)延长线上一点,连接。若的长。\n\n.已知:如图,四边形ABCD中AC、BD相于点D,AB=AC,,BD平分且于E,OA=1.(1)求OC的长;(2)求证:BO=2CD.\n\n如图所示,在正方形ABCD的边CB的延长线上取点F,连结AF,在AF上取点G,使得AG=AD,连结DG,过点A作AE⊥AF,交DG于点E.(1)若正方形ABCD的边长为4,且,求FG的长;(2)求证:AE+BF=AF.\n如图,□ABCD中,E是BC边的中点,连接AE,F为CD边上一点,且满足∠DFA=2∠BAE.(1)若∠D=105°,∠DAF=35°.求∠FAE的度数;(2)求证:AF=CD+CF.BD24题图EAFC\n\n\n\nACBDEFMN24题图\n\n\n如图,在△ABC中,AB=AC,EF为△ABC的中位线,点G为EF的中点,连接BG,CG.(1)求证:BG=CG;(2)当∠BGC=90°时,过点B作BD⊥AC,交GC于H,连接HF,求证:BH=FH+CF.24题图\n\n\n\n\n\n\n(24题图)\n在Rt△ABC中,∠BAC=90°,D为BC的中点,连接AD,E为AB上一点,过E作EF∥BC交AD于F.(1)求证:EF=AF.(2)若H为EC的中点,连接FH、DH,求证:DH⊥FH.\n24,如图,在平行四边形ABCD中,点E为边BC上一点,EF⊥AD于F,点G为AB的中点,∠BEG=∠CED求证:AF+BE=DF若GE=EF=1,求DF的长度\n\n\n如图1,点M、N分别是正方形ABCD的边AB、AD的中点,连接CN、DM.
(1)判断CN、DM的数量关系与位置关系,并说明理由;
(2)如图2,设CN、DM的交点为H,连接BH,求证:BH=BC;
(3)将△ADM沿DM翻折得到△A′DM,延长MA′交DC的延长线于点E,如图3,求cos∠DEM.\n如图,正方形ABCD中,E是AD的中点,F是AB边上的一点,连接FE并延长与CD的延长线相交于点G,作EH⊥FG交BC的延长线于点H.
(1)若BC=8,BF=5,求线段FG的长;
(2)求证:EH=2EG.\n\n\n\n\n谢谢!放映结束感谢各位批评指导!让我们共同进步