初中数学有关旋转的练习题 76页

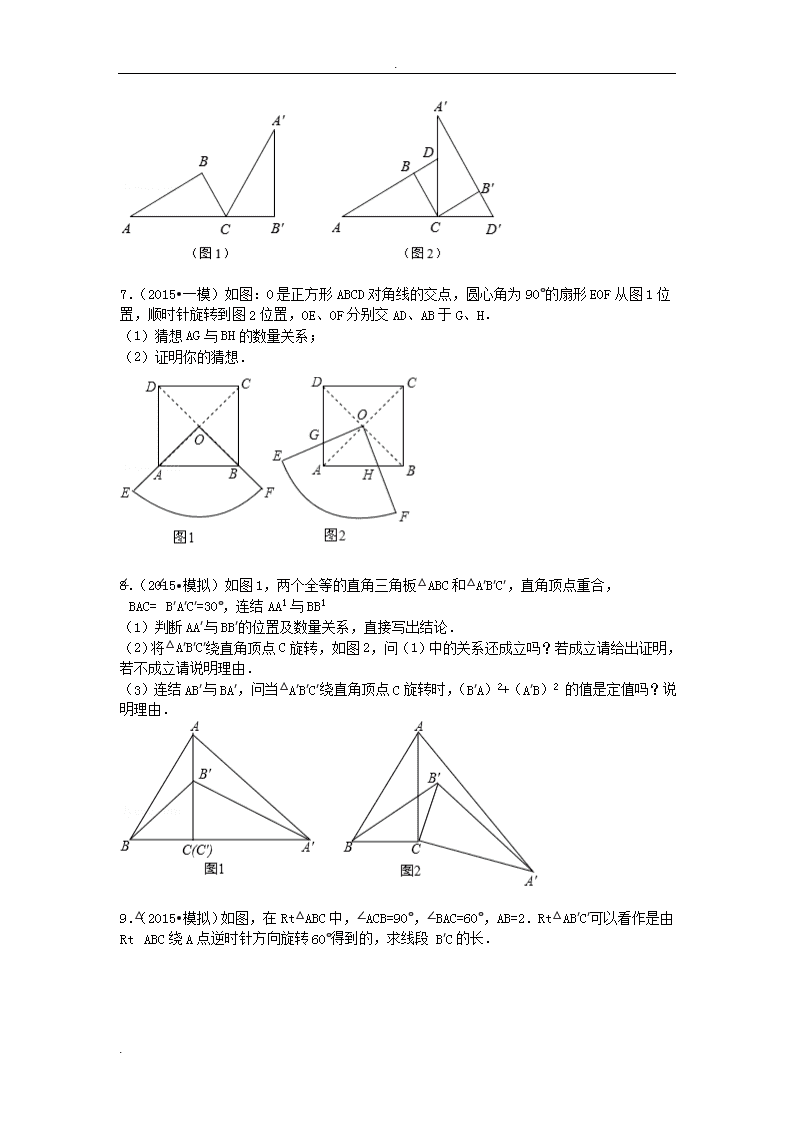
.2015年09月21日1148955744的初中数学组卷　一．解答题（共30小题）1．（2015•）如图，△ABC中，AB=AC=1，∠BAC=45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE、CF相交于点D．（1）求证：BE=CF；（2）当四边形ACDE为菱形时，求BD的长．　2．（2015•黄冈中学自主招生）阅读下面材料：小伟遇到这样一个问题：如图1，在△ABC（其中∠BAC是一个可以变化的角）中，AB=2，AC=4，以BC为边在BC的下方作等边△PBC，求AP的最大值．小伟是这样思考的：利用变换和等边三角形将边的位置重新组合．他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC，连接A′A，当点A落在A′C上时，此题可解（如图2）．请你回答：AP的最大值是　　　　　　．参考小伟同学思考问题的方法，解决下列问题：如图3，等腰Rt△ABC．边AB=4，P为△ABC部一点，则AP+BP+CP的最小值是　　　　　　．（结果可以不化简）　3．（2015•裕华区模拟）如图，点O是等边△ABC一点，∠AOB=110°，∠BOC=a．将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．（1）求证：△COD是等边三角形；（2）当a=150°时，试判断△AOD的形状，并说明理由；（3）探究：当a为多少度时，△AOD是等腰三角形？.\n.　4．（2015•新泰市校级模拟）如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转△ABF的位置．（1）旋转中心是点　　　　　　，旋转角度是　　　　　　度；（2）若连结EF，则△AEF是　　　　　　三角形；并证明；（3）若四边形AECF的面积为25，DE=2，求AE的长．　5．（2015•宝应县一模）已知：如图所示，△ABC为任意三角形，若将△ABC绕点C顺时针旋转180°得到△DEC．（1）试猜想AE与BD有何关系？并且直接写出答案．（2）若△ABC的面积为4cm2，求四边形ABDE的面积；（3）请给△ABC添加条件，使旋转得到的四边形ABDE为矩形，并说明理由．　6．（2015•惠山区二模）如图1，在△ABC中，∠B=90°，∠A=30°，AC=2．（1）将△ABC绕点C顺时针旋转120°得△A′B′C．①求点B旋转经过的路径长；②求线段BB′的长；（2）如图2，过点C作AC的垂线与AB的延长线交于点D，将△ACD绕点C顺时针旋转90°得△A′CD′．在图2中画出线段AD绕点C旋转所形成的图形（用阴影表示），并求出该图形的面积．.\n.　7．（2015•一模）如图：O是正方形ABCD对角线的交点，圆心角为90°的扇形EOF从图1位置，顺时针旋转到图2位置，OE、OF分别交AD、AB于G、H．（1）猜想AG与BH的数量关系；（2）证明你的猜想．　8．（2015•模拟）如图1，两个全等的直角三角板△ABC和△A′B′C′，直角顶点重合，∠BAC=∠B′A′C′=30°，连结AA1与BB1（1）判断AA′与BB′的位置及数量关系，直接写出结论．（2）将△A′B′C′绕直角顶点C旋转，如图2，问（1）中的关系还成立吗？若成立请给出证明，若不成立请说明理由．（3）连结AB′与BA′，问当△A′B′C′绕直角顶点C旋转时，（B′A）2+（A′B）2的值是定值吗？说明理由．　9．（2015•模拟）如图，在Rt△ABC中，∠ACB=90°，∠BAC=60°，AB=2．Rt△AB′C′可以看作是由Rt△ABC绕A点逆时针方向旋转60°得到的，求线段B′C的长．.\n.　10．（2015•燕山区一模）△ABC中，∠ABC=45°，AH⊥BC于点H，将△AHC绕点H逆时针旋转90°后，点C的对应点为点D，直线BD与直线AC交于点E，连接EH．（1）如图1，当∠BAC为锐角时，①求证：BE⊥AC；②求∠BEH的度数；（2）当∠BAC为钝角时，请依题意用实线补全图2，并用等式表示出线段EC，ED，EH之间的数量关系．　11．（2015•模拟）如图，△OBD中，OD=BD，△OBD绕点O逆时针旋转一定角度后得到△OAC，此时B，D，C三点正好在一条直线上，且点D是BC的中点．（1）求∠COD度数；（2）求证：四边形ODAC是菱形．　12．（2015•樊城区模拟）将两块大小相同的含30°角的直角三角板（∠BAC=∠B′A′C=30°）按图①方式放置，固定三角板A′B′C，然后将三角板ABC绕直角顶点C顺时针方向旋转（旋转角小于90°）至图②所示的位置，AB与A′C交于点E，AC与A′B′交于点F，AB与A′B′相交于点O．（1）当旋转角为　　　　　　度时，CF=CB′；（2）在上述条件下，AB与A′B′垂直吗？请说明理由．.\n.　13．（2015•模拟）如图，在正方形网络中，△ABC的三个顶点都在格点上，点A、B、C的坐标分别为（﹣2，4）、（﹣2，0）、（﹣4，1），将△ABC绕原点O旋转180度得到△A1B1C1．结合所给的平面直角坐标系解答下列问题：（1）画出△A1B1C1；（2）画出一个△A2B2C2，使它分别与△ABC，△A1B1C1轴对轴（其中点A，B，C与点A2，B2，C2对应）；（3）在（2）的条件下，若过点B的直线平分四边形ACC2A2的面积，请直接写出该直线的函数解析式．　14．（2014•模拟）如图，E是正方形ABCD申CD边上任意一点．（1）以点A为中心，把△ADE顺时针旋转90°，画出旋转后的图形；（2）在BC边上画一点F，使△CFE的周长等于正方形ABCD的周长的一半，请简要说明你取该点的理由．　15．（2015•模拟）在边长为1的小正方形网格中，△AOB的顶点均在格点上，.\n.（1）B点关于y轴的对称点坐标为　　　　　　；（2）将△AOB向左平移3个单位长度得到△A1O1B1，请画出△A1O1B1；（3）将△AOB以O为旋转中心顺时针旋转90°得到△A2OB2，求旋转过程中OA所扫过的面积．　16．（2013•顺庆区校级自主招生）如图，在梯形ABCD中，AB∥DC，∠ABC=90°，AB=2，BC=4，tan∠ADC=2．（1）求证：DC=BC；（2）E是梯形一点，连接DE、CE，将△DCE绕点C顺时针旋转90°，得△BCF，连接EF．判断EF与CE的数量关系，并证明你的结论；（3）在（2）的条件下，当CE=2BE，∠BEC=135°时，求cos∠BFE的值．　17．（2013•）在Rt△ABC中，∠C=90°，AC=1，BC=，点O为Rt△ABC一点，连接A0、BO、CO，且∠AOC=∠COB=BOA=120°，按下列要求画图（保留画图痕迹）：以点B为旋转中心，将△AOB绕点B顺时针方向旋转60°，得到△A′O′B（得到A、O的对应点分别为点A′、O′），并回答下列问题：∠ABC=　　　　　　，∠A′BC=　　　　　　，OA+OB+OC=　　　　　　．　.\n.18．（2013•）某校九年级学习小组在探究学习过程中，用两块完全相同的且含60°角的直角三角板ABC与AFE按如图（1）所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），如图（2），AE与BC交于点M，AC与EF交于点N，BC与EF交于点P．（1）求证：AM=AN；（2）当旋转角α=30°时，四边形ABPF是什么样的特殊四边形？并说明理由．　19．（2013•潍坊）如图1所示，将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起，构成一个大的长方形ABEF．现将小长方形CEFD绕点C顺时针旋转至CE′F′D′，旋转角为a．（1）当点D′恰好落在EF边上时，求旋转角a的值；（2）如图2，G为BC中点，且0°＜a＜90°，求证：GD′=E′D；（3）小长方形CEFD绕点C顺时针旋转一周的过程中，△DCD′与△CBD′能否全等？若能，直接写出旋转角a的值；若不能说明理由．　20．（2013•）如图1，在△ABC中，∠A=36°，AB=AC，∠ABC的平分线BE交AC于E．（1）求证：AE=BC；（2）如图（2），过点E作EF∥BC交AB于F，将△AEF绕点A逆时针旋转角α（0°＜α＜144°）得到△AE′F′，连结CE′，BF′，求证：CE′=BF′；（3）在（2）的旋转过程中是否存在CE′∥AB？若存在，求出相应的旋转角α；若不存在，请说明理由．.\n.　21．（2013•崇左）如图所示，正方形ABCD中，E是CD上一点，F在CB的延长线上，且DE=BF．（1）求证：△ADE≌△ABF；（2）问：将△ADE顺时针旋转多少度后与△ABF重合，旋转中心是什么？　22．（2014春•江都市校级月考）作图题：（1）作出四边形ABCD关于O点成中心对称的四边形A′B′C′D′（如图1）；（2）在如图的方格纸中，每个小方格都是边长为1个单位的正方形，△ABC的三个顶点都在格点上（每个小方格的顶点叫格点）．画出△ABC绕点O顺时针旋转90°后的△A1B1C1．（如图2）　23．（2014春•邵东县校级月考）如图，已知△ABC的三个顶点的坐标分别为A（﹣1，2）、B（﹣3，0）、C（0，0）．（1）请画出△ABC绕点A顺时针旋转90°的图形△AB1C1；.\n.（2）以C为位似中心，在x轴下方作△ABC的位似图形△A2B2C2，使△ABC放大，位似比为2：1，请画出图形，并求出△A2B2C的面积；（3）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标．　24．（2014秋•泰兴市校级月考）已知，如图▱ABCD中，AB⊥AC，AB=1，BC=，对角线AC、BD交于0点，将直线AC绕点0顺时针旋转，分别交BC、AD于点E、F（1）求证：AF=EC；（2）在旋转过程中，四边形BEDF可能是菱形吗？如果不能，请说明理由；如果能，说明理由并求出此时AC绕点0顺时针旋转的度数．　25．（2014秋•校级月考）已知：如图，点E是正方形ABCD的边AB上一点，点F是边BC上一点，且AE+CF=EF．求∠EDF的度数．　26．（2014春•永定县校级月考）如图，点E是正方形ABCD一点，连接AE、BE、CE，将△ABE绕点B顺时针旋转90°到△CBE的位置．若AE=1，BE=2，CE=3，则求∠BE′C的度数．（提示：连接EE′）.\n.　27．（2014春•涟水县校级月考）如图，在Rt△ABC中，∠ACB=90°，∠A=20°，将△ABC绕点C按顺时针方向旋转后得到△EDC，此时点D在AB边上，求旋转角的大小．　28．（2014秋•明山区校级月考）如图，已知△BAD≌△BCE，∠BAD=∠BCE=90°，∠ABD=∠BEC=30°，点M为DE的中点，过点E与AD平行的直线交射线AM于点N．（1）如图1，当A，B，E三点在同一直线上时，判断AC与CN数量关系为　　　　　　；（2）将图1中△BCE绕点B逆时针旋转到图2位置时，（1）中的结论是否仍成立？若成立，试证明之，若不成立，请说明理由；（3）将图1中△BCE绕点B逆时针旋转一周，旋转过程中△CAN能否为等腰直角三角形？若能，直接写出旋转角度；若不能，说明理由．　29．（2014秋•闽侯县校级月考）如图，在平面直角坐标系中，已知△AOB是等边三角形，点A的坐标是（0，3），点B在第一象限，∠OAB的平分线交x轴于点P，把△AOP绕着点A按逆时针方向旋转，使边AO与AB重合，得到△ABD，连接DP．求：DP的长及点D的坐标．.\n.　30．（2014春•泰兴市校级月考）如图①，两个全等的等腰直角△ABC和△EDC中，∠ACB=∠ECD=90°，点A与点E重合，点D与点B重合．现△ABC不动，把△EDC绕点C按顺时针方向旋转，旋转角为α（0°＜α＜90°）．（1）如图②，AB与CE交于F，ED与AB、BC分别交于M、H．求证：CF=CH；（2）如图③，当α=45°时，试判断四边形ACDM是什么四边形，并说明理由；（3）如图②，在△EDC绕点C旋转的过程中，连接BD，当旋转角α的度数为　　　　　　时，△BDH是等腰三角形．　　.\n.2015年09月21日1148955744的初中数学组卷参考答案与试题解析　一．解答题（共30小题）1．（2015•）如图，△ABC中，AB=AC=1，∠BAC=45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE、CF相交于点D．（1）求证：BE=CF；（2）当四边形ACDE为菱形时，求BD的长．考点：旋转的性质；勾股定理；菱形的性质．菁优网所有专题：计算题；证明题．分析：（1）先由旋转的性质得AE=AB，AF=AC，∠EAF=∠BAC，则∠EAF+∠BAF=∠BAC+∠BAF，即∠EAB=∠FAC，利用AB=AC可得AE=AF，于是根据旋转的定义，△AEB可由△AFC绕点A按顺时针方向旋转得到，然后根据旋转的性质得到BE=CD；.\n.（2）由菱形的性质得到DE=AE=AC=AB=1，AC∥DE，根据等腰三角形的性质得∠AEB=∠ABE，根据平行线得性质得∠ABE=∠BAC=45°，所以∠AEB=∠ABE=45°，于是可判断△ABE为等腰直角三角形，所以BE=AC=，于是利用BD=BE﹣DE求解．解答：（1）证明：∵△AEF是由△ABC绕点A按顺时针方向旋转得到的，∴AE=AB，AF=AC，∠EAF=∠BAC，∴∠EAF+∠BAF=∠BAC+∠BAF，即∠EAB=∠FAC，∵AB=AC，∴AE=AF，∴△AEB可由△AFC绕点A按顺时针方向旋转得到，∴BE=CF；（2）解：∵四边形ACDE为菱形，AB=AC=1，∴DE=AE=AC=AB=1，AC∥DE，∴∠AEB=∠ABE，∠ABE=∠BAC=45°，∴∠AEB=∠ABE=45°，∴△ABE为等腰直角三角形，∴BE=AC=，∴BD=BE﹣DE=﹣1．.\n.点评：本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了菱形的性质．　2．（2015•黄冈中学自主招生）阅读下面材料：小伟遇到这样一个问题：如图1，在△ABC（其中∠BAC是一个可以变化的角）中，AB=2，AC=4，以BC为边在BC的下方作等边△PBC，求AP的最大值．小伟是这样思考的：利用变换和等边三角形将边的位置重新组合．他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC，连接A′A，当点A落在A′C上时，此题可解（如图2）．请你回答：AP的最大值是　6　．参考小伟同学思考问题的方法，解决下列问题：如图3，等腰Rt△ABC．边AB=4，P为△ABC部一点，则AP+BP+CP的最小值是　（或不化简为）　．（结果可以不化简）考点：旋转的性质；全等三角形的判定与性质；等边三角形的性质；勾股定理；等腰直角三角形．菁优网所有专题：几何综合题．分析：.\n.（1）根据旋转的性质知A′A=AB=BA′=2，AP=A′C，所以在△AA′C中，利用三角形三边关系来求A′C即AP的长度；（2）以B为中心，将△APB逆时针旋转60°得到△A'P'B．根据旋转的性质推知PA+PB+PC=P'A′+P'B+PC．当A'、P'、P、C四点共线时，（P'A′+P'B+PC）最短，即线段A'C最短．然后通过作辅助线构造直角三角形A′DC，在该直角三角形利用勾股定理来求线段A′C的长度．解答：解：（1）如图2，∵△ABP逆时针旋转60°得到△A′BC，∴∠A′BA=60°，A′B=AB，AP=A′C∴△A′BA是等边三角形，∴A′A=AB=BA′=2，在△AA′C中，A′C＜AA′+AC，即AP＜6，则当点A′A、C三点共线时，A′C=AA′+AC，即AP=6，即AP的最大值是：6；故答案是：6．.\n.（2）如图3，∵Rt△ABC是等腰三角形，∴AB=BC．以B为中心，将△APB逆时针旋转60°得到△A'P'B．则A'B=AB=BC=4，PA=P′A′，PB=P′B，∴PA+PB+PC=P′A′+P'B+PC．∵当A'、P'、P、C四点共线时，（P'A+P'B+PC）最短，即线段A'C最短，∴A'C=PA+PB+PC，∴A'C长度即为所求．过A'作A'D⊥CB延长线于D．∵∠A'BA=60°（由旋转可知），∴∠1=30°．∵A'B=4，∴A'D=2，BD=2，∴CD=4+2．在Rt△A'DC中A'C====2+2；∴AP+BP+CP的最小值是：2+2（或不化简为）．故答案是：2+2（或不化简为）．.\n.点评：本题综合考查了旋转的性质、等腰直角三角形的性质、勾股定理以及等边三角形的判定与性质．注意：旋转前、后的图形全等．　3．（2015•裕华区模拟）如图，点O是等边△ABC一点，∠AOB=110°，∠BOC=a．将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．（1）求证：△COD是等边三角形；（2）当a=150°时，试判断△AOD的形状，并说明理由；（3）探究：当a为多少度时，△AOD是等腰三角形？考点：.\n.旋转的性质；全等三角形的判定与性质；等腰三角形的判定；等边三角形的判定与性质．菁优网所有专题：几何综合题．分析：（1）根据旋转的性质可得出OC=OD，结合题意即可证得结论；（2）结合（1）的结论可作出判断；（3）找到变化中的不变量，然后利用旋转及全等的性质即可做出解答．解答：（1）证明：∵将△BOC绕点C按顺时针方向旋转60°得△ADC，∴CO=CD，∠OCD=60°，∴△COD是等边三角形．（2）解：当α=150°时，△AOD是直角三角形．理由是：∵将△BOC绕点C按顺时针方向旋转60°得△ADC，∴△BOC≌△ADC，∴∠ADC=∠BOC=150°，又∵△COD是等边三角形，∴∠ODC=60°，∴∠ADO=∠ADC﹣∠ODC=90°，∵∠α=150°∠AOB=110°，∠COD=60°，.\n.∴∠AOD=360°﹣∠α﹣∠AOB﹣∠COD=360°﹣150°﹣110°﹣60°=40°，∴△AOD不是等腰直角三角形，即△AOD是直角三角形．（3）解：①要使AO=AD，需∠AOD=∠ADO，∵∠AOD=360°﹣110°﹣60°﹣α=190°﹣α，∠ADO=α﹣60°，∴190°﹣α=α﹣60°，∴α=125°；②要使OA=OD，需∠OAD=∠ADO．∵∠OAD=180°﹣（∠AOD+∠ADO）=180°﹣（190°﹣α+α﹣60°）=50°，∴α﹣60°=50°，∴α=110°；③要使OD=AD，需∠OAD=∠AOD．∵∠OAD=360°﹣110°﹣60°﹣α=190°﹣α，∠AOD==120°﹣，∴190°﹣α=120°﹣，解得α=140°．.\n.综上所述：当α的度数为125°或110°或140°时，△AOD是等腰三角形．点评：本题以“空间与图形”中的核心知识（如等边三角形的性质、全等三角形的性质与证明、直角三角形的判定、多边形角和等）为载体，容由浅入深，层层递进．试题中几何演绎推理的难度适宜，蕴含着丰富的思想方法（如运动变化、数形结合、分类讨论、方程思想等），能较好地考查学生的推理、探究及解决问题的能力．　4．（2015•新泰市校级模拟）如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转△ABF的位置．（1）旋转中心是点　A　，旋转角度是　90　度；（2）若连结EF，则△AEF是　等腰直角　三角形；并证明；（3）若四边形AECF的面积为25，DE=2，求AE的长．考点：旋转的性质．菁优网所有分析：（1）根据旋转变换的定义，即可解决问题．（2））根据旋转变换的定义，即可解决问题．.\n.（3）根据旋转变换的定义得到△ADE≌△ABF，进而得到S四边形AECF=S正方形ABCD=25，求出AD的长度，即可解决问题．解答：解：（1）如图，由题意得：旋转中心是点A，旋转角度是90度．故答案为A、90．（2）由题意得：AF=AE，∠EAF=90°，∴△AEF为等腰直角三角形．故答案为等腰直角．（3）由题意得：△ADE≌△ABF，∴S四边形AECF=S正方形ABCD=25，∴AD=5，而∠D=90°，DE=2，∴．点评：.\n.该题主要考查了旋转变换的性质、正方形的性质、勾股定理等几何知识点及其应用问题；解题的关键是牢固掌握旋转变换的性质、正方形的性质、勾股定理等几何知识，这是灵活运用、解题的基础和关键．　5．（2015•宝应县一模）已知：如图所示，△ABC为任意三角形，若将△ABC绕点C顺时针旋转180°得到△DEC．（1）试猜想AE与BD有何关系？并且直接写出答案．（2）若△ABC的面积为4cm2，求四边形ABDE的面积；（3）请给△ABC添加条件，使旋转得到的四边形ABDE为矩形，并说明理由．考点：旋转的性质；矩形的判定．菁优网所有分析：（1）易证四边形ABDE是平行四边形，根据平行四边形的性质即可求解；（2）根据平行四边形的性质：平行四边形的对角线互相平分，即可得到平行四边形的面积是△ABC的面积的四倍，据此即可求解；（3）四边形ABDE是平行四边形，只要有条件：对角线相等即可得到四边形ABDE是矩形．解答：解：（1）AE∥BD，且AE=BD；.\n.（2）四边形ABDE的面积是：4×4=16；（3）AC=BC．理由是：∵AC=CD，BC=CE，∴四边形ABDE是平行四边形．∵AC=BC，∴平行四边形ABDE是矩形．点评：本题考查了图形的旋转以及平行四边形的判定与性质以及矩形的判定方法，正确理解四边形ABDE是平行四边形是关键．　6．（2015•惠山区二模）如图1，在△ABC中，∠B=90°，∠A=30°，AC=2．（1）将△ABC绕点C顺时针旋转120°得△A′B′C．①求点B旋转经过的路径长；②求线段BB′的长；（2）如图2，过点C作AC的垂线与AB的延长线交于点D，将△ACD绕点C顺时针旋转90°得△A′CD′．在图2中画出线段AD绕点C旋转所形成的图形（用阴影表示），并求出该图形的面积．考点：旋转的性质．菁优网所有分析：.\n.（1）①由旋转的性质可知∠BCB′=120°，然后由扇形的弧长公式即可求得点B旋转经过的路径长；②由特殊锐角三角函数值可求得BB′的长；（2）首先画出图形，然后根据S1=S2，可求得S1+S4的面积，然后再利用扇形面积﹣等边三角形ECD′的面积，从而可求得答案．解答：解：（1）①∵AC=2，∠B=90°，∠A=30°，∴BC=1．∴点B旋转的路径==π；…（2分）②如下图所示：在△BCB′中，CB=CB′，∠BCB′=120°，AC⊥BB′∴sin∠CBE==．∴BE=．∴BB′=；…（4分）（2）如图所示：.\n.…（5分）∵S1=S2，∴S2+S4=S1+S4=π（AC2﹣BC2）==．在Rt△ABD中，DC=AC•tan30°=，S3=﹣=，∴S2+S3+S4==．…（8分）点评：本题主要考查的是旋转的性质，根据旋转的性质画出图形，然后根据S1=S2，求得S2+S4是解题的关键．　.\n.7．（2015•一模）如图：O是正方形ABCD对角线的交点，圆心角为90°的扇形EOF从图1位置，顺时针旋转到图2位置，OE、OF分别交AD、AB于G、H．（1）猜想AG与BH的数量关系；（2）证明你的猜想．考点：旋转的性质；全等三角形的判定与性质；正方形的性质．菁优网所有分析：（1）观察图形，容易发现AG=BH．（2）首先证明∠OAG=∠OBH=45°，OA=OB；进而证明△AOG≌△BOH，即可解决问题．解答：解：如图，（1）AG=BH．（2）∵四边形ABCD为正方形，∴∠OAG=∠OBH=45°，OA=OB，∠AOB=90°；由题意得：∠GOH=90°，∴∠AOG=∠BOH；在△AOG与△BOH中，，∴△AOG≌△BOH（ASA），.\n.∴AG=BH．点评：该题以正方形为载体，以考查正方形的性质、全等三角形的判定、旋转变换的性质等几何知识点为核心构造而成；牢固掌握正方形的性质等几何知识点是基础，灵活运用是关键．　8．（2015•模拟）如图1，两个全等的直角三角板△ABC和△A′B′C′，直角顶点重合，∠BAC=∠B′A′C′=30°，连结AA1与BB1（1）判断AA′与BB′的位置及数量关系，直接写出结论．（2）将△A′B′C′绕直角顶点C旋转，如图2，问（1）中的关系还成立吗？若成立请给出证明，若不成立请说明理由．（3）连结AB′与BA′，问当△A′B′C′绕直角顶点C旋转时，（B′A）2+（A′B）2的值是定值吗？说明理由．考点：旋转的性质；勾股定理．菁优网所有分析：.\n.（1）根据题意结合已知图形可以猜测：AA′⊥B′B且；（2）如图，作辅助线；首先运用旋转变换的性质，结合三角形的角和定理证明AA′⊥BB′；其次证明△CAA′∽△CBB′，得到，运用相似三角形的性质求出，即可解决问题；（3）运用（2）中的结论，结合勾股定理，即可解决问题．解答：解：（1）AA′⊥B′B且；（2）（1）中的结论仍成立，证明如下：如图，设BB′的延长线与AA′交于点M，设∠ACB′=α，由题意得：∠BCB′=∠ACA′=90°+α，∵BC=B′C，AC=A′C，∴∠CBO=∠OAD==45°﹣，.\n.∵∠CBO+∠BOC=90°，而∠BOC=∠AOD，∴∠OAD+∠AOD=90°，∴OD⊥AA′，即AA′⊥BB′；由题意知：∠ACA′=∠BCB′，CA=CA′，CB=CB′，∴，∴△CAA′∽△CBB′，∴，在直角三角形ABC中，∵∠BAC=30°，∴，∴，即（1）中的结论仍成立；（3）是定值；由（2）知：OD⊥AA′；∴B′A2+A′B2=B′D2+AD2+BD2+A′D2=B′D2+A′D2+BD2+AD2=AB2+（A′B′）2=2AB2，∴B′A2+A′B2是定值．点评：.\n.本题主要考查了旋转变换的性质、勾股定理等几何知识点及其应用问题，牢固掌握旋转变换的性质、勾股定理等几何知识点是解答此题的关键．　9．（2015•模拟）如图，在Rt△ABC中，∠ACB=90°，∠BAC=60°，AB=2．Rt△AB′C′可以看作是由Rt△ABC绕A点逆时针方向旋转60°得到的，求线段B′C的长．考点：旋转的性质．菁优网所有专题：计算题．分析：如图，作B′E⊥AC交CA的延长线于E，利用含30度的直角三角形三边的关系得AC=AB=1，再根据旋转的性质得AB=AB′=2，∠B′AB=60°，则∠EAB′=180°﹣∠B′AB﹣∠BAC=60°，可计算出∠AB′E=30°，所以AE=1，在Rt△AB′E中利用勾股定理可计算出B′E=.\n.，则EC=AE+AC=2，然后在Rt△CEB′中根据勾股定理可计算出B′C=．解答：解：如图，作B′E⊥AC交CA的延长线于E，∵∠ACB=90°，∠BAC=60°，AB=2，∴∠ABC=30°，∴AC=AB=1，∵Rt△AB′C′可以看作是由Rt△ABC绕点A逆时针方向旋转60°得到的，∴AB=AB′=2，∠B′AB=60°，∴∠EAB′=180°﹣∠B′AB﹣∠BAC=60°，∵B′E⊥EC，∴∠AB′E=30°，∴AE=1，在Rt△AB′E中，∵AE=1，AB′=2，∴B′E==，∴EC=AE+AC=2，在Rt△CEB′中，∵B′E=，CE=2，∴B′C==．点评：.\n.本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了勾股定理．　10．（2015•燕山区一模）△ABC中，∠ABC=45°，AH⊥BC于点H，将△AHC绕点H逆时针旋转90°后，点C的对应点为点D，直线BD与直线AC交于点E，连接EH．（1）如图1，当∠BAC为锐角时，①求证：BE⊥AC；②求∠BEH的度数；（2）当∠BAC为钝角时，请依题意用实线补全图2，并用等式表示出线段EC，ED，EH之间的数量关系．考点：旋转的性质；全等三角形的判定与性质．菁优网所有分析：（1）由AH⊥BC于点H，∠ABC=45°，得到△ABH为等腰直角三角形，所以AH=BH，∠BAH=45°，由旋转性质得到△BHD≌△AHC，得到∠1=∠2，根据∠1+∠C=90°，得到∠2+∠C=90°，所以∠BEC=90°，即BE⊥AC，②由四点共圆即可得到结论；.\n.（2）过H作HF⊥EH交CE于F，由旋转的性质得：∠D=∠C，HD=CH，∠CHD=90°，证出三角形全等，得到CF=DE，HF=EH，即可得到结论．解答：（1）①证明：∵AH⊥BC于点H，∠ABC=45°，∴△ABH为等腰直角三角形，∴AH=BH，∠BAH=45°，∴△AHC绕点H逆时针旋转90°得△BHD，由旋转性质得，△BHD≌△AHC，∴∠1=∠2．∵∠1+∠C=90°，∴∠2+∠C=90°，∴∠BEC=90°，即BE⊥AC．②如图1，∵∠AHB=∠AEB=90°，∴A，B，H，E四点均在以AB为直径的圆上，∴∠BEH=∠BAH=45°，（2）解：补全图2，如图2；EC﹣ED=EH，过H作HF⊥EH交CE于F，由旋转的性质得：∠D=∠C，HD=CH，∠CHD=90°，.\n.∴∠EHD=∠CHF，在△DEH与△CFH中，，∴△DEH≌△CFH，∴CF=DE，HF=EH，∴EF=EH，∴CE﹣EF=CE﹣EH=CF=DE，∴EC﹣ED=EH．点评：本题考查了旋转的性质，全等三角形的判定与性质，四点共圆，正确的画出图形是解题的关键．　11．（2015•模拟）如图，△OBD中，OD=BD，△OBD绕点O逆时针旋转一定角度后得到△OAC，此时B，D，C三点正好在一条直线上，且点D是BC的中点．（1）求∠COD度数；（2）求证：四边形ODAC是菱形．.\n.考点：旋转的性质；菱形的判定．菁优网所有分析：（1）如图，根据题意证明△OBC为直角三角形，结合OC=，求出∠B即可解决问题．（2）首先证明AC∥OD，结合AC=OD，判断四边形ADOC为平行四边形，根据菱形的定义即可解决问题．解答：解：（1）如图，由题意得：OC=OD=BD；∵点D是BC的中点，∴CD=BD，OD=BC，∴△OBC为直角三角形，而OC=，∴∠B=30°，∠OCD=90°﹣30°=60°，；∵OD=CD，∴∠COD=∠OCD=60°．（2）∵OD=BD，∴∠DOB=∠B=30°，.\n.由旋转变换的性质知：∠COA=∠CAO=∠B=30°，∴∠AOD=90°﹣2×30°=30°，∴∠CAO=∠AOD=30°，∴AC∥OD，而AC=OD，∴四边形ADOC为平行四边形，而OC=OD，∴四边形ODAC是菱形．点评：该题主要考查了旋转变换的性质、直角三角形的判定、菱形的判定等几何知识点及其应用问题；解题的关键是牢固掌握旋转变换的性质、直角三角形的判定、菱形的判定等几何知识点，并能灵活运用．　12．（2015•樊城区模拟）将两块大小相同的含30°角的直角三角板（∠BAC=∠B′A′C=30°）按图①方式放置，固定三角板A′B′C，然后将三角板ABC绕直角顶点C顺时针方向旋转（旋转角小于90°）至图②所示的位置，AB与A′C交于点E，AC与A′B′交于点F，AB与A′B′相交于点O．（1）当旋转角为　30　度时，CF=CB′；（2）在上述条件下，AB与A′B′垂直吗？请说明理由．.\n.考点：旋转的性质．菁优网所有分析：（1）由CF=CB′可知∠CFB′=∠CB′F=60°，从而可求得∠FCB′的度数，然后可求得∠A′CA=30°；（2）由∠A′CA=30°，可求得∠ECB=60°，然后可求得∠A′EO=∠BEC=60°，从而可求得∠A′OE=90°．解答：解：（1）∵CF=CB′，∴∠CFB′=∠CB′F=60°．∴∠A′CA=90°﹣∠FCB′=90°﹣60°=30°．故旋转角为30°时，CF=CB′；故答案为：30°．（2）∵∠A′CA=30°，∴∠BCE=∠ACB﹣∠A′CA=90°﹣30°=60°．∴∠B=∠BCE=∠BEC=60°．∴∠A′EO=60°．.\n.∴∠A′EO+∠A′=60°+30°=90°．∴∠A′OE=90°．∴AB⊥A′B′．点评：本题主要考查的是旋转的性质和等边三角形的性质和判定，判定出△BCE和△B′CF为等边三角形是解题的关键．　13．（2015•模拟）如图，在正方形网络中，△ABC的三个顶点都在格点上，点A、B、C的坐标分别为（﹣2，4）、（﹣2，0）、（﹣4，1），将△ABC绕原点O旋转180度得到△A1B1C1．结合所给的平面直角坐标系解答下列问题：（1）画出△A1B1C1；（2）画出一个△A2B2C2，使它分别与△ABC，△A1B1C1轴对轴（其中点A，B，C与点A2，B2，C2对应）；（3）在（2）的条件下，若过点B的直线平分四边形ACC2A2的面积，请直接写出该直线的函数解析式．考点：作图-旋转变换；作图-轴对称变换．菁优网所有分析：（1）首先由旋转的性质求得对应点的坐标，然后画出图形即可；.\n.（2）由轴对称图形的性质找出对应点的坐标，然后画出图形即可；（3）分别画出三角形关于x轴对称和关于y轴对称的图形，然后再找出过点B平分四边形面积的直线，最后求得解析式即可．解答：解：（1）如图1所示：（2）如图1所示：直线解解析式为y=0；如图2所示：.\n.经过点B和（0，2.5）的直线平分四边形ACC2A2的面积，设直线的解析式为y=kx+b，将（﹣2，0）和（0，2.5）代入得：，解得：直线的解析式为y=．综上所述：直线的解析式为y=0或y=．点评：本题主要考查的是旋转变换、轴对称变换以及求一次函数的表达式，掌握旋转、轴对称的性质是解题的关键．　14．（2014•模拟）如图，E是正方形ABCD申CD边上任意一点．（1）以点A为中心，把△ADE顺时针旋转90°，画出旋转后的图形；（2）在BC边上画一点F，使△CFE的周长等于正方形ABCD的周长的一半，请简要说明你取该点的理由．考点：作图-旋转变换．菁优网所有.\n.分析：（1）利用旋转的性质得出△ABE′的位置；（2）根据全等三角形的判定与性质得出△AEF≌△AE′F（SAS），以及EF=E′F=BF+DE，进而得出EF+EC+FC=BC+CD．解答：解：（1）如图所示：△ABE′即为所求；（2）作∠EAE′的平分线交BC于点F，则△CFE的周长等于正方形ABCD的周长的一半，在△AEF和△AE′F中∵，∴△AEF≌△AE′F（SAS），∴EF=E′F=BF+DE，∴EF+EC+FC=BC+CD．点评：.\n.此题主要考查了图形的转变换以及全等三角形的判定与性质，得出△AEF≌△AE′F是解题关键．　15．（2015•模拟）在边长为1的小正方形网格中，△AOB的顶点均在格点上，（1）B点关于y轴的对称点坐标为　（﹣3，2）　；（2）将△AOB向左平移3个单位长度得到△A1O1B1，请画出△A1O1B1；（3）将△AOB以O为旋转中心顺时针旋转90°得到△A2OB2，求旋转过程中OA所扫过的面积．考点：作图-旋转变换；作图-平移变换．菁优网所有分析：（1）直接根据关于y轴对称轴坐标点的特征进行填空即可；（2）根据题意画出图形；（3）根据扇形的面积计算公式计算即可．解答：解：（1）根据图可知：点B坐标为（3，2），由于B点关于y轴对称，纵坐标不变，横坐标变为相反数，可知B点关于y轴的对称点坐标为（﹣3，2），.\n.故答案为（﹣3，2）；（2）作图如图1：（3）作图如图2，OA==，旋转过程中OA所扫过的面积S==．点评：.\n.本题主要考查了作图﹣平移变换和旋转变换的知识，解答本题的关键是正确地画出图形，熟练地掌握扇形面积公式，此题难度不大．　16．（2013•顺庆区校级自主招生）如图，在梯形ABCD中，AB∥DC，∠ABC=90°，AB=2，BC=4，tan∠ADC=2．（1）求证：DC=BC；（2）E是梯形一点，连接DE、CE，将△DCE绕点C顺时针旋转90°，得△BCF，连接EF．判断EF与CE的数量关系，并证明你的结论；（3）在（2）的条件下，当CE=2BE，∠BEC=135°时，求cos∠BFE的值．考点：旋转的性质；勾股定理；矩形的判定与性质；梯形；锐角三角函数的定义．菁优网所有专题：综合题．分析：（1）如图，过A作AP⊥DC于点P，由AB∥CD可以得到∠ABC=90°，然后得到四边形APCB是矩形，接着利用已知条件可以求出PC=AB=2，AP=BC=4，又在Rt△ADP中，根据tan∠ADC=可以求出DP=2，接着得到DC=4，由此即可解决问题；（2）EF=.\n.CE．由△DCE绕点C顺时针旋转90°得△BCF，根据旋转的性质得到CF=CE，∠ECF=90°，然后利用勾股定理即可求出EF；（3）由（2）得∠CEF=45°，而∠BEC=135°，由此得到∠BEF=90°．设BE=a，则CE=2a，由EF=CE，则EF=．在Rt△BEF中，由勾股定理得：BF=3a，然后根据余弦的定义即可求解．解答：解：（1）证明：作AP⊥DC于点P．∵AB∥CD，∠ABC=90°，∴四边形APCB是矩形，∴PC=AB=2，AP=BC=4．在Rt△ADP中，tan∠ADC=即=2，∴DP=2，∴DC=DP+PC=4=BC．（2）EF=CE．.\n.证明如下：由△DCE绕点C顺时针旋转90°得△BCF，∴CF=CE，∠ECF=90°，∴EF=．（3）由（2）得∠CEF=45°．∵∠BEC=135°，∴∠BEF=90°．设BE=a，则CE=2a，由EF=CE，则EF=在Rt△BEF中，由勾股定理得：BF=3a，∴cos∠BFE=．点评：此题分别考查了旋转的性质、勾股定理、矩形的性质、梯形的性质及三角函数的定义，综合性比较强，要求学生熟练掌握相关的基础知识才能很好解决这类问题．　.\n.17．（2013•）在Rt△ABC中，∠C=90°，AC=1，BC=，点O为Rt△ABC一点，连接A0、BO、CO，且∠AOC=∠COB=BOA=120°，按下列要求画图（保留画图痕迹）：以点B为旋转中心，将△AOB绕点B顺时针方向旋转60°，得到△A′O′B（得到A、O的对应点分别为点A′、O′），并回答下列问题：∠ABC=　30°　，∠A′BC=　90°　，OA+OB+OC=　　．考点：作图-旋转变换．菁优网所有专题：作图题；压轴题．分析：解直角三角形求出∠ABC=30°，然后过点B作BC的垂线，在截取A′B=AB，再以点A′为圆心，以AO为半径画弧，以点B为圆心，以BO为半径画弧，两弧相交于点O′，连接A′O′、BO′，即可得到△A′O′B；根据旋转角与∠ABC的度数，相加即可得到∠A′BC；.\n.根据直角三角形30°角所对的直角边等于斜边的一半求出AB=2AC，即A′B的长，再根据旋转的性质求出△BOO′是等边三角形，根据等边三角形的三条边都相等可得BO=OO′，等边三角形三个角都是60°求出∠BOO′=∠BO′O=60°，然后求出C、O、A′、O′四点共线，再利用勾股定理列式求出A′C，从而得到OA+OB+OC=A′C．解答：解：∵∠C=90°，AC=1，BC=，∴tan∠ABC===，∴∠ABC=30°，∵△AOB绕点B顺时针方向旋转60°，∴△A′O′B如图所示；∠A′BC=∠ABC+60°=30°+60°=90°，∵∠C=90°，AC=1，∠ABC=30°，∴AB=2AC=2，∵△AOB绕点B顺时针方向旋转60°，得到△A′O′B，∴A′B=AB=2，BO=BO′，A′O′=AO，∴△BOO′是等边三角形，∴BO=OO′，∠BOO′=∠BO′O=60°，∵∠AOC=∠COB=∠BOA=120°，∴∠COB+∠BOO′=∠BO′A′+∠BO′O=120°+60°=180°，.\n.∴C、O、A′、O′四点共线，在Rt△A′BC中，A′C===，∴OA+OB+OC=A′O′+OO′+OC=A′C=．故答案为：30°；90°；．点评：本题考查了利用旋转变换作图，旋转变换的性质，直角三角形30°角所对的直角边等于斜边的一半的性质，勾股定理，等边三角形的判定与性质，综合性较强，最后一问求出C、O、A′、O′四点共线是解题的关键．　18．（2013•）某校九年级学习小组在探究学习过程中，用两块完全相同的且含60°角的直角三角板ABC与AFE按如图（1）所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），如图（2），AE与BC交于点M，AC与EF交于点N，BC与EF交于点P．（1）求证：AM=AN；.\n.（2）当旋转角α=30°时，四边形ABPF是什么样的特殊四边形？并说明理由．考点：旋转的性质；全等三角形的判定与性质；菱形的判定．菁优网所有专题：压轴题．分析：（1）根据旋转的性质得出AB=AF，∠BAM=∠FAN，进而得出△ABM≌△AFN得出答案即可；（2）利用旋转的性质得出∠FAB=120°，∠FPC=∠B=60°，即可得出四边形ABPF是平行四边形，再利用菱形的判定得出答案．解答：（1）证明：∵用两块完全相同的且含60°角的直角三角板ABC与AFE按如图（1）所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），.\n.∴AB=AF，∠BAM=∠FAN，在△ABM和△AFN中，，∴△ABM≌△AFN（ASA），∴AM=AN；（2）解：当旋转角α=30°时，四边形ABPF是菱形．理由：连接AP，∵∠α=30°，∴∠FAN=30°，∴∠FAB=120°，∵∠B=60°，∴∠B+∠FAB=180°，∴AF∥BP，∴∠F=∠FPC=60°，∴∠FPC=∠B=60°，∴AB∥FP，∴四边形ABPF是平行四边形，∵AB=AF，∴平行四边形ABPF是菱形．点评：.\n.此题主要考查了平行四边形的判定以及菱形的判定和全等三角形的判定等知识，根据旋转前后图形大小不发生变化得出是解题关键．　19．（2013•潍坊）如图1所示，将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起，构成一个大的长方形ABEF．现将小长方形CEFD绕点C顺时针旋转至CE′F′D′，旋转角为a．（1）当点D′恰好落在EF边上时，求旋转角a的值；（2）如图2，G为BC中点，且0°＜a＜90°，求证：GD′=E′D；（3）小长方形CEFD绕点C顺时针旋转一周的过程中，△DCD′与△CBD′能否全等？若能，直接写出旋转角a的值；若不能说明理由．考点：旋转的性质；全等三角形的判定与性质；矩形的性质；正方形的性质．菁优网所有专题：计算题．分析：（1）根据旋转的性质得CD′=CD=2，在Rt△CED′中，CD′=2，CE=1，则∠CD′E=30°，然后根据平行线的性质即可得到∠α=30°；.\n.（2）由G为BC中点可得CG=CE，根据旋转的性质得∠D′CE′=∠DCE=90°，CE=CE′CE，则∠GCD′=∠DCE′=90°+α，然后根据“SAS”可判断△GCD′≌△E′CD，则GD′=E′D；（3）根据正方形的性质得CB=CD，而CD=CD′，则△BCD′与△DCD′为腰相等的两等腰三角形，当两顶角相等时它们全等，当△BCD′与△DCD′为钝角三角形时，可计算出α=135°，当△BCD′与△DCD′为锐角三角形时，可计算得到α=315°．解答：（1）解：∵长方形CEFD绕点C顺时针旋转至CE′F′D′，∴CD′=CD=2，在Rt△CED′中，CD′=2，CE=1，∴∠CD′E=30°，∵CD∥EF，∴∠α=30°；（2）证明：∵G为BC中点，∴CG=1，∴CG=CE，∵长方形CEFD绕点C顺时针旋转至CE′F′D′，∴∠D′CE′=∠DCE=90°，CE=CE′=CG，∴∠GCD′=∠DCE′=90°+α，.\n.在△GCD′和△E′CD中，∴△GCD′≌△E′CD（SAS），∴GD′=E′D；（3）解：能．理由如下：∵四边形ABCD为正方形，∴CB=CD，∵CD′=CD′，∴△BCD′与△DCD′为腰相等的两等腰三角形，当∠BCD′=∠DCD′时，△BCD′≌△DCD′，当△BCD′与△DCD′为钝角三角形时，则旋转角α==135°，当△BCD′与△DCD′为锐角三角形时，∠BCD′=∠DCD′=∠BCD=45°则α=360°﹣=315°，即旋转角a的值为135°或315°时，△BCD′与△DCD′全等．点评：.\n.本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了正方形、矩形的性质以及三角形全等的判定与性质．　20．（2013•）如图1，在△ABC中，∠A=36°，AB=AC，∠ABC的平分线BE交AC于E．（1）求证：AE=BC；（2）如图（2），过点E作EF∥BC交AB于F，将△AEF绕点A逆时针旋转角α（0°＜α＜144°）得到△AE′F′，连结CE′，BF′，求证：CE′=BF′；（3）在（2）的旋转过程中是否存在CE′∥AB？若存在，求出相应的旋转角α；若不存在，请说明理由．考点：旋转的性质；等腰三角形的性质；等腰梯形的判定．菁优网所有专题：压轴题．分析：（1）根据等腰三角形的性质以及角平分线的性质得出对应角之间的关系进而得出答案；.\n.（2）由旋转的性质可知：∠E′AC=∠F′AB，AE′=AF′，根据全等三角形证明方法得出即可；（3）分别根据①当点E的像E′与点M重合时，则四边形ABCM为等腰梯形，②当点E的像E′与点N重合时，求出α即可．解答：（1）证明：∵AB=BC，∠A=36°，∴∠ABC=∠C=72°，又∵BE平分∠ABC，∴∠ABE=∠CBE=36°，∴∠BEC=180°﹣∠C﹣∠CBE=72°，∴∠ABE=∠A，∠BEC=∠C，∴AE=BE，BE=BC，∴AE=BC．（2）证明：∵AC=AB且EF∥BC，∴AE=AF；由旋转的性质可知：∠E′AC=∠F′AB，AE′=AF′，∵在△CAE′和△BAF′中，∴△CAE′≌△BAF′，∴CE′=BF′．.\n.（3）存在CE′∥AB，理由：由（1）可知AE=BC，所以，在△AEF绕点A逆时针旋转过程中，E点经过的路径（圆弧）与过点C且与AB平行的直线l交于M、N两点，如图：①当点E的像E′与点M重合时，则四边形ABCM为等腰梯形，∴∠BAM=∠ABC=72°，又∠BAC=36°，∴α=∠CAM=36°．②当点E的像E′与点N重合时，由AB∥l得，∠AMN=∠BAM=72°，∵AM=AN，∴∠ANM=∠AMN=72°，∴∠MAN=180°﹣2×72°=36°，∴α=∠CAN=∠CAM+∠MAN=72°．所以，当旋转角为36°或72°时，CE′∥AB．点评：.\n.此题主要考查了旋转的性质以及等腰三角形的性质和等腰梯形的性质等知识，根据数形结合熟练掌握相关定理是解题关键．　21．（2013•崇左）如图所示，正方形ABCD中，E是CD上一点，F在CB的延长线上，且DE=BF．（1）求证：△ADE≌△ABF；（2）问：将△ADE顺时针旋转多少度后与△ABF重合，旋转中心是什么？考点：旋转的性质；直角三角形全等的判定；正方形的性质．菁优网所有专题：证明题；操作型．分析：（1）根据SAS定理，即可证明两三角形相似；（2）将△ADE顺时针旋转后与△ABF重合，A不变，因而旋转中心是A，∠DAB是旋转角，是90度．解答：（1）证明：在正方形ABCD中，∠D=∠ABC=90°，∴∠ABF=90°，∴∠D=∠ABF=90°，又DE=BF，AD=AB，∴△ADE≌△ABF．.\n.（2）解：将△ADE顺时针旋转90后与△ABF重合，旋转中心是点A．点评：本题主要考查了三角形全等的判定方法，以及旋转的定义，正确理解旋转的定义是解决本题的关键．　22．（2014春•江都市校级月考）作图题：（1）作出四边形ABCD关于O点成中心对称的四边形A′B′C′D′（如图1）；（2）在如图的方格纸中，每个小方格都是边长为1个单位的正方形，△ABC的三个顶点都在格点上（每个小方格的顶点叫格点）．画出△ABC绕点O顺时针旋转90°后的△A1B1C1．（如图2）考点：作图-旋转变换．菁优网所有专题：作图题．分析：（1）连接AO并延长至A′，使A′O=AO，连接BO并延长至B′，使B′O=BO，连接CO并延长至C′，使C′O=CO，连接DO并延长至D′，使D′O=DO，然后顺次连接即可；.\n.（2）根据网格结构找出点A、B、C绕点O顺时针旋转90°的对应点A1、B1、C1的位置，然后顺次连接即可．解答：解：（1）四边形A′B′C′D′如图所示；（2）△A1B1C1如图所示．点评：本题考查了利用旋转变换作图，熟记旋转的性质并准确找出对应点的位置是解题的关键．　23．（2014春•邵东县校级月考）如图，已知△ABC的三个顶点的坐标分别为A（﹣1，2）、B（﹣3，0）、C（0，0）．（1）请画出△ABC绕点A顺时针旋转90°的图形△AB1C1；（2）以C为位似中心，在x轴下方作△ABC的位似图形△A2B2C2，使△ABC放大，位似比为2：1，请画出图形，并求出△A2B2C的面积；（3）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标．.\n.考点：作图-旋转变换；平行四边形的判定；作图-位似变换．菁优网所有专题：网格型；分类讨论．分析：（1）把点C和点B分别绕点A顺时针旋转90°得到C1和B1，顺次连接即可；（2）连接AC延长到A2使A2C=2AC，延长BC到B2，使B2C=2BC，点C2的对应点为C，顺次连接各点即可，△A2B2C的面积=×底边×高．（3）根据平行四边形的对边平行且相等，分AB、BC、AC是对角线三种情况分别写出即可．解答：解：（1）如图所示，△AB1C1即为所作：.\n.（2）如图所示△A2B2C即为所作，由图中可知B2C为6，A2纵坐标为﹣4，所以B2C2上的高为4，故S=×6×4=12；（3）当AC为对角线时，点D坐标为（2，2）；当AB为对角线时，点D坐标为（﹣4，2）；当BC为对角线时，点D坐标为（﹣2，﹣2）．点评：.\n.本题主要考查了作图﹣旋转变换、作图﹣位似变换以及平行四边形的判定的知识，解答本题的关键是画位似图形的一般步骤：①确定位似中心，②分别连接并延长位似中心和能代表原图的关键点；③根据相似比，确定能代表所作的位似图形的关键点；顺次连接上述各点．　24．（2014秋•泰兴市校级月考）已知，如图▱ABCD中，AB⊥AC，AB=1，BC=，对角线AC、BD交于0点，将直线AC绕点0顺时针旋转，分别交BC、AD于点E、F（1）求证：AF=EC；（2）在旋转过程中，四边形BEDF可能是菱形吗？如果不能，请说明理由；如果能，说明理由并求出此时AC绕点0顺时针旋转的度数．考点：旋转的性质；平行四边形的性质；菱形的判定．菁优网所有分析：（1）证明△AOF≌△COE，根据全等三角形的性质证明结论；（2）根据对角线互相垂直的平行四边形是菱形，求出AC绕点0顺时针旋转的度数．解答：（1）证明：∵四边形ABCD是平行四边形，∴OA=OC，AD∥BC，∴∠OAF=∠OCE，在△AOF和△COE中，，.\n.∴△AOF≌△COE，∴AF=EC；（2）∵△AOF≌△COE，∴OE=OF，又OB=OD，∴四边形BEDF是平行四边形，当EF⊥BD时，四边形BEDF是菱形，∵AB⊥AC，AB=1，BC=，由勾股定理，AC=2，则OA=1，又AB=1，∠OAB=90°，∴∠AOB=45°，∴AC绕点0顺时针旋转45°时，四边形BEDF是菱形．点评：本题考查的是菱形的判定，正确运用三角形全等的判定定理、平行四边形的判定和性质定理以及旋转的知识的解题的关键，注意：对角线互相垂直的平行四边形是菱形．　25．（2014秋•校级月考）已知：如图，点E是正方形ABCD的边AB上一点，点F是边BC上一点，且AE+CF=EF．求∠EDF的度数．.\n.考点：旋转的性质；全等三角形的判定与性质；正方形的性质．菁优网所有专题：计算题．分析：先根据正方形的性质得DA=DC，∠ADC=90°，于是可把△DAE绕点D逆时针旋转90°得△DCG，如图，根据旋转的性质得CG=AE，DE=DG，∠DCG=∠A=90°，∠EDG=90°，则可判断点G在BC的延长线上和EF=GF，接着证明△DEF≌△DGF，根据全等三角形的性质得∠EDF=∠GDF，所以∠EDF=∠EDG=45°．解答：解：∵四边形ABCD为正方形，∴DA=DC，∠ADC=90°∴把△DAE绕点D逆时针旋转90°可得△DCG，如图，∴CG=AE，DE=DG，∠DCG=∠A=90°，∠EDG=90°，∴点G在BC的延长线上，而AE+CF=EF，∴CG+CF=EF，即EF=GF，.\n.在△DEF和△DGF中，∴△DEF≌△DGF，∴∠EDF=∠GDF，∴∠EDF=∠EDG=45°．点评：本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了全等三角形的判定与性质和正方形的性质．　26．（2014春•永定县校级月考）如图，点E是正方形ABCD一点，连接AE、BE、CE，将△ABE绕点B顺时针旋转90°到△CBE的位置．若AE=1，BE=2，CE=3，则求∠BE′C的度数．（提示：连接EE′）考点：.\n.旋转的性质；勾股定理的逆定理；等腰直角三角形；正方形的性质．菁优网所有专题：计算题．分析：连接EE′，如图，根据旋转的性质得BE=BE′=2，AE=CE′=1，∠EBE′=90°，则可判断△BEE′为等腰直角三角形，根据等腰直角三角形的性质得EE′=BE=2，∠BE′E=45°，在△CEE′中，由于CE′2+EE′2=CE2，根据勾股定理的逆定理得到△CEE′为直角三角形，即∠EE′C=90°，然后利用∠BE′C=∠BE′E+∠CE′E求解．解答：解：连接EE′，如图，∵△ABE绕点B顺时针旋转90°得到△CBE′，∴BE=BE′=2，AE=CE′=1，∠EBE′=90°，∴△BEE′为等腰直角三角形，∴EE′=BE=2，∠BE′E=45°，在△CEE′中，CE=3，CE′=1，EE′=2，∵12+（2）2=32，∴CE′2+EE′2=CE2，.\n.∴△CEE′为直角三角形，∴∠EE′C=90°，∴∠BE′C=∠BE′E+∠CE′E=135°．点评：本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了勾股定理的逆定理、等腰直角三角形的判定与性质和正方形的性质．　27．（2014春•涟水县校级月考）如图，在Rt△ABC中，∠ACB=90°，∠A=20°，将△ABC绕点C按顺时针方向旋转后得到△EDC，此时点D在AB边上，求旋转角的大小．考点：旋转的性质．菁优网所有分析：.\n.根据直角三角形两锐角互余求出∠B，再根据旋转的性质可得BC=CD，然后利用等腰三角形两底角相等列式求出∠BCD，再根据旋转角等于对应边BC、CD的夹角解答．解答：解：∵∠ACB=90°，∠A=20°，∴∠B=90°﹣∠A=90°﹣20°=70°，∵△ABC绕点C按顺时针方向旋转后得到△EDC，∴BC=CD，∴∠B=∠BDC，在△BCD中，∠BCD=180°﹣2∠B=180°﹣2×70°=40°，∴旋转角是40°．点评：本题考查了旋转的性质，直角三角形两锐角互余的性质，等腰三角形的性质，熟记各性质并求出BC=CD是解题的关键．　28．（2014秋•明山区校级月考）如图，已知△BAD≌△BCE，∠BAD=∠BCE=90°，∠ABD=∠BEC=30°，点M为DE的中点，过点E与AD平行的直线交射线AM于点N．（1）如图1，当A，B，E三点在同一直线上时，判断AC与CN数量关系为　AC=CN　；（2）将图1中△BCE绕点B逆时针旋转到图2位置时，（1）中的结论是否仍成立？若成立，试证明之，若不成立，请说明理由；（3）将图1中△BCE绕点B逆时针旋转一周，旋转过程中△CAN能否为等腰直角三角形？若能，直接写出旋转角度；若不能，说明理由．.\n.考点：旋转的性质；全等三角形的判定与性质．菁优网所有分析：（1）首先证明△MEN≌△MDA，得BC=EN；然后证明△ABC≌△CEN，得到AC=CN；（2）与（1）同理可证明结论仍然成立；（3）当旋转角为60°时，△CAN能成为等腰直角三角形，此时点A、B、C在一条直线上，点N、E、C在一条直线上．解答：解：（1）AC与CN数量关系为：AC=CN．理由如下：∵△BAD≌△BCE，∴BC=AD，EC=AB．∵EN∥AD，∴∠MEN=∠MDA．在△MEN与△MDA中，，.\n.∴△MEN≌△MDA（ASA），∴EN=AD，∴EN=BC．在△ABC与△CEN中，，∴△ABC≌△CEN（SAS），∴AC=CN．（2）结论仍然成立．理由如下：与（1）同理，可证明△MEN≌△MDA，∴EN=BC．设旋转角为α，则∠ABC=120°+α，∠DBE=360°﹣∠DBA﹣∠ABC﹣∠CBE=360°﹣30°﹣（120°+α）﹣60°=150°﹣α．∵BD=BE，∴∠BED=∠BDE=（180°﹣∠DBE）=15°+α．∵EN∥AD，∴∠MEN=∠MDA=∠ADB+∠BDE=60°+（15°+α）=75°+α．.\n.∴∠CEN=∠CEB+∠BED+∠MEN=30°+（15°+α）+（75°+α）=120°+α，∴∠ABC=∠CEN．在△ABC与△CEN中，，∴△ABC≌△CEN（SAS），∴AC=CN．（3）△CAN能成为等腰直角三角形，此时旋转角为60°．如下图所示：此时旋转角为60°或240°，点A、B、C在一条直线上，点N、E、C在一条直线上．点评：本题考查了图形的旋转变换．解题要点是由旋转性质得出旋转过程中不变的量，再利用全等三角形证明题设中的结论．.\n.　29．（2014秋•闽侯县校级月考）如图，在平面直角坐标系中，已知△AOB是等边三角形，点A的坐标是（0，3），点B在第一象限，∠OAB的平分线交x轴于点P，把△AOP绕着点A按逆时针方向旋转，使边AO与AB重合，得到△ABD，连接DP．求：DP的长及点D的坐标．考点：坐标与图形变化-旋转．菁优网所有分析：根据等边三角形的每一个角都是60°可得∠OAB=60°，然后根据对应边的夹角∠OAB为旋转角求出∠PAD=60°，再判断出△APD是等边三角形，根据等边三角形的三条边都相等可得DP=AP，根据，∠OAB的平分线交x轴于点P，∠OAP=30°，利用三角函数求出AP，从而得到DP，再求出∠OAD=90°，然后写出点D的坐标即可．解答：解：∵△AOB是等边三角形，∴∠OAB=60°，∵△AOP绕着点A按逆时针方向旋转边AO与AB重合，.\n.∴旋转角=∠OAB=∠PAD=60°，AD=AP，∴△APD是等边三角形，∴DP=AP，∠PAD=60°，∵A的坐标是（0，3），∠OAB的平分线交x轴于点P，∴∠OAP=30°，AP==2，∴DP=AP=2，∵∠OAP=30°，∠PAD=60°，∴∠OAD=30°+60°=90°，∴点D的坐标为（2，3）．点评：本题考查了旋转的性质，坐标与图形性质，等边三角形的判定与性质，解直角三角形，熟记各性质并判断出△APD是等边三角形是解题的关键．　30．（2014春•泰兴市校级月考）如图①，两个全等的等腰直角△ABC和△EDC中，∠ACB=∠ECD=90°，点A与点E重合，点D与点B重合．现△ABC不动，把△EDC绕点C按顺时针方向旋转，旋转角为α（0°＜α＜90°）．（1）如图②，AB与CE交于F，ED与AB、BC分别交于M、H．求证：CF=CH；.\n.（2）如图③，当α=45°时，试判断四边形ACDM是什么四边形，并说明理由；（3）如图②，在△EDC绕点C旋转的过程中，连接BD，当旋转角α的度数为　30°　时，△BDH是等腰三角形．考点：旋转的性质；全等三角形的判定与性质；菱形的判定．菁优网所有专题：证明题．分析：（1）根据两个全等的等腰直角△ABC和△EDC得到∠A=∠B=∠E=∠D=45°，CA=CB=CE=CD，再根据旋转的性质得CA=CD，∠A=∠D，∠ACE=∠BCD=α，可证明△CAF≌△CDH，所以CF=CH；（2）由于∠ACE=∠BCD=45°，∠A=45°，根据三角形角和定理得∠AFC=90°，而∠FCD=90°，根据平行线的判定可得到AB∥CD，同理可得AC∥DE，则可判断四边形ACDM是平行四边形，加上CA=CD，于是可判断四边形ACDM是菱形；（3）根据旋转的性质得到CB=CD，∠BCD=α，根据等腰三角形的性质和三角形角和定理得∠CBD=∠CDB=（180°﹣α），则∠HBD＞∠BDH，则当DB=DH或BH=BD时，△BDH是等腰三角形，根据三角形外角性质得∠BHD=∠HCD+∠HDC=α+45°，当DB=DH，则∠HBD=∠BHD，即（180°﹣α）=α+45°，解得α=30°；当BH=BD，则∠BHD=∠BDH，即α+45°=（180°﹣α）﹣45°，解得α=0（舍去），所以α=30°．解答：（1）证明：∵△ABC和△EDC是全等的等腰直角三角形，∴∠A=∠B=∠E=∠D=45°，CA=CB=CE=CD，∵△ABC不动，把△EDC绕点C按顺时针方向旋转，旋转角为α，∴CA=CD，∠A=∠D，∠ACE=∠BCD=α，在△CAF和△CDH中，∴△CAF≌△CDH，∴CF=CH；（2）解：四边形ACDM是菱形．理由如下：∵∠ACE=∠BCD=45°，而∠A=45°，∴∠AFC=90°，而∠FCD=90°，∴AB∥CD，同理可得AC∥DE，∴四边形ACDM是平行四边形，而CA=CD，∴四边形ACDM是菱形；（3）解：∵CB=CD，∠BCD=α，∴∠CBD=∠CDB=（180°﹣α），.\n.∴∠HBD＞∠BDH，∴当DB=DH或BH=BD时，△BDH是等腰三角形，∵∠BHD=∠HCD+∠HDC=α+45°，当DB=DH，则∠HBD=∠BHD，即（180°﹣α）=α+45°，解得α=30°；当BH=BD，则∠BHD=∠BDH，即α+45°=（180°﹣α）﹣45°，解得α=0（舍去），∴α=30°，即当旋转角α的度数为30°时，△BDH是等腰三角形．故答案为30°．点评：本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了全等三角形的判定与性质、菱形的判定和等腰三角形的性质．　.