- 1.78 MB
- 2022-09-06 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
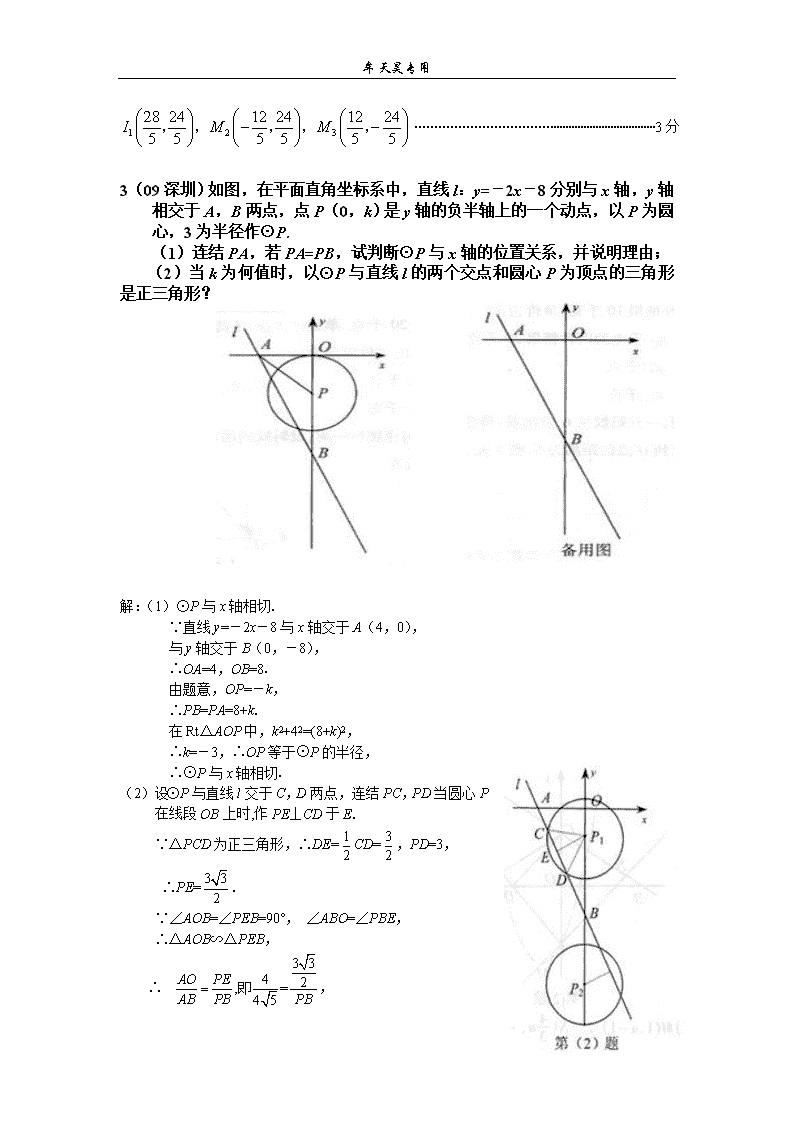
牟天昊专用动点问题专题训练1、(09包头)如图,已知中,厘米,厘米,点为的中点.(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.AQCDBP①若点Q的运动速度与点P的运动速度相等,经过1秒后,与是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使与全等?(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿三边运动,求经过多长时间点P与点Q第一次在的哪条边上相遇?解:(1)①∵秒,∴厘米,∵厘米,点为的中点,∴厘米.又∵厘米,∴厘米,∴.又∵,∴,∴.(4分)②∵,∴,又∵,,则,∴点,点运动的时间秒,∴厘米/秒.(7分)(2)设经过秒后点与点第一次相遇,由题意,得,解得秒.23/23\n牟天昊专用∴点共运动了厘米.∵,∴点、点在边上相遇,∴经过秒点与点第一次在边上相遇.(12分)2、(09齐齐哈尔)直线与坐标轴分别交于两点,动点同时从点出发,同时到达点,运动停止.点沿线段运动,速度为每秒1个单位长度,点沿路线→→运动.(1)直接写出两点的坐标;(2)设点的运动时间为秒,的面积为,求出与之间的函数关系式;xAOQPBy(3)当时,求出点的坐标,并直接写出以点为顶点的平行四边形的第四个顶点的坐标.解(1)A(8,0)B(0,6)1分(2)点由到的时间是(秒)点的速度是(单位/秒)1分当在线段上运动(或0)时,1分当在线段上运动(或)时,,如图,作于点,由,得,1分1分(自变量取值范围写对给1分,否则不给分.)(3)1分23/23\n牟天昊专用3分3(09深圳)如图,在平面直角坐标系中,直线l:y=-2x-8分别与x轴,y轴相交于A,B两点,点P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.(1)连结PA,若PA=PB,试判断⊙P与x轴的位置关系,并说明理由;(2)当k为何值时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形?解:(1)⊙P与x轴相切.∵直线y=-2x-8与x轴交于A(4,0),与y轴交于B(0,-8),∴OA=4,OB=8.由题意,OP=-k,∴PB=PA=8+k.在Rt△AOP中,k2+42=(8+k)2,∴k=-3,∴OP等于⊙P的半径,∴⊙P与x轴相切.(2)设⊙P与直线l交于C,D两点,连结PC,PD当圆心P在线段OB上时,作PE⊥CD于E.∵△PCD为正三角形,∴DE=CD=,PD=3,∴PE=.∵∠AOB=∠PEB=90°,∠ABO=∠PBE,∴△AOB∽△PEB,∴,23/23\n牟天昊专用∴∴,∴,∴.当圆心P在线段OB延长线上时,同理可得P(0,--8),∴k=--8,∴当k=-8或k=--8时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形.4(09哈尔滨)如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H.(1)求直线AC的解析式;(2)连接BM,如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);(3)在(2)的条件下,当t为何值时,∠MPB与∠BCO互为余角,并求此时直线OP与直线AC所夹锐角的正切值.23/23\n牟天昊专用解:23/23\n牟天昊专用ACBPQED图165(09河北)在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).(1)当t=2时,AP=,点Q到AC的距离是;ACBPQED图4(2)在点P从C向A运动的过程中,求△APQ的面积S与t的函数关系式;(不必写出t的取值范围)(3)在点E从B向C运动的过程中,四边形QBED能否成为直角梯形?若能,求t的值.若不能,请说明理由;(4)当DE经过点C 时,请直接写出t的值.ACBPQED图5AC(E))BPQD图6GAC(E))BPQD图7G解:(1)1,;(2)作QF⊥AC于点F,如图3,AQ=CP=t,∴.由△AQF∽△ABC,,得.∴.∴,即.(3)能.①当DE∥QB时,如图4.∵DE⊥PQ,∴PQ⊥QB,四边形QBED是直角梯形.此时∠AQP=90°.由△APQ ∽△ABC,得,即.解得.②如图5,当PQ∥BC时,DE⊥BC,四边形QBED是直角梯形.此时∠APQ=90°.由△AQP ∽△ABC,得,即.解得.23/23\n牟天昊专用(4)或.①点P由C向A运动,DE经过点C.连接QC,作QG⊥BC于点G,如图6.,.由,得,解得.②点P由A向C运动,DE经过点C,如图7.,】6(09河南))如图,在中,,.点是的中点,过点的直线从与重合的位置开始,绕点作逆时针旋转,交OECBDAlOCBA(备用图)边于点.过点作交直线于点,设直线的旋转角为.(1)①当度时,四边形是等腰梯形,此时的长为;②当度时,四边形是直角梯形,此时的长为;(2)当时,判断四边形是否为菱形,并说明理由.解(1)①30,1;②60,1.5;……………………4分(2)当∠α=900时,四边形EDBC是菱形.∵∠α=∠ACB=900,∴BC//ED.∵CE//AB,∴四边形EDBC是平行四边形.……………………6分在Rt△ABC中,∠ACB=900,∠B=600,BC=2,∴∠A=300.∴AB=4,AC=2.∴AO==.……………………8分在Rt△AOD中,∠A=300,∴AD=2.∴BD=2.23/23\n牟天昊专用∴BD=BC.又∵四边形EDBC是平行四边形,∴四边形EDBC是菱形……………………10分ADCBMN7(09济南)如图,在梯形中,动点从点出发沿线段以每秒2个单位长度的速度向终点运动;动点同时从点出发沿线段以每秒1个单位长度的速度向终点运动.设运动的时间为秒.(1)求的长.(2)当时,求的值.(3)试探究:为何值时,为等腰三角形.解:(1)如图①,过、分别作于,于,则四边形是矩形∴1分在中,2分在中,由勾股定理得,∴3分(图①)ADCBKH(图②)ADCBGMN(2)如图②,过作交于点,则四边形是平行四边形∵∴∴∴4分由题意知,当、运动到秒时,∵∴又∴23/23\n牟天昊专用∴5分即解得,6分(3)分三种情况讨论:①当时,如图③,即∴7分ADCBMN(图③)(图④)ADCBMNHE②当时,如图④,过作于解法一:由等腰三角形三线合一性质得在中,又在中,∴解得8分解法二:∵∴∴即∴8分③当时,如图⑤,过作于点.解法一:(方法同②中解法一)23/23\n牟天昊专用(图⑤)ADCBHNMF解得解法二:∵∴∴即∴综上所述,当、或时,为等腰三角形9分8(09江西)如图1,在等腰梯形中,,是的中点,过点作交于点.,.(1)求点到的距离;(2)点为线段上的一个动点,过作交于点,过作交折线于点,连结,设.①当点在线段上时(如图2),的形状是否发生改变?若不变,求出的周长;若改变,请说明理由;②当点在线段上时(如图3),是否存在点,使为等腰三角形?若存在,请求出所有满足要求的的值;若不存在,请说明理由.ADEBFC图4(备用)ADEBFC图5(备用)ADEBFC图1图2ADEBFCPNM图3ADEBFCPNM(第25题)23/23\n牟天昊专用解(1)如图1,过点作于点1分图1ADEBFCG∵为的中点,∴在中,∴2分∴即点到的距离为3分(2)①当点在线段上运动时,的形状不发生改变.∵∴∵∴,同理4分如图2,过点作于,∵图2ADEBFCPNMGH∴∴∴则在中,∴的周长=6分②当点在线段上运动时,的形状发生改变,但恒为等边三角形.当时,如图3,作于,则类似①,∴7分∵是等边三角形,∴此时,8分图3ADEBFCPNM图4ADEBFCPMN图5ADEBF(P)CMNGGRG23/23\n牟天昊专用当时,如图4,这时此时,当时,如图5,则又∴因此点与重合,为直角三角形.∴此时,综上所述,当或4或时,为等腰三角形.10分9(09兰州)如图①,正方形ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以相同速度在x轴正半轴上运动,当P点到达D点时,两点同时停止运动,设运动的时间为t秒.(1)当P点在边AB上运动时,点Q的横坐标(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;(2)求正方形边长及顶点C的坐标;(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标;(4)如果点P、Q保持原速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等,若能,写出所有符合条件的t的值;若不能,请说明理由.解:(1)(1,0)1分点P运动速度每秒钟1个单位长度.2分(2)过点作BF⊥y轴于点,⊥轴于点,则=8,.∴.在Rt△AFB中,3分过点作⊥轴于点,与的延长线交于点.23/23\n牟天昊专用∵∴△ABF≌△BCH.∴.∴.∴所求C点的坐标为(14,12).4分(3)过点P作PM⊥y轴于点M,PN⊥轴于点N,则△APM∽△ABF.∴..∴.∴.设△OPQ的面积为(平方单位)∴(0≤≤10)5分说明:未注明自变量的取值范围不扣分.∵<0∴当时,△OPQ的面积最大.6分此时P的坐标为(,).7分(4)当或时,OP与PQ相等.9分10(09临沂)数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.,且EF交正方形外角的平行线CF于点F,求证:AE=EF.经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证,所以.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.ADFCGEB图1ADFCGEB图2ADFCGEB图323/23\n牟天昊专用23/23\n牟天昊专用解:(1)正确.(1分)ADFCGEBM证明:在上取一点,使,连接.(2分).,.是外角平分线,,..,,.(ASA).(5分).(6分)(2)正确.(7分)证明:在的延长线上取一点.ADFCGEBN使,连接.(8分)..四边形是正方形,...(ASA).(10分).(11分)11(09天津)已知一个直角三角形纸片,其中.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边交于点,与边交于点.xyBOA(Ⅰ)若折叠后使点与点重合,求点的坐标;xyBOA(Ⅱ)若折叠后点落在边上的点为,设,,试写出关于的函数解析式,并确定的取值范围;(Ⅲ)若折叠后点落在边上的点为,且使,求此时点的坐标.xyBOA23/23\n牟天昊专用解(Ⅰ)如图①,折叠后点与点重合,则.设点的坐标为.则.于是.在中,由勾股定理,得,即,解得.点的坐标为.4分(Ⅱ)如图②,折叠后点落在边上的点为,则.由题设,则,在中,由勾股定理,得.,即6分由点在边上,有,解析式为所求.当时,随的增大而减小,的取值范围为.7分(Ⅲ)如图③,折叠后点落在边上的点为,且.则.又,有..有,得.9分在中,设,则.由(Ⅱ)的结论,得,23/23\n牟天昊专用解得.点的坐标为.10分12图(1)ABCDEFMN(09太原)问题解决如图(1),将正方形纸片折叠,使点落在边上一点(不与点,重合),压平后得到折痕.当时,求的值.方法指导:为了求得的值,可先求、的长,不妨设:=2类比归纳在图(1)中,若则的值等于;若则的值等于;若(为整数),则的值等于.(用含的式子表示)联系拓广图(2)NABCDEFM如图(2),将矩形纸片折叠,使点落在边上一点(不与点重合),压平后得到折痕设则的值等于.(用含的式子表示)解:方法一:如图(1-1),连接.N图(1-1)ABCDEFM23/23\n牟天昊专用由题设,得四边形和四边形关于直线对称.∴垂直平分.∴1分∵四边形是正方形,∴∵设则在中,.∴解得,即3分在和在中,,,5分设则∴解得即6分∴7分方法二:同方法一,3分如图(1-2),过点做交于点,连接N图(1-2)ABCDEFMG ∵∴四边形是平行四边形.∴同理,四边形也是平行四边形.∴ ∵ 在与中 ∴5分23/23\n牟天昊专用∵6分∴7分类比归纳(或);;10分联系拓广12分1.(2008,河北)如图所示,直线L1的解析表达式为y=-3x+3,且L1与x轴交于点D.直线L2经过点A,B,直线L1,L2交于点C.(1)求点D的坐标;(2)求直线L2的解析表达式;(3)求△ADC的面积;(4)在直线L2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.2.(2005,长春市)如图a所示,矩形ABCD的两条边在坐标轴上,点D与原点重合,对角线BD所在直线的函数关系式为y=x,AD=8.矩形ABCD沿DB方向以每秒1单位长度运动,同时点P从点A出发做匀速运动,沿矩形ABCD的边经过点B到达点C,用了14s.(1)23/23\n牟天昊专用求矩形ABCD的周长.(2)如图b所示,图形运动到第5s时,求点P的坐标;(3)设矩形运动的时间为t.当0≤t≤6时,点P所经过的路线是一条线段,请求出线段所在直线的函数关系式;(4)当点P在线段AB或BC上运动时,过点P作x轴,y轴的垂线,垂足分别为E,F,则矩形PEOF是否能与矩形ABCD相似(或位似)?若能,求出t的值;若不能,说明理由.3.(08金华)如图1,在平面直角坐标系中,己知ΔAOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连结AP,并把ΔAOP绕着点A按逆时针方向旋转.使边AO与AB重合.得到ΔABD。(1)求直线AB的解析式;(2)当点P运动到点(,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使ΔOPD的面积等于,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由。4.已知直线y=kx+b与x轴交于M,与y轴交于N(N点在M点上方),在直线上存在一点P(m,n)(m>0),连结OP,作PA垂直于OP交x轴于A(a,0)(a>0)(1)kb0(填“>”、”<”或“=”);(1分)(2)若y=1-x且n为20以内整数,y1=2/x1,y2=x23/2,当x1=x2=n时,(y1+y2)n/2的最小值;(5分)23/23\n牟天昊专用5.如图,直线与x轴y轴分别交于点E、F,点E的坐标为(-8,0),点A的坐标为(-6,0)。(1)求的值;(2)若点P(,)是第二象限内的直线上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;(3)探究:当点P运动到什么位置时,△OPA的面积为,并说明理由。1.(1)由y=-3x+3知,令y=0,得-3x+3=0,∴x=1.∴D(1,0).(2)设直线L2的解析式表达式为y=kx+b,由图像知:直线L2过点A(4,0)和点B(3,-),∴,∴∴直线L的解析表达式为y=x-6.(3)由解得∴C(2,-3).∵AD=3,∴S△=×3×│-3│=.(4)P(6,3).2.(1)AD=8,B点在y=x上,则y=6,B点坐标为(8,6),AB=6,矩形的周长为28.(2)由(1)可知AB+BC=14,P点走过AB,BC的时间为14s,因此点P的速度为每秒1个单位.∵矩形沿DB方向以每秒1个单位长运动,出发5s后,OD=5,此时D点坐标为(4,3)同时,点P沿AB方向运动了5个单位,则点P坐标为(12,8).23/23\n牟天昊专用(3)点P运动前的位置为(8,0),5s后运动到(12,8)已知它运动路线是一条线段,设线段所在直线为y=kx+b.∴解得直线解析式为y=2x-16.(4)方法一:①当点P在AB边运动时,即0≤t≤6.点D的坐标为(t,t).∴点P的坐标为(8+t,t).若,则=,解得t=6.当t=6时,点P与点B重合,此时△PEO与△BAD相形.若,则=,解得t=20.因为20>6,所以此时点P不在AB边上,舍去.②当点P在BC边运动时,即6≤t≤14.点D的坐标为(t,t).∴点P的坐标为(14-t,t+6).若,则=,解得t=6.此情况①已讨论.若,则=,解得t=.因为>14,此时点P不在BC边上,舍去.综上,当t=6时,点P到达点B时,此时△PEO与△BAD相形.方法二:23/23\n牟天昊专用当点P在AB上没有到达点B时,=,更不能等于.则点P在AB上没到达点B时,两个三角形不能构成相似形.当点P到达点B时,△PEO与△BAD相似,此时t=6.当点P越过点B在BC上时,>.若=时,由点P在BC上时,坐标为(14-t,t+6),(6≤t≤14).=,解得t=,但>14.因此当P在BC上(不包括点B)时,△PEO与△BAD不相似.综上所述,当t=6时,点P到达点B,△PEO与△BAD是相似形.4.解:(1)kb<0(2)y=1-x,那么M(1,0),N(0,1) y1+y2=2/n+n3/2=(4+n4)/2n(y1+y2)n/2=(4+n4)/4=1+n4/4n4min=1(y1+y2)n/2min=5/423/23