初中四边形练习题 12页

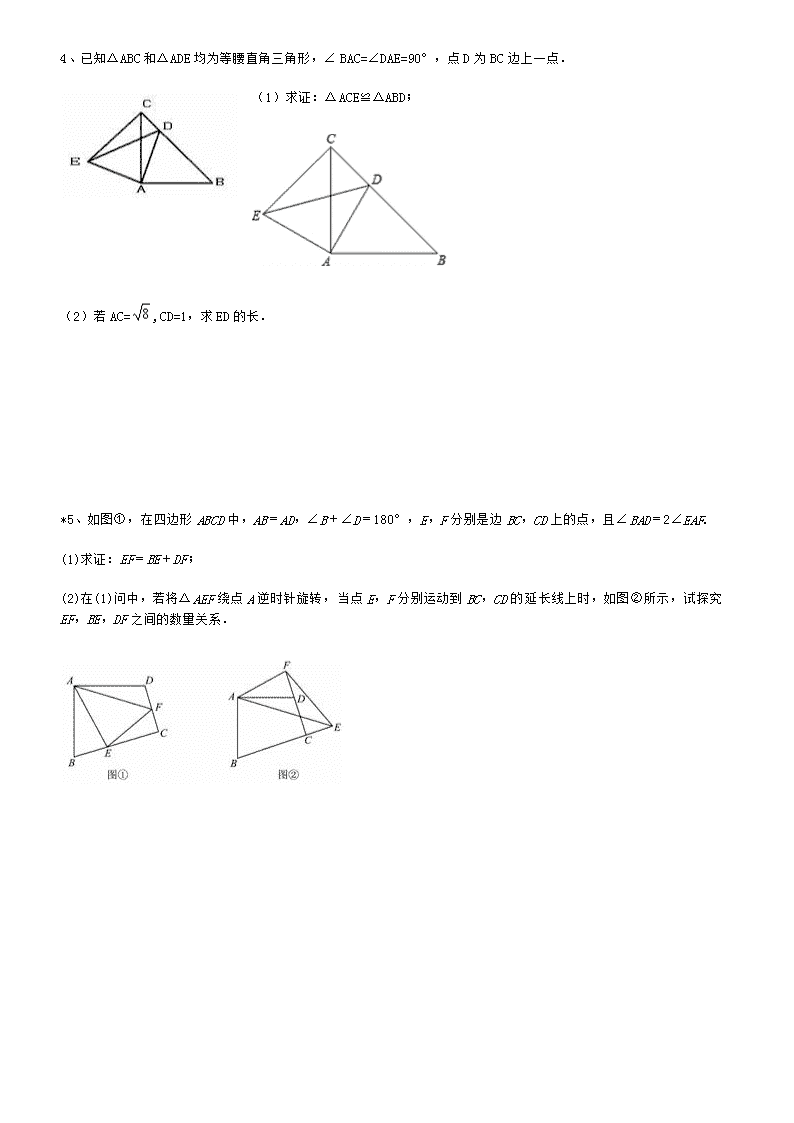
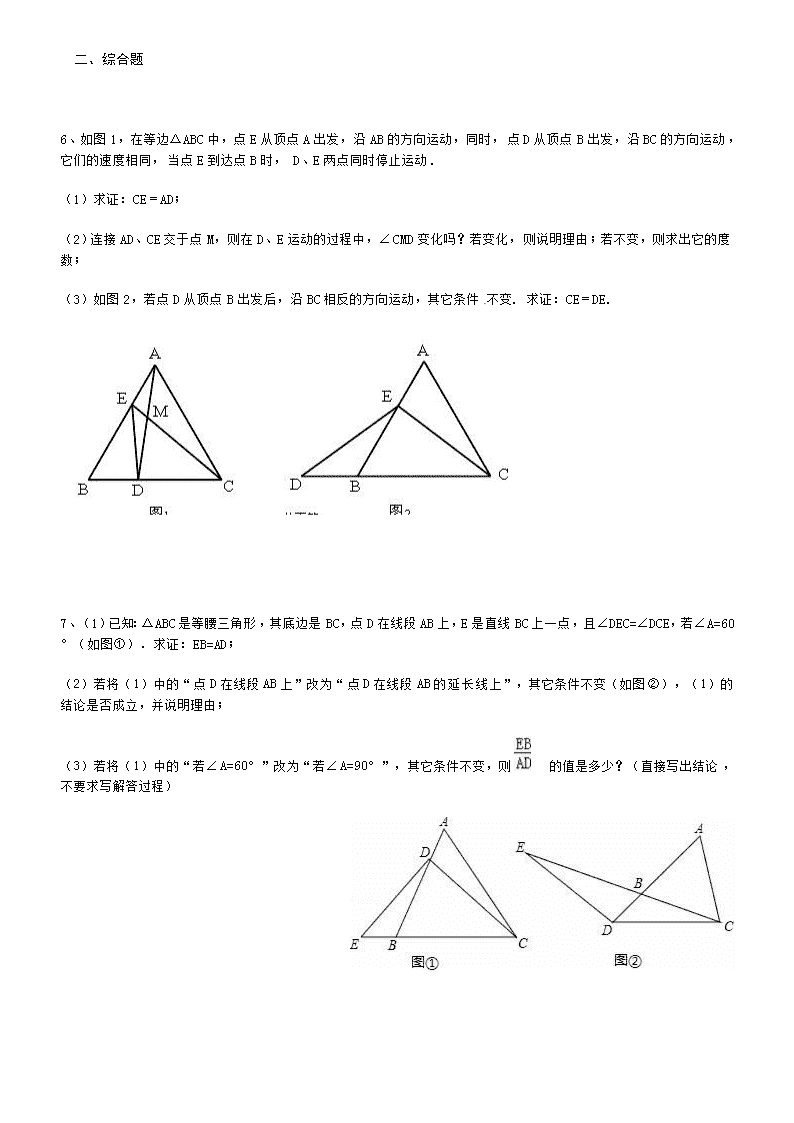
四边形练习题（作业）姓名：_______________班级：_______________考号：_______________一、简答题1、如图所示，在△ABC中，AB=20，AC=12，BC=16，把△ABC折迭， 使AB落在直线AC上，求重迭部分(阴影部分)的面积．2、如图，△ABC中，AD是高，CE是中线，点G是CE的中点，DG⊥CE，点G为垂足．说明（1）DC=BE； （2）若∠AEC=66°，求∠BCE的度数． 3、四边形OABC中，OA=a，OC=3，BC=2,∠AOC=∠BCO=90°，经过点O的直线l将四边形分成两部分，直线l与OC所成的角设为θ，将四边形OABC的直角∠OCB沿直线l折迭，点C落在点D处（如图1）．（1）若折迭后点D恰为AB的中点（如图2），则θ=       ；（2）若θ=45°，四边形OABC的直角∠OCB沿直线l折迭后，点B落在点四边形OABC的边AB上的E处（如图3），求a的值；\n4、已知△ABC和△ADE均为等腰直角三角形，∠BAC=∠DAE=90°，点D为BC边上一点．（1）求证：△ACE≌△ABD；（2）若AC=,CD=1，求ED的长．*5、如图①，在四边形ABCD中，AB＝AD，∠B＋∠D＝180°，E，F分别是边BC，CD上的点，且∠BAD＝2∠EAF.(1)求证：EF＝BE＋DF；(2)在(1)问中，若将△AEF绕点A逆时针旋转，当点E，F分别运动到BC，CD的延长线上时，如图②所示，试探究EF，BE，DF之间的数量关系．\n二、综合题6、如图1，在等边△ABC中，点E从顶点A出发，沿AB的方向运动，同时，点D从顶点B出发，沿BC的方向运动，它们的速度相同，当点E到达点B时，D、E两点同时停止运动.（1）求证：CE＝AD；（2）连接AD、CE交于点M，则在D、E运动的过程中，∠CMD变化吗？若变化，则说明理由；若不变，则求出它的度数；（3）如图2，若点D从顶点B出发后，沿BC相反的方向运动，其它条件不变.求证：CE＝DE.7、（1）已知：△ABC是等腰三角形，其底边是BC，点D在线段AB上，E是直线BC上一点，且∠DEC=∠DCE，若∠A=60°（如图①）．求证：EB=AD；                           （2）若将（1）中的“点D在线段AB上”改为“点D在线段AB的延长线上”，其它条件不变（如图②），（1）的结论是否成立，并说明理由；                                 （3）若将（1）中的“若∠A=60°”改为“若∠A=90°”，其它条件不变，则的值是多少？（直接写出结论，不要求写解答过程）                                                    \n*8、已知：如图，在矩形ABCD中，Ab=6cm，BC=8cm，对角线AC，BD交于点0．点P从点A出发，沿方向匀速运动，速度为1cm/s；同时，点Q从点D出发，沿DC方向匀速运动，速度为1cm/s；当一个点停止运动时，另一个点也停止运动．连接PO并延长，交BC于点E，过点Q作QF∥AC，交BD于点F．设运动时间为t（s）（0＜t＜6），解答下列问题：（1）当t为何值时，△AOP是等腰三角形？（2）设五边形OECQF的面积为S（cm2），试确定S与t的函数关系式；（3）在运动过程中，是否存在某一时刻t，使S五边形S五边形OECQF：S△ACD=9：16？若存在，求出t的值；若不存在，请说明理由；（4）在运动过程中，是否存在某一时刻t，使OD平分∠COP？若存在，求出t的值；若不存在，请说明理由．　\n参考答案一、简答题1、36(提示，先说明⊿ABC是直角三角形，再求出CD=6)2、（1）略（2）22°  3、（1）30°  （2）若点E四边形0ABC的边AB上，∴AB⊥直线l由折叠可知，OD=OC=3，DE=BC=2．∵θ=45°，AB⊥直线l，∴△ADE为等腰直角三角形，∴AD=DE=2，∴OA=OD+AD=3+2=5，∴a=5；4、（1）略（2）   5、解：(1)延长CB至点M，使BM＝DF，连结AM，∵∠ABM＋∠ABC＝180°，∠D＋∠ABC＝180°，∴∠ABM＝∠D，又AB＝AD，∴△ABM≌△ADF(SAS)，∴AM＝AF，∠BAM＝∠DAF，∴∠MAE＝∠BAM＋∠BAE＝∠DAF＋∠BAE＝∠BAD－∠EAF＝∠EAF，又AE＝AE，∴△EAM≌△EAF(SAS)，∴EF＝EM＝BE＋DF(2)EF＝BE－DF，证明：在BE上截取BN＝DF，连结AN，∵∠ADF＋∠ADC＝180°，∠B＋∠ADC＝180°，∴∠B＝∠ADF，又AB＝AD，∴△ABN≌△ADF(SAS)，∴AN＝AF，∠BAN＝∠DAF，∴∠NAE＝∠BAD－(∠BAN＋∠EAD)＝∠BAD－(∠DAF＋∠EAD)＝∠BAD－∠EAF＝2∠EAF－∠EAF＝∠EAF，又AE＝AE，∴△EAN≌△EAF(SAS)，∴EF＝EN＝BE－BN＝BE－DF二、综合题\n6、7、【分析】（1）作DF∥BC交AC于F，由平行线的性质得出∠ADF=∠ABC，∠AFD=∠ACB，∠FDC=∠DCE，证明△ABC是等边三角形，得出∠ABC=∠ACB=60°，证出△ADF是等边三角形，∠DFC=120°，得出AD=DF，由已知条件得出∠FDC=∠DEC，ED=CD，由AAS证明△DBE≌△CFD，得出EB=DF，即可得出结论；                  （2）作DF∥BC交AC的延长线于F，同（1）证出△DBE≌△CFD，得出EB=DF，即可得出结论；        （3）作DF∥BC交AC于F，同（1）得：△DBE≌△CFD，得出EB=DF，证出△ADF是等腰直角三角形，得出DF=AD，即可得出结果．                                                  【解答】（1）证明：作DF∥BC交AC于F，如图1所示：                  则∠ADF=∠ABC，∠AFD=∠ACB，∠FDC=∠DCE，                          ∵△ABC是等腰三角形，∠A=60°，                                ∴△ABC是等边三角形，                                          ∴∠ABC=∠ACB=60°，                                        ∴∠DBE=120°，∠ADF=∠AFD=60°=∠A，                          ∴△ADF是等边三角形，∠DFC=120°，                             ∴AD=DF，                                                   ∵∠DEC=∠DCE，                                             ∴∠FDC=∠DEC，ED=CD，                                         在△DBE和△CFD中，，                       \n∴△DBE≌△CFD（AAS），                                         ∴EB=DF，                                                   ∴EB=AD；                                                   （2）解：EB=AD成立；理由如下：                                 作DF∥BC交AC的延长线于F，如图2所示：                        同（1）得：AD=DF，∠FDC=∠ECD，∠FDC=∠DEC，ED=CD，                又∵∠DBE=∠DFC=60°，                                         ∴在△DBE和△CFD中，，                        ∴△DBE≌△CFD（AAS），                                         ∴EB=DF，                                                   ∴EB=AD；                                                   （3）解： =；理由如下：                                   作DF∥BC交AC于F，如图3所示：                                同（1）得：△DBE≌△CFD（AAS），                               ∴EB=DF，                                                   ∵△ABC是等腰直角三角形，DF∥BC，                              \n∴△ADF是等腰直角三角形，                                      ∴DF=AD，                                                ∴=，                                                 ∴=．                                                                                                                                                   【点评】本题是三角形综合题目，考查了等边三角形的判定与性质、全等三角形的判定与性质、等腰三角形的判定与性质、等腰直角三角形的判定与性质、平行线的性质等知识；本题综合性强，有一定难度，证明三角形全等是解决问题的关键．                                        　                                                          \n8、【分析】（1）根据矩形的性质和勾股定理得到AC=10，①当AP=PO=t，如图1，过P作PM⊥AO，根据相似三角形的性质得到AP=t=，②当AP=AO=t=5，于是得到结论；（2）作EH⊥AC于H，QM⊥AC于M，DN⊥AC于N，交QF于G，根据全等三角形的性质得到CE=AP=t，根据相似三角形的性质得到EH=，根据相似三角形的性质得到QM=，FQ=，根据图形的面积即可得到结论，（3）根据题意列方程得到t=，t=0，（不合题意，舍去），于是得到结论；（4）由角平分线的性质得到DM=DN=，根据勾股定理得到ON=OM==，由三角形的面积公式得到OP=5﹣t，根据勾股定理列方程即可得到结论．【解答】解：（1）∵在矩形ABCD中，Ab=6cm，BC=8cm，∴AC=10，①当AP=PO=t，如图1，过P作PM⊥AO，∴AM=AO=，∵∠PMA=∠ADC=90°，∠PAM=∠CAD，∴△APM∽△ADC，∴，∴AP=t=，②当AP=AO=t=5，∴当t为或5时，△AOP是等腰三角形；（2）作EH⊥AC于H，QM⊥AC于M，DN⊥AC于N，交QF于G，在△APO与△CEO中，，\n∴△AOP≌△COE，∴CE=AP=t，∵△CEH∽△ABC，∴，∴EH=，∵DN==，∵QM∥DN，∴△CQM∽△CDN，∴，即，∴QM=，∴DG=﹣=，∵FQ∥AC，∴△DFQ∽△DOC，∴，∴FQ=，∴S五边形OECQF=S△OEC+S四边形OCQF=×5×+（+5）•=﹣t2+t+12，∴S与t的函数关系式为S=﹣t2+t+12；（3）存在，∵S△ACD=×6×8=24，\n∴S五边形OECQF：S△ACD=（﹣t2+t+12）：24=9：16，解得t=，t=0，（不合题意，舍去），∴t=时，S五边形S五边形OECQF：S△ACD=9：16；（4）如图3，过D作DM⊥AC于M，DN⊥AC于N，∵∠POD=∠COD，∴DM=DN=，∴ON=OM==，∵OP•DM=3PD，∴OP=5﹣t，∴PM=﹣t，∵PD2=PM2+DM2，∴（8﹣t）2=（﹣t）2+（）2，解得：t≈15（不合题意，舍去），t≈2.88，∴当t=2.88时，OD平分∠COP．\n