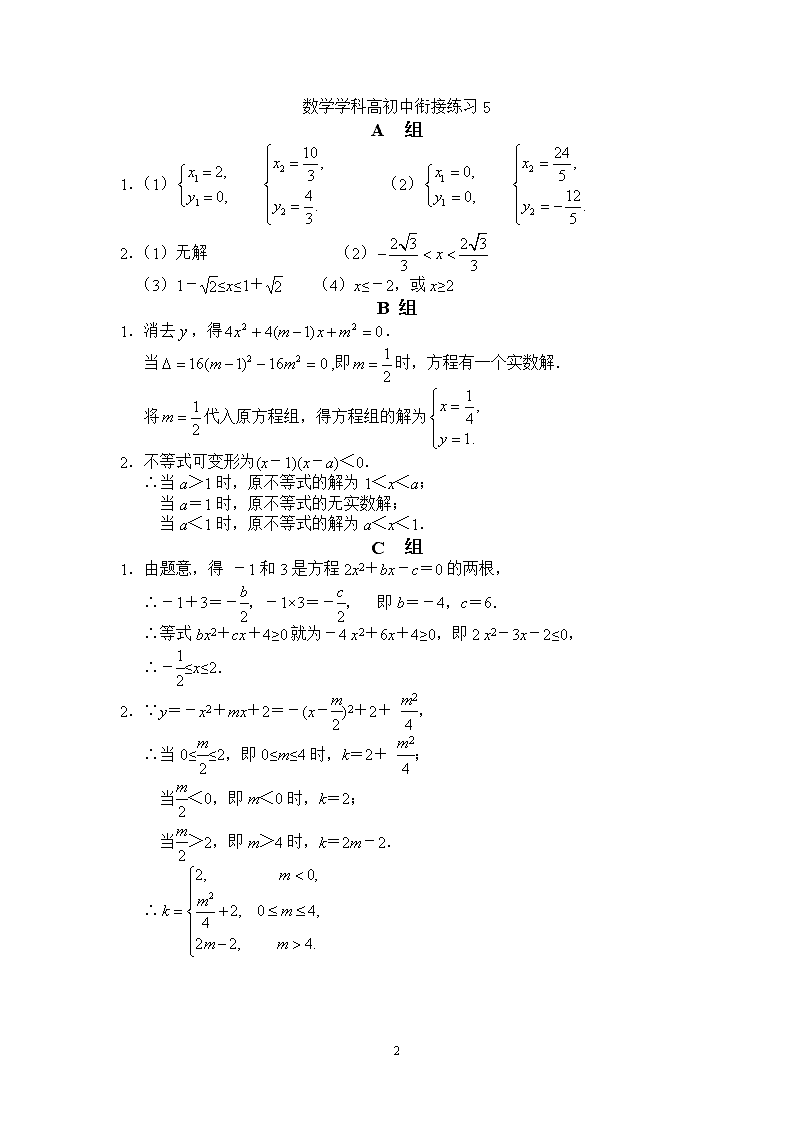数学学科高初中衔接练习5 2页

数学学科高初中衔接练习5A组1．解下列方程组：（1）（2）2．解下列不等式：（1）3x2－2x＋1＜0；（2）3x2－4＜0；（3）2x－x2≥－1；（4）4－x2≤0．B组1．取什么值时,方程组有一个实数解?并求出这时方程组的解．2．解关于x的不等式x2－(1＋a)x＋a＜0（a为常数）．C组1．已知关于x不等式2x2＋bx－c＞0的解为x＜－1，或x＞3．试解关于x的不等式bx2＋cx＋4≥0．2．试求关于x的函数y＝－x2＋mx＋2在0≤x≤2上的最大值k．2\n数学学科高初中衔接练习5A组1．（1）（2）2．（1）无解（2）（3）1－≤x≤1＋（4）x≤－2，或x≥2B组1．消去，得．当,即时，方程有一个实数解．将代入原方程组，得方程组的解为2．不等式可变形为(x－1)(x－a)＜0．∴当a＞1时，原不等式的解为1＜x＜a；当a＝1时，原不等式的无实数解；当a＜1时，原不等式的解为a＜x＜1．C组1．由题意，得－1和3是方程2x2＋bx－c＝0的两根，∴－1＋3＝－，－1×3＝－，即b＝－4，c＝6．∴等式bx2＋cx＋4≥0就为－4x2＋6x＋4≥0，即2x2－3x－2≤0，∴－≤x≤2．2．∵y＝－x2＋mx＋2＝－(x－)2＋2＋，∴当0≤≤2，即0≤m≤4时，k＝2＋；当＜0，即m＜0时，k＝2；当＞2，即m＞4时，k＝2m－2．∴2