初中数学总复习：《圆》基础练习题---副本 4页

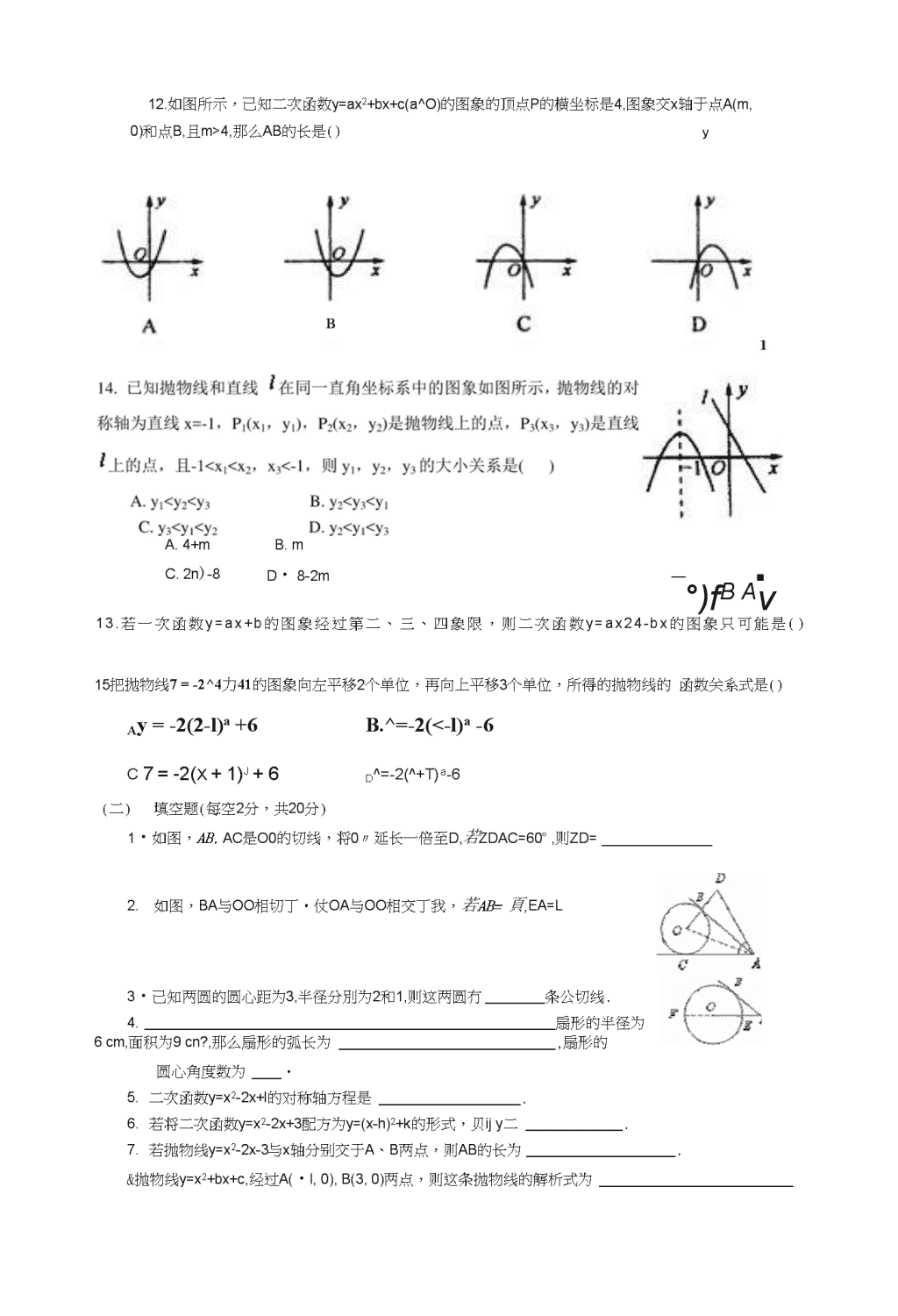
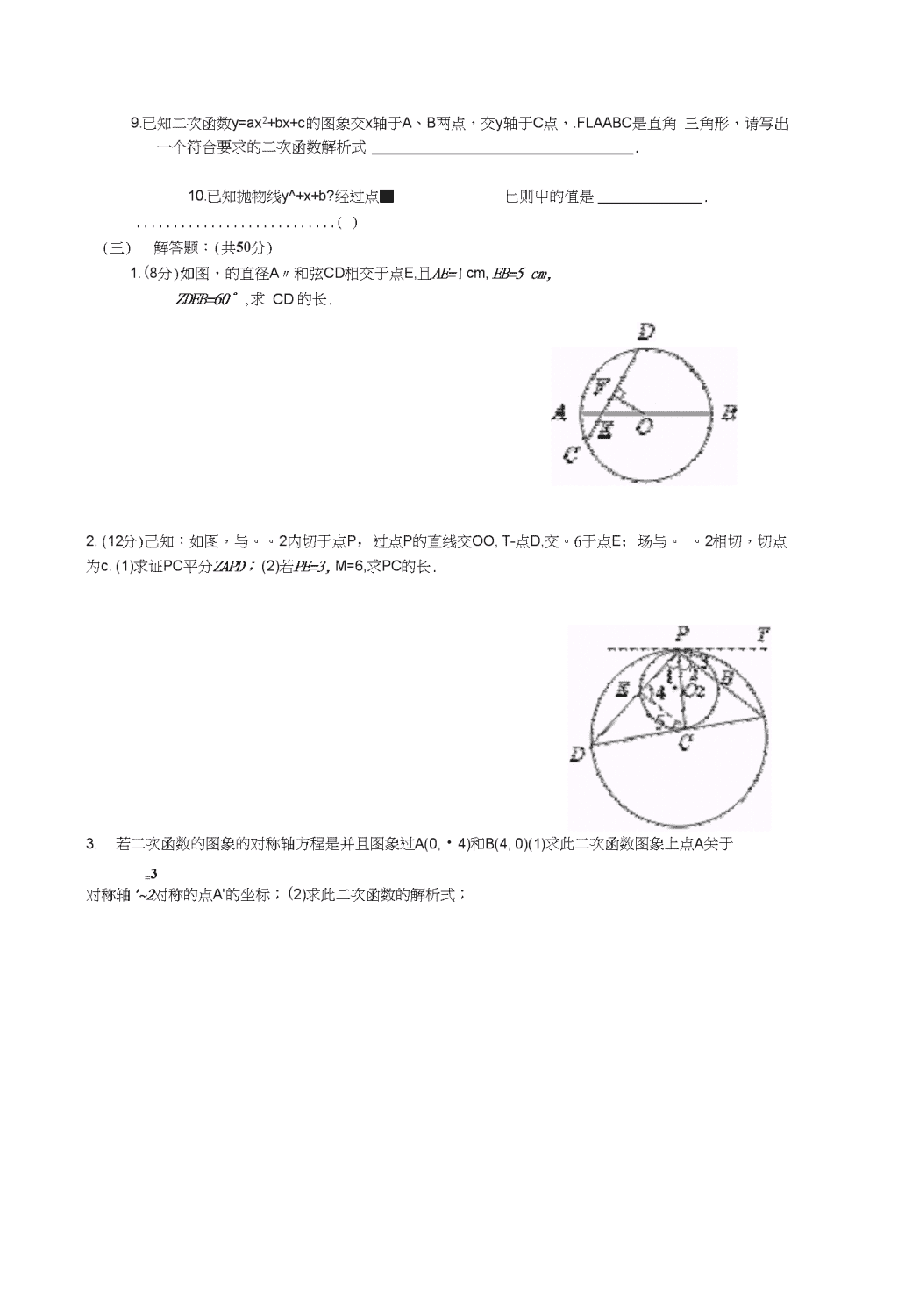
圆与二次函数基础练习题（一）选择题（每题2分，共30分）1.冇下列四个命题：①直径是弦；②经过三个点一定可以作圆；③三角形的外心到三角形各顶点的距离都相等；④半径相等的两个半岡是等弧.其中正确的有（）（A）4个（B）3个（C）2个（D）1个2.下列判断中正确的是（）（A）平分弦的頁线垂直于弦（B）平分弦的頁线也必平分弦所对的两条弧（C）弦的垂直平分线必平分弦所对的两条弧（D）平分一条弧的直线必平分这条弧所对的弦3.如图，在两半径不同的同心関中，ZAOB=ZArOB'=60°,则（）（A）ab=a;b,（B）（C）彳介的度数=於的度数5.6.8.圆内接四边形ABCD中，ZA、ZB、ZC的度数比是2：3：6,则ZD的度数是（（A）67.5°（B）135°（C）112.5°（D）110°04平分ZBOC,P是04上任一点，C不与点O巫合，且以P为圆心的圆与OC相离，那么圆P与OB的位置关系是（）（A）相离（B）相切（C）相交（D）不确定如图，已知四边形ABCD为圆内接四边形，AD为圆的直径，V3MN予G,且cosZABM=——,则tanZBCG的值为2(C)1(D)a/39.抛物线y=2（x-3）2的顶点在（）A・第一象限B.第二象限C.x轴上y=--xa-t-x-4io.抛物线4的对称轴是（A.x二2B.x二2C.x二4D.x=411.已知二次函数y=ax2+bx+c的图象如图所示，则下列结论中，JA.ab>0,c>0B.ab>0.c<0C-ab<0,c>0D.ab<0,c<0D.（D）行的长度=侖的长度\n12.如图所示，己知二次函数y=ax2+bx+c(a^O)的图象的顶点P的横坐标是4,图象交x轴于点A(m,0)和点B,且m>4,那么AB的长是()yBA.4+mC.2n)-8B.mD・8-2m—■°)fBAv13.若一次函数y=ax+b的图象经过第二、三、四象限，则二次函数y=ax24-bx的图象只可能是()15把抛物线7=-2^4力41的图象向左平移2个单位，再向上平移3个单位，所得的抛物线的函数关系式是()Ay=-2(2-l)a+6B.^=-2(<-l)a-6C7=-2(x+1)j+6D^=-2(^+T)a-6(二)填空题(每空2分，共20分)1・如图，AB.AC是O0的切线，将0〃延长一倍至D,若ZDAC=60°,则ZD=2.如图，BA与OO相切丁•仗OA与OO相交丁我，若AB=頁,EA=L3・己知两圆的圆心距为3,半径分別为2和1,则这两圆冇条公切线.1.扇形的半径为6cm,面积为9cn?,那么扇形的弧长为,扇形的圆心角度数为・2.二次函数y=x2-2x+l的对称轴方程是.3.若将二次函数y=x2-2x+3配方为y=(x-h)2+k的形式，贝ijy二.4.若抛物线y=x2-2x-3与x轴分别交于A、B两点，则AB的长为.&抛物线y=x2+bx+c,经过A(・l,0),B(3,0)两点，则这条抛物线的解析式为\n9.已知二次函数y=ax2+bx+c的图象交x轴于A、B两点，交y轴于C点，.FLAABC是直角三角形，请写出一个符合要求的二次函数解析式.10.已知抛物线y^+x+b?经过点■匕则屮的值是.()(二)解答题：(共50分)1.(8分)如图，的直径A〃和弦CD相交于点E,且AE=\cm,EB=5cm,ZDEB=60°,求CD的长.2.(12分)己知：如图，与。。2内切于点P，过点P的直线交OO,T-点D,交。6于点E；场与。。2相切，切点为c.(1)求证PC平分ZAPD；(2)若PE=3,M=6,求PC的长.2.若二次函数的图象的对称轴方程是并且图象过A(0,・4)和B(4,0)(1)求此二次函数图象上点A关于=3对称轴'~2对称的点A'的坐标；(2)求此二次函数的解析式；\n2.在直角坐标平血内，点0为坐标原点，二次函数y=x2+(k・5)x・(k+4)的图彖交x轴于点A(xP0).B(X2，0),.n.(X|+l)(x2+l)=-8.(1)求二次函数解析式；(2)将上述二次函数图象沿x轴向右平移2个单位，设平移后的图象与y轴的交点为C,顶点为P,求公POC的面积.5•已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A、另抛物线经过点(1，8),M为它的顶点.(1)求抛物线的解析式；(2)求Z\MCB的面积Samcb-B两点，其中A点坐标为(・1,0),点C(0,5),