中考数学试题按知识点分类汇编圆的有关计算 13页

知识点15：圆的有关计算 ‎（1）（2008年镇江市）11．圆柱的底面半径为1，母线长为2，则它的侧面积为 （结果保留）．‎ ‎（2）（2008年衢州）在半径为5的圆中，的圆心角所对的弧长为___.___(结果保留)‎ ‎ ‎ ‎（3）在（2008年衢州）半径为‎5cm的圆中，两条平行弦的长度分别为‎6cm和‎8cm，则这两条弦之间的距离为 ‎1cm或‎7cm ． ‎ ‎（4）（2008乌鲁木齐）如图4所示的半圆中，是直径，且，，‎ 则的值是 ．‎ ‎（5）（2008乌鲁木齐）如图5所示是一个圆锥在某平面上的正投影，则该圆锥的侧面积是 ．‎ ‎ ‎ ‎（6）（2008衢州）在半径为5的圆中，的圆心角所对的弧长为____._____‎ ‎(结果保留) ‎ ‎（7）（2008年辽宁省十二市）一个圆锥底面周长为cm，母线长为‎5cm，则这个圆锥的侧面积是 ． ‎ ‎（8）(2008年山西省太原市)已知圆锥的底面半径为‎2cm，母线长为‎4cm，则圆锥的侧面积为： cm2．‎ ‎（9）(2008年山西省太原市)如图，是的直径，是的弦，连接，‎ 若，则的度数为 ．‎ 答案:55°‎ ‎（10）（2008年遵义市）17．如图，梯形中，，，，，以为圆心在梯形内画出一个最大的扇形（图中阴影部分）的面积是 . ．‎ ‎ ‎ ‎ ‎ ‎（11）（2008年龙岩市）如图，量角器外沿上有A、B两点，它们的读数分别是70°、40°，则∠1的度数为 15° . 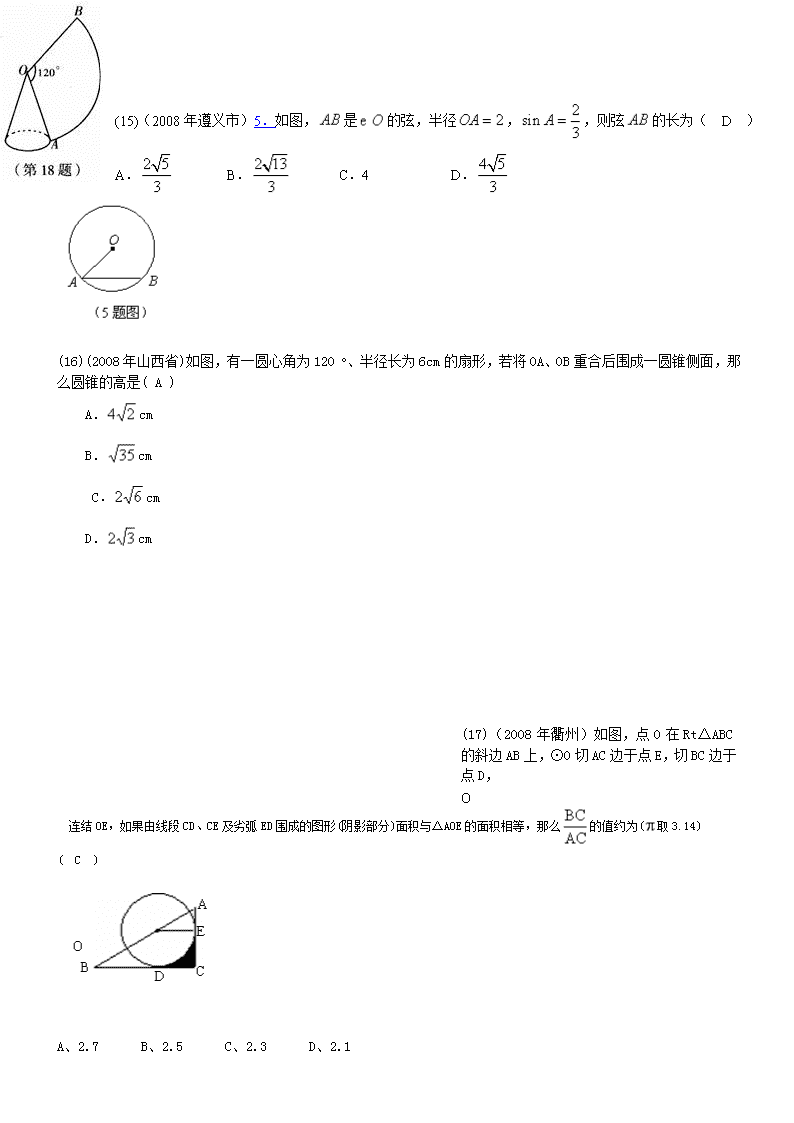‎ ‎▲‎ ‎ （12）（2008年江苏省迁宿市）用圆心角为，半径为的扇形做成一个无底的圆锥侧面则此圆锥的底面半径为：‎‎2cm ‎(13) (2008湖北省荆门)如图，将圆沿AB折叠后，圆弧恰好经过圆心，则( c ) 等于 ‎(A) 60°． (B) 90°． (C)120°． (D)150°．‎ ‎(13)（湖南邵阳）计算机把数据存储在磁盘上，磁盘上有一些同心圆转道．如图（九），现有一张半径为45毫米的磁盘，磁盘的最内磁道半径为毫米，磁盘的最外圆周不是磁道，磁道上各磁道之间的宽度必须不小于0.3毫米，这张磁盘最多有 条磁道．‎ ‎(14)（湖南常德）小红量得一个圆锥的母线长为15㎝，底面圆的直径是6㎝,它的侧面积为 45π㎝2(结果保留π).‎ ‎(15)（2008年遵义市）5．如图，是的弦，半径，，则弦的长为（ D ）‎ A． B． C．4 D．‎ ‎(16)(2008年山西省)如图，有一圆心角为120 o、半径长为‎6cm的扇形，若将OA、OB重合后围成一圆锥侧面，那么圆锥的高是( A )‎ A．cm ‎ B．cm ‎ ‎ C．cm ‎ D．cm ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎(17)（2008年衢州）如图，点O在Rt△ABC的斜边AB上，⊙O切AC边于点E，切BC边于点D，‎ O ‎ 连结OE，如果由线段CD、CE及劣弧ED围成的图形(阴影部分)面积与△AOE的面积相等，那么的值约为(取3.14) ( C )‎ ‎ ‎ ‎ ‎ A、2.7 B、‎2.5 C、2.3 D、2.1‎ ‎(18) （2008年衢州）一个圆锥侧面展开图的扇形的弧长为，则这个圆锥底面圆的半径为（ A ）‎ A． B． ‎ C． D．‎ ‎(19)（08眉山）如图，等边的边长为‎12cm，内切切边于点，则图中阴影部分的面积为（ A ）‎ A． B． ‎ C．2 D．‎ ‎(21)(2008年南通市)在一次数学探究型学习活动中，某学习小组要制作一个圆锥体模型，操作规则是：在一块边长为‎16cm的正方形制片上剪出一个扇形和一个圆，使得扇形围成圆锥的侧面时，圆恰好是该圆锥的底面.它们首先设计了如图所示的方案一，发现这种方案不可行，于是他们调整了扇形和圆的半径，设计了如图所示的方案二.（两个方案的图中，圆与正方形相邻两边及扇形的弧均相切.方案一中扇形的弧与正方形的两边相切）‎ ‎（1）请说明方案一不可行的理由；‎ ‎（2）判断方案二是否可行？若可行，请确定圆锥的母线长及其底面圆半径；若不可行，请说明理由.‎ ‎ 方案一 方案二 解：（1）理由如下：‎ ‎∵扇形的弧长＝16×＝8π，圆锥底面周长＝2πr，∴圆的半径为‎4cm.‎ 由于所给正方形纸片的对角线长为16cm，而制作这样的圆锥实际需要正方形直劈昂的对角线长为16＋4＋4＝（20＋4）cm，20＋4＞16，‎ ‎∴方案一不可行.‎ ‎（2）方案二可行.求解过程如下：‎ 设圆锥底面圆的半径为rcm，圆锥的母线长为Rcm，则 ‎，① 2πr＝.②‎ 由①②可得，r＝.‎ 故所求圆锥的母线长为cm，底面圆的半径为cm.‎ ‎(22)（2008乌鲁木齐）．如图9，在平面直角坐标系中，以点为圆心，2为半径作圆，交轴于两点，开口向下的抛物线经过点，且其顶点在上．‎ ‎（1）求的大小；‎ ‎（2）写出两点的坐标；‎ ‎（3）试确定此抛物线的解析式；‎ ‎（4）在该抛物线上是否存在一点，使线段与互相平分？若存在，求出点的坐标；若不存在，请说明理由．‎ 解：（1）作轴，为垂足，‎ ‎，半径 ‎，‎ ‎（2），半径 ‎，故 ‎（3）由圆与抛物线的对称性可知抛物线的顶点的坐标为 设抛物线解析式 把点代入上式，解得 ‎（4）假设存在点使线段与互相平分，则四边形是平行四边形 且．‎ 轴，点在轴上 又，，即．‎ 又满足，‎ 点在抛物线上 所以存在使线段与互相平分 ‎(23)（2008年辽宁省十二市）20.如图10，为的直径，为弦的中点，连接并延长交于点，与过点的切线相交于点．若点为的中点，连接．‎ 求证：．‎ ‎.解析：本题主要考查圆的有关知识及三角形全等的判定方法的掌握，一定要充分运用圆的相关知识，得到相等的线段和角，然后根据三角形全等的判定方法进行判定即可.‎ 解：（1）证明：如图2．‎ 是的直径．‎ 又是的切线，‎ 过圆心，，‎ ‎．‎ 为中点，‎ ‎．‎ ‎(24)（2008年贵阳市）如图10，已知是的直径，点在上，且，．‎ ‎（1）求的值．（3分）‎ ‎（2）如果，垂足为，求的长．（3分）‎ ‎（3）求图中阴影部分的面积（精确到0.1）．（4分）‎ 答案：（1）AB是⊙O的直径，点C在⊙O上 ‎∠ACB = 90o ‎ AB＝13，BC＝5‎ ‎．‎ ‎（2）在Rt△ABC中，‎ ‎．‎ ‎，‎ ‎．‎ ‎（3）（平方单位）‎ ‎ ‎ ‎(25)（2008陕西）如图，在中，，，，是的角平分线．过三点的圆与斜边交于点，连接．‎ ‎（1）求证：；‎ ‎（2）求外接圆的半径．‎ ‎（1）证明：，为直径 又是的角平分线，‎ ‎，．‎ ‎（2）解：，‎ ‎．‎ ‎，．‎ 为直径，．‎ ‎，‎ ‎．．‎ ‎．‎ 外接圆的半径为 ‎(26)（2008年龙岩市）如图，在平面直角坐标系xOy中，⊙O交x轴于A、B两点，直线FA⊥x轴于点A，点D在FA上，且DO平行⊙O的弦MB，连DM并延长交x轴于点C.‎ ‎（1）判断直线DC与⊙O的位置关系，并给出证明；‎ ‎（2）设点D的坐标为（-2，4），试求MC的长及直线DC的解析式.‎ 答案：（1）答：直线DC与⊙O相切于点M .‎ ‎ 证明如下：连OM， ∵DO∥MB， ‎ ‎ ∴∠1=∠2，∠3=∠4 .‎ ‎ ∵OB=OM，‎ ‎ ∴∠1=∠3 .‎ ‎ ∴∠2=∠4 . ‎ ‎ 在△DAO与△DMO中，‎ ‎ ‎ ‎ ∴△DAO≌△DMO . ∴∠OMD=∠OAD .‎ ‎ 由于FA⊥x轴于点A，∴∠OAD=90°.‎ ‎ ∴∠OMD=90°. 即OM⊥DC ‎ ‎ ∴DC切⊙O于M.‎ ‎ （2）解：由D（－2，4）知OA=2（即⊙O的半径），AD=4 ‎ ‎ 由（1）知DM=AD=4，由△OMC∽△DAC，知= = = .‎ ‎ ∴AC=2MC. ‎ ‎ 在Rt△ACD中，CD=MC＋4.‎ ‎ 由勾股定理，有(2MC)2＋42=(MC＋4)2，解得MC= 或MC=0（不合，舍去）.‎ ‎ ∴MC的长为. ‎ ‎ ∴点C（，0）. ‎ ‎ 设直线DC的解析式为y = kx＋b ‎ 则有 ‎ 解得 ‎ ‎ ∴直线DC的解析式为 y =－x＋. ‎ ‎.‎ ‎(27)（2008年江苏省迁宿市）如图，⊙的直径是，过点的直线是⊙的切线，、是⊙上的两点，连接、、和．‎ ‎(1)求证：；‎ ‎(2)若是的平分线，且，求的长．‎ 参考答案：23．(1)证明: ∵是⊙的直径 ‎∴‎ ‎∵切⊙于点 ‎∴‎ ‎∴‎ ‎∵‎ ‎∴.‎ ‎(2) 如右图,连接,过点作于点.‎ ‎∵平分 ‎∴‎ ‎∴弧弧 ‎∵是⊙的直径 ‎∴‎ 又∵‎ ‎∴‎ ‎∵‎ ‎∴‎ ‎∵‎ ‎∴‎ ‎∴.‎ ‎ (28)(2008年厦门市)已知：如图，中，，以为直径的交于点，于点．‎ ‎（1）求证：是的切线；‎ ‎（2）若，求的值．‎ ‎（1）证明：，‎ 又，‎ 又于，，‎ 是的切线 ‎（2）连结，是直径，‎ ‎，，‎ ‎(29) （湖南邵阳）如图（十六），正方形的边长为1，以为圆心、为半径作扇形与相交于点，设正方形与扇形之间的阴影部分的面积为；然后以为对角线作正方形，又以为圆心，、为半径作扇形，与相交于点，设正方形与扇形之间的阴影部分面积为；按此规律继续作下去，设正方形与扇形之间的阴影部分面积为．‎ ‎（1）求；‎ ‎（2）写出；‎ ‎（3）试猜想（用含的代数式表示，为正整数）．‎ 解：（1）‎ ‎（2）‎ ‎（3）（为正整数）．‎