中考圆与四边形综合题 14页

中考圆与四边形难题解析 ◆考点分析 特殊四边形主要包括梯形、平行四边形、矩形、菱形、正方形等，中考中有关考题大 多以容易题或中档题为主，因此更多体现了对基础知识的考查。近年的中考题中也出现了 一些探究题、折痕问题、图形变换问题等新题型。 圆是初中几何的重要学习内容，它具有很多主要性质，知识的前后联系密切，能考查 学生综合应用数学知识的能力，是历年中考的重点。主要包括以下几种类型：圆的有关性 质的考查，以基础题为主；圆与三角形的有关知识（全等、相似等）相联系的题型，此类 试题要求通过圆的有关性质得出两个三角形对应角相等或对应边相等或成比例，进而证明 三角形全等或相似；考查与圆有关的位置关系的掌握情况，这类问题考查的重点是相切关 系的性质和判定，试题常由课本习题改编而成，解答时需要合理联想课本习题原型；圆与 函数和方程相联系，这类题需综合函数、方程、几何的相关知识，融计算、证明于一体， 具有较强的综合性；圆与特殊四边形相联系这类题主要是计算弧长、扇形面积、阴影部分 面积等。 ◆典型例题 例 1 （2007 芜 湖 ） 已知多边形 ABDEC 是由边长为 2 的等边三角形 ABC 和正方形 BDEC 组成，一圆过 A、D、E 三点，求该圆半径的长． 【解题分析】 本题有机的将等边三角形、正方形、圆融合在一道题中. 解法一．如图 2.1-1，将正方形 BDEC 上的等边△ABC 向下平移得 等边△ODE，其底边与 DE 重合．得出 OD =OA=OE 即可。 解法二．如图 2，作 AF⊥BC，垂足为 F，并延长交 DE 于 H 点． 设⊙O 的半径为 r，可得方程 2 2 2(2 3 ) 1r r    ． 解得ｒ＝2． ∴该圆的半径长为 2. 【每题一得】 利用等边三角形、正方形、圆的轴对称性是解决 问题的关键。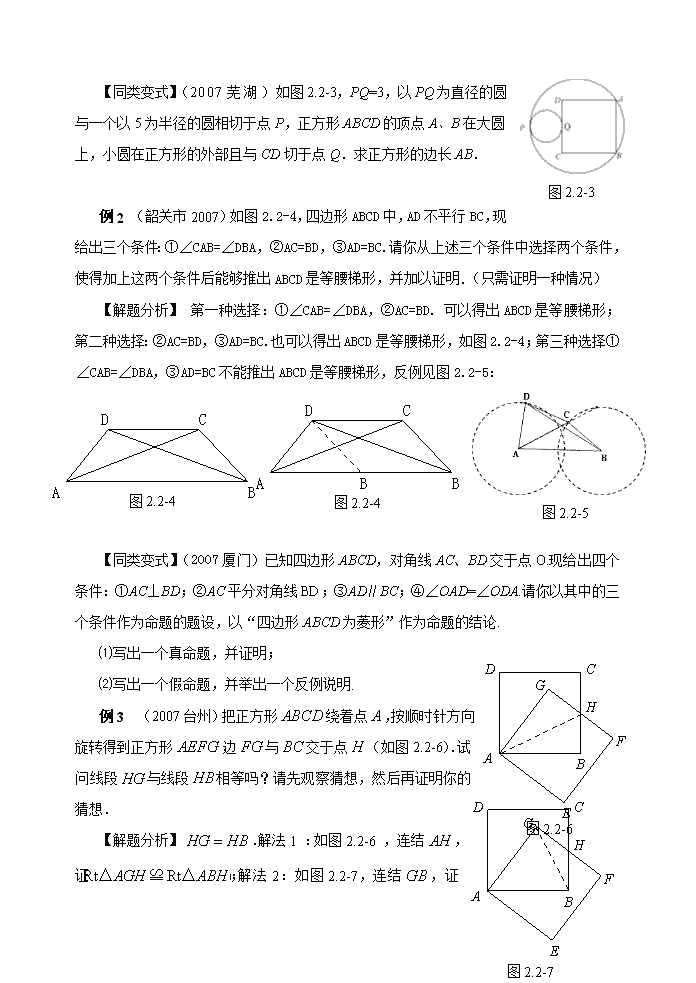 图 2.2-1 图 2.2-2 【同类变式】（2007 芜 湖 ） 如图 2.2-3，PQ=3，以 PQ 为直径的圆 与一个以 5 为半径的圆相切于点 P，正方形 ABCD 的顶点 A、B 在大圆 上，小圆在正方形的外部且与 CD 切于点 Q．求正方形的边长 AB． 例 2 （韶关市 2007）如图 2.2-4，四边形 ABCD 中，AD 不平行 BC， 现给出三个条件：①∠CAB=∠DBA，②AC=BD，③AD=BC.请你从上述三个条件中选择两个条 件，使得加上这两个条件后能够推出 ABCD 是等腰梯形，并加以证明.（只需证明一种情况） 【解题分析】 第一种选择：①∠CAB=∠DBA，②AC=BD. 可以得出 ABCD 是等腰梯形； 第二种选择：②AC=BD，③AD=BC.也可以得出 ABCD 是等腰梯形，如图 2.2-4；第三种选择 ①∠CAB=∠DBA，③AD=BC 不能推出 ABCD 是等腰梯形，反例见图 2.2-5： 【同类变式】（2007 厦门）已知四边形 ABCD，对角线 AC、BD 交于点 O.现给出四个 条件：①AC⊥BD；②AC 平分对角线 BD；③AD∥BC；④∠OAD=∠ODA.请你以其中的三 个条件作为命题的题设，以“四边形 ABCD 为菱形”作为命题的结论. ⑴写出一个真命题，并证明； ⑵写出一个假命题，并举出一个反例说明. 例 3 （2007 台州）把正方形 ABCD 绕着点 A ，按顺时针方 向旋转得到正方形 AEFG ，边 FG 与 BC 交于点 H （如图 2.2-6）．试问线段 HG 与线段 HB 相等吗？请先观察猜想，然后再 证明你的猜想． 【解题分析】 HG HB ．解法 1：如图 2.2-6，连结 AH ， 证Rt Rt ( )AGH ABH HL △ ≌ △ ；解法 2：如图 2.2-7，连结GB ，证 图 2.2-3 D C BA 图 2.2-4 D C BA B 图 2.2-4 图 2.2-5 D C A B G H F E 图 2.2-6 D C A B G H F E 图 2.2-7 HGB HBG  ∴ ． 【每题一得】图形的折叠、旋转、平移等相关的考题越来越多地出现在各地的考题中， 关注图形的变换规律的探究是值得关注的考试动向。 【同类变式】（2007 扬州）如图 2.2-8，正方形 ABCD 绕点 A 逆时针旋转 n 后得到正 方形 AEFG ，边 EF 与 CD 交于点O ． （1）以图中已标有字母的点为端点连结两条线段（正方形 的对角线除外），要求所连结的两条线段相交且互相垂直．．．．．．．，并说 明这两条线段互相垂直的理由； （2）若正方形的边长为 2cm ，重叠部分（四边形 AEOD ） 的面积为 24 3 cm3 ，求旋转的角度 n ． 例4 (2007天津)如图2.2-8，AD是圆O的直径，BC切圆O于点D，AB、AC与圆O相交 于点E、F。 ⑴求证： ACAFABAE  ； ⑵如果将图①中的直线BC向上平移与圆O相交得图②，或向下平移得图③，此时， ACAFABAE  是否仍成立？若成立，请证明，若不成立，说明理由。 图 2.2-8 图 2.2-9 图 2.2-10 【解题分析】解：（1）如图 2.2-8，连接 DE，连接 DF 证 AEDRt ～ ADBRt ， AFDRt ～ ADCRt ，分别得到 2ADABAE  ， 2ADACAF  。（2）两种情况下 仍然通过证明相似可知结论依然成立. G D O C F E BA 图 2.2-8 【每题一得】与圆有关的运动变化探究性题型体现了很强的综合性，同时也渗透着数 形结合、分类、运动变化等诸多的数学思想方法，并且在实际生活中也有着广泛的应用， 所以综合运用所学知识解答以圆为背景的试题也是近年来各地中考的热点题型。 【同类变式】(2007 潍坊) 如图 2.2-11，线段 PB 过圆心O ，交圆O 于 A B， 两点，PC 切圆 O 于点 C ，作 AD PC ，垂足为 D ，连结 AC BC， ． （1）写出图 1 中所有相等的角（直角除外），并给出证明； （2）若图 1 中的切线 PC 变为图 2.2-12 中割线 PCE 的情形，PCE 与圆O 交于C E， 两点， AE 与 BC 交于点 M ， AD PE ，写出图 2 中相等的角（写出三组即可，直角除 外）； （3）在图 2.2-12 中，证明： AD·AB=AC·AE． ◆当堂反馈 1．（2007 临沂）如图，在四边形 ABCD 中，E、F、G、H 分别是 AB、BD、CD、AC 的中点，要使四边形 EFGH 是菱形，四边 形 ABCD 还应满足的一个条件是 。 2．（2007 重庆）已知，如图 2.2-14：AB 为⊙O 的直径，AB＝AC，BC 交⊙O 于点 D，AC 交⊙O 于点 E，∠BAC＝450。给出以下五个结论： ①∠EBC＝22.50，；②BD＝DC；③AE＝2EC；④劣弧  AE 是劣弧  DE 的 2 倍；⑤AE＝BC。其中正确结论的序号是 。 3．（2007 资阳）如图 2.2-15，已知 P 为正方形 ABCD 的对角线 AC 上一点(不与 A、C 重合)， PE⊥BC 于点 E，PF⊥CD 于点 F. (1) 求证：BP=DP； (2) 如图 2.2-16，若四边形 PECF 绕点 C 按逆时针方向旋转，在旋转过程中是否总有 BP=DP？若是，请给予证明；若不是，请用反例加以说明； A B CP D O 图 2.2-11 A B CP D O M E 图 2.2-12 A E C B D G H F 图 2.2-13 图 2.2-14 (3) 试选取正方形 ABCD 的两个顶点，分别与四边形 PECF 的两个顶点连结，使得 到的两条线段在四边形 PECF 绕点 C 按逆时针方向旋转的过程中长度始终相等，并证明 你的结论 . 4．（2007 福州）如图 8，已知： ABC△ 内接于 O ， 点 D 在OC 的延长线上， 1sin 2B  ， 30D   ． （1）求证： AD 是 O 的切线； （2）若 6AC  ，求 AD 的长． ◆配套练习 一、选择题 1．（2007 东营）如图 2，四边形 ABCD 为矩形纸片．把纸片 ABCD 折叠，使点 B 恰好落在 CD 边的中点 E 处，折痕为 AF．若 CD＝6，则 AF 等于 （ ） A． 34 B． 33 C． 24 D．８ 2．（2007 金华）国家级历史文化名城——金华，风光秀丽，花木葱茏．某广场上一个形状 是平行四边形的花坛（如图），分别种有红、黄、蓝、绿、橙、紫 6 种颜色的花．如果 有 AB EF DC∥ ∥ ， BC GH AD∥ ∥ ，那么下列说法中错误的是（ ） A．红花、绿花种植面积一定相等； B．紫花、橙花种植面积一定相等 C．红花、蓝花种植面积一定相等； D．蓝花、黄花种植面积一定相等 3．（2007 内江）如图 2.2-20，这是中央电视台“曲苑杂谈”中的一副图案，它是一扇形图 形，其中 AOB 为120 ，OC 长为 8cm，CA 长为 12cm，则阴影部分的面积为（ ） A． 264πcm ；B． 2112πcm ；C． 2144πcm ；D． 2152πcm 图 2.2-16图 2.2-15 图 2.2-17 二、填空题 4．（2007 成都）如图 2.2-21，把一张矩形纸片 ABCD 沿 EF 折叠后，点 C D， 分别落在 C D ， 的位置上，EC 交 AD 于点G ．已知 58EFG  °，那么 BEG  °． 5．（2007 成都）如图 2.2-22，已知 AB 是⊙O 的直径，弦CD AB ， 2 2AC  ， 1BC  ， 那么sin ABD 的值是 ． 6．（2007 济宁）如图 2.2-23，从 P 点引⊙O 的两切线 PA、PA、PB，A、B 为切点，已知 ⊙O 的半径为 2，∠P＝60°，则图中阴影部分的面积为 。 7．（2007 枣庄）如图 2.2-24，AB 是⊙O 的直径，BC 是弦，OD⊥BC 于 E，交弧 BC 于 D． (1) 请写出五个不同类型的正确结论； (2) 若 BC=8，ED＝2，求⊙O 的半径． 8．（2007 河池）如图 2.2-25，半圆 O 为△ABC 的外接半圆，AC 为直径，D 为弧 BC 上的 一动点．⑴ 问添加一个什么条件后，能使得 BD BE BC BD  ？请说明理由； ⑵ 若 AB∥OD，点 D 所在的位置应满足什么条件？请说明理由； ⑶ 如图 2.2-26，在⑴和⑵的条件下，四边形 AODB 是什么特殊的四边形？证明你的结 论． A C O B 图 2.2-20 图 2.2-24 图 2.2-19图 2.2-18 图 2.2-23图 2.2-21 图 2.2-22 B A O C E · 图 2.2-25 D 图 2.2-26 9．（2007 常州）如图 2.2-27，菱形、矩形与正方形的形状有差异，我们将菱形、矩形与 正方形的接近程度称为“接近度”．在研究“接近度”时，应保证相似图形的“接近度” 相等． ⑴ 设菱形相邻两个内角的度数分别为 m 2 和 n2，将菱形的“接 近度”定义为|m－n|，于是，|m－n|越小，菱形越接近于正方形． ①若菱形的一个内角为 70°，则该菱形的“接近度”等 于 ； ②当菱形的“接近度”等于 时，菱形是正方形． ⑵ 设矩形相邻两条边长分别是 a 和 b （ a b≤ ），将矩形的 “接近度”定义为|a－b|，于是|a－b|越小，矩形越接近于正方 形．你认为这种说法是否合理？若不合理，给出矩形的“接近度”一个合理定义． 10．（2007 南充）如图 2.2-28 是某城市一个主题雕塑的平面示意图，它由置放于地面 l 上 两个半径均为 2 米的半圆与半径为 4 米的⊙A 构成．点 B、C 分别是两个半圆的圆心， ⊙A 分别与两个半圆相切于点 E、F，BC 长为 8 米．求 EF 的长． 图 2.2-27 a b n m A E F l B C图 2.2-28 答案: 【典型例题】 例 1 解:方法一．如图 1，将正方形 BDEC 上的等边△ABC 向下平移得等边△ODE，其底边 与 DE 重合． ∵A、B、C 的对应点是 O、D、E． ∴OD=AB，OE=AC，AO=BD． ∵等边△ABC 和正方形 BDEC 的边长都是 2， ∴AB=BD=AC=2． ∴OD =OA=OE=2． ∵A、D、E 三点不在同一直线上， ∴A、D、E 三点确定一圆， ∵O 到 A、D、E 三点的距离相等， ∴O 点为圆心，OA 为半径． ∴该圆的半径长为 2． 方法二．如图 2，作 AF⊥BC，垂足为 F，并延长交 DE 于 H 点． ∵△ABC 为等边三角形， ∴AF 垂直平分 BC， ∵四边形 BDEC 为正方形， ∴AH 垂直平分正方形的边 DE． 又 DE 是圆的弦，∴AH 必过圆心，记圆心为 O 点，并设⊙O 的半径为 r． 在 Rt△ABF 中， ∵∠BAF= °30 ， ∴ ° 3cos30 2 32AF AB     ． ∴OH= AF FH OA  = 3 2 ｒ． 图 1 图 2 在 Rt△ODH 中， 2 2 2OH DH OD  ． ∴ 2 2 2(2 3 ) 1r r    ．解得ｒ＝2． ∴该圆的半径长为 2． 【同类变式】6 例 2 第一种选择：①∠CAB=∠DBA，②AC=BD. 证明：∵∠CAB=∠DBA，AC=BD，AB=BA ∴△ACB≌△BDA ∴AD=BC，∠ABC=∠BAD 作 DE∥BC 交 AB 于 E，如图（3），则∠DEA=∠CBA ∴∠DAE=∠DEA，AD=ED ∴AB∥CD 又∵AD 不平行 BC，∴ABCD 是等腰梯形 第二种选择：②AC=BD，③AD=BC. 证明：延长 AD、BC 相交于 E，如图（2） ∵AC=BD，AD=BC,AB=BA, ∴△DAB≌△CBA ∴∠DAB=∠CBA ∴EA=EB 又 AD=BC，∴DE=CE，∠EDC=∠ECD 而，∠E+∠EAB+∠EBA=∠E+∠EDC+∠ECD ∴∠EDC=∠EAB ∴DC∥AB D C BA 图 3 B D C BA 图 4 E BA C D 图 5 又∵AD 不平行 BC，∴ABCD 是等腰梯形 说明：由①、③不能推出 ABCD 是等腰梯形，反例见图 5： 例 3 HG HB ． 证法 1：如图 6，连结 AH ， ∵四边形 ABCD ， AEFG 都是正方形．  90B G    °． 由题意知 AG AB ，又 AH AH ． Rt Rt ( )AGH ABH HL △ ≌ △ ， HG HB∴ ． 证法 2：如图 7，连结GB ． ∵四边形 ABCD AEFG， 都是正方形， 90ABC AGF   ∴ °． 由题意知 AB AG ． AGB ABG  ∴ ． HGB HBG  ∴ ． HG HB∴ ． 【同类变式】 解：（1）如图 8，我连结的两条相交且互相垂直的线段是 AO 和 DE． AO DE 理由如下： 证明： 在 Rt ADO△ 与 Rt AEO△ 中， AD AE AO AO ， ， Rt RtADO AEO △ ≌ △ ， DAO OAE   （即 AO 平分 DAE ） AO DE  （等腰三角形的三线合一） 注：其它的结论也成立如GD BE⊥ ． （2）旋转的角度 n 为30 D C A B G H F E 图 7 G D O C F E BA 图 8 四边形 AEOD 的面积为 4 3 3 ， 三角形 ADO 的面积 2 3 2 3 AD DO  ， 2 32 3AD DO  ， ， 30 30DAO EAB    ， ． 例4 解：（1）如图9，连接DE ∵ AD 是圆 O 的直径 ∴ ∠AED=90° 又∵ BC 切圆 O 于点 D ∴ AD⊥BC，∠ADB=90° 在 AEDRt 和 ADBRt 中，∠EAD=∠DAB ∴ AEDRt ～ ADBRt ∴ AB AD AD AE  ，即 2ADABAE  同理连接 DF，可证 AFDRt ～ ADCRt ， 2ADACAF  ∴ ACAFABAE  （2） ACAFABAE  仍然成立 如图 10，连接 DE，因为 BC 在上下平移时始终与 AD 垂直，设垂足为 D 则 90 BDA ∵ AD 是圆 O 的直径 ∴ ∠AED=90° 又∵ EADABD  ∴ BDARt  ～ AEDRt ∴ AE DA AD AB  ADDAABAE  同理 ADDAACAF  ∴ ACAFABAE  图 9 图 10 同理可证，当直线 BC 向下平移与圆 O 相离如图③时， ACAFABAE  仍然成立。 【同类变式】（1）图 11 中相等的角有： ACD ABC BAC CAD     ， ． 证明：连结OC ，则OC PC⊥ ， AD PC ⊥ ， AD OC ∥ ， CAD OCA   ，又OA OC ， BAC OCA   ， BAC CAD   ．又 AB 为直径， 90 90ACB BAC B      ， ， 90CAD ACD ACD ABC       ， ． （2） ACD ABE ABC AEC BAE BCE        ， ， ， BEA BCA CBE CAE     ， （三组即可） （3）图 12 中易证 ADC AEB△ ∽△ ， AD AC AD AB AC AEAE AB     ， ． ◆当堂反馈 1．答案：AD＝BC，或 ABCD 为等腰梯形（答案不唯一） 2．①②④； 3．⑴ 解法一：在△ABP 与△ADP 中，利用全等可得 BP=DP. 解法二：利用正方形的轴对称性，可得 BP=DP. ⑵ 不是总成立 .当四边形 PECF 绕点 C 按逆时针方向旋转，点 P 旋转到 BC 边上时， DP >DC>BP，此时 BP=DP 不成立. ⑶ 连接 BE、DF，则 BE 与 DF 始终相等. 可证四边形 PECF 为正方形， 在△BEC 与△DFC 中，可证△BEC≌△DFC . 从而有 BE=DF 4．（1）证明：如图 13，连结OA． 1sin 2B ∵ ， 30B ∴ °． 2AOC B  ∵ ， 60AOC ∴ °． 图 11 A B CP D O 图 12 A B CP D O M E A C D B O 图 13 30D ∵ °， 180 90OAD D AOD    ∴ ° °． AD∴ 是⊙O 的切线． （2）解： OA OC∵ ， 60AOC  °． AOC∴△ 是等边三角形， 6OA AC ∴ ． 90OAD ∵ °， 30D  °， 3 6 3AD AO ∴ ． ◆配套练习 一、选择题 1．A； 2．C； 3．B； 二、填空题 4．64； 5． 2 2 3 ； 6．4 3 － 4 3  7．解：(1)不同类型的正确结论有： ①BC=CE ;②  BD CD ③∠BED=90°④∠BOD=∠A;⑤AC∥OD，⑥AC⊥BC; ⑦OE2+BE2=OB2;⑧S△ABC＝BC·OE;⑨△BOD 是等腰三角形， ⑩△BOE∽△BAC;等 (2)∵OD⊥BC， ∴BE＝CE= 1 2 BC=4． 设⊙O 的半径为 R，则 OE=OD-DE=R-2． 在 Rt△OEB 中，由勾股定理得 OE2＋BE2=OB2，即(R-2)2＋42=R2． 解得 R＝5．∴⊙O 的半径为 5． 8．（1）添加 AB=BD ∵AB=BD ∴ AB = BD ∴∠BDE =∠BCD 又∵∠DBE =∠DBC ∴△BDE∽△BCD ∴ BD BE BC BD  （2）若 AB∥DO，点 D 所在的位置是 BC 的中点 ∵AB∥DO ∴∠ADO =∠BAD ∵∠ADO =∠OAD ∴∠OAD =∠BAD ∴ DB = DC （3）在（1）和（2）的条件下，． ∵ AB = BD = DC ∴∠BDA =∠DAC ∴ BD∥OA 又∵AB∥DO ∴四边形 AODB 是平行四边形 ∵OA=OD ∴平行四边形 AODB 是菱形 9．（1）①40．②0． （2）不合理．例如，对两个相似而不全等的矩形来说，它们接近正方形的程度是相同 的，但 a b 却不相等．合理定义方法不唯一，如定义为 b a ． b a 越小，矩形越接近于正方 形； b a 越大，矩形与正方形的形状差异越大；当 1b a  时，矩形就变成了正方形． 10．解：∵ ⊙A 分别与两个半圆相切于点 E、F，点 A、B、C 分别是三个圆的圆心， ∴ AE＝AF＝4，BE＝CF＝2，AB＝AC＝6． 则在△AEF 和△ABC 中， ∠EAF＝∠BAC， 4 2 6 3 AE AF AB AC    ． ∴ △AEF∽△ABC ． 故 EF AE BC AB  ．则 EF＝ AEBC AB  ＝ 2 168 3 3   ．