吉林省中考数学试卷和答案 22页

吉林省2017年中考数学真题试卷、答案 ‎　‎ 一、单项选择题（每小题2分，共12分）‎ ‎1．计算（﹣1）2的正确结果是（　　）‎ A．1 B．2 C．﹣1 D．﹣2‎ ‎2．如图是一个正六棱柱的茶叶盒，其俯视图为（　　）‎ A． B．‎ ‎ C． D．‎ ‎3．下列计算正确的是（　　）‎ A．a2+a3=a5 B．a2•a3=a6 C．（a2）3=a6 D．（ab）2=ab2‎ ‎4．不等式x+1≥2的解集在数轴上表示正确的是（　　）‎ A． B． C． D．‎ ‎5．如图，在△ABC中，以点B为圆心，以BA长为半径画弧交边BC于点D，连接AD．若∠B=40°，∠C=36°，则∠DAC的度数是（　　）‎ 第22页（共22页）‎ A．70° B．44° C．34° D．24°‎ ‎6．如图，直线l是⊙O的切线，A为切点，B为直线l上一点，连接OB交⊙O于点C．若AB=12，OA=5，则BC的长为（　　）‎ A．5 B．6 C．7 D．8‎ ‎　‎ 二、填空题（每小题3分，共24分）‎ ‎7．2016年我国资助各类家庭困难学生超过84 000 000人次．将84 000 000这个数用科学记数法表示为　 　．‎ ‎8．苹果原价是每千克x元，按8折优惠出售，该苹果现价是每千克　 　元（用含x的代数式表示）．‎ ‎9．分解因式：a2+4a+4=　 　．‎ ‎10．我们学过用直尺和三角尺画平行线的方法，如图所示，直线a∥b的根据是　 　．‎ 第22页（共22页）‎ ‎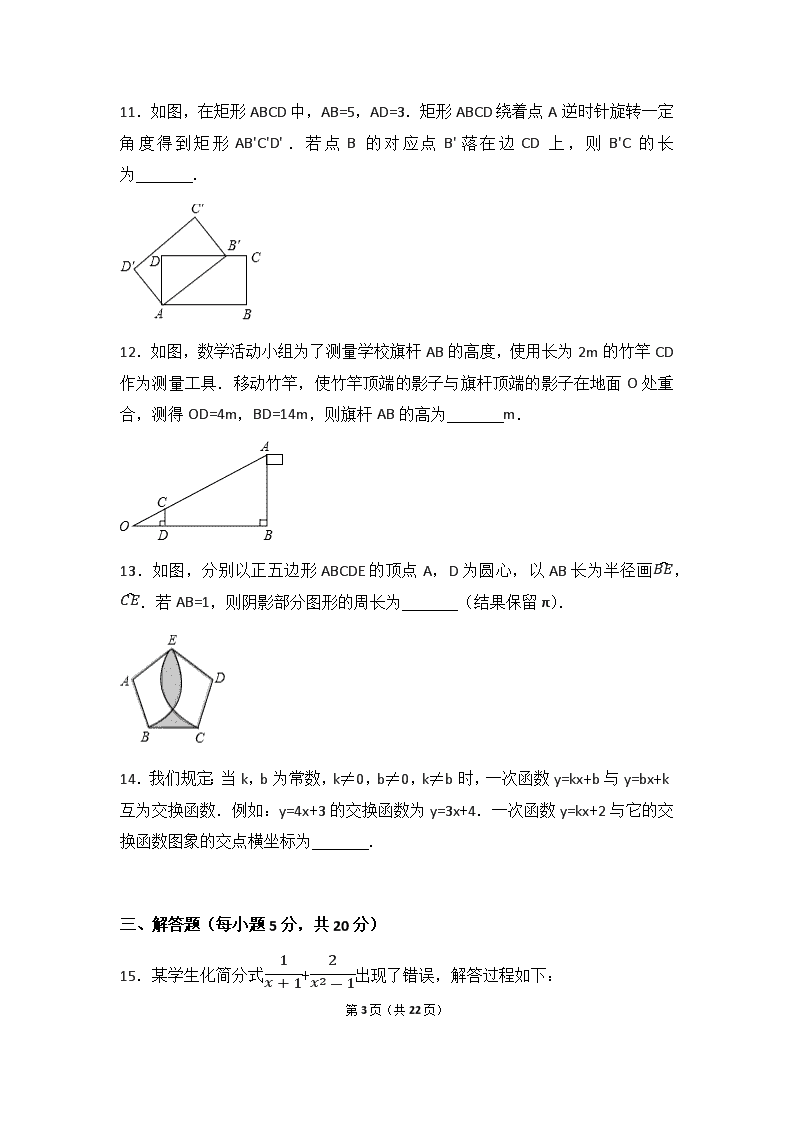11．如图，在矩形ABCD中，AB=5，AD=3．矩形ABCD绕着点A逆时针旋转一定角度得到矩形AB'C'D'．若点B的对应点B'落在边CD上，则B'C的长为　 　．‎ ‎12．如图，数学活动小组为了测量学校旗杆AB的高度，使用长为2m的竹竿CD作为测量工具．移动竹竿，使竹竿顶端的影子与旗杆顶端的影子在地面O处重合，测得OD=4m，BD=14m，则旗杆AB的高为　 　m．‎ ‎13．如图，分别以正五边形ABCDE的顶点A，D为圆心，以AB长为半径画BE，CE．若AB=1，则阴影部分图形的周长为　 　（结果保留π）．‎ ‎14．我们规定：当k，b为常数，k≠0，b≠0，k≠b时，一次函数y=kx+b与y=bx+k互为交换函数．例如：y=4x+3的交换函数为y=3x+4．一次函数y=kx+2与它的交换函数图象的交点横坐标为　 　．‎ ‎　‎ 三、解答题（每小题5分，共20分）‎ 第22页（共22页）‎ ‎15．某学生化简分式‎1‎x+1‎+‎2‎x‎2‎‎-1‎出现了错误，解答过程如下：‎ 原式=‎1‎‎(x+1)(x-1)‎+‎2‎‎(x+1)(x-1)‎（第一步）‎ ‎=‎1+2‎‎(x+1)(x-1)‎（第二步）‎ ‎=‎3‎x‎2‎‎-1‎．（第三步）‎ ‎（1）该学生解答过程是从第　 　步开始出错的，其错误原因是　 　；‎ ‎（2）请写出此题正确的解答过程．‎ ‎16．被誉为“最美高铁”的长春至珲春城际铁路途经许多隧道和桥梁，其中隧道累计长度与桥梁累计长度之和为342km，隧道累计长度的2倍比桥梁累计长度多36km．求隧道累计长度与桥梁累计长度．‎ ‎17．在一个不透明的盒子中装有三张卡片，分别标有数字1，2，3，这些卡片除数字不同外其余均相同．小吉从盒子中随机抽取一张卡片记下数字后放回，洗匀后再随机抽取一张卡片．用画树状图或列表的方法，求两次抽取的卡片上数字之和为奇数的概率．‎ ‎18．如图，点E、F在BC上，BE=FC，AB=DC，∠B=∠C．求证：∠A=∠D．‎ ‎　‎ 四、解答题（每小题7分，共28分）‎ ‎19．某商场甲、乙、丙三名业务员5个月的销售额（单位：万元）如下表：‎ 月份 第1月 第2月 第3月 第4月 第5月 第22页（共22页）‎ 销售额 人员 甲 ‎7.2‎ ‎9.6‎ ‎9.6‎ ‎7.8‎ ‎9.3‎ 乙 ‎5.8‎ ‎9.7‎ ‎9.8‎ ‎5.8‎ ‎9.9‎ 丙 ‎4‎ ‎6.2‎ ‎8.5‎ ‎9.9‎ ‎9.9‎ ‎（1）根据上表中的数据，将下表补充完整：‎ 统计值 数值 人员 平均数（万元）‎ 中位数（万元）‎ 众数（万元）‎ 甲 ‎　 　‎ ‎9.3‎ ‎9.6‎ 乙 ‎8.2‎ ‎　 　‎ ‎5.8‎ 丙 ‎7.7‎ ‎8.5‎ ‎　 　‎ ‎（2）甲、乙、丙三名业务员都说自己的销售业绩好，你赞同谁的说法？请说明理由．‎ ‎20．图①、图②、图③都是由边长为1的小等边三角形构成的网格，每个小等边三角形的顶点称为格点．线段AB的端点在格点上．‎ ‎（1）在图①‎ 第22页（共22页）‎ ‎、图2中，以AB为边各画一个等腰三角形，且第三个顶点在格点上；（所画图形不全等）‎ ‎（2）在图③中，以AB为边画一个平行四边形，且另外两个顶点在格点上．‎ ‎21．如图，一枚运载火箭从距雷达站C处5km的地面O处发射，当火箭到达点A，B时，在雷达站C处测得点A，B的仰角分别为34°，45°，其中点O，A，B在同一条直线上．求A，B两点间的距离（结果精确到0.1km）．‎ ‎（参考数据：sin34°=0.56，cos34°=0.83，tan34°=0.67．）‎ ‎22．如图，在平面直角坐标系中，直线AB与函数y=kx（x＞0）的图象交于点A（m，2），B（2，n）．过点A作AC平行于x轴交y轴于点C，在y轴负半轴上取一点D，使OD=‎1‎‎2‎OC，且△ACD的面积是6，连接BC．‎ ‎（1）求m，k，n的值；‎ ‎（2）求△ABC的面积．‎ ‎　‎ 五、解答题（每小题8分，共16分）‎ ‎23．如图①，BD是矩形ABCD的对角线，∠ABD=30°，AD=1．将△‎ 第22页（共22页）‎ BCD沿射线BD方向平移到△B'C'D'的位置，使B'为BD中点，连接AB'，C'D，AD'，BC'，如图②．‎ ‎（1）求证：四边形AB'C'D是菱形；‎ ‎（2）四边形ABC'D′的周长为　 　；‎ ‎（3）将四边形ABC'D'沿它的两条对角线剪开，用得到的四个三角形拼成与其面积相等的矩形，直接写出所有可能拼成的矩形周长．‎ ‎24．如图①，一个正方体铁块放置在圆柱形水槽内，现以一定的速度往水槽中注水，28s时注满水槽．水槽内水面的高度y（cm）与注水时间x（s）之间的函数图象如图②所示．‎ ‎（1）正方体的棱长为　 　cm；‎ ‎（2）求线段AB对应的函数解析式，并写出自变量x的取值范围；‎ ‎（3）如果将正方体铁块取出，又经过t（s）恰好将此水槽注满，直接写出t的值．‎ ‎　‎ 第22页（共22页）‎ 六、解答题（每小题10分，共20分）‎ ‎25．如图，在Rt△ABC中，∠ACB=90°，∠A=45°，AB=4cm．点P从点A出发，以2cm/s的速度沿边AB向终点B运动．过点P作PQ⊥AB交折线ACB于点Q，D为PQ中点，以DQ为边向右侧作正方形DEFQ．设正方形DEFQ与△ABC重叠部分图形的面积是y（cm2），点P的运动时间为x（s）．‎ ‎（1）当点Q在边AC上时，正方形DEFQ的边长为　 　cm（用含x的代数式表示）；‎ ‎（2）当点P不与点B重合时，求点F落在边BC上时x的值；‎ ‎（3）当0＜x＜2时，求y关于x的函数解析式；‎ ‎（4）直接写出边BC的中点落在正方形DEFQ内部时x的取值范围．‎ ‎26．《函数的图象与性质》拓展学习片段展示：‎ ‎【问题】如图①，在平面直角坐标系中，抛物线y=a（x﹣2）2﹣‎4‎‎3‎经过原点O，与x轴的另一个交点为A，则a=　 　．‎ ‎【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方，将这部分图象与原抛物线剩余部分的图象组成的新图象记为G，如图②．直接写出图象G对应的函数解析式．‎ ‎【探究】在图②中，过点B（0，1）作直线l平行于x轴，与图象G的交点从左至右依次为点C，D，E，F，如图③．求图象G在直线l上方的部分对应的函数y随x增大而增大时x的取值范围．‎ ‎【应用】P是图③中图象G上一点，其横坐标为m，连接PD，PE．直接写出△PDE的面积不小于1时m的取值范围．‎ 第22页（共22页）‎ ‎　‎ 第22页（共22页）‎ 答案 一、单项选择题（每小题2分，共12分）‎ ‎1．A．‎ ‎2．B．‎ ‎3．C ‎　‎ ‎4．A．‎ ‎　‎ ‎5．解：∵AB=BD，∠B=40°，‎ ‎∴∠ADB=70°，‎ ‎∵∠C=36°，‎ ‎∴∠DAC=∠ADB﹣∠C=34°．‎ ‎6．D．‎ 二、填空题（每小题3分，共24分）‎ ‎7．8.4×107．‎ ‎8．0.8x．‎ ‎9．（a+2）2．‎ 第22页（共22页）‎ ‎10．同位角相等，两直线平行．‎ ‎11．解：由旋转的性质得到AB=AB′=5，‎ 在直角△AB′D中，∠D=90°，AD=3，AB′=AB=5，‎ 所以B′D=AB‎'‎‎2‎-AD‎2‎=‎5‎‎2‎‎-‎‎3‎‎2‎=4，‎ 所以B′C=5﹣B′D=1．‎ 故答案是：1．‎ ‎12．解：‎ ‎∵OD=4m，BD=14m，‎ ‎∴OB=OD+BD=18m，‎ 由题意可知∠ODC=∠OBA，且∠O为公共角，‎ ‎∴△OCD∽△OAB，‎ ‎∴ODOB=CDAB，即‎4‎‎18‎=‎2‎AB，解得AB=9，‎ 即旗杆AB的高为9m．‎ ‎13．解：∵五边形ABCDE为正五边形，AB=1，‎ ‎∴AB=BC=CD=DE=EA=1，∠A=∠D=108°，‎ ‎∴BE=CE=‎108°‎‎180°‎•πAB=‎3‎‎5‎π，‎ 第22页（共22页）‎ ‎∴C阴影=BE+CE+BC=‎6‎‎5‎π+1．‎ ‎14．1．‎ 三、解答题（每小题5分，共20分）‎ ‎15．解：（1）一、分式的基本性质用错；‎ ‎（2）原式=x-1‎‎(x+1)(x-1)‎+‎‎2‎‎(x+1)(x-1)‎ ‎=‎x+1‎‎(x+1)(x-1)‎ ‎=‎‎1‎x-1‎ ‎16．解：设隧道累计长度为xkm，桥梁累计长度为yk，‎ 根据题意得：‎&x+y=342‎‎&2x=y+36‎，‎ 解得：‎&x=126‎‎&y=216‎．‎ 答：隧道累计长度为126km，桥梁累计长度为216km．‎ ‎17．解：画树状图得：‎ ‎∵共有9种等可能的结果，两次抽取的卡片上数字之和是奇数的有4种情况，‎ ‎∴两次两次抽取的卡片上数字之和是奇数的概率为‎4‎‎9‎．‎ ‎18．证明：∵BE=FC，‎ ‎∴BE+EF=CF+EF，‎ 即BF=CE；‎ 第22页（共22页）‎ 又∵AB=DC，∠B=∠C，‎ ‎∴△ABF≌△DCE；（SAS）‎ ‎∴∠A=∠D．‎ 四、解答题（每小题7分，共28分）‎ ‎19．解：（1）x甲=‎1‎‎5‎（7.2+9.6+9.6+7.8+9.3）=8.7（万元）‎ 把乙按照从小到大依次排列，可得5.8，5.8，9.7，9.8，9.9；‎ 中位数为9.7万元．‎ 丙中出现次数最多的数为9.9万元．‎ 故答案为：8.7，9.7，9.9；‎ ‎（2）我赞同甲的说法．甲的平均销售额比乙、丙都高．‎ ‎20．解：（1）如图①、②所示，△ABC和△ABD即为所求；‎ ‎（2）如图③所示，▱ABCD即为所求．‎ ‎21．解：由题意可得：∠AOC=90°，OC=5km．‎ 在Rt△AOC中，‎ ‎∵tan34°=OAOC，‎ 第22页（共22页）‎ ‎∴OA=OC•tan34°=5×0.67=3.35km，‎ 在Rt△BOC中，∠BCO=45°，‎ ‎∴OB=OC=5km，‎ ‎∴AB=5﹣3.35=1.65≈1.7km，‎ 答：求A，B两点间的距离约为1.7km．‎ ‎22．解：（1）∵点A的坐标为（m，2），AC平行于x轴，‎ ‎∴OC=2，AC⊥y轴，‎ ‎∵OD=‎1‎‎2‎OC，‎ ‎∴OD=1，‎ ‎∴CD=3，‎ ‎∵△ACD的面积为6，‎ ‎∴‎1‎‎2‎CD•AC=6，‎ ‎∴AC=4，即m=4，‎ 则点A的坐标为（4，2），将其代入y=kx可得k=8，‎ ‎∵点B（2，n）在y=‎8‎x的图象上，‎ ‎∴n=4；‎ ‎（2）如图，过点B作BE⊥AC于点E，则BE=2，‎ 第22页（共22页）‎ ‎∴S△ABC=‎1‎‎2‎AC•BE=‎1‎‎2‎×4×2=4，‎ 即△ABC的面积为4．‎ 五、解答题（每小题8分，共16分）‎ ‎23．解：（1）∵BD是矩形ABCD的对角线，∠ABD=30°，‎ ‎∴∠ADB=60°，‎ 由平移可得，B'C'=BC=AD，∠D'B'C'=∠DBC=∠ADB=60°，‎ ‎∴AD∥B'C'‎ ‎∴四边形AB'C'D是平行四边形，‎ ‎∵B'为BD中点，‎ ‎∴Rt△ABD中，AB'=‎1‎‎2‎BD=DB'，‎ 又∵∠ADB=60°，‎ ‎∴△ADB'是等边三角形，‎ ‎∴AD=AB'，‎ ‎∴四边形AB'C'D是菱形；‎ ‎（2）由平移可得，AB=C'D'，∠ABD'=∠C'D'B=30°，‎ 第22页（共22页）‎ ‎∴AB∥C'D'，‎ ‎∴四边形ABC'D'是平行四边形，‎ 由（1）可得，AC'⊥B'D，‎ ‎∴四边形ABC'D'是菱形，‎ ‎∵AB=‎3‎AD=‎3‎，‎ ‎∴四边形ABC'D′的周长为4‎3‎，‎ ‎（3）将四边形ABC'D'沿它的两条对角线剪开，用得到的四个三角形拼成与其面积相等的矩形如下：‎ ‎∴矩形周长为6+‎3‎或2‎3‎+3．‎ ‎　‎ ‎24．解：（1）由题意可得：12秒时，水槽内水面的高度为10cm，12秒后水槽内高度变化趋势改变，‎ 故正方体的棱长为10cm；‎ ‎（2）设线段AB对应的函数解析式为：y=kx+b，‎ ‎∵图象过A（12，0），B（28，20），‎ ‎∴‎&12k+b=10‎‎&28k+b=20‎，‎ 第22页（共22页）‎ 解得：‎&k=‎‎5‎‎8‎‎&b=‎‎5‎‎2‎，‎ ‎∴线段AB对应的解析式为：y=‎5‎‎8‎x+‎5‎‎2‎（12≤x≤28）；‎ ‎（3）∵28﹣12=16（cm），‎ ‎∴没有立方体时，水面上升10cm，所用时间为：16秒，‎ ‎∵前12秒由立方体的存在，导致水面上升速度加快了4秒，‎ ‎∴将正方体铁块取出，经过4秒恰好将此水槽注满．‎ 六、解答题（每小题10分，共20分）‎ ‎25．解：（1）∵∠ACB=90°，∠A=45°，PQ⊥AB，‎ ‎∴∠AQP=45°，‎ ‎∴PQ=AP=2x，‎ ‎∵D为PQ中点，‎ ‎∴DQ=x，‎ 故答案为：x；‎ ‎（2）如图①，延长FE交AB于G，由题意得AP=2x，‎ ‎∵D为PQ中点，‎ ‎∴DQ=x，‎ ‎∴GP=2x，‎ ‎∴2x+x+2x=4，‎ 第22页（共22页）‎ ‎∴x=‎4‎‎5‎；‎ ‎（3）如图②，当0＜x≤‎4‎‎5‎时，y=S正方形DEFQ=DQ2=x2，‎ ‎∴y=x2；‎ 如图③，当‎4‎‎5‎＜x≤1时，过C作CH⊥AB于H，交FQ于K，则CH=‎1‎‎2‎AB=2，‎ ‎∵PQ=AP=2x，CK=2﹣2x，‎ ‎∴MQ=2CK=4﹣4x，FM=x﹣（4﹣4x）=5x﹣4，‎ ‎∴y=S正方形DEFQ﹣S△MNF=DQ2﹣‎1‎‎2‎FM2，‎ ‎∴y=x2﹣‎1‎‎2‎（5x﹣4）2=﹣‎23‎‎2‎x2+20x﹣8，‎ ‎∴y=﹣‎23‎‎2‎x2+20x﹣8；‎ 如图④，当1＜x＜2时，PQ=4﹣2x，‎ ‎∴DQ=2﹣x，‎ ‎∴y=S△DEQ=‎1‎‎2‎DQ2，‎ ‎∴y=‎1‎‎2‎（2﹣x）2，‎ ‎∴y=‎1‎‎2‎x2﹣2x+2；‎ ‎（4）当Q与C重合时，E为BC的中点，‎ 即2x=2，‎ ‎∴x=1，‎ 当Q为BC的中点时，BQ=‎2‎，‎ 第22页（共22页）‎ PB=1，‎ ‎∴AP=3，‎ ‎∴2x=3，‎ ‎∴x=‎3‎‎2‎，‎ ‎∴边BC的中点落在正方形DEFQ内部时x的取值范围为：1＜x＜‎3‎‎2‎．‎ ‎　‎ ‎26．解：【问题】‎ ‎∵抛物线y=a（x﹣2）2﹣‎4‎‎3‎经过原点O，‎ 第22页（共22页）‎ ‎∴0=a（0﹣2）2﹣‎4‎‎3‎，‎ a=‎1‎‎3‎，‎ 故答案为：‎1‎‎3‎；‎ ‎【操作】：如图①，抛物线：y=‎1‎‎3‎（x﹣2）2﹣‎4‎‎3‎，‎ 对称轴是：直线x=2，由对称性得：A（4，0），‎ 沿x轴折叠后所得抛物线为：y=﹣‎1‎‎3‎（x﹣2）2+‎‎4‎‎3‎ 如图②，图象G对应的函数解析式为：y=‎&‎1‎‎3‎(x-2‎)‎‎2‎-‎4‎‎3‎(x≤0或x≥4)‎‎&-‎1‎‎3‎(x-2‎)‎‎2‎+‎4‎‎3‎(0＜x＜4)‎；‎ ‎【探究】：如图③，由题意得：‎ 当y=1时，‎1‎‎3‎（x﹣2）2﹣‎4‎‎3‎=0，‎ 解得：x1=2+‎7‎，x2=2﹣‎7‎，‎ ‎∴C（2﹣‎7‎，1），F（2+‎7‎，1），‎ 当y=1时，﹣‎1‎‎3‎（x﹣2）2+‎4‎‎3‎=0，‎ 解得：x1=3，x2=1，‎ ‎∴D（1，1），E（3，1），‎ 由图象得：图象G在直线l上方的部分，当1＜x＜2或x＞2+‎7‎时，函数y随x增大而增大；‎ 第22页（共22页）‎ ‎【应用】：∵D（1，1），E（3，1），‎ ‎∴DE=3﹣1=2，‎ ‎∵S△PDE=‎1‎‎2‎DE•h≥1，‎ ‎∴h≥1；‎ ‎①当P在C的左侧或F的右侧部分时，设P[m，‎1‎‎3‎‎(m-2‎)‎‎2‎-‎‎4‎‎3‎]，‎ ‎∴h=‎1‎‎3‎（m﹣2）2﹣‎4‎‎3‎﹣1≥1，‎ ‎（m﹣2）2≥10，‎ m﹣2≥‎10‎或m﹣2≤﹣‎10‎，‎ m≥2+‎10‎或m≤2﹣‎10‎，‎ ‎②如图③，作对称轴交抛物线G于H，交直线CD于M，交x轴于N，‎ ‎∵H（2，‎4‎‎3‎），‎ ‎∴HM=‎4‎‎3‎﹣1=‎1‎‎3‎＜1，‎ ‎∴当点P不可能在DE的上方；‎ ‎③∵MN=1，‎ 且O（0，0），a（4，0），‎ ‎∴P与O或A重合时，符合条件，‎ ‎∴m=0或m=4；‎ 综上所述，△PDE的面积不小于1时，m的取值范围是：m=0或m=4或m≤2﹣‎ 第22页（共22页）‎ ‎10‎或m≥2+‎10‎．‎ 第22页（共22页）‎