中考数学总复习训练分类讨论型问题 16页

‎ 分类讨论型问题 一、选择题 ‎1．如果x2＋mx＋9是一个完全平方式，那么m的值为(C)‎ A．±3 B．±9‎ C．±6 D．6‎ ‎【解析】　完全平方式是(x±3)2，故m＝±6.‎ ‎2．已知函数y＝(k－3)x2＋2x＋1的图象与x轴有交点，则k的取值范围是(B)‎ A．k＜4 B．k≤4‎ C．k＜4且k≠3 D．k≤4且k≠3‎ ‎【解析】　①当k－3≠0时，(k－3)x2＋2x＋1＝0，‎ Δ＝b2－‎4ac＝22－4(k－3)×1＝－4k＋16≥0，k≤4；‎ ‎②当k－3＝0，即k＝3时，y＝2x＋1，与x轴有交点．‎ 故选B.‎ ‎3．若正比例函数y＝2kx与反比例函数y＝(k≠0)的图象交于点A(m，1)，则k的值是(B)‎ A．－或 B．－或 C. D. ‎【解析】　把A(m，1)代入y＝中，得m＝k.‎ 把A(m，1)代入y＝2kx中，得‎2km＝1，即2k2＝1，‎ ‎∴k2＝，∴k＝±.‎ ‎4．⊙O的直径为‎10 cm，弦AB为‎8 cm，P是弦AB上一点，若OP的长为整数，则满足条件的点P有(D)‎ A．2个 B．3个 C．4个 D．5个 ‎【解析】　OP为3时有一条，为4时有两条，为5时有两条，共5条．‎ ‎(第5题)‎ ‎5．如图，已知点A(－1，0)和点B(1，2)，在坐标轴上确定点P，使得△ABP为直角三角形，那么满足这样条件的点P共有(C)‎ A．2个　　　　　　B．4个 C．6个　　　　　　D．7个 ‎【解析】　当以AB为斜边时，∠APB＝90°，与坐标轴有3个交点；当∠PAB＝90°时，与y轴有一个交点；当∠PBA＝90°时，与x轴，y轴各有1个交点．∴点P共有6个．‎ ‎6．如图，已知直线l的表达式是y＝x－4，并且与x轴，y轴分别交于A，B两点．一个半径为1.5的⊙C，圆心C从点(0，1.5)开始以每秒0.5个单位的速度沿着y轴向下运动，当⊙C与直线l相切时，则该圆的运动时间为(D)‎ A．3 s或6 s B．6 s C．3 s D．6 s或16 s ‎(第6题)‎ ‎　　(第6题解)‎ ‎【解析】　如解图．‎ ‎∵当x＝0时，y＝－4；当y＝0时，x＝3，‎ ‎∴点A(3，0)，B(0，－4)，∴AB＝5.‎ 当点C在点B上方，直线与圆相切时，连结CD，‎ 则点C到AB的距离等于1.5，‎ ‎∴CB＝1.5÷sin∠ABC＝1.5×＝2.5.‎ ‎∴点C运动的距离为1.5＋(4－2.5)＝3，运动的时间为3÷0.5＝6(s)．‎ 同理，当点C在点B下方，直线与圆相切时，‎ 连结CD，则点C运动的距离为1.5＋(4＋2.5)＝8，运动的时间为8÷0.5＝16(s)．‎ 故选D.‎ ‎(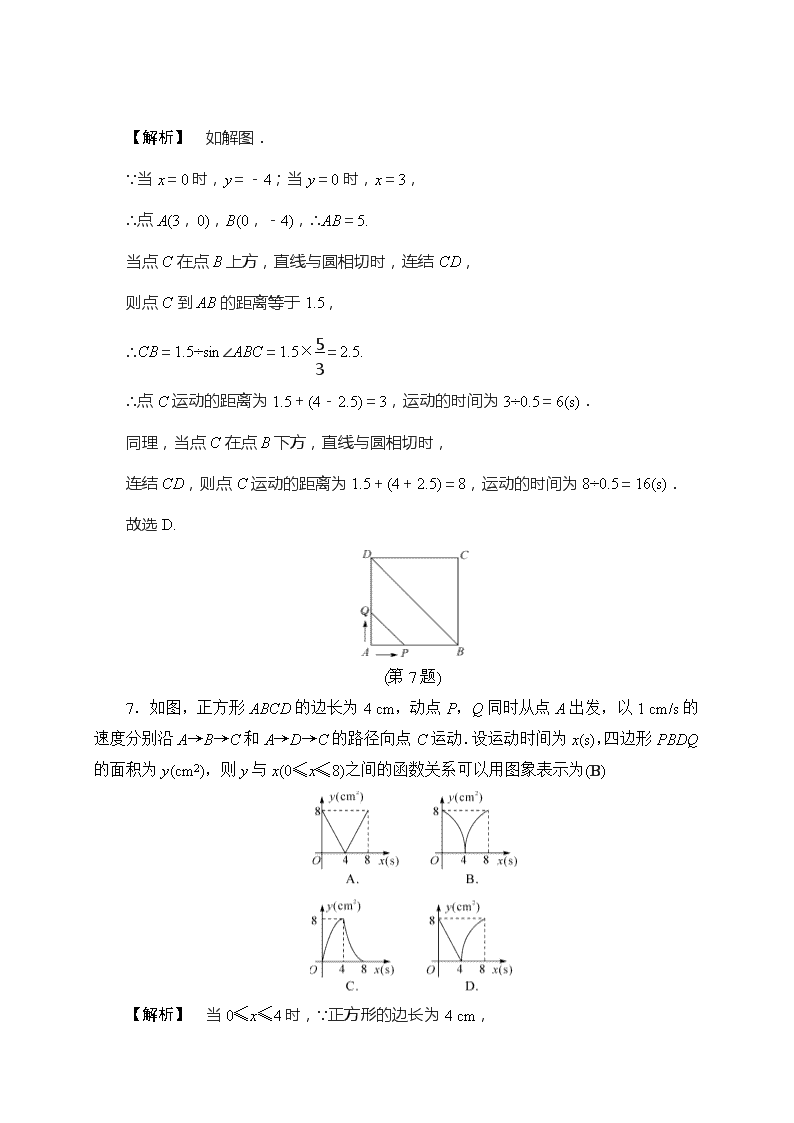第7题)‎ ‎7．如图，正方形ABCD的边长为‎4 cm，动点P，Q同时从点A出发，以‎1 cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动．设运动时间为x(s)，四边形PBDQ的面积为y(cm2)，则y与x(0≤x≤8)之间的函数关系可以用图象表示为(B)‎ ‎【解析】　当0≤x≤4时，∵正方形的边长为‎4 cm，‎ ‎∴y＝S△ABD－S△APQ＝×4×4－·x·x＝8－x2；‎ 当40)，过点B作BF垂直y轴于点F，同上可得BF2＝AF·FM，‎ ‎(第20题解⑤)‎ ‎∴＝，‎ 解得q＝.‎ 此时，点M.‎ 综上所述，除点C外，在坐标轴上还存在点M，使得△MAB是直角三角形，满足条件的点M的坐标是或或或或，共五个点．‎