上海中考数学初三相似三角形判定与性质 7页

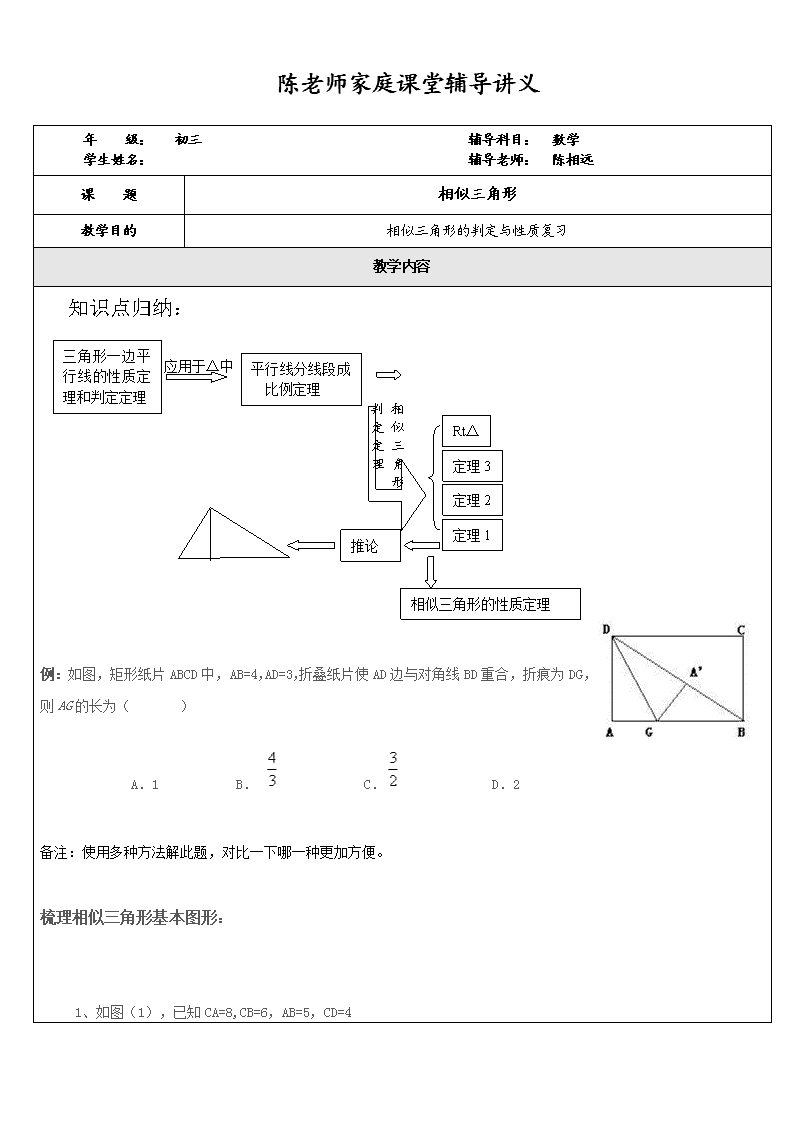
‎ 陈老师家庭课堂辅导讲义 年 级： 初三 辅导科目： 数学 ‎ 学生姓名： 辅导老师： 陈相远 课 题 相似三角形 教学目的 相似三角形的判定与性质复习 教学内容 知识点归纳：‎ 三角形一边平行线的性质定理和判定定理 ‎（‎ 应用于△中 定理1‎ 定理2‎ 定理3‎ Rt△‎ 平行线分线段成比例定理 ‎ ‎ 相似三角形 判定定理 推论 相似三角形的性质定理 例：如图，矩形纸片ABCD中，AB=4，AD=3，折叠纸片使AD边与对角线BD重合，折痕为DG，则AG的长为（    ）‎ ‎       A．1      B．       C．       D．2‎ 备注：使用多种方法解此题，对比一下哪一种更加方便。‎ 梳理相似三角形基本图形：‎ ‎1、如图（1），已知CA=8,CB=6，AB=5，‎ CD=4 (1)若CE= 3，则DE=____ (2) 如图（2）若CE=  ，则DE=____. ‎ ‎2、如图（3），在⊿ABC中，D为AC边上一点，∠DBC= ∠A，BC=  ，AC=3，则CD的长为（     ）‎ ‎（A）1      （B）2      （C）       （D）    ‎ ‎3、如图（4），∠ABC=90埃?SPAN>BD⊥AC于D，DC=4 ，AD=9，则BD的长为（     ）‎ ‎（A）36     （B）16       （C） 6      （D）     ‎ ‎4、如图，F、C、D共线，BD⊥FD, EF⊥FD ， BC⊥EC ,若DC=2 ，BD=3，FC=9,则EF的长为（     ）‎ ‎（A）6     （B）16     （C） 26   （D）‎ 归纳小结相似三角形的基本图形：‎ ‎ “A”型    公共角型     公共边角型    双垂直型   三垂直型 ‎ ‎ ‎ ‎ ‎ ‎ ‎“X”型         蝴蝶型 旋转型 ‎ ‎ 课堂练习学生探究：‎ ‎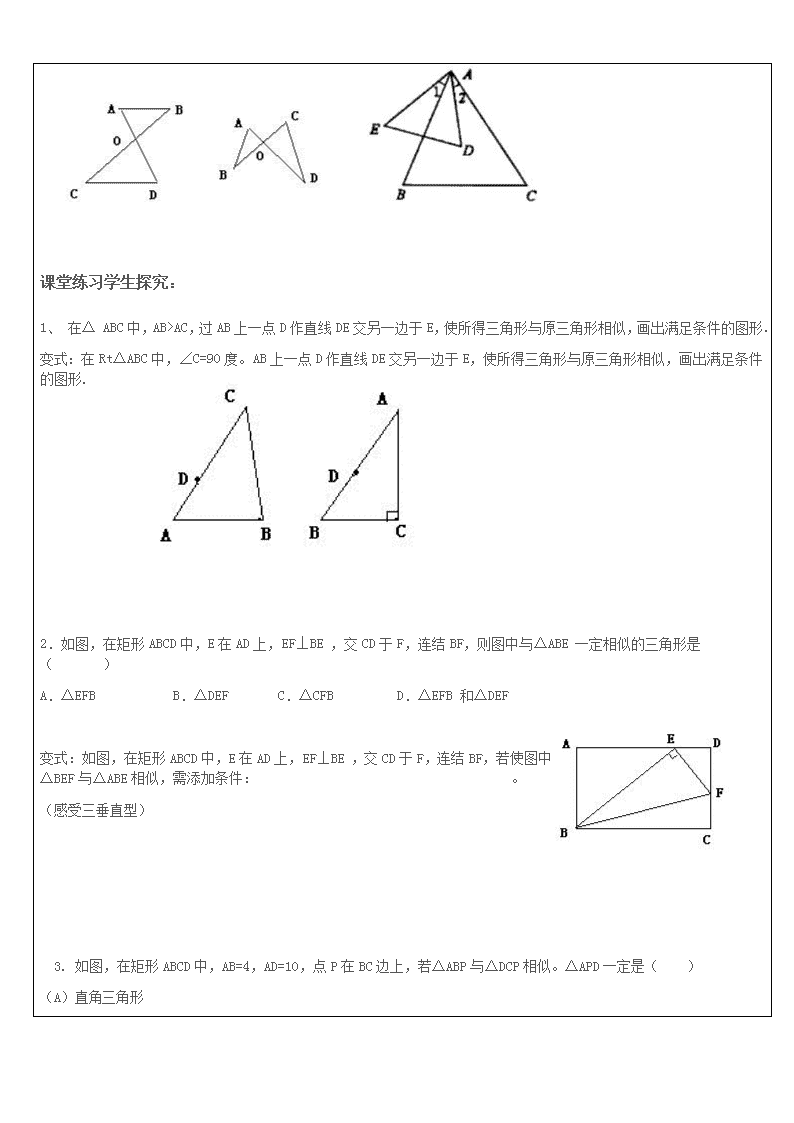1、 在△ ABC中，AB>AC，过AB上一点D作直线DE交另一边于E，使所得三角形与原三角形相似，画出满足条件的图形.‎ 变式：在Rt△ABC中，∠C=90度。AB上一点D作直线DE交另一边于E，使所得三角形与原三角形相似，画出满足条件的图形.‎ ‎ ‎ ‎ ‎ ‎2．如图，在矩形ABCD中，E在AD上，EF⊥BE ，交CD于F，连结BF，则图中与△ABE 一定相似的三角形是（    ）‎ A．△EFB      B．△DEF    C．△CFB     D．△EFB 和△DEF 变式：如图，在矩形ABCD中，E在AD上，EF⊥BE ，交CD于F，连结BF，若使图中△BEF与△ABE相似，需添加条件：                   。‎ ‎（感受三垂直型）‎ ‎ 3. 如图，在矩形ABCD中，AB=4，AD=10，点P在BC边上，若△ABP与△DCP相似。△APD一定是（　　）‎ ‎（A）直角三角形 ‎  （B）等腰三角形 ‎  （C）等腰直角三角形　‎ ‎  （D）等腰三角形或直角三角形 变式： 如图，在矩形ABCD中，AB=4，AD=10，若点P在BC边上，则△ABP与△DCP相似的点P有        个。‎ 课堂练习：‎ ‎1.如图，在△ABC中，AB＝AC，AD是中线，P是AD上一点，过点C作CF∥AB，延长BP交AC于点E，交CF于点F，证明：BP2＝PE·PF。‎ A B C D F P ‎ ‎ ‎2.已知：如图，在直角三角形ABC中，∠BAC= 90°，AB= AC，D为BC的中点，E为AC上一点，‎ 点G在BE上，连结DG并延长交AE于F，若∠FGE= 45°，‎ ‎（1）求证：BD·BC= BG·BE；‎ ‎（2）求证：AG⊥BE；‎ ‎（3）若E为AC的中点，求EF∶FD的值。‎ ‎ ‎ ‎3.已知∠AOB=90°，OM是∠AOB的平分线，按以下要求解答问题：‎ ‎(1)将三角板的直角顶点P在射线OM上移动，两直角边分别与边OA，OB交于点C，D。‎ ‎①在图甲中，证明：PC=PD。‎ ‎②在图乙中，点G是CD与OP的交点，且PG=PD，求△POD与△PDG的面积之比。‎ ‎（2）将三角板的直角顶点P在射线OM上移动，一直角边与边OB交于点D，OD=1，‎ 另一直角边与直线OA，直线OB分别交于点C，E，使以P，D，E为顶点的三角形与△OCD相似，‎ 在图丙中作出图形，试求OP的长。‎ A B O M 图丙 A B C O P M D 图乙_‎ 图甲 D M P E O C B G 课后作业：‎ 一、填空题 ‎1、在等边三角形ABC中，点D、E分别在AB、AC上，且DE∥BC。‎ 如果BC = ‎8cm，AD:AB = 1:4，那么ΔADE的周长为 cm 。(如图1)‎ ‎2、已知：如图2，∠ACP =∠B，AC = 4，AP = 2，则AB = 。‎ 二、选择题 ‎1、要做甲、乙两个形状相同( 相似 )的三角形框架，已知三角形框架甲的三边分 别为‎50cm、‎60cm、‎80cm，三角形框架乙的一边长为‎20cm，那么，符合条件的三角形框架乙共有 。‎ ‎ A.1种 B.2种 C.3种 D.4种 ‎2、ΔABC的三条边分别为 ‎54cm、‎45cm、‎63cm，另一个和它相似的三角形最短边长为‎15cm，则这个三角形的最长边为 。‎ ‎ A‎.18cm B‎.24cm C.‎19.8 cm D‎.21cm ‎3、在如图3的ΔABC中,DE∥BC, 且 AD= BD，DE = ‎4cm，则BC = 。‎ ‎ A‎.14cm B‎.12cm C‎.10 cm D‎.8cm 三、解答题 ‎1、如图，梯形ABCD中，AB∥CD，且AB=2CD，E，F分别是AB，BC的中点，‎ EF与BD相交于点M。‎ ‎ （1）求证：△EDM∽△FBM；‎ ‎（2）若DB=9，求BM。‎ ‎2、如图，等边⊿ABC，点D、E分别在BC、AC上，且BD=CE，AD与BE相交于点F。‎ ‎（1）试说明⊿ABD≌⊿BCE。 ‎ ‎（2）⊿AEF与⊿ABE相似吗?说说你的理由。‎ ‎（3）BD2=AD·DF吗？请说明理由。 ‎ ‎ ‎ ‎3、如图所示，在ΔABC中，BA=BC=‎20cm，AC=‎30cm，点P从A点出发，‎ 沿AB以每秒‎4cm的速度向B点运动；同时点Q从C点出发，沿CA以每秒‎3cm的速度向A点运动。‎ 设运动时间为x。‎ ‎（1）当x为何值时，PQ∥BC？‎ ‎（2）当，求的值；‎ ‎（3）ΔAPQ能否与ΔCQB相似？若能，求出AP的长；若不能，请说明理由。‎