2020中考数学复习压轴题动点问题专题提升练习28六大动点必考相关问题29无答案 9页

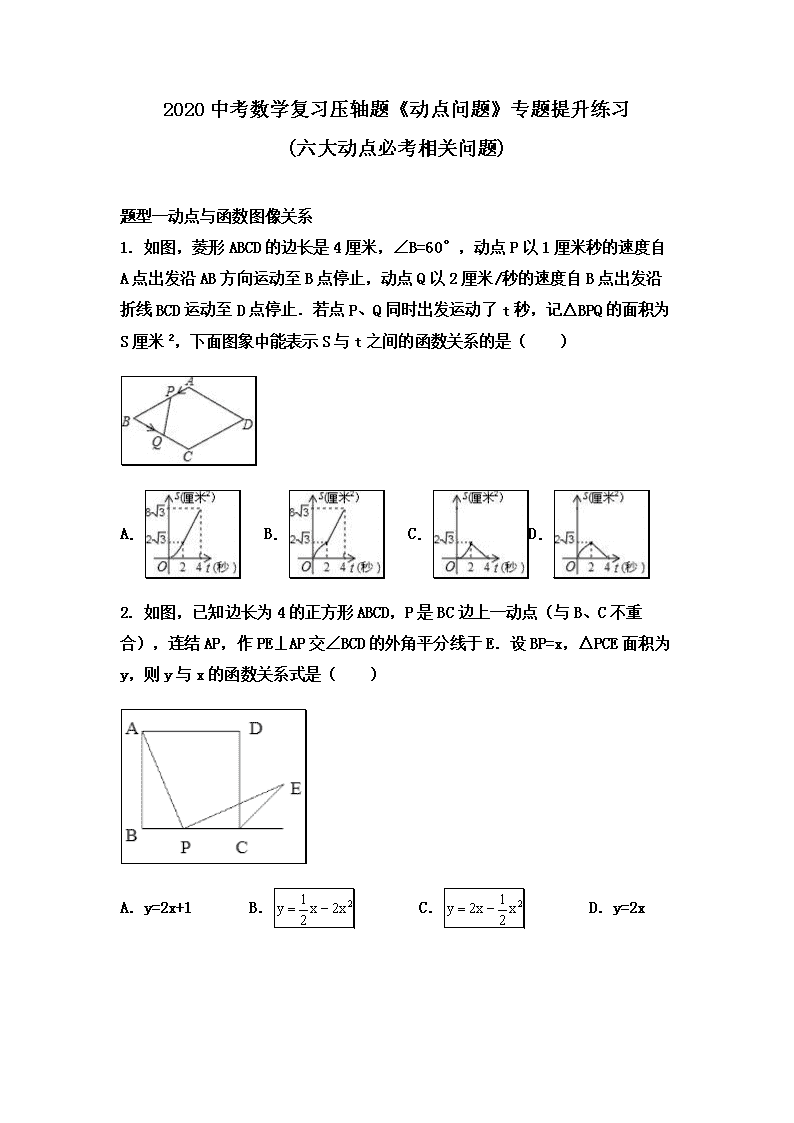
2020中考数学复习压轴题《动点问题》专题提升练习(六大动点必考相关问题)题型一动点与函数图像关系1.如图，菱形ABCD的边长是4厘米，∠B=60°，动点P以1厘米秒的速度自A点出发沿AB方向运动至B点停止，动点Q以2厘米/秒的速度自B点出发沿折线BCD运动至D点停止．若点P、Q同时出发运动了t秒，记△BPQ的面积为S厘米2，下面图象中能表示S与t之间的函数关系的是（　　）A．B．C．D．2.如图，已知边长为4的正方形ABCD，P是BC边上一动点（与B、C不重合），连结AP，作PE⊥AP交∠BCD的外角平分线于E．设BP=x，△PCE面积为y，则y与x的函数关系式是（　　）A．y=2x+1B．C．D．y=2x 3.如图，已知A、B是反比例函数y＝(k＞0，x＞0)图象上的两点，BC∥x轴，交y轴于点C．动点P从坐标原点O出发，沿O→A→B→C匀速运动，终点为C．过点P作PM⊥x轴，PN⊥y轴，垂足分别为M、N．设四边形OMPN的面积为S，点P运动的时间为t，则S关于t的函数图象大致为（ ）.题型二动点与图形面积问题1.如图，在△ABC中，∠C=90°，M是AB的中点，动点P从点A出发，沿AC方向匀速运动到终点C,动点Q从点C出发，沿CB方向匀速运动到终点B.已知P，Q两点同时出发，并同时到达终点.连结MP，MQ，PQ.在整个运动过程中，△MPQ的面积大小变化情况是()A.一直增大B.一直减小C.先减小后增大D.先增大后减小2.如图1，在矩形ABCD中，动点E从点B出发，沿BADC方向运动至点C处停止，设点E运动的路程为x，△BCE的面积为y，如果y关于x的函数图象如图2所示，则当x=7时，点E应运动到() A．点C处B．点D处C．点B处D．点A处3.已知Rt△OAB，∠OAB=90°，∠ABO=30°，斜边OB=4，将Rt△OAB绕点O顺时针旋转60°，如题图1，连接BC.（1）填空：∠OBC=_______°；（2）如图1，连接AC，作OP⊥AC，垂足为P，求OP的长度；（3）如图2，点M，N同时从点O出发，在△OCB边上运动，M沿O→C→B路径匀速运动，N沿O→B→C路径匀速运动，当两点相遇时运动停止，已知点M的运动速度为1.5单位/秒，点N的运动速度为1单位/秒，设运动时间为x秒，△OMN的面积为y，求当x为何值时y取得最大值？最大值为多少？题型三动点与等腰三角形问题1.如图1，在△ABC中，∠ACB＝90°，AC＝4cm，BC＝3cm．如果点P由点B出发沿BA方向向点A匀速运动，同时点Q由点A出发沿AC方向向点C 匀速运动，它们的速度均为1cm/s．连结PQ，设运动时间为t（s）（0＜t＜4），解答下列问题：（1）设△APQ的面积为S，当t为何值时，S取得最大值？S的最大值是多少？（2）如图2，连结PC，将△PQC沿QC翻折，得到四边形PQP′C，当四边形PQP′C为菱形时，求t的值；（3）当t为何值时，△APQ是等腰三角形？图1图22.如图，已知抛物线y=ax2-2ax+b与x轴交于A、B(3, 0)两点，与y轴交于点C，且OC=3OA，设抛物线的顶点为D．(1)求抛物线的解析式(2)在抛物线对称轴的右侧的抛物线上是否存在点P，使得△PDC是等腰三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由；  3.已知：如图，抛物线y=ax2+bx+c经过A(1, 0)、B(5, 0)、C(0, 5)三点．(1)求抛物线的函数关系式；(2)若过点C的直线y=kx+b与抛物线相交于点E (4, m)，请求出△CBE的面积S的值；(3)写出二次函数值大于一次函数值的x的取值范围；(4)在抛物线上是否存在点P使得△ABP为等腰三角形？若存在，请指出一共有几个满足条件的点P，并求出其中一个点的坐标；若不存在这样的点P，请说明理由． 题型四动点与线段最值问题 1.点P为抛物线上直线AM下方一动点，E为线段AM上一动点，且PE//Y轴，当点P的坐标为多少时，线段PE的长度有最大值？2.如图1,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.(1)当AN平分∠MAB时,求DM的长;(2)连结BN,当DM=1时,求△ABN的面积;(3)当射线BN交线段CD于点F时,求DF的最大值.图1备用图3.如图,顶点为A(3,1)的抛物线经过坐标原点O,与x轴交于点B.(1)求抛物线对应的二次函数的表达式;(2)过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB; (3)在x轴上找一点P,使得△PCD的周长最小,求出点P的坐标.题型五动点与切线问题1.如图1,抛物线y=-14x2+mx+n的图象经过点A(2,3),对称轴为直线x=1,一次函数y=kx+b的图象经过点A,交x轴于点P,交抛物线于另一点B,点A、B位于点P的同侧.(1)求抛物线的解析式;(2)若PA∶PB=3∶1,求一次函数的解析式;(3)在(2)的条件下,当k>0时,抛物线的对称轴上是否存在点C,使得☉C同时与x轴和直线AP相切,如果存在,请求出点C的坐标,如果不存在,请说明理由. 2.如图1,在Rt△ABC中,∠ACB=90°,cosB=35,BC=3,P是射线AB上的一个动点,以P为圆心、PA为半径的☉P与射线AC的另一个交点为D,直线PD交直线BC于点E.(1)当PA=1时,求CE的长;(2)如果点P在边AB上,当☉P与以C为圆心、CE为半径的☉C内切时,求☉P的半径;(3)设线段BE的中点为Q,射线PQ与☉P相交于点F,点P在运动过程中,当PE∥CF时,求AP的长.题型六动点与辅助圆问题1.如图，B是线段AC的中点，过点C的直线l与AC成50°的角，在直线l上取一点P，使得∠APB＝30°，则满足条件的点P的个数是（）A．1个B．2个C．3个D．无数个 2.如图，矩形CDEF是由矩形ABCG（AB＜BC）绕点C顺时针旋转90°而得，∠APE的顶点在线段BD上移动，则能够使∠APE为直角的点P的个数是_______．3.如图，已知足球球门宽AB约为5米，一球员从距B点5的C点（点A、B、C均在球场底线上），沿与AC成45°角的CD方向带球．试问，该球员能否在射线CD上找到一点P，使得点P为最佳射门点（即∠APB最大）？若能找到，求出这时点P与点C的距离；若找不到，请说明理由．