中考专题复习讲 　数形结合思想 6页

第3讲　数形结合思想 ‎1．(2012年四川自贡)伟伟从学校匀速回家，刚到家发现当晚要完成的试卷忘记在学校，于是马上以更快的速度匀速沿原路返回学校．在这一情景中，速度v和时间t的函数图象(不考虑图象端点情况)大致是(　　)‎ ‎ ‎ ‎ 　 　　 　 　　 　 　　 ‎2．文具店、书店和玩具店依次坐落在一条东西走向的大街上，文具店在书店西边‎20米处，玩具店位于书店东边‎100米处，小明从书店沿街向东走了‎40米，接着又向东走了－‎60米，此时小明的位置在(　　)‎ A．玩具店 B．文具店 C．文具店西边‎40米 D．玩具店东边－‎‎60米 ‎3．已知实数a，b在数轴上的对应点依次在原点的右边和左边，那么(　　)‎ A．abb C．a＋b>0 D．a－b>0‎ ‎4．已知函数y＝x和y＝的图象如图Z3－3，则不等式>x的解集为(　　)‎ A．－2≤x<2 B．－2≤x≤‎2 C．x<2 D．x>2‎ ‎ ‎ 图Z3－3 图Z3－4 图Z3－5‎ ‎5．如图Z3－4，直线l1∥l2，⊙O与直线l1和直线l2分别相切于点A和点B.点M和点N分别是直线l1和直线l2上的动点，MN沿l1和l2平移．⊙O的半径为1，∠1＝60°.下列结论错误的是(　　)‎ A．MN＝ B．若MN与⊙O相切，则AM＝ C．若∠MON＝90°，则MN与⊙O相切 D．直线l1和直线l2的距离为2‎ ‎6．如图Z3－5，已知四边形OABC为正方形，边长为6，点A、C分别在x轴、y轴的正半轴上，点D在OA上，且点D的坐标为(2,0)，点P是OB上的一个动点，则PD＋PA的最小值是(　　)‎ A．2 B. 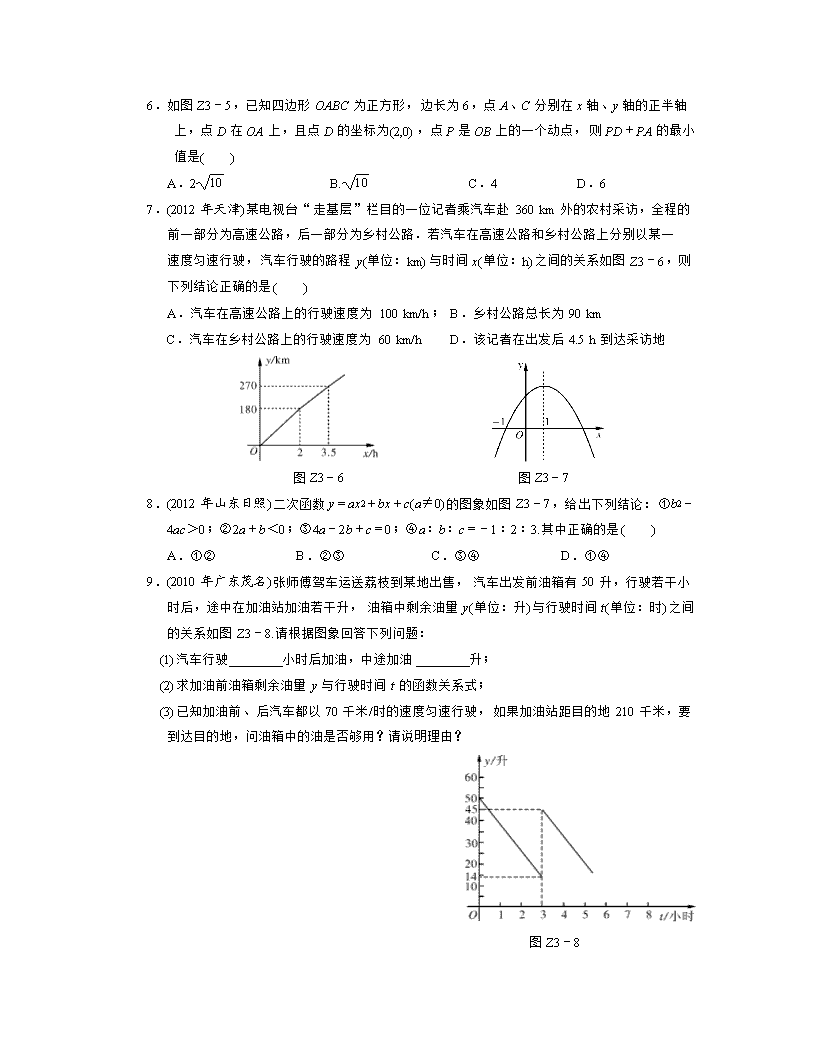C．4 D．6‎ ‎7．(2012年天津)某电视台“走基层”栏目的一位记者乘汽车赴‎360 km外的农村采访，全程的前一部分为高速公路，后一部分为乡村公路．若汽车在高速公路和乡村公路上分别以某一速度匀速行驶，汽车行驶的路程y(单位：km)与时间x(单位：h)之间的关系如图Z3－6，则下列结论正确的是(　　)‎ A．汽车在高速公路上的行驶速度为‎100 km/h； B．乡村公路总长为‎90 km C．汽车在乡村公路上的行驶速度为‎60 km/h D．该记者在出发后4.5 h到达采访地 ‎ ‎ 图Z3－6 图Z3－7‎ ‎8．(2012年山东日照)二次函数y＝ax2＋bx＋c(a≠0)的图象如图Z3－7，给出下列结论：①b2－‎4ac＞0；②‎2a＋b＜0；③‎4a－2b＋c＝0；④a∶b∶c＝－1∶2∶3.其中正确的是(　　)‎ A．①② B．②③ C．③④ D．①④‎ ‎9．(2010年广东茂名)张师傅驾车运送荔枝到某地出售，汽车出发前油箱有‎50升，行驶若干小时后，途中在加油站加油若干升，油箱中剩余油量y(单位：升)与行驶时间t(单位：时)之间的关系如图Z3－8.请根据图象回答下列问题：‎ ‎(1)汽车行驶________小时后加油，中途加油________升；‎ ‎(2)求加油前油箱剩余油量y与行驶时间t的函数关系式；‎ ‎(3)已知加油前、后汽车都以70千米/时的速度匀速行驶，如果加油站距目的地210千米，要到达目的地，问油箱中的油是否够用？请说明理由？‎ ‎ 图Z3－8‎ ‎10．(2011年湖南邵阳)如图Z3－9，在平面直角坐标系xOy中，已知点A，点C(0,3)，点B是x轴上的一点(位于点A右侧)，以AB为直径的圆恰好经过点C.‎ ‎(1)求∠ACB的度数；‎ ‎(2)已知抛物线y＝ax2＋bx＋3经过A，B两点，求抛物线的解析式；‎ ‎(3)线段BC上是否存在点D，使△BOD为等腰三角形？若存在，则求出所有符合条件的点D的坐标；若不存在，请说明理由．‎ ‎ 图Z3－9‎ ‎11．(2012年四川宜宾)如图Z3－10，抛物线y＝x2－2x＋c的顶点A在直线l∶y＝x－5上．‎ ‎(1)求抛物线顶点A的坐标；‎ ‎(2)设抛物线与y轴交于点B，与x轴交于点C，D(点C在点D的左侧)，试判断△ABD的形状；‎ ‎(3)在直线l上是否存在一点P，使以点P，A，B，D为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由．‎ ‎ 图Z3－10‎ 参考答案 ‎1．A　2.B　3.D　4.A　5.B　6.A　7.C ‎8．D ‎9．解：(1)3　31‎ ‎(2)设y与t的函数关系式是y＝kt＋b(k≠0)，‎ 根据题意，得 解得k＝－12，b＝50.‎ 因此，加油前油箱剩余油量y与行驶时间t的函数关系式是y＝－12t＋50.‎ ‎(3)由图可知：汽车每小时用油(50－14)÷3＝12(升)，所以汽车要准备油(210÷70)×12＝36(升)．‎ 因为‎45升>‎36升，所以油箱中的油够用．‎ ‎10．解：(1)如图D60，∠ACB＝90°.‎ ‎(2)∵△AOC∽△COB，‎ 图D60‎ ‎∴＝.‎ 又∵A，C(0,3)，‎ ‎∴ AO＝，OC＝3.‎ ‎∴解得OB＝4.‎ ‎∴B(4,0)．把 A，B两点坐标代入解得：‎ y＝－x2＋x＋3.‎ ‎(3)存在．‎ 直线BC的方程为3x＋4y＝12，设点D(x，y)．‎ ‎①若BD＝OD，则点D在OB的中垂线上，点D的横坐标为2，纵坐标为，即点D1(2，)为所求．‎ ‎②若OB＝BD＝4，则＝，＝，得y＝，x＝，点D2(，)为所求．‎ ‎11．解：(1)∵顶点A的横坐标为x＝－＝1，且顶点A在y＝x－5上，‎ ‎∴当x＝1时，y＝1－5＝－4.‎ ‎∴A(1，－4)．‎ ‎(2)△ABD是直角三角形．‎ 将A(1，－4)代入y＝x2－2x＋c，‎ 可得1－2＋c＝－4，∴c＝－3.‎ ‎∴y＝x2－2x－3.∴B(0，－3)．‎ 当y＝0时，x2－2x－3＝0，x1＝－1，x2＝3，‎ ‎∴C(－1,0)，D(3,0)．‎ ‎∵BD2＝OB2＋OD2＝18，AB2＝(4－3)2＋12＝2，AD2＝(3－1)2＋42＝20，‎ ‎∴BD2＋AB2＝AD2.‎ ‎∴∠ABD＝90°，即△ABD是直角三角形．‎ ‎(3)存在．‎ 由题意知：直线y＝x－5交y轴于点E(0，－5)，交x轴于点F(5,0)．∴OE＝OF＝5.又∵OB＝OD＝3，‎ ‎∴△OEF与△OBD都是等腰直角三角形．‎ ‎∴BD∥l，即PA∥BD.‎ 则构成平行四边形只能是PADB或PABD，如图D61，‎ 图D61‎ 过点P作y轴的垂线，过点A作x轴的垂线交过P且平行于x轴的直线于点G.‎ 设P(x1，x1－5)，则G(1，x1－5)．‎ 则PG＝，AG＝＝.‎ PA＝BD＝3 ，‎ 由勾股定理，得：‎ ‎(1－x1)2＋(1－x1)2＝18，‎ x－2x1－8＝0，x1＝－2或4.‎ ‎∴P(－2，－7)或P(4，－1)．‎ 存在点P(－2，－7)或P(4，－1)使以点A，B，D，P为顶点的四边形是平行四边形．‎