中考数学100份试卷分类汇编圆的综合题 28页

‎2013中考全国100份试卷分类汇编 圆的综合题 ‎1、（2013•温州）在△ABC中，∠C为锐角，分别以AB，AC为直径作半圆，过点B，A，C作，如图所示．若AB=4，AC=2，S1﹣S2=，则S3﹣S4的值是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 圆的认识 分析：‎ 首先根据AB、AC的长求得S1+S3和S2+S4的值，然后两值相减即可求得结论．‎ 解答：‎ 解：∵AB=4，AC=2，‎ ‎∴S1+S3=2π，S2+S4=，‎ ‎∵S1﹣S2=，‎ ‎∴（S1+S3）﹣（S2+S4）=（S1﹣S2）+（S3﹣S4）=π ‎∴S3﹣S4=π，‎ 故选D．‎ 点评：‎ 本题考查了圆的认识，解题的关键是正确的表示出S1+S3和S2+S4的值．‎ ‎2、（2013•孝感）下列说法正确的是（　　）‎ ‎　‎ A．‎ 平分弦的直径垂直于弦 ‎　‎ B．‎ 半圆（或直径）所对的圆周角是直角 ‎　‎ C．‎ 相等的圆心角所对的弧相等 ‎　‎ D．‎ 若两个圆有公共点，则这两个圆相交 考点：‎ 圆与圆的位置关系；垂径定理；圆心角、弧、弦的关系；圆周角定理．‎ 分析：‎ 利用圆与圆的位置关系、垂径定理、圆周角定理等有关圆的知识进行判断即可 解答：‎ 解：A、平分弦（不是直径）的直径垂直于弦，故本选项错误；‎ B、半圆或直径所对的圆周角是直角，故本选项正确；‎ C、同圆或等圆中，相等的圆心角所对的弧相等，故本选项错误；‎ D、两圆有两个公共点，两圆相交，故本选项错误，‎ 故选B．‎ 点评：‎ 本题考查了圆与圆的位置关系、垂径定理、圆周角定理等有关圆的知识，牢记这些定理是解决本题的关键．‎ ‎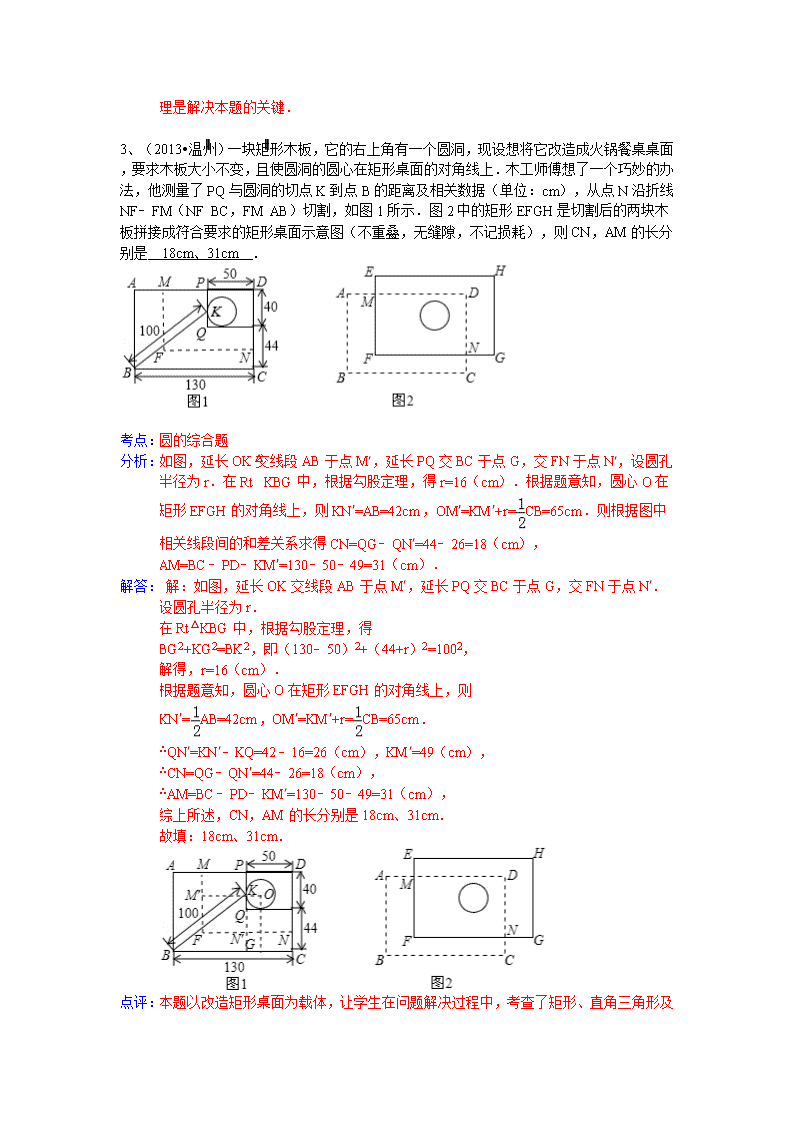3、（2013•温州）一块矩形木板，它的右上角有一个圆洞，现设想将它改造成火锅餐桌桌面，要求木板大小不变，且使圆洞的圆心在矩形桌面的对角线上．木工师傅想了一个巧妙的办法，他测量了PQ与圆洞的切点K到点B的距离及相关数据（单位：cm），从点N沿折线NF﹣FM（NF∥BC，FM∥AB）切割，如图1所示．图2中的矩形EFGH是切割后的两块木板拼接成符合要求的矩形桌面示意图（不重叠，无缝隙，不记损耗），则CN，AM的长分别是　18cm、31cm　．‎ 考点：‎ 圆的综合题 分析：‎ 如图，延长OK交线段AB于点M′，延长PQ交BC于点G，交FN于点N′，设圆孔半径为r．在Rt△KBG中，根据勾股定理，得r=16（cm）．根据题意知，圆心O在矩形EFGH的对角线上，则KN′=AB=42cm，OM′=KM′+r=CB=65cm．则根据图中相关线段间的和差关系求得CN=QG﹣QN′=44﹣26=18（cm），AM=BC﹣PD﹣KM′=130﹣50﹣49=31（cm）．‎ 解答：‎ ‎ 解：如图，延长OK交线段AB于点M′，延长PQ交BC于点G，交FN于点N′．‎ 设圆孔半径为r．‎ 在Rt△KBG中，根据勾股定理，得 BG2+KG2=BK2，即（130﹣50）2+（44+r）2=1002，‎ 解得，r=16（cm）．‎ 根据题意知，圆心O在矩形EFGH的对角线上，则 ‎ KN′=AB=42cm，OM′=KM′+r=CB=65cm．‎ ‎∴QN′=KN′﹣KQ=42﹣16=26（cm），KM′=49（cm），‎ ‎∴CN=QG﹣QN′=44﹣26=18（cm），‎ ‎∴AM=BC﹣PD﹣KM′=130﹣50﹣49=31（cm），‎ 综上所述，CN，AM的长分别是18cm、31cm．‎ 故填：18cm、31cm．‎ 点评：‎ 本题以改造矩形桌面为载体，让学生在问题解决过程中，考查了矩形、直角三角形及圆等相关知识，积累了将实际问题转化为数学问题经验，渗透了图形变换思想，体现了数学思想方法在现实问题中的应用价值．‎ ‎4、（2013四川宜宾）如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足=，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2，AF=3．给出下列结论：①△ADF∽△AED；②FG=2；③tan∠E=；④S△DEF=4．‎ 其中正确的是　①②④　（写出所有正确结论的序号）．‎ 考点：相似三角形的判定与性质；垂径定理；圆周角定理．‎ 分析：①由AB是⊙O的直径，弦CD⊥AB，根据垂径定理可得：=，DG=CG，继而证得△ADF∽△AED；‎ ‎②由=，CF=2，可求得DF的长，继而求得CG=DG=4，则可求得FG=2；‎ ‎③由勾股定理可求得AG的长，即可求得tan∠ADF的值，继而求得tan∠E=；‎ ‎④首先求得△ADF的面积，由相似三角形面积的比等于相似比，即可求得△ADE的面积，继而求得S△DEF=4．‎ 解答：解：①∵AB是⊙O的直径，弦CD⊥AB，‎ ‎∴=，DG=CG，‎ ‎∴∠ADF=∠AED，‎ ‎∵∠FAD=∠DAE（公共角），‎ ‎∴△ADF∽△AED；‎ 故①正确；‎ ‎②∵=，CF=2，‎ ‎∴FD=6，‎ ‎∴CD=DF+CF=8，‎ ‎∴CG=DG=4，‎ ‎∴FG=CG﹣CF=2；‎ 故②正确；‎ ‎③∵AF=3，FG=2，‎ ‎∴AG==，‎ ‎∴在Rt△AGD中，tan∠ADG==，‎ ‎∴tan∠E=；‎ 故③错误；‎ ‎④∵DF=DG+FG=6，AD==，‎ ‎∴S△ADF=DF•AG=×6×=3，‎ ‎∵△ADF∽△AED，‎ ‎∴=（）2，‎ ‎∴=，‎ ‎∴S△AED=7，‎ ‎∴S△DEF=S△AED﹣S△ADF=4；‎ 故④正确．‎ 故答案为：①②④．‎ 点评：此题考查了相似三角形的判定与性质、圆周角定理、垂径定理、勾股定理以及三角函数等知识．此题综合性较强，难度适中，注意掌握数形结合思想的应用．　‎ ‎5、(2013年武汉)如图，在平面直角坐标系中，△ABC是⊙O的内接三角形，AB＝AC，点P是的中点，连接PA，PB，PC． ‎ ‎（1）如图①，若∠BPC＝60°，求证：；‎ ‎（2）如图②，若，求的值．‎ 解析：‎ ‎（1）证明：∵弧BC＝弧BC，∴∠BAC＝∠BPC＝60°．‎ 又∵AB＝AC，∴△ABC为等边三角形 ‎∴∠ACB＝60°，∵点P是弧AB的中点，∴∠ACP＝30°，‎ 又∠APC＝∠ABC＝60°，∴AC＝AP．‎ ‎（2）解：连接AO并延长交PC于F，过点E作EG⊥AC于G，连接OC．‎ ‎ ∵AB＝AC，∴AF⊥BC，BF＝CF．‎ ‎ ∵点P是弧AB中点，∴∠ACP＝∠PCB，∴EG＝EF．‎ ‎ ∵∠BPC＝∠FOC，‎ ‎∴sin∠FOC＝sin∠BPC=．‎ 设FC＝‎24a，则OC＝OA＝‎25a，‎ ‎∴OF＝‎7a，AF＝‎32a．‎ ‎ 在Rt△AFC中，AC2＝AF2+FC2，∴AC＝‎40a．‎ 在Rt△AGE和Rt△AFC中，sin∠FAC＝，‎ ‎∴，∴EG＝‎12a．‎ ‎∴tan∠PAB＝tan∠PCB=． ‎ ‎6、（2013•常州）在平面直角坐标系xOy中，已知点A（6，0），点B（0，6），动点C在以半径为3的⊙O上，连接OC，过O点作OD⊥OC，OD与⊙O相交于点D（其中点C、O、D按逆时针方向排列），连接AB．‎ ‎（1）当OC∥AB时，∠BOC的度数为　45°或135°　；‎ ‎（2）连接AC，BC，当点C在⊙O上运动到什么位置时，△ABC的面积最大？并求出△ABC的面积的最大值．‎ ‎（3）连接AD，当OC∥AD时，‎ ‎①求出点C的坐标；②直线BC是否为⊙O的切线？请作出判断，并说明理由．‎ 考点：‎ 圆的综合题．3718684‎ 专题：‎ 综合题．‎ 分析：‎ ‎（1）根据点A和点B坐标易得△OAB为等腰直角三角形，则∠OBA=45°，由于OC∥AB，所以当C点在y轴左侧时，有∠BOC=∠OBA=45°；当C点在y轴右侧时，有∠BOC=180°﹣∠OBA=135°；‎ ‎（2）由△OAB为等腰直角三角形得AB=OA=6，根据三角形面积公式得到当点C到AB的距离最大时，△ABC的面积最大，过O点作OE⊥AB于E，OE的反向延长线交⊙O于C，‎ 此时C点到AB的距离的最大值为CE的长然后利用等腰直角三角形的性质计算出OE，然后计算△ABC的面积；‎ ‎（3）①过C点作CF⊥x轴于F，易证Rt△OCF∽Rt△AOD，则=，即=，解得CF=，再利用勾股定理计算出OF=，则可得到C点坐标；‎ ‎②由于OC=3，OF=，所以∠COF=30°，则可得到∴BOC=60°，∠AOD=60°，然后根据“SAS”判断△BOC≌△AOD，所以∠BCO=∠ADC=90°，再根据切线的判定定理可确定 直线BC为⊙O的切线．‎ 解答：‎ 解：（1）∵点A（6，0），点B（0，6），‎ ‎∴OA=OB=6，‎ ‎∴△OAB为等腰直角三角形，‎ ‎∴∠OBA=45°，‎ ‎∵OC∥AB，‎ ‎∴当C点在y轴左侧时，∠BOC=∠OBA=45°；当C点在y轴右侧时，∠BOC=180°﹣∠OBA=135°；‎ ‎（2）∵△OAB为等腰直角三角形，‎ ‎∴AB=OA=6，‎ ‎∴当点C到AB的距离最大时，△ABC的面积最大，‎ 过O点作OE⊥AB于E，OE的反向延长线交⊙O于C，如图，此时C点到AB的距离的最大值为CE的长，‎ ‎∵△OAB为等腰直角三角形，‎ ‎∴AB=OA=6，‎ ‎∴OE=AB=3，‎ ‎∴CE=OC+CE=3+3，△ABC的面积=CE•AB=×（3+3）×6=9+18．‎ ‎∴当点C在⊙O上运动到第三象限的角平分线与圆的交点位置时，△ABC的面积最大，最大值为9+18．‎ ‎（3）①如图，过C点作CF⊥x轴于F，‎ ‎∵OC∥AD，‎ ‎∴∠ADO=∠COD=90°，‎ ‎∴∠DOA+∠DAO=90°‎ 而∠DOA+∠COF=90°，‎ ‎∴∠COF=∠DAO，‎ ‎∴Rt△OCF∽Rt△AOD，‎ ‎∴=，即=，解得CF=，‎ 在Rt△OCF中，OF==，‎ ‎∴C点坐标为（﹣，）；‎ ‎②直线BC是⊙O的切线．理由如下：‎ 在Rt△OCF中，OC=3，OF=，‎ ‎∴∠COF=30°，‎ ‎∴∠OAD=30°，‎ ‎∴∠BOC=60°，∠AOD=60°，‎ ‎∵在△BOC和△AOD中 ‎，‎ ‎∴△BOC≌△AOD（SAS），‎ ‎∴∠BCO=∠ADC=90°，‎ ‎∴OC⊥BC，‎ ‎∴直线BC为⊙O的切线．‎ 点评：‎ 本题考查了圆的综合题：掌握切线的判定定理、平行线的性质和等腰直角三角形的判定与性质；熟练运用勾股定理和相似比进行几何计算．‎ ‎　‎ ‎7、（2013•宜昌）半径为‎2cm的与⊙O边长为‎2cm的正方形ABCD在水平直线l的同侧，⊙O与l相切于点F，DC在l上．‎ ‎（1）过点B作的一条切线BE，E为切点．‎ ‎①填空：如图1，当点A在⊙O上时，∠EBA的度数是　30°　；‎ ‎②如图2，当E，A，D三点在同一直线上时，求线段OA的长；‎ ‎（2）以正方形ABCD的边AD与OF重合的位置为初始位置，向左移动正方形（图3），至边BC与OF重合时结束移动，M，N分别是边BC，AD与⊙O的公共点，求扇形MON的面积的范围．‎ 考点：‎ 圆的综合题．‎ 分析：‎ ‎（1）①根据切线的性质以及直角三角形的性质得出∠EBA的度数即可；‎ ‎②利用切线的性质以及矩形的性质和相似三角形的判定和性质得出=，进而求出OA即可；‎ ‎（2）设∠MON=n°，得出S扇形MON=×22=n进而利用函数增减性分析①当N，M，A分别与D，B，O重合时，MN最大，②当MN=DC=2时，MN最小，分别求出即可．‎ 解答：‎ 解：（1）①∵半径为‎2cm的与⊙O边长为‎2cm的正方形ABCD在水平直线l的同侧，当点A在⊙O上时，过点B作的一条切线BE，E为切点，‎ ‎∴OB=4，EO=2，∠OEB=90°，‎ ‎∴∠EBA的度数是：30°；‎ ‎②如图2，‎ ‎∵直线l与⊙O相切于点F，‎ ‎∴∠OFD=90°，‎ ‎∵正方形ADCB中，∠ADC=90°，‎ ‎∴OF∥AD，‎ ‎∵OF=AD=2，‎ ‎∴四边形OFDA为平行四边形，‎ ‎∵∠OFD=90°，‎ ‎∴平行四边形OFDA为矩形，‎ ‎∴DA⊥AO，‎ ‎∵正方形ABCD中，DA⊥AB，‎ ‎∴O，A，B三点在同一条直线上；‎ ‎∴EA⊥OB，‎ ‎∵∠OEB=∠AOE，‎ ‎∴△EOA∽△BOE，‎ ‎∴=，‎ ‎∴OE2=OA•OB，‎ ‎∴OA（2+OA）=4，‎ 解得：OA=﹣1±，‎ ‎∵OA＞0，∴OA=﹣1；‎ 方法二：‎ 在Rt△OAE中，cos∠EOA==，‎ 在Rt△EOB中，cos∠EOB==，‎ ‎∴=，‎ 解得：OA=﹣1±，‎ ‎∵OA＞0，∴OA=﹣1；‎ 方法三：‎ ‎∵OE⊥EB，EA⊥OB，‎ ‎∴由射影定理，得OE2=OA•OB，‎ ‎∴OA（2+OA）=4，‎ 解得：OA=﹣1±，‎ ‎∵OA＞0，‎ ‎∴OA=﹣1；‎ ‎（2）如图3，设∠MON=n°，S扇形MON=×22=n（cm2），‎ S随n的增大而增大，∠MON取最大值时，S扇形MON最大，‎ 当∠MON取最小值时，S扇形MON最小，‎ 过O点作OK⊥MN于K，‎ ‎∴∠MON=2∠NOK，MN=2NK，‎ 在Rt△ONK中，sin∠NOK==，‎ ‎∴∠NOK随NK的增大而增大，∴∠MON随MN的增大而增大，‎ ‎∴当MN最大时∠MON最大，当MN最小时∠MON最小，‎ ‎①当N，M，A分别与D，B，O重合时，MN最大，MN=BD，‎ ‎∠MON=∠BOD=90°，S扇形MON最大=π（cm2），‎ ‎②当MN=DC=2时，MN最小，‎ ‎∴ON=MN=OM，‎ ‎∴∠NOM=60°，‎ S扇形MON最小=π（cm2），‎ ‎∴π≤S扇形MON≤π．‎ 故答案为：30°．‎ 点评：‎ 此题主要考查了圆的综合应用以及相似三角形的判定与性质和函数增减性等知识，得出扇形MON的面积的最大值与最小值是解题关键．‎ ‎8、（2013•包头）如图，已知在△ABP中，C是BP边上一点，∠PAC=∠PBA，⊙O是△ABC的外接圆，AD是⊙O的直径，且交BP于点E．‎ ‎（1）求证：PA是⊙O的切线；‎ ‎（2）过点C作CF⊥AD，垂足为点F，延长CF交AB于点G，若AG•AB=12，求AC的长；‎ ‎（3）在满足（2）的条件下，若AF：FD=1：2，GF=1，求⊙O的半径及sin∠ACE的值．‎ 考点：‎ 圆的综合题．3718684‎ 分析：‎ ‎（1）根据圆周角定理得出∠ACD=90°以及利用∠PAC=∠PBA得出∠CAD+∠PAC=90°进而得出答案；‎ ‎（2）首先得出△CAG∽△BAC，进而得出AC2=AG•AB，求出AC即可；‎ ‎（3）先求出AF的长，根据勾股定理得：AG=，即可得出sin∠ADB=，利用∠ACE=∠ACB=∠ADB，求出即可．‎ 解答：‎ ‎（1）证明：连接CD，‎ ‎∵AD是⊙O的直径，‎ ‎∴∠ACD=90°，‎ ‎∴∠CAD+∠ADC=90°，‎ 又∵∠PAC=∠PBA，∠ADC=∠PBA，‎ ‎∴∠PAC=∠ADC，‎ ‎∴∠CAD+∠PAC=90°，‎ ‎∴PA⊥OA，而AD是⊙O的直径，‎ ‎∴PA是⊙O的切线；‎ ‎（2）解：由（1）知，PA⊥AD，又∵CF⊥AD，∴CF∥PA，‎ ‎∴∠GCA=∠PAC，又∵∠PAC=∠PBA，‎ ‎∴∠GCA=∠PBA，而∠CAG=∠BAC，‎ ‎∴△CAG∽△BAC，‎ ‎∴=，‎ 即AC2=AG•AB，‎ ‎∵AG•AB=12，‎ ‎∴AC2=12，‎ ‎∴AC=2；‎ ‎（3）解：设AF=x，∵AF：FD=1：2，∴FD=2x，‎ ‎∴AD=AF+FD=3x，‎ 在Rt△ACD中，∵CF⊥AD，∴AC2=AF•AD，‎ 即3x2=12，‎ 解得；x=2，‎ ‎∴AF=2，AD=6，∴⊙O半径为3，‎ 在Rt△AFG中，∵AF=2，GF=1，‎ 根据勾股定理得：AG===，‎ 由（2）知，AG•AB=12，‎ ‎∴AB==，‎ 连接BD，‎ ‎∵AD是⊙O的直径，‎ ‎∴∠ABD=90°，‎ 在Rt△ABD中，∵sin∠ADB=，AD=6，‎ ‎∴sin∠ADB=，‎ ‎∵∠ACE=∠ACB=∠ADB，‎ ‎∴sin∠ACE=．‎ 点评：‎ 此题主要考查了圆的综合应用以及勾股定理和锐角三角函数关系等知识，根据已知得出AG的长以及AB的长是解题关键．‎ ‎9、（2013•荆门）如图1，正方形ABCD的边长为2，点M是BC的中点，P是线段MC上的一个动点（不与M、C重合），以AB为直径作⊙O，过点P作⊙O的切线，交AD于点F，切点为E．‎ ‎（1）求证：OF∥BE；‎ ‎（2）设BP=x，AF=y，求y关于x的函数解析式，并写出自变量x的取值范围；‎ ‎（3）延长DC、FP交于点G，连接OE并延长交直线DC与H（图2），问是否存在点P，使△EFO∽△EHG（E、F、O与E、H、G为对应点）？如果存在，试求（2）中x和y的值；如果不存在，请说明理由．‎ 考点：‎ 圆的综合题．3718684‎ 分析：‎ ‎（1）首先证明Rt△FAO≌Rt△FEO进而得出∠AOF=∠ABE，即可得出答案；‎ ‎（2）过F作FQ⊥BC于Q，利用勾股定理求出y与x之间的函数关系，根据M是BC中点以及BC=2，即可得出BP的取值范围；‎ ‎（3）首先得出当∠EFO=∠EHG=2∠EOF时，即∠EOF=30°时，Rt△EFO∽Rt△EHG，求出y=AF=OA•tan30°=，即可得出答案．‎ 解答：‎ ‎（1）证明：连接OE FE、FA是⊙O的两条切线 ‎∴∠FAO=∠FEO=90°‎ 在Rt△OAF和Rt△OEF中，‎ ‎∴Rt△FAO≌Rt△FEO（HL），‎ ‎∴∠AOF=∠EOF=∠AOE，‎ ‎∴∠AOF=∠ABE，‎ ‎∴OF∥BE，‎ ‎（2）解：过F作FQ⊥BC于Q ‎∴PQ=BP﹣BQ=x﹣y PF=EF+EP=FA+BP=x+y ‎∵在Rt△PFQ中 ‎∴FQ2+QP2=PF2‎ ‎∴22+（x﹣y）2=（x+y）2‎ 化简得：，（1＜x＜2）；‎ ‎（3）存在这样的P点，‎ 理由：∵∠EOF=∠AOF，‎ ‎∴∠EHG=∠EOA=2∠EOF，‎ 当∠EFO=∠EHG=2∠EOF时，‎ 即∠EOF=30°时，Rt△EFO∽Rt△EHG，‎ 此时Rt△AFO中，‎ y=AF=OA•tan30°=，‎ ‎∴‎ ‎∴当时，△EFO∽△EHG．‎ 点评：‎ 此题主要考查了圆的综合应用以及全等三角形的判定和性质以及相似三角形的判定与性质等知识，得出FQ2+QP2=PF2是解题关键．‎ ‎10、（2013•莱芜）如图，⊙O的半径为1，直线CD经过圆心O，交⊙O于C、D两点，直径AB⊥CD，点M是直线CD上异于点C、O、D的一个动点，AM所在的直线交于⊙O于点N，点P是直线CD上另一点，且PM=PN．‎ ‎（1）当点M在⊙O内部，如图一，试判断PN与⊙O的关系，并写出证明过程；‎ ‎（2）当点M在⊙O外部，如图二，其它条件不变时，（1）的结论是否还成立？请说明理由；‎ ‎（3）当点M在⊙O外部，如图三，∠AMO=15°，求图中阴影部分的面积．‎ 考点：‎ 圆的综合题．‎ 分析：‎ ‎（1）根据切线的判定得出∠PNO=∠PNM+∠ONA=∠AMO+∠ONA进而求出即可；‎ ‎（2）根据已知得出∠PNM+∠ONA=90°，进而得出∠PNO=180°﹣90°=90°即可得出答案；‎ ‎（3）首先根据外角的性质得出∠AON=30°进而利用扇形面积公式得出即可．‎ 解答：‎ ‎（1）PN与⊙O相切．‎ 证明：连接ON，‎ 则∠ONA=∠OAN，‎ ‎∵PM=PN，∴∠PNM=∠PMN．‎ ‎∵∠AMO=∠PMN，∴∠PNM=∠AMO．‎ ‎∴∠PNO=∠PNM+∠ONA=∠AMO+∠ONA=90°．‎ 即PN与⊙O相切．‎ ‎（2）成立．‎ 证明：连接ON，‎ 则∠ONA=∠OAN，‎ ‎∵PM=PN，∴∠PNM=∠PMN．‎ 在Rt△AOM中，‎ ‎∴∠OMA+∠OAM=90°，‎ ‎∴∠PNM+∠ONA=90°．‎ ‎∴∠PNO=180°﹣90°=90°．‎ 即PN与⊙O相切．‎ ‎（3）解：连接ON，由（2）可知∠ONP=90°．‎ ‎∵∠AMO=15°，PM=PN，∴∠PNM=15°，∠OPN=30°，‎ ‎∵∠PON=60°，∠AON=30°．‎ 作NE⊥OD，垂足为点E，‎ 则NE=ON•sin60°=1×=．‎ S阴影=S△AOC+S扇形AON﹣S△CON=OC•OA+CO•NE ‎=×1×1+π﹣×1×‎ ‎=+π﹣．‎ 点评：‎ 此题主要考查了扇形面积公式以及切线的判定等知识，熟练根据切线的判定得出对应角的度数是解题关键．‎ ‎11、（2013•遂宁）如图，在⊙O中，直径AB⊥CD，垂足为E，点M在OC上，AM的延长线交⊙O于点G，交过C的直线于F，∠1=∠2，连结CB与DG交于点N．‎ ‎（1）求证：CF是⊙O的切线；‎ ‎（2）求证：△ACM∽△DCN；‎ ‎（3）若点M是CO的中点，⊙O的半径为4，cos∠BOC=，求BN的长．‎ 考点：‎ 圆的综合题．‎ 分析：‎ ‎（1）根据切线的判定定理得出∠1+∠BCO=90°，即可得出答案；‎ ‎（2）利用已知得出∠3=∠2，∠4=∠D，再利用相似三角形的判定方法得出即可；‎ ‎（3）根据已知得出OE的长，进而利用勾股定理得出EC，AC，BC的长，即可得出CD，利用（2）中相似三角形的性质得出NB的长即可．‎ 解答：‎ ‎（1）证明：∵△BCO中，BO=CO，‎ ‎∴∠B=∠BCO，‎ 在Rt△BCE中，∠2+∠B=90°，‎ 又∵∠1=∠2，∴∠1+∠BCO=90°，即∠FCO=90°，‎ ‎∴CF是⊙O的切线；‎ ‎（2）证明：∵AB是⊙O直径，∴∠ACB=∠FCO=90°，‎ ‎∴∠ACB﹣∠BCO=∠FCO﹣∠BCO，‎ 即∠3=∠1，∴∠3=∠2，‎ ‎∵∠4=∠D，∴△ACM∽△DCN；‎ ‎（3）解：∵⊙O的半径为4，即AO=CO=BO=4，‎ 在Rt△COE中，cos∠BOC=，‎ ‎∴OE=CO•cos∠BOC=4×=1，‎ 由此可得：BE=3，AE=5，由勾股定理可得：‎ CE===，‎ AC===2，‎ BC===2，‎ ‎∵AB是⊙O直径，AB⊥CD，‎ ‎∴由垂径定理得：CD=2CE=2，‎ ‎∵△ACM∽△DCN，‎ ‎∴=，‎ ‎∵点M是CO的中点，CM=AO=×4=2，‎ ‎∴CN===，‎ ‎∴BN=BC﹣CN=2﹣=．‎ 点评：‎ 此题主要考查了相似三角形的判定与性质以及切线的判定和勾股定理的应用等知识，根据已知得出△ACM∽△DCN是解题关键．‎ ‎12、（2013济宁）如图1，在平面直角坐标系中，O为坐标原点，P是反比例函数y=（x＞0）图象上任意一点，以P为圆心，PO为半径的圆与坐标轴分别交于点A、B．‎ ‎（1）求证：线段AB为⊙P的直径；‎ ‎（2）求△AOB的面积；‎ ‎（3）如图2，Q是反比例函数y=（x＞0）图象上异于点P的另一点，以Q为圆心，QO为半径画圆与坐标轴分别交于点C、D．‎ 求证：DO•OC=BO•OA．‎ 考点：反比例函数综合题．‎ 分析：（1）∠AOB=90°，由圆周角定理的推论，可以证明AB是⊙P的直径；‎ ‎（2）将△AOB的面积用含点P坐标的表达式表示出来，容易计算出结果；‎ ‎（3）对于反比例函数上另外一点Q，⊙Q与坐标轴所形成的△COD的面积，依然不变，与△AOB的面积相等．‎ 解答：（1）证明：∵∠AOB=90°，且∠AOB是⊙P中弦AB所对的圆周角，‎ ‎∴AB是⊙P的直径．‎ ‎（2）解：设点P坐标为（m，n）（m＞0，n＞0），‎ ‎∵点P是反比例函数y=（x＞0）图象上一点，∴mn=12．‎ 如答图，过点P作PM⊥x轴于点M，PN⊥y轴于点N，则OM=m，ON=n．‎ 由垂径定理可知，点M为OA中点，点N为OB中点，‎ ‎∴OA=2OM=‎2m，OB=2ON=2n，‎ ‎∴S△AOB=BO•OA=×2n×‎2m=2mn=2×12=24．‎ ‎（3）证明：若点Q为反比例函数y=（x＞0）图象上异于点P的另一点，‎ 参照（2），同理可得：S△COD=DO•CO=24，‎ 则有：S△COD=S△AOB=24，即BO•OA=DO•CO，‎ ‎∴DO•OC=BO•OA．‎ 点评：本题考查了反比例函数的图象与性质、圆周角定理、垂径定理等知识，难度不大．试题的核心是考查反比例函数系数的几何意义．对本题而言，若反比例函数系数为k，则可以证明⊙P在坐标轴上所截的两条线段的乘积等于4k；对于另外一点Q所形成的⊙Q，此结论依然成立．　‎ ‎13、（2013•攀枝花）如图，PA为⊙O的切线，A为切点，直线PO交⊙O与点E，F过点A作PO的垂线AB垂足为D，交⊙O与点B，延长BO与⊙O交与点C，连接AC，BF．‎ ‎（1）求证：PB与⊙O相切；‎ ‎（2）试探究线段EF，OD，OP之间的数量关系，并加以证明；‎ ‎（3）若AC=12，tan∠F=，求cos∠ACB的值．‎ 考点：‎ 圆的综合题．‎ 分析：‎ ‎（1）连接OA，由OP垂直于AB，利用垂径定理得到D为AB的中点，即OP垂直平分AB，可得出AP=BP，再由OA=OB，OP=OP，利用SSS得出三角形AOP与三角形BOP全等，由PA为圆的切线，得到OA垂直于AP，利用全等三角形的对应角相等及垂直的定义得到OB垂直于BP，即PB为圆O的切线；‎ ‎（2）由一对直角相等，一对公共角，得出三角形AOD与三角形OAP相似，由相似得比例，列出关系式，由OA为EF的一半，等量代换即可得证．‎ ‎（3）连接BE，构建直角△BEF．在该直角三角形中利用锐角三角函数的定义、勾股定理可设BE=x，BF=2x，进而可得EF=x；然后由面积法求得BD=x，所以根据垂径定理求得AB的长度，在Rt△ABC中，根据勾股定理易求BC的长；最后由余弦三角函数的定义求解．‎ 解答：‎ ‎（1）证明：连接OA，‎ ‎∵PA与圆O相切，‎ ‎∴PA⊥OA，即∠OAP=90°，‎ ‎∵OP⊥AB，‎ ‎∴D为AB中点，即OP垂直平分AB，‎ ‎∴PA=PB，‎ ‎∵在△OAP和△OBP中，‎ ‎，‎ ‎∴△OAP≌△OBP（SSS），‎ ‎∴∠OAP=∠OBP=90°，‎ ‎∴BP⊥OB，‎ 则直线PB为圆O的切线；‎ ‎（2）答：EF2=4DO•PO．‎ 证明：∵∠OAP=∠ADO=90°，∠AOD=∠POA，‎ ‎∴△OAD∽△OPA，‎ ‎∴=，即OA2=OD•OP，‎ ‎∵EF为圆的直径，即EF=2OA，‎ ‎∴EF2=OD•OP，即EF2=4OD•OP；‎ ‎（3）解：连接BE，则∠FBE=90°．‎ ‎∵tan∠F=，‎ ‎∴=，‎ ‎∴可设BE=x，BF=2x，‎ 则由勾股定理，得 EF==x，‎ ‎∵BE•BF=EF•BD，‎ ‎∴BD=x．‎ 又∵AB⊥EF，‎ ‎∴AB=2BD=x，‎ ‎∴Rt△ABC中，BC=x，‎ AC2+AB2=BC2，‎ ‎∴122+（x）2=（x）2，‎ 解得：x=4，‎ ‎∴BC=4×=20，‎ ‎∴cos∠ACB===．‎ 点评：‎ 此题考查了切线的判定与性质，相似及全等三角形的判定与性质以及锐角三角函数关系等知识，熟练掌握切线的判定与性质是解本题的关键．‎ ‎14、(2013年南京)如图，AD是圆O的切线，切点为A，AB是圆O ‎ 的弦。过点B作BC//AD，交圆O于点C，连接AC，过 ‎ 点C作CD//AB，交AD于点D。连接AO并延长交BC A B C D O M P ‎ 于点M，交过点C的直线于点P，且ÐBCP=ÐACD。‎ ‎ (1) 判断直线PC与圆O的位置关系，并说明理由：‎ ‎ (2) 若AB=9，BC=6，求PC的长。‎ 解析： 解法一：(1) 直线PC与圆O相切。‎ j A B C D O M P N ‎ 如图j，连接CO并延长，交圆O于点N，连接BN。‎ ‎ ∵AB//CD，∴ÐBAC=ÐACD。‎ ‎ ∵ÐBAC=ÐBNC，∴ÐBNC=ÐACD。‎ ‎ ∵ÐBCP=ÐACD，∴ÐBNC=ÐBCP。‎ ‎ ∵CN是圆O的直径，∴ÐCBN=90°。‎ ‎ ∴ÐBNC+ÐBCN=90°，∴ÐBCP+ÐBCN=90°。‎ ‎ ∴ÐPCO=90°，即PC^OC。‎ ‎ 又点C在圆O上，∴直线PC与圆O相切。 (4分)‎ ‎ ‎ ‎ (2) ∵AD是圆O的切线，∴AD^OA，即ÐOAD=90°。‎ ‎ ∵BC//AD，∴ÐOMC=180°-ÐOAD=90°，即OM^BC。‎ ‎ ∴MC=MB。∴AB=AC。‎ ‎ 在Rt△AMC中，ÐAMC=90°，AC=AB=9，MC= BC=3，‎ ‎ 由勾股定理，得AM===6。‎ ‎ 设圆O的半径为r。‎ ‎ 在Rt△OMC中，ÐOMC=90°，OM=AM-AO=6-r，MC=3，OC=r，‎ ‎ 由勾股定理，得OM 2+MC 2=OC 2，即(6-r)2+32=r2。解得r= 。‎ ‎ 在△OMC和△OCP中，‎ ‎ ∵ÐOMC=ÐOCP，ÐMOC=ÐCOP，‎ ‎ ∴△OMC～△OCP。∴ = ，即 = 。‎ ‎ ∴PC= 。(8分)‎ A B C D O M P k ‎ 解法二：(1) 直线PC与圆O相切。如图k，连接OC。‎ ‎ ∵AD是圆O的切线，∴AD^OA，‎ ‎ 即ÐOAD=90°。‎ ‎ ∵BC//AD，∴ÐOMC=180°-ÐOAD=90°，‎ ‎ 即OM^BC。‎ ‎ ∴MC=MB。∴AB=AC。∴ÐMAB=ÐMAC。‎ ‎ ∴ÐBAC=2ÐMAC。又∵ÐMOC=2ÐMAC，∴ÐMOC=ÐBAC。‎ ‎ ∵AB//CD，∴ÐBAC=ÐACD。∴ÐMOC=ÐACD。又∵ÐBCP=ÐACD，‎ ‎ ∴ÐMOC=ÐBCP。∵ÐMOC+ÐOCM=90°，∴ÐBCP+ÐOCM=90°。‎ ‎ ∴ÐPCO=90°，即PC^OC。又∵点C在圆O上，∴直线PC与圆O相切。‎ ‎ (2) 在Rt△AMC中，ÐAMC=90°，AC=AB=9，MC= BC=3，‎ ‎ 由勾股定理，得AM===6。‎ ‎ 设圆O的半径为r。‎ ‎ 在Rt△OMC中，ÐOMC=90°，OM=AM-AO=6-r，MC=3，OC=r，‎ ‎ 由勾股定理，得OM 2+MC 2=OC 2，即(6-r)2+32=r2。解得r= 。‎ ‎ 在△OMC和△OCP中，∵ÐOMC=ÐOCP，ÐMOC=ÐCOP，‎ ‎ ∴△OMC～△OCP，∴ = ，即 = 。‎ ‎ ∴PC= 。(8分)‎ ‎15、（2013•曲靖）如图，⊙O的直径AB=10，C、D是圆上的两点，且．设过点D的切线ED交AC的延长线于点F．连接OC交AD于点G．‎ ‎（1）求证：DF⊥AF．‎ ‎（2）求OG的长．‎ 考点：‎ 切线的性质．‎ 分析：‎ ‎（1）连接BD，根据，可得∠CAD=∠DAB=30°，∠ABD=60°，从而可得∠AFD=90°；‎ ‎（2）根据垂径定理可得OG垂直平分AD，继而可判断OG是△ABD的中位线，在Rt△ABD中求出BD，即可得出OG．‎ 解答：‎ 解：（1）连接BD，‎ ‎∵，‎ ‎∴∠CAD=∠DAB=30°，∠ABD=60°，‎ ‎∴∠ADF=∠ABD=60°，‎ ‎∴∠CAD+∠ADF=90°，‎ ‎∴DF⊥AF．‎ ‎（2）在Rt△ABD中，∠BAD=30°，AB=10，‎ ‎∴BD=5，‎ ‎∵=，‎ ‎∴OG垂直平分AD，‎ ‎∴OG是△ABD的中位线，‎ ‎∴OG=BD=．‎ 点评：‎ 本题考查了切线的性质、圆周角定理及垂径定理的知识，解答本题要求同学们熟练掌握各定理的内容及含30°角的直角三角形的性质．‎ ‎　‎ ‎16、（2013•六盘水）（1）观察发现 ‎ 如图（1）：若点A、B在直线m同侧，在直线m上找一点P，使AP+BP的值最小，做法如下：‎ ‎ 作点B关于直线m的对称点B′，连接AB′，与直线m的交点就是所求的点P，线段AB′的长度即为AP+BP的最小值．‎ ‎ 如图（2）：在等边三角形ABC中，AB=2，点E是AB的中点，AD是高，在AD上找一点P，使BP+PE的值最小，做法如下：‎ 作点B关于AD的对称点，恰好与点C重合，连接CE交AD于一点，则这点就是所求的点P，故BP+PE的最小值为　　．‎ ‎ （2）实践运用 ‎ 如图（3）：已知⊙O的直径CD为2，的度数为60°，点B是的中点，在直径CD上作出点P，使BP+AP的值最小，则BP+AP的值最小，则BP+AP的最小值为　　．‎ ‎ （3）拓展延伸 如图（4）：点P是四边形ABCD内一点，分别在边AB、BC上作出点M，点N，使PM+PN的值最小，保留作图痕迹，不写作法．‎ 考点：‎ 圆的综合题；轴对称-最短路线问题．‎ 分析：‎ ‎（1）观察发现：利用作法得到CE的长为BP+PE的最小值；由AB=2，点E是AB的中点，根据等边三角形的性质得到CE⊥AB，∠BCE=∠BCA=30°，BE=1，再根据含30度的直角三角形三边的关系得CE=；‎ ‎（2）实践运用：过B点作弦BE⊥CD，连结AE交CD于P点，连结OB、OE、OA、PB，根据垂径定理得到CD平分BE，即点E与点B关于CD对称，则AE的长就是BP+AP的最小值；‎ 由于的度数为60°，点B是的中点得到∠BOC=30°，∠AOC=60°，所以∠AOE=60°+30°=90°，于是可判断△OAE为等腰直角三角形，则AE=OA=；‎ ‎（3）拓展延伸：分别作出点P关于AB和BC的对称点E和F，然后连结EF，EF交AB于M、交BC于N．‎ 解答：‎ 解：（1）观察发现 如图（2），CE的长为BP+PE的最小值，‎ ‎∵在等边三角形ABC中，AB=2，点E是AB的中点 ‎∴CE⊥AB，∠BCE=∠BCA=30°，BE=1，‎ ‎∴CE=BE=；‎ 故答案为；‎ ‎（2）实践运用 如图（3），过B点作弦BE⊥CD，连结AE交CD于P点，连结OB、OE、OA、PB，‎ ‎∵BE⊥CD，‎ ‎∴CD平分BE，即点E与点B关于CD对称，‎ ‎∵的度数为60°，点B是的中点，‎ ‎∴∠BOC=30°，∠AOC=60°，‎ ‎∴∠EOC=30°，‎ ‎∴∠AOE=60°+30°=90°，‎ ‎∵OA=OE=1，‎ ‎∴AE=OA=，‎ ‎∵AE的长就是BP+AP的最小值．‎ 故答案为；‎ ‎（3）拓展延伸 如图（4）．‎ 点评：‎ 本题考查了圆的综合题：弧、弦和圆心角之间的关系以及圆周角定理在有关圆的几何证明中经常用到，同时熟练掌握等边三角形的性质以及轴对称﹣最短路径问题．‎ ‎17、（2013•衡阳压轴题）如图，在平面直角坐标系中，已知A（8，0），B（0，6），⊙M经过原点O及点A、B．‎ ‎（1）求⊙M的半径及圆心M的坐标；‎ ‎（2）过点B作⊙M的切线l，求直线l的解析式；‎ ‎（3）∠BOA的平分线交AB于点N，交⊙M于点E，求点N的坐标和线段OE的长．‎ 考点：‎ 圆的综合题．‎ 专题：‎ 综合题．‎ 分析：‎ ‎（1）根据圆周角定理∠AOB=90°得AB为⊙M的直径，则可得到线段AB的中点即点M的坐标，然后利用勾股定理计算出AB=10，则可确定⊙M的半径为5；‎ ‎（2）点B作⊙M的切线l交x轴于C，根据切线的性质得AB⊥BC，利用等角的余角相等得到∠BAO=∠CBO，然后根据相似三角形的判定方法有Rt△ABO∽Rt△BCO，所以=，可解得OC=，则C点坐标为（﹣，0），最后运用待定系数法确定l的解析式；‎ ‎（3）作ND⊥x轴，连结AE，易得△NOD为等腰直角三角形，所以ND=OD，ON=ND，再利用ND∥OB得到△ADN∽△AOB，则ND：OB=AD：AO，即ND：6=（8﹣ND）：8，解得ND=，所以OD=，ON=，即可确定N点坐标；由于△ADN∽△AOB，利用ND：OB=AN：AB，可求得AN=，则BN=10﹣=，然后利用圆周角定理得∠OBA=OEA，∠BOE=∠BAE，所以△BON∽△EAN，再利用相似比可求出ME，最后由OE=ON+NE计算即可．‎ 解答：‎ 解：（1）∵∠AOB=90°，‎ ‎∴AB为⊙M的直径，‎ ‎∵A（8，0），B（0，6），‎ ‎∴OA=8，OB=6，‎ ‎∴AB==10，‎ ‎∴⊙M的半径为5；圆心M的坐标为（（4，3）；‎ ‎（2）点B作⊙M的切线l交x轴于C，如图，‎ ‎∵BC与⊙M相切，AB为直径，‎ ‎∴AB⊥BC，‎ ‎∴∠ABC=90°，‎ ‎∴∠CBO+∠ABO=90°，‎ 而∠BAO=∠ABO=90°，‎ ‎∴∠BAO=∠CBO，‎ ‎∴Rt△ABO∽Rt△BCO，‎ ‎∴=，即=，解得OC=，‎ ‎∴C点坐标为（﹣，0），‎ 设直线BC的解析式为y=kx+b，‎ 把B（0，6）、C点（﹣，0）分别代入，‎ 解得，‎ ‎∴直线l的解析式为y=x+6；‎ ‎（3）作ND⊥x轴，连结AE，如图，‎ ‎∵∠BOA的平分线交AB于点N，‎ ‎∴△NOD为等腰直角三角形，‎ ‎∴ND=OD，‎ ‎∴ND∥OB，‎ ‎∴△ADN∽△AOB，‎ ‎∴ND：OB=AD：AO，‎ ‎∴ND：6=（8﹣ND）：8，解得ND=，‎ ‎∴OD=，ON=ND=，‎ ‎∴N点坐标为（，）；‎ ‎∵△ADN∽△AOB，‎ ‎∴ND：OB=AN：AB，即：6=AN：10，解得AN=，‎ ‎∴BN=10﹣=，‎ ‎∵∠OBA=OEA，∠BOE=∠BAE，‎ ‎∴△BON∽△EAN，‎ ‎∴BN：NE=ON：AN，即：NE=：，解得NE=，‎ ‎∴OE=ON+NE=+=7．‎ 点评：‎ 本题考查了圆的综合题：掌握切线的性质、圆周角定理及其推论；学会运用待定系数法求函数的解析式；熟练运用勾股定理和相似比进行几何计算．‎ ‎18、(2013浙江丽水)如图，在△ABC中，AB=AC，∠BAC=54°，以AB为直径的⊙O分别交AC，BC于点D，E，过点B作⊙O的切线，交AC的延长线于点F。‎ ‎（1）求证：BE=CE；‎ ‎（2）求∠CBF的度数；‎ ‎（3）若AB=6，求的长。‎ ‎19、（2013成都市）如图，的半径r=25,四边形ABCD内接于，于点H，P为CA延长线上的一点，且。‎ ‎ （1）试判断PD与的位置关系，并说明理由；‎ ‎ （2）若，,求BD的长；‎ ‎（3）在（2）的条件下，求四边形ABCD的面积。‎ 解析：‎ ‎（1）PD与⊙O相切，∠ABD=∠AOD ‎ ∠ADO+∠ADO=90° ∴∠ADO+∠PDA=90°‎ ‎∴PD⊥DO即PD与⊙O相切 ‎（2）设AH=x，AC⊥BD ∠PHD=90°‎ 由tan∠ADB=知DH=‎ 又PA= ∴PH=PA+AH=‎ ‎∴PD==2DH ⇒∠PDH=60°‎ 因为PD为⊙O切线，由割线弦定理知∠DCB=∠PDH=60°‎ ‎∴∠DOB=120° BD=2R·sin60°=2×25×=25‎ ‎（3）过A作AG⊥PD ‎∵PA= ∠DPH=30°‎ ‎∴GA= PG=‎ ‎∴tan∠PDA=‎ ‎∴‎ ‎∴ ‎ ‎∴‎ 又AC⊥BD ∴S=‎ ‎ ‎