湖北省黄石2010年中考数学试卷 7页

黄石市2010年初中毕业生学业考试 数学试题卷 姓名 考号 ‎ 注意事项：‎ ‎1. 本试卷分为试题卷和答题卷两部分。考试时间120分钟，满分120分。‎ ‎2.考生在答题前请阅读答题卷中的“注意事项”，然后按要求答题。‎ ‎3.所有答案均须做在答题卷相应区域，做在其它区域内无效。‎ 一、仔细选一选（本题有10个小题，每小题3分，共30分）‎ ‎1.已知－2的相反数是a，则a是（ ）‎ A.2 B.－ C. D. －2‎ ‎2.下列运算正确的是（ ）‎ A. ·= B. C. +＝2 D. ÷a＝‎ ‎3.已知x＜1，则化简的结果是（ ）‎ A.x－1 B. x＋1 C. －x－1 D.1－x ‎4. 不等式组的正整数解的个数是（ ） ‎ A.2个 B.3个 C.4个 D.5个 ‎5.下面既是轴对称又是中心对称的几何图形是（ ）‎ A.角 B.等腰三角形 C.平行四边形 D.正方形 ‎6.一个正方体的每个面都写有一个汉字，其平面展开图如图所示，则在该正方体中，和“崇”相对的面上写的汉字是（ ）‎ A.低 B.碳 C.生 D.活 ‎7.如图，直角梯形ABCD中，AD∥BC,∠ADC＝∠BAC＝90°,AB＝2,CD＝,则AD的长为（ ）‎ A. B.2 C.3 D. ‎ ‎8.如图，从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC，将剪下来的扇形围成一个圆锥，则圆锥的底面圆半径为（ ）‎ A. B. C. D. ‎ ‎9.同时投掷两个质地均匀的骰子，出现的点数之和为3的倍数的概率为（ ）‎ A. B. C. D. ‎ ‎10.如图，反比例函数（k＞0）与一次函数的图象相交于两点A(,),B(,),线段AB交y轴与C，当|－ |=2且AC = 2BC时，k、b的值分别为（ ）‎ A.k＝,b＝2 B.k＝,b＝1 C.k＝,b＝ D.k＝,b＝‎ 二、认真填一填（本题有6个小题，每小题3分，共18分）‎ ‎11.分解因式：4x2－9＝ .‎ ‎12.盒子中装有7个红球，2个黄球和1个蓝球，每个球除颜色外没有其它的区别，从中任意摸出一个球，这个球不是红球的概率为 .‎ ‎13. 如图，等腰三角形ABC中，已知AB＝AC，∠A＝30°，AB的垂直平分线交AC于D，则∠CBD的度数为 .‎ ‎14.如图，⊙O中，OA⊥BC,∠AOB＝60°,则sin∠ADC＝ .‎ ‎15.将函数y＝－6x的图象向上平移5个单位得直线，则直线与坐标轴围成的三角形面积为 .‎ ‎16.若自然数n使得作竖式加法n＋(n＋1)＋(n＋2)均不产生进位现象，则称n为“可连数”，例如32是“可连数”，因为32＋33＋34不产生进位现象；23不是“可连数”，因为23＋24＋25产生了进位现象，那么小于200的“可连数”的个数为 .‎ 三、全面答一答（本题9个小题，共72分）‎ ‎17.（本小题满分7分）计算：（2－）（2＋）＋－‎ ‎18.（本小题满分7分）先化简，再求值：÷.其中a＝＋1, b＝.‎ ‎19.（本小题满分7分）如图，正方形ABCD中，E、F分别是AB、BC边上的点，且AE＝BF，求证AF⊥DE.‎ ‎20.（本小题满分8分）解方程组：‎ ‎21.（本小题满分8分）某校今年有300名初中毕业生，毕业前该校进行了一次模拟考试.学校随即抽取了50名学生的数学成绩进行了分段统计（统计图表如下），已知数学试卷满分为120分，若规定得分率：低于60%为不及格；不小于80%为优秀；不小于90%为拔尖.‎ ⑴请结合扇形图和统计表填写图表中缺失的数据；‎ ⑵根据统计数据在所给的坐标系中画出直方图；‎ ⑶根据样本统计的有关数据，估计在整个毕业生中，大约有多少人不及格？优秀率约为多少？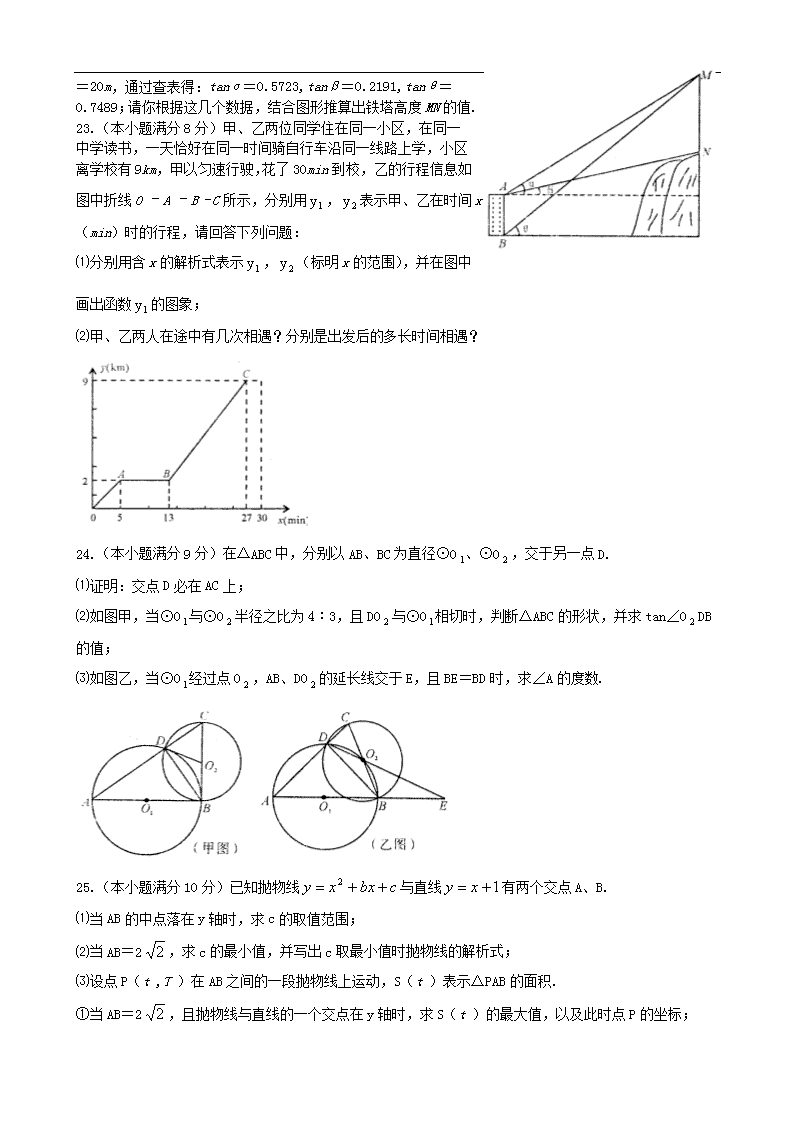‎ ‎22.（本小题满分8分）某乡镇中学教学楼对面是一座小山，去年“联通”公司在山顶上建了座通讯铁塔.甲、乙两位同学想测出铁塔的高度，他们用测角器作了如下操作：甲在教学楼顶A处测得塔尖M的仰角为α，塔座N的的仰角为β；乙在一楼B处只能望到塔尖M，测得仰角为θ（望不到底座），他们知道楼高AB ‎＝20m，通过查表得：tanα＝0.5723,tanβ＝0.2191,tanθ＝0.7489；请你根据这几个数据，结合图形推算出铁塔高度MN的值.‎ ‎23.（本小题满分8分）甲、乙两位同学住在同一小区，在同一中学读书，一天恰好在同一时间骑自行车沿同一线路上学，小区离学校有9km，甲以匀速行驶，花了30min到校，乙的行程信息如图中折线O –A –B -C所示，分别用，表示甲、乙在时间x（min）时的行程，请回答下列问题：‎ ⑴分别用含x的解析式表示，（标明x的范围），并在图中画出函数的图象；‎ ⑵甲、乙两人在途中有几次相遇？分别是出发后的多长时间相遇？‎ ‎24.（本小题满分9分）在△ABC中，分别以AB、BC为直径⊙O、⊙O，交于另一点D.‎ ⑴证明：交点D必在AC上；‎ ⑵如图甲，当⊙O与⊙O半径之比为4︰3，且DO与⊙O相切时，判断△ABC的形状，并求tan∠ODB的值；‎ ⑶如图乙，当⊙O经过点O，AB、DO的延长线交于E，且BE＝BD时，求∠A的度数.‎ ‎25.（本小题满分10分）已知抛物线与直线有两个交点A、B.‎ ⑴当AB的中点落在y轴时，求c的取值范围；‎ ⑵当AB＝2，求c的最小值，并写出c取最小值时抛物线的解析式；‎ ⑶设点P（t ,T ）在AB之间的一段抛物线上运动，S（t ）表示△PAB的面积.‎ ①当AB＝2，且抛物线与直线的一个交点在y轴时，求S（t ）的最大值，以及此时点P的坐标；‎ ②当AB＝m（正常数）时，S（t ）是否仍有最大值，若存在，求出S（t ）的最大值以及此时点P的坐标（t ,T ）满足的关系，若不存在说明理由.‎ 湖北省阳新县太子中学程正兴供稿