2012年鸡西中考数学试卷 12页

二○一二年鸡西市初中毕业学业考试 数 学 试 卷 本考场试卷序号 ‎（由监考教师填写）‎ 考生注意：‎ ‎1.考试时间120分钟 ‎2.全卷共三道大题，总分120分 ‎3.使用答题卡的考生，请将答案填写在答题卡的指定位置 题号 一 二 三 总 分 核分人 ‎21‎ ‎22‎ ‎23‎ ‎24‎ ‎25‎ ‎26‎ ‎27‎ ‎28‎ 得分 得分 评卷人 一、 单项选择题（每题3分，满分30分）‎ ‎1. 下列各式:① x2+x3=x5 ② a3·a2= a6 ③=-2 ④ =3 ⑤（π-1）0 =1，其中 正确的是 （ ）‎ A. ④⑤ B. ③④ C. ②③ D. ①④‎ ‎2. 下列图形既是轴对称图形，又是中心对称图形的是 （ ） ‎ ‎ A B C D D A C P F E B ‎3. 小亮为今年参加中考的好友小杰制作了一个正方体礼品盒（如图），六个面上各有一个字，连起来就是“预祝中考成功”，其中“预”的对面是“中”，“成”的对面是“功”，则它的平面展开图可能是 （ ） ‎ ‎ ‎ F E D C B A B C D ‎ 第4题图 ‎ ‎4. 如图，在△ABC中，BC=4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于点E，交AC于点F，点P是⊙A上的一点,且∠EPF=45°，则图中阴影部分的面积为 （ ） ‎ ‎ A.4-π B.4-2π C.8+π D.8-2π ‎ ‎5. 2012年5月份，鸡西地区一周空气质量报告中某项污染指数的数据是：31，35，30，31，34，32，31，这组数据的中位数、众数分别是 （ ）‎ A.32，31 B.31，‎31 ‎‎ C.31，32 D.32，35 ‎ S(米)‎ t（分）‎ O ‎18‎ ‎6. 一天晚饭后，小明陪妈妈从家里出去散步，下图描述了他们散步过程中离家的距离s（米）与散步时间t(分)之间的函数关系，下面的描述符合他们散步情景的是 （ ）‎ A.从家出发，到了一家书店，看了一会儿书就回家了 B.从家出发，到了一家书店，看了一会儿书，继续向 前走了一段，然后回家了 C.从家出发，一直散步（没有停留），然后回家了 D.从家出发，散了一会儿步，到了一家书店，看了一会儿书，‎ 继续向前走了一段，18分钟后开始返回 第6题图 ‎7. 为庆祝“六·一”国际儿童节，鸡冠区某小学组织师生共360人参加公园游园活动，有A、B两种型号客车可供租用，两种客车载客量分别为45人、30人，要求每辆车必须满载，则师生一次性全部到达公园的租车方案有 （ ） ‎ O ‎1‎ ‎3‎ A.3种 B.4种 C.5种 D.6种 ‎ ‎8. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，现有下列结论：‎ ‎ ① abc＞0 ② b2‎-4ac＜0 ③ ‎4a-2b+c＜0 ④b=‎‎-2a 则其中结论正确的是 （ ）‎ A. ①③ B. ③④ C. ②③ D. ①④‎ ‎9. 若关于的分式方程 =无解，则的值为（ ） 第8题图 ‎ A. -1.5 B. ‎1 ‎‎ C.－1.5或 2 D.－0.5或-1.5 ‎ ‎10.Rt△ABC中，AB=AC,点D为BC中点.∠MDN=90°，∠MDN绕点D旋转，‎ DM、DN分别与边AB、AC交于E、F两点.下列结论 ‎ A D F E N M B ‎①（BE+CF）=BC ② S△AEF≤S△ABC ③ S四边形AEDF=AD·EF ‎ ‎④ AD≥EF ⑤ AD与EF可能互相平分，其中正确结论的 C 个数是 （ ) ‎ A.1个 B.2个 C.3个 D.4个 第10题图 ‎ 得分 评卷人 二、填空题（每题3分，满分30分）‎ ‎11. ‎2012年5月8日，“最美教师”张丽莉为救学生身负重伤，张老师舍己救人的事迹受到全国人民的极大关注，在住院期间，共有691万人以不同方式向她表示问候和祝福，将691万人用科学记数法表示为 人.（结果保留两个有效数字）‎ ‎12. 函数y= + 中，自变量x的取值范围是 .‎ ‎13. 如图，已知AC=BD，要使△ABC≌△DCB，则只需添加一个 适当的条件是 .（填一个即可）‎ 第13 题图 ‎14. 已知一个口袋中装有7个只有颜色不同的球，其中3个白球，　　 ‎ ‎4个黑球，若往口袋中再放入x个白球和y个黑球，从口袋 ‎ 第15 题图 中随机取出一个白球的概率是，则y与x之间的函数关系 式为 .　　　　　‎ ‎15. 如图所示，沿DE折叠长方形ABCD的一边，使点C落在AB 边上的点F处，若AD=8，且△AFD的面积为60，则△DEC的 ‎ ‎ 面积为 . 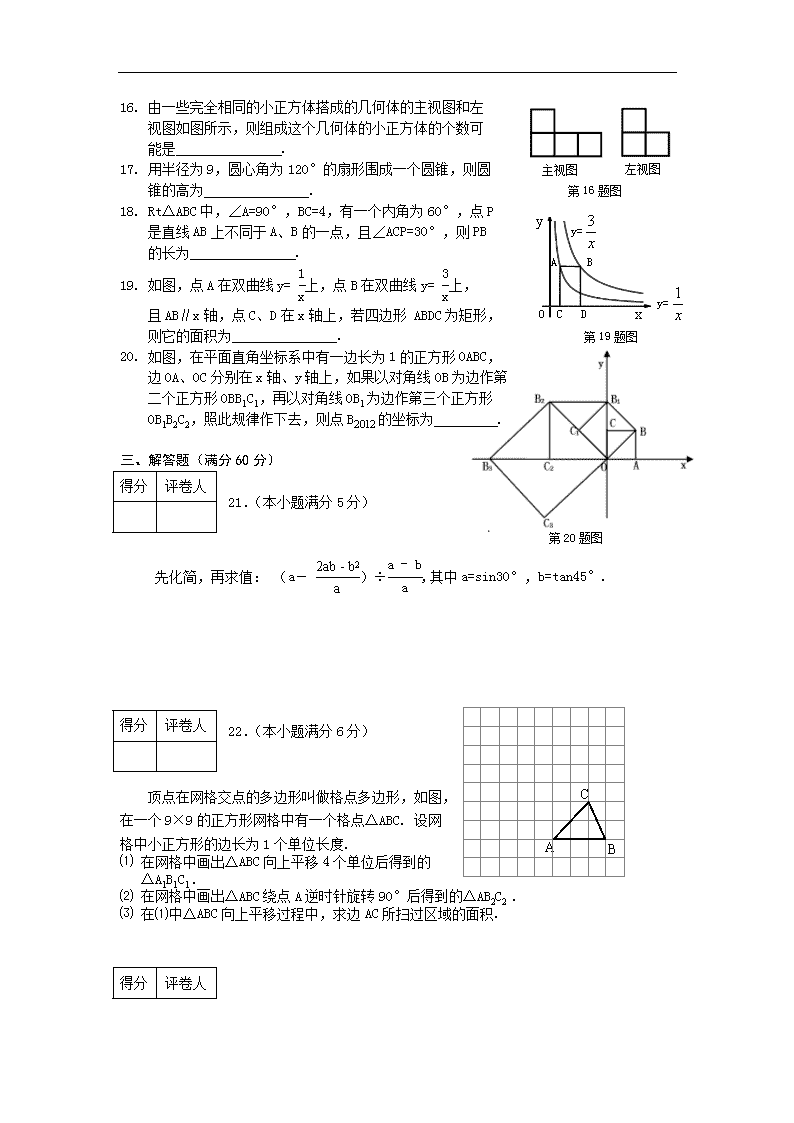‎ 主视图 左视图 ‎16. 由一些完全相同的小正方体搭成的几何体的主视图和左 视图如图所示，则组成这个几何体的小正方体的个数可 能是 . 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　‎ ‎17. 用半径为9，圆心角为120°的扇形围成一个圆锥，则圆 锥的高为 . 第16题图 A D y C x O y=‎ y=‎ ‎18. Rt△ABC中，∠A=90°，BC=4，有一个内角为60°，点P ‎ 是直线AB上不同于A、B的一点，且∠ACP=30°，则PB B 的长为 .‎ ‎19. 如图，点A在双曲线y= 上，点B在双曲线y= 上，‎ 且AB∥x轴，点C、D在x轴上，若四边形 ABDC为矩形，‎ 则它的面积为 . 第19题图 ‎20. 如图，在平面直角坐标系中有一边长为1的正方形OABC，‎ 边OA、OC分别在x轴、y轴上，如果以对角线OB为边作第 二个正方形OBB1C1，再以对角线OB1为边作第三个正方形 OB1B‎2C2，照此规律作下去，则点B2012的坐标为 .‎ 三、解答题（满分60分） ‎ 得分 评卷人 ‎21．（本小题满分5分）‎ 第20题图 ‎ ‎ 先化简，再求值： （a－ ）÷,其中a=sin30°，b=tan45°.‎ 得分 评卷人 A B C ‎22．（本小题满分6分） ‎ 顶点在网格交点的多边形叫做格点多边形，如图，‎ 在一个9×9的正方形网格中有一个格点△ABC. 设网 格中小正方形的边长为1个单位长度.‎ ‎⑴ 在网格中画出△ABC向上平移4个单位后得到的 ‎△A1B‎1C1 . ‎ ‎⑵ 在网格中画出△ABC绕点A逆时针旋转90°后得到的△AB‎2C2 .‎ ‎⑶ 在⑴中△ABC向上平移过程中，求边AC所扫过区域的面积.‎ 得分 评卷人 ‎23．（本小题满分6分）‎ 如图，抛物线=与x轴交于A、B两点，与y轴交于点C，且OA=2，OC=3.‎ (1) 求抛物线的解析式.‎ C y (2) 若点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标,若不存在,请说明理由. ‎ D ‎·‎ 注：二次函数（≠0）的对称轴是直线= - ‎ x A O B ‎ ‎ ‎ ‎ ‎ ‎ Ｘ ‎ ‎ ‎ ‎ 得分 评卷人 ‎24．（本小题满分7分）‎ ‎6月5日是世界环境日，为了普及环保知识，增强环保意识，某市第一中学举行了“环保知识竞赛”，参赛人数1000人，为了了解本次竞赛的成绩情况，学校团委从中抽取部分学生的成绩（满分为100分，得分取整数）进行统计，并绘制出不完整的频率分布表和不 完整的频数分布直方图如下：‎ ‎(1)直接写出a的值，并补全频数分布直方图.‎ ‎(2)若成绩在80分以上（含80分）为优秀，求这次参赛的学生中成绩为优秀的约为多少人？‎ ‎(3)若这组被抽查的学生成绩的中位数是80分，请直接写出被抽查的学生中得分为80分的至少有多少人？ ‎ 分 组 ‎ 频数 频率 ‎49.5～59.5‎ ‎0.08‎ ‎59.5～69.5‎ ‎0.12‎ ‎69.5～79.5‎ ‎20‎ ‎79.5～89.5‎ ‎32‎ ‎89.5～100.5‎ a ‎ ‎ ‎ ‎ ‎ ‎ 得分 评卷人 ‎25．（本小题满分8分）‎ S∕海里 黄岩岛是我国南沙群岛的一个小岛，渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后，发现一外国舰艇进入我国水域向黄岩岛驶来，渔船向渔政部门报告，并立即返航.渔政船接到报告后，立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的 距离s和渔船离开港口的时间t之间的函数图象.（假设渔船与渔政船沿同一航线航行）‎ ‎(1)直接写出渔船离港口的距离s和它离开港口的 时间t的函数关系式.‎ ‎13‎ ‎0‎ t(海里)‎ ‎5‎ t(海里)‎ ‎8‎ t(海里)‎ ‎150‎ t∕小时 t(海里)‎ ‎(2)求渔船和渔政船相遇时，两船与黄岩岛的距离.‎ ‎(3)在渔政船驶往黄岩岛的过程中，求渔船从港口 出发经过多长时间与渔政船相距‎30海里？‎ ‎ 　　　　　　　　　　　　　　　　　　‎ 得分 评卷人 ‎26．（本小题满分8分）‎ 如图1，在正方形ABCD中，点M、N分别在AD、CD上，若∠MBN=45°，易证MN=AM+CN ‎⑴ 如图2，在梯形ABCD中，BC∥AD，AB=BC=CD， 点M、N分别在AD、CD上，‎ A B C D M N 若∠MBN=∠ABC ,试探究线段MN、AM、CN有怎样的数量关系？请写出猜想，并给予证明．‎ ‎⑵ 如图3，在四边形ABCD中，AB=BC，∠ABC+∠ADC=180°，点M、‎ N分别在DA、CD的延长线上，若∠MBN=∠ABC，试探究线段 MN、AM、CN又有怎样的数量关系？请直接写出猜想，不需证明．‎ M D A A D M N C B C B ‎ N ‎ ‎ 图1 图2 图3‎ ‎ ‎ ‎ 第26题图 ‎ ‎ ‎ ‎ ‎ 得分 评卷人 ‎27．（本小题满分10分）‎ 为了迎接“五·一”小长假的购物高峰，某运动品牌服装专卖店准备购进甲、乙两种服装，甲种服装每件进价180元，售价320元；乙种服装每件进价150元，售价280元.‎ ‎⑴ 若该专卖店同时购进甲、乙两种服装共200件，恰好用去32400元，求购进甲、乙两种服装各多少件？‎ ‎⑵ 该专卖店为使甲、乙两种服装共200件的总利润（利润=售价-进价）不少于26700元，且不超过26800元，则该专卖店有几种进货方案？‎ ‎⑶ 在⑵的条件下，专卖店准备在5月1日当天对甲种服装进行优惠促销活动，决定对甲种服装每件优惠 a（0＜a＜20）元出售，乙种服装价格不变.那么该专卖店要获得最大利润应如何进货？‎ ‎ ‎ 得分 评卷人 ‎28．（本小题满分10分）‎ ‎ ‎ ‎ 如图，在平面直角坐标系中，已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上，并且OA、OB的长分别是方程x2－7x＋12=0的两根（OA＜OB），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动；‎ 同时，动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动，设点P、Q运动的时间为t秒. ‎ ‎（1）求A、B两点的坐标.‎ ‎（2）求当t为何值时，△APQ与△AOB相似，并直接写出此时点Q的坐标.‎ ‎（3）当t=2时，在坐标平面内，是否存在点M，使以A、P、Q、M为顶点的四边形是平行四边形？若存在，请直接写出M点的坐标；若不存在，请说明理由.‎ ‎ 　　　　　　 ‎ ‎ ‎ ‎ ‎ 第28题图 二○一二年鸡西市初中毕业学业考试 数学试题参考答案及评分说明 一、单项选择题（每题3分，满分30分）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ A D C A B D C B D C 二、填空题（每题3分，满分30分）‎ ‎11.6.9‎‎×106‎ ‎12.x＜1且x≠0‎ ‎13.AB=CD 或∠ACB=∠DBC等 ‎14. y=3x+5‎ ‎15. ‎ ‎16. 4或5或6或7（答对两值得1分，答对三值得2分，答对四值得3分）‎ ‎17. 6 ‎18. 或或4（答对一值得1分）‎ ‎19.2‎ ‎20.（－21006，－21006） 注：表示为（－（）2012，－（）2012）亦可 三、解答题（满分60分）‎ ‎21．（本小题满分5分）‎ 解：原式=· --------------------------------------------------------- (1分)‎ ‎﹦· -------------------------------------------------------- (1分)‎ ‎= --------------------------------------------------------- (1分)‎ 把=sin30°=，=tan45°=1代入 ------------------------------- (1分)‎ ‎ ‎ 原式=-1= - -------------------------------------------------- (1分)‎ A B C C1‎ B1‎ C2‎ A1‎ ‎22．（本小题满分6分）‎ ‎（1）平移正确给2分；‎ B2‎ ‎（2）旋转正确给2分；‎ ‎（3）扫过面积为8，正确给2分．‎ ‎23．（本小题满分6分）‎ 解：（1） 由已知条件得A（-2,0）， C（0,3） ----------------------------------- (1分)‎ ‎ ----------------------------------------------- (1分)‎ 解得 b= ， c= 3 ‎ ‎∴此二次函数的解析式为 y= - x2+x+3 ----------------------------------- ---- (1分)‎ ‎(2) 连接AD交对称轴于点P，则P为所求的点 ‎ 设直线AD解析式为y=kx+b ‎ 由已知得 -------------------------------------------------------- （1分）‎ ‎ 解得 k= ， b=1 ‎ ‎ ∴直线AD解析式为y=x+1 ------------------------------------------------------------ （1分）‎ 对称轴为直线 ：x= －= 当x = 时， y = ‎∴ P（，） ----------------------------------------------------------------------- （1分）‎ ‎24．（本小题满分7分）‎ 解：（1） a=0.28 ----------------------------------------------------------（1分）‎ 补全直方图 -----------------------------------------------------------------（2分）‎ ‎（2） 成绩优秀的学生约为：×1000=600（人） --------------------（2分）‎ ‎（3） 至少有11人 ---------------------------------------------------------（2分）‎ ‎25．（本小题满分8分）‎ 解：（1） 当0≤t≤5时 s =30t -----------------------------------------------------（1分）‎ 当5＜t≤8时 s=150 ----------------------------------------（1分）‎ 当8＜t≤13时 s=－30t+390 ------------------------------------（1分）‎ ‎（2） 渔政船离港口的距离与渔船离开港口的时间的函数关系式设为s=kt+b ‎ ‎ -----------------------------------------------------（1分）‎ 解得： k=45 b=－360‎ ‎∴s=45t－360 -----------------------------------------------------（1分）‎ 解得 t=10 s=90 ‎ 渔船离黄岩岛距离为 150－90=60 （海里） ------------------------（1分）‎ ‎(3) S渔=－30t+390‎ S渔政=45t－360‎ 分两种情况： ‎ ① S渔－S渔政=30 ‎ ‎－30t+390－（45t－360）=30‎ 解得t=（或9.6） ----------------------------------------------------（1分）‎ ② S渔政－S渔=30‎ ‎45t－360－（－30t+390）=30‎ 解得 t=（或10.4）‎ ‎∴当渔船离开港口9.6小时或10.4小时时， 两船相距‎30海里. -------（1分）‎ ‎26. （本小题满分8分）‎ 解：（1） 图2， 猜想：MN=AM+CN ---------------------------------------------（2分） ‎ ‎ 证明: 延长 NC至点F ，使 CF= AM，连接BF A B C D M N F ‎1‎ ‎2‎ ‎3‎ ‎ ∵四边形ABCD是等腰梯形 ‎ ∴∠DAB=∠ADC ‎ ‎ 又∵AD∥CB ‎ ‎ ∴∠ADC =∠BCF ‎ ∴∠BCF=∠DAB ‎ 又∵AB=BC AM=CF ‎ ‎ ∴△AMB≌△CFB --------------------------------------------（2分） ‎ ‎ ∴∠2=∠3 BM=BF ‎∵∠MBN=∠ABC ‎∴∠1+∠2=∠MBN ‎∴∠1+∠3=∠MBN 即∠MBN=∠NBF 又∵BN=BN BM=BF ‎ ∴△MBN≌△FBN ‎ ∴ MN=NF ‎ ∵NF=NC+CF ‎ ∴MN=AM+CN --------------------------------------------（2分）‎ ‎ （2）图3 猜想：MN=CN-AM ---------------------------------------------------（2分） ‎ ‎27．（本小题满分10分）‎ 解：（1） 设购进甲种服装x件，则购进乙种服装（200 －x）件 ‎ 180x+150（200 －x）=32400 ---------------------------------------------（1分） ‎ 解得 x=80 ------------------------------------------------- （1分）‎ ‎ ∴购进甲种服装80件，购进乙种服装120件. --------------------- （1分）‎ ‎ （2） 设购进甲种服装y件，则购进乙种服装（200 －y）件，根据题意得 ‎ 26700≤（320－180）y+（280－150）（200 －y）≤26800 ------ （2分）‎ ‎ 解得 70≤y≤80 ---------------------------------------------（1分） ‎ ‎ ∵y为正整数 ‎ ∴共有11种方案 ---------------------------------------------（1分） ‎ ‎ （3）设总利润为W元 W =（140－a）y+130（200－y）‎ ‎ =（10－a）y+26000‎ ‎①当0＜a＜10时，10－a＞0，W随y增大而增大，‎ ‎∴当y=80时，W有最大值，即此时购进甲种服装80件，‎ 乙种服装120件； --------------------------------------------（1分） ‎ ‎②当a=10时，（2）中所有方案获利相同，‎ 所以按哪种方案进货都可以； ---------------------------------------------（1分）‎ ‎ ③当10＜a＜20时，10－a＜0 ，W随y增大而减小，当y=70时，‎ W有最大值，即此时购进甲种服装70件，‎ 乙种服装130件. --------------------------------------------（1分）‎ ‎28．（本小题满分10分）‎ 解：（1）x2－7 x +12=0‎ ‎ 解得x1=3，x2=4 ----------------------------------------------------（1分）‎ ‎ ∵OA＜OB ‎ ‎ ∴OA=3 , OB=4‎ ‎ ∴A(0,3) , B(4,0) --------------------------------------------------（2分）‎ ‎ ‎ 图1 图2‎ (2) 由题意得，AP=t, AQ=5-2t ‎ 可分两种情况讨论：‎ ① 当∠APQ=∠AOB 时，△APQ∽△AOB 如图1 = ‎ 解得 t= --------------------------------------------------（1分） ‎ ‎ 所以可得 Q（，）--------------------------------------------------（1分）‎ ② ‎ 当 ∠AQP=∠AOB 时， △APQ∽△ABO ‎ 如图2 = ‎ 解得 t= --------------------------------------------------（1分）‎ ‎ 所以可得 Q（，）--------------------------------------------------（1分）‎ ‎（3） 存在 M1（，）， M2（，），M3（－，）---------------（3分）‎ 说明：以上各题，如果有其它正确解法，可酌情给分.‎