中考数学第29圆的有关性质一轮复习学案 4页

第29课时 圆的有关性质 ‎ 一、考试大纲要求：‎ ‎1、理解圆及其有关概念，了解弧、弦、圆心角的关系，探索并了解点与圆的位置关系。‎ ‎2、探索圆的性质，了解圆周角与圆心角的关系、直径所对圆周角的特征。‎ ‎3、了解三角形的外心 二、重点、易错点分析：‎ ‎1．重点：垂径定理，弧、弦、圆心角的关系 ‎2．易错点难点：辅助线的添加 三、考题集锦：‎ ‎1．选择题 ‎1、（2011上海6题）矩形ABCD中，AB＝8，，点P在边AB上，且BP＝3AP，如果圆P是以点P为圆心，PD为半径的圆,那么下列判断正确的是（ ).‎ ‎(A) 点B、C均在圆P外； (B) 点B在圆P外、点C在圆P内；‎ ‎(C) 点B在圆P内、点C在圆P外； (D) 点B、C均在圆P内．‎ ‎2、（2012山东泰安，11，3分）如图，AB是⊙的直径，弦CD⊥AB，垂足为M，下列结论不成立的是（ ）‎ A.CM=DM B. 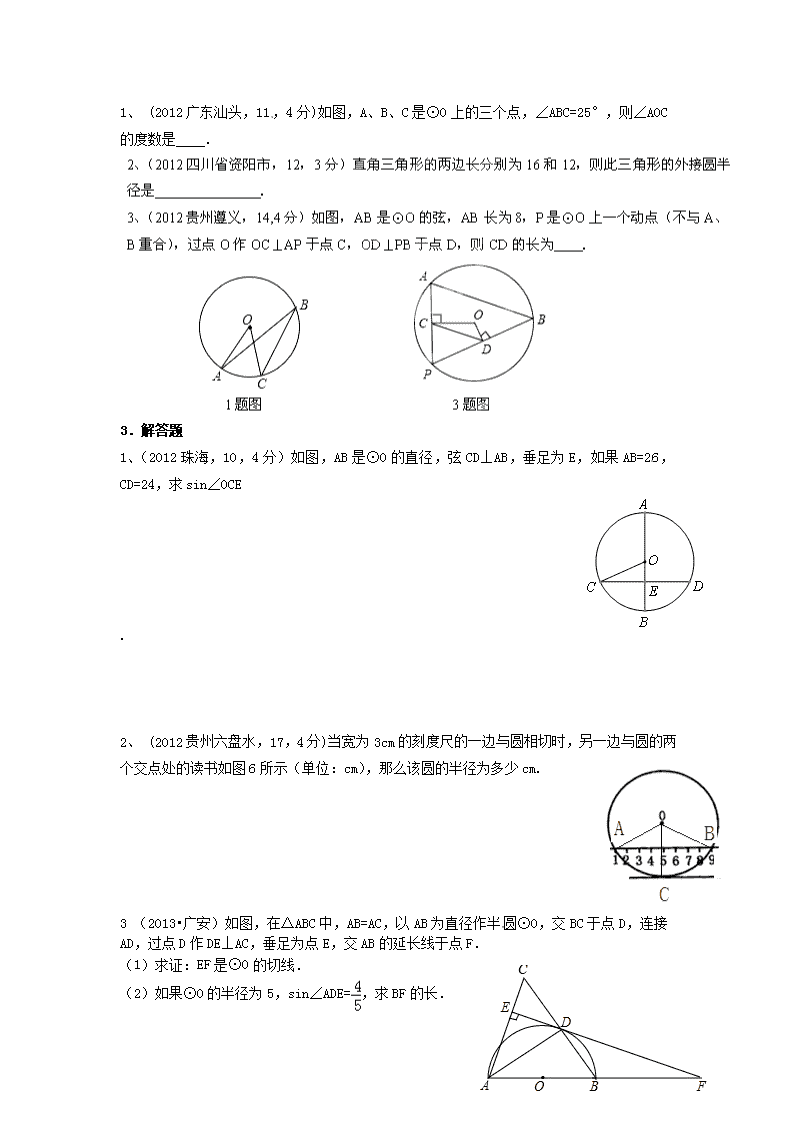C.∠ACD=∠ADC D.OM=MD 谢勇 ‎ 2题图 3题图 4题图 ‎3、（2012湖北随州，7,3分）如图，AB是⊙O的直径，若∠BAC=35°，则∠ADC=( )‎ A．35° B．55° C．70° D．110°‎ ‎4、(2012江苏苏州，5，3分)如图，已知BD是⊙O的直径，点A、C在⊙O上，=，∠AOB=60°，则∠BDC的度数是（　　）‎ A．20° B．25° C．30° D．40°‎ ‎2．填空题 ‎1、 (2012广东汕头，11，4分)如图，A、B、C是⊙O上的三个点，∠ABC=25°，则∠AOC的度数是　　．‎ ‎3．解答题 ‎1、（2012珠海，10，4分）如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=26，CD=24，求sin∠OCE ‎.‎ ‎2、 (2012贵州六盘水，17，4分)当宽为‎3cm的刻度尺的一边与圆相切时，另一边与圆的两个交点处的读书如图6所示（单位：cm），那么该圆的半径为多少cm.‎ ‎3 （2013•广安）如图，在△ABC中，AB=AC，以AB为直径作半圆⊙0，交BC于点D，连接AD，过点D作DE⊥AC，垂足为点E，交AB的延长线于点F．‎ ‎（1）求证：EF是⊙0的切线．‎ ‎（2）如果⊙0的半径为5，sin∠ADE=，求BF的长．‎ 四、典型例题：‎ 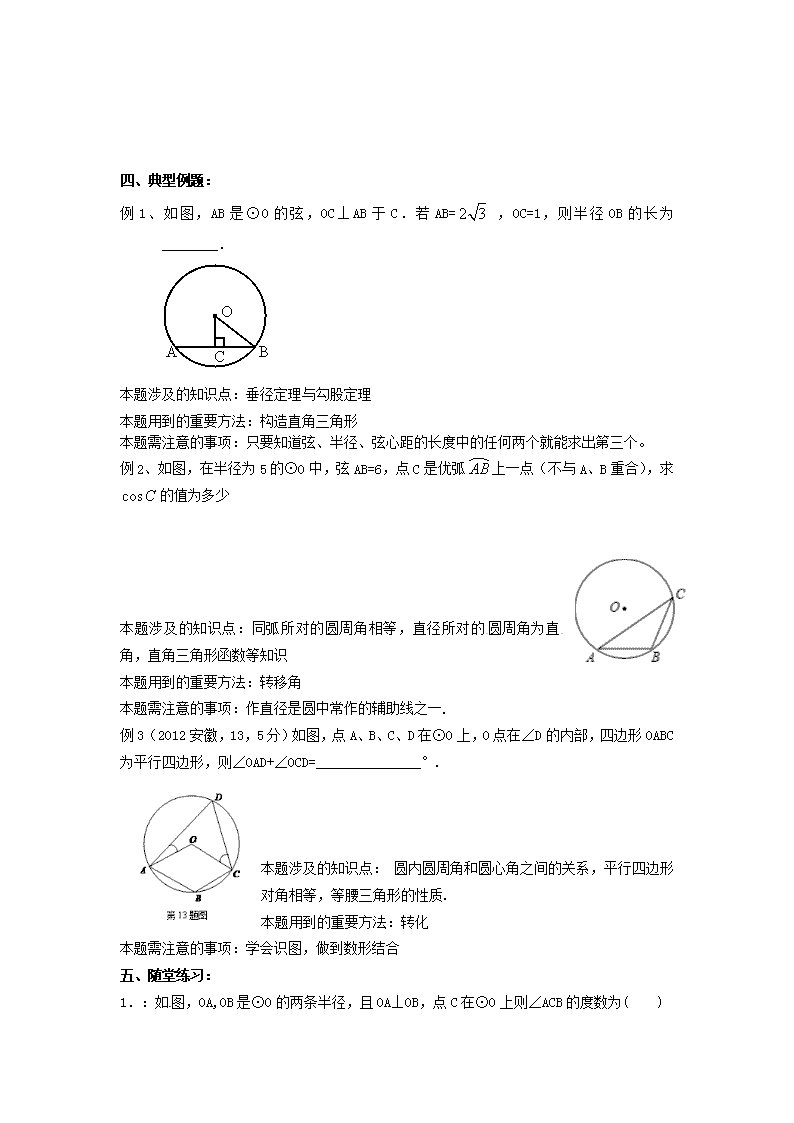例1、如图，AB是⊙O的弦，OC⊥AB于C．若AB= ，0C=1，则半径OB的长为________．‎ 本题涉及的知识点：垂径定理与勾股定理 本题用到的重要方法：构造直角三角形 本题需注意的事项：只要知道弦、半径、弦心距的长度中的任何两个就能求出第三个。‎ 例2、如图，在半径为5的⊙O中，弦AB=6，点C是优弧上一点（不与A、B重合），求的值为多少 ‎ 本题涉及的知识点：同弧所对的圆周角相等，直径所对的圆周角为直角，直角三角形函数等知识 本题用到的重要方法：转移角 本题需注意的事项：作直径是圆中常作的辅助线之一.‎ 例3（2012安徽，13，5分）如图，点A、B、C、D在⊙O上，O点在∠D的内部，四边形OABC为平行四边形，则∠OAD+∠OCD=_______________°.‎ 本题涉及的知识点： 圆内圆周角和圆心角之间的关系，平行四边形对角相等，等腰三角形的性质.‎ 本题用到的重要方法：转化 本题需注意的事项：学会识图，做到数形结合 五、随堂练习：‎ ‎1．：如图，OA,OB是⊙O的两条半径，且OA⊥OB，点C在⊙O上则∠ACB的度数为( )‎ A.45° B.35° C.25° D.20°‎ ‎2．已知AB、CD是⊙O的两条直径，∠ABC=30°，那么∠BAD=‎ 图2‎ A.45° B. 60° C.90° D. 30°‎ 六、本课小结：‎ ‎1．知识：点与圆的位置关系 垂径定理 弧、弦、圆心角、圆周角之间的关系 ‎2．方法：转化构造直角三角形 ① 作垂径 ② 直径所对的圆周角是直角 ‎3．注意事项：圆和其他知识结合的较多，注意发现其中的信息 ‎4．发现问题：计算要准确