中考数学压轴题3 8页

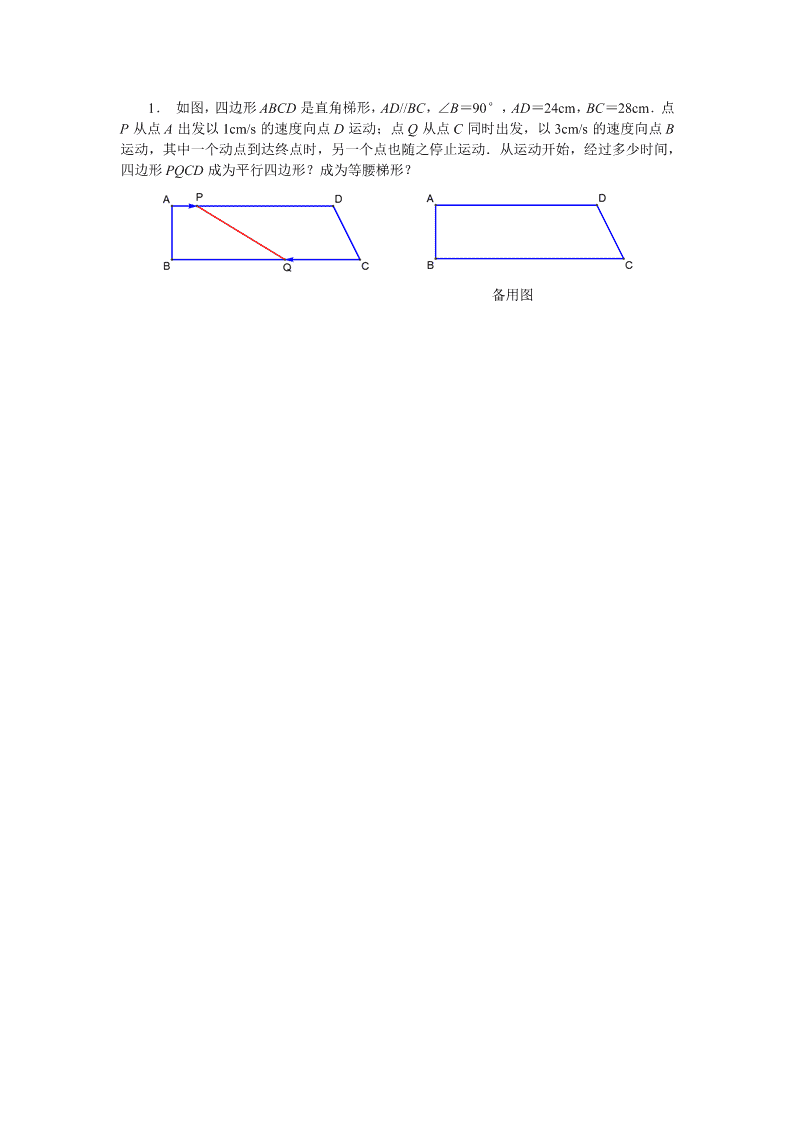
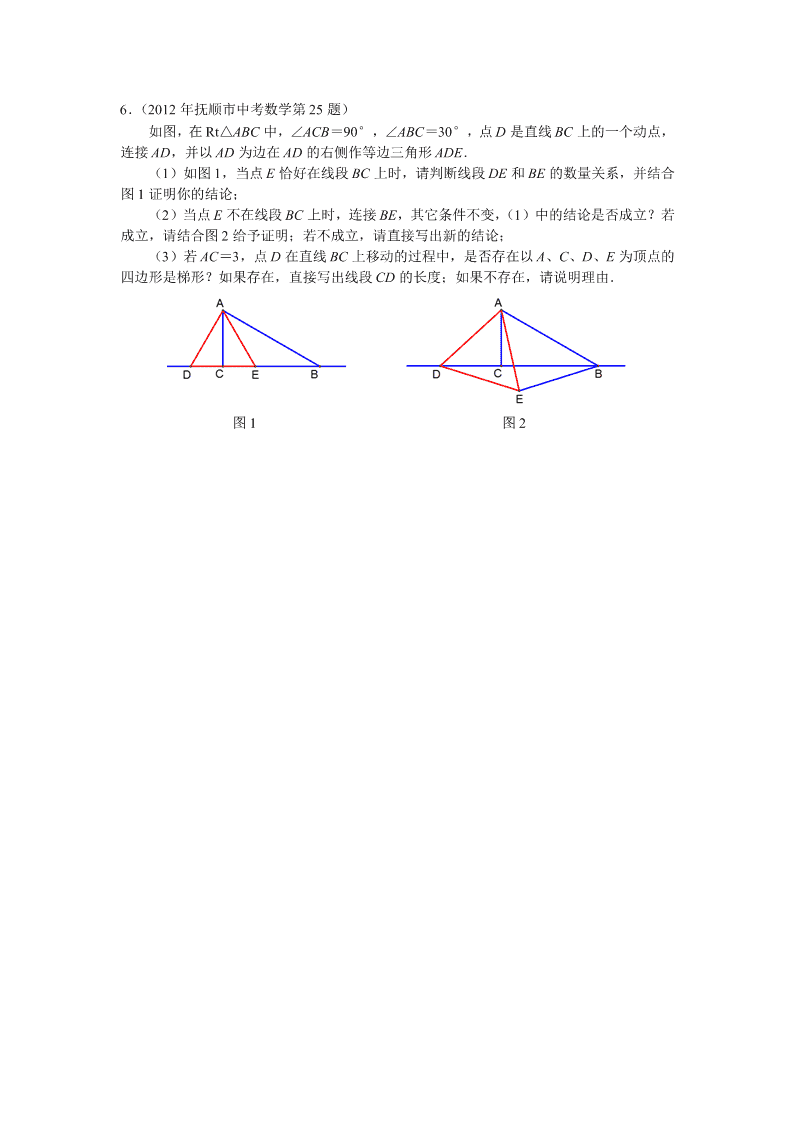
1． 如图，四边形 ABCD 是直角梯形，AD//BC，∠ B＝90°，AD＝24cm，BC＝28cm．点 P 从点 A 出发以 1cm/s 的速度向点 D 运动；点 Q 从点 C 同时出发，以 3cm/s 的速度向点 B 运动，其中一个动点到达终点时，另一个点也随之停止运动．从运动开始，经过多少时间， 四边形 PQCD 成为平行四边形？成为等腰梯形？ 备用图 1．如图 1，如果四边形 PQCD 是平行四边形，那么 PD＝QC． 所以 24－t＝3t．解得 t＝6． 如图 2，如果四边形 PQCD 是等腰梯形，作 PM⊥BC，DN⊥BC，垂足分别为 M、N， 那么 QM＝CN． 所以 t－(28－3t)＝4．解得 t＝8． 第 1 题图 1 第 1 题图 2 6．（ 2012 年抚顺市中考数学第 25 题） 如图，在 Rt△ABC 中，∠ACB＝90°，∠ABC＝30°，点 D 是直线 BC 上的一个动点， 连接 AD，并以 AD 为边在 AD 的右侧作等边三角形 ADE． （1）如图 1，当点 E 恰好在线段 BC 上时，请判断线段 DE 和 BE 的数量关系，并结合 图 1 证明你的结论； （2）当点 E 不在线段 BC 上时，连接 BE，其它条件不变，（1）中的结论是否成立？若 成立，请结合图 2 给予证明；若不成立，请直接写出新的结论； （3）若 AC＝3，点 D 在直线 BC 上移动的过程中，是否存在以 A、C、D、E 为顶点的 四边形是梯形？如果存在，直接写出线段 CD 的长度；如果不存在，请说明理由． 图 1 图 2 6．（1）当点 E 恰好在线段 BC 上时，由∠ADE＝60°，∠ABC＝30°， 得∠DAB＝90°．因此∠EAB＝30°．所以 AE＝BE．所以 DE＝BE． （2）如图 1，延长 AC 至 F，使得 CF＝AC，那么△ABF 是等边三角形． 联结 DF．由于 BD 垂直平分 AF，所以 DA＝DF． 由 AD＝AC，∠DAF＝∠EAB，AF＝AB，得△ADF≌△AEB．所以 DF＝EB． 由于 DE＝DA，所以 DE＝BE． （3）①如图 2，当 AE//CD 时，∠ADC＝∠DAE＝60°． 在 Rt△ACD 中，AC＝3，所以 CD＝ 3 ． ②如图 3，当 AC//ED 时，∠CAD＝∠ADE＝60°．此时 D、B 重合，CD＝3 ． 第 6 题图 1 第 6 题图 2 第 6 题图 3 两年模拟 9．（ 2014 年上海市闸北区中考模拟第 24 题） 如图，二次函数 y＝ax2＋4 的图像与 x 轴交于点 A 和点 B（点 A 在点 B 的左侧），与 y 轴交于点 C，且 cos∠CAO＝ 2 2 ． （1）求二次函数的解析式； （2）若以点 O 为圆心的圆与直线 AC 相切于点 D，求点 D 的坐标； （3）在（2）的条件下，抛物线上是否存在点 P 使得以 P、A、D、O 为顶点的四边形 是直角梯形．．．．，若存在，请求出点 P 坐标；若不存在，请说明理由． 图 1 9.（1）由 y＝ax2＋4，得 C(0, 4)．所以 OC＝4． 由 cos∠CAO＝ 2 2 ，得∠CAO＝45°．所以 OA＝4，A(－4, 0)． 将 A(－4, 0)代入 y＝ax2＋4，得 16a＋4＝0．解得 1 4a  ． 所以二次函数的解析式是 21 44yx   ． （2）如图 1，由 A(－4, 0)、C(0, 4)， 可知直线 AC 与坐标轴的夹角为 45°． 当⊙O 与 AC 相切于点 D 时，OD⊥AC， 所以 D 是 AC 的中点，D(－2, 2)． 第 9 题图 1 （3）设点 P 的坐标为 21( , 4)4xx． 因为∠ADO＝90°，因此直角梯形存在两种情况： 如图 2，当 AP//DO 时，点 P 在第四象限，作 PH⊥x 轴，那么 PH＝AH． 解方程 21( 4) 44 xx     ，得 x＝8，或 x＝－4（与 A 重合，舍去）． 此时点 P 的坐标为(8, －12)． 如图 3，当 OP//DA 时，点 P 在第三象限，作 PH⊥x 轴，那么 PH＝OH． 解方程 21( 4)4 xx     ，得 2 2 5x    ，或 2 2 5x    （舍去）． 此时点 P 的坐标为( 2 2 5, 2 2 5)    ． 第 9 题图 2 第 9 题图 3 10．（ 2014 年上海市闵行区中考模拟第 24 题） 如图，把两个全等的 Rt△AOB 和 Rt△COD 分别置于平面直角坐标系中，使直角边 OB、 OD 在 x 轴上．已知点 A(1，2)，过 A、C 两点的直线分别交 x 轴、y 轴于点 E、F．抛物线 y ＝ax2＋bx＋c 经过 O、A、C 三点． （1）求该抛物线的函数解析式； （2）点 P 为线段 OC 上的一个动点，过点 P 作 y 轴的平行线交抛物线于点 M，交 x 轴 于点 N，问是否存在这样的点 P，使得四边形 ABPM 为等腰梯形？若存在，求出此时点 P 的坐标；若不存在，请说明理由． 10．（1）将 A(1，2)、O(0，0)、C(2，1)分别代入 y＝ax2＋bx＋c， 得 2, 0, 4 2 1. abc c a b c          解得 3 2a  ， 7 2b  ， 0c  ． 所以 237 22y x x   ． （2）如图 1，过点 P、M 分别作梯形 ABPM 的高 PP′、MM′，如果梯形 ABPM 是等腰 梯形，那么 AM′＝BP′，因此 yA－yM′＝yP′－yB． 直线 OC 的解析式为 1 2yx ，设点 P 的坐标为 1( , )2xx，那么 237( , )22M x x x． 解方程 23 7 12 ( )2 2 2x x x    ，得 1 2 3x  ， 2 2x  ． x＝2 的几何意义是 P 与 C 重合，此时梯形不存在．所以 21( , )33P ． 第 10 题图 1