2019届中考数学一轮复习 第26课时 与圆有关的概念及性质导学案（无答案） 5页

第26课时 与圆有关的概念及性质 姓名 学号 班级 ‎ 学习目标 ‎1.理解圆、弧、弦、圆心角、圆周角的概念，了解等圆、等弧的概念．‎ ‎2.探索并掌握垂径定理及其推论．‎ ‎3.探索圆周角与圆心角及其所对弧的关系，了解并证明圆周角定理及其推论．‎ ‎4. 知道三角形的外心，并能画任意三角形的外接圆．‎ 学习重难点：利用圆周角与圆心角及其所对弧的关系 学习过程 一．知识梳理 ‎(1)圆的基本概念：‎ 在同一平面内，线段OA绕它固定的一个端点 形成的图形叫做圆， 叫做圆心， 叫做半径．圆上任意两点间的 叫做圆弧；在同圆或等圆中，能够 的弧叫做等弧．‎ ‎(2) 圆的有关性质：‎ ‎①对称性：圆是中心对称图形， 是它的对称中心；圆也是轴对称图形， 都是它的对称轴．‎ ‎②圆心角、弧、弦之间的关系：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别 .‎ ‎③垂径定理：垂直于弦的直径 弦，并且平分弦所对的两条弧．推论：平分弦(不是直径)的直径 于弦，并且平分这条弦所对的两条弧．‎ ‎⑶圆心角和圆周角：‎ ‎①圆心角：顶点在 的角叫做圆心角；圆心角的度数 它所对的弧的度数．圆周角：顶点在圆上，两边都与圆 的角叫做圆周角．‎ ‎②圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角 ，都等于这条弧所对的圆心角的 ．推论：半圆(或直径)所对的圆周角是 ，90°的圆周角所对的弦是 ．‎ ‎⑷确定圆的条件：‎ ‎①不在 的三个点可以确定一个圆．‎ ‎② 三角形的三个顶点确定一个圆，这个圆叫做三角形的外接圆．外接圆的圆心叫做三角形的 .‎ ‎⑸圆的内接四边形：圆的内接四边形的对角 .‎ 二、典型例题 ‎1.垂直定理及其推论 问题1.(2017·呼和浩特)如图，为的直径，弦，‎ 垂足为，若，，则的周长为 ( )‎ 5‎ A. B. C. D. ‎ ‎2.圆心角的应用 问题2 (2016·兰州)如图，在中，是的中点，，‎ 则的度数为 ( )‎ A. B. C. 　　D. ‎ ‎3.圆周角定理及其推论 问题3、点是△的外心，若，求的度数．‎ ‎4.圆内接四边形 问题4、(2017·广东)如图，四边形内接于，，，则的度数为( )‎ A. 　　 B. C. 　　 D. 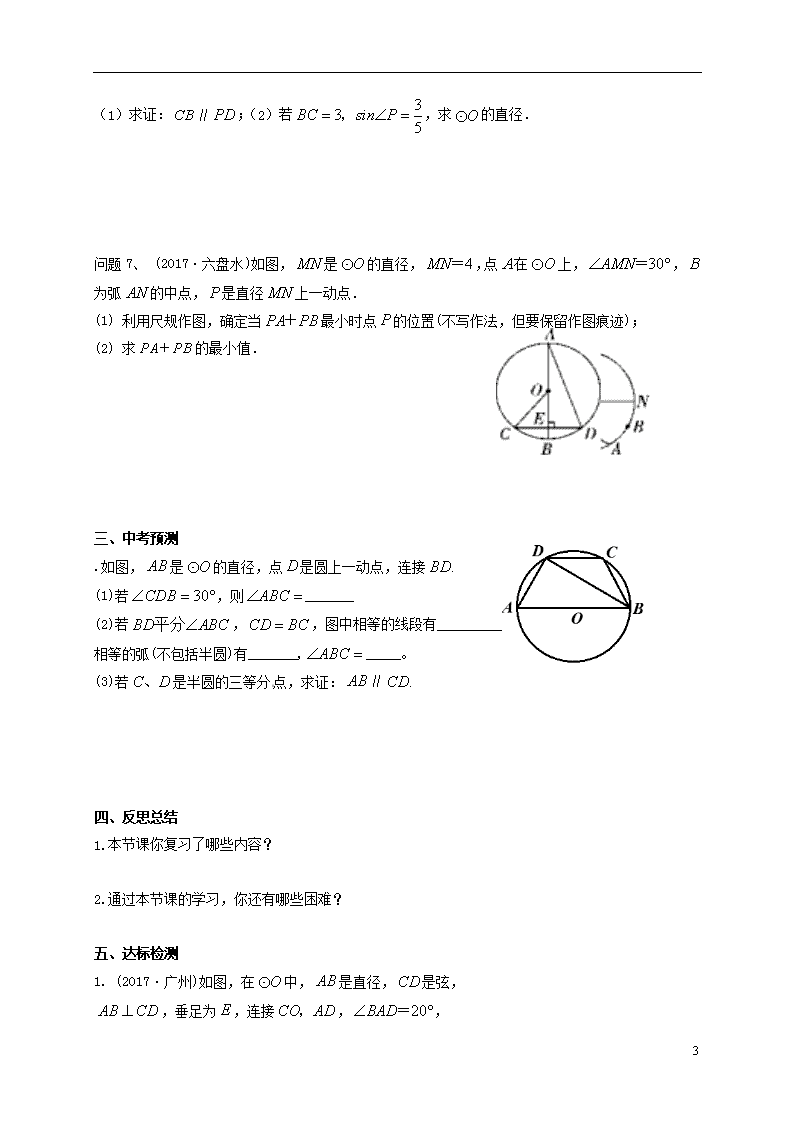‎ 问题5、如图，将沿弦折叠，圆弧恰好经过圆心，点是优弧上一点，‎ 求．‎ ‎5.圆的性质与其他知识的综合应用 问题6、（中考指要例3）如图，是的直径，弦与点，点在上，，‎ 5‎ ‎（1）求证：∥；（2）若，求的直径．‎ 问题7、 (2017·六盘水)如图，是的直径，，点在上，，为弧的中点，是直径上一动点．‎ ‎(1) 利用尺规作图，确定当最小时点的位置(不写作法，但要保留作图痕迹)；‎ ‎(2) 求的最小值．‎ 三、中考预测 ‎.如图，是的直径，点是圆上一动点，连接 ‎(1)若，则_______‎ ‎(2)若，，图中相等的线段有__________，‎ 相等的弧(不包括半圆)有_______,_____。‎ ‎(3)若是半圆的三等分点，求证：∥‎ 四、反思总结 ‎1.本节课你复习了哪些内容？‎ ‎2.通过本节课的学习，你还有哪些困难？‎ 五、达标检测 ‎1. (2017·广州)如图，在中，是直径，是弦，‎ ‎，垂足为，连接，，‎ 5‎ 则下列说法正确的是 ( )‎ A. B. ‎ C. D. ‎ ‎2. (2017·衡阳)如图，点都在上，‎ 且点在弦所对的优弧上，如果，‎ 那么的度数是 ( )‎ A.26°　　 B. 30° C. 32°　　 D. 64°‎ ‎3. (2017·西宁)如图，是⊙O的直径，弦交 于点，，，，‎ 则的长为 ( )‎ ‎ A. B‎.2‎ C. D.8‎ ‎4. (2017·潍坊)点为半径是的圆周上两点，为的中点，以线段为邻边作菱形，顶点恰在该圆直径的三等分点上，则该菱形的边长为 ( )‎ A. 或 B.或‎2‎ C.或 D.或 ‎ ‎ ‎5. (2017·大连)如图，在中，弦，‎ 垂足为，则的半径为 ‎ ‎6. (2017·盐城)如图，将沿弦折叠，点在上，点在上，若，则 .‎ ‎7. (2017·北京)如图，为的直径，为上的点， ，若，则 .‎ ‎8. (2017·凉山州)如图，四边形内接于半径为的⊙O中，且，则 .‎ 5‎ ‎9. (2017·牡丹江)如图，在中，，于点，于点.‎ 求证：‎ ‎10．如图，在平行四边形中，，，点是边上的动点，以为半径的圆与边交于点 (点在点的右侧)，射线与射线交于点.(1)当圆经过点时，求的长；(2)连结，当∥时，‎ 求弦的长．‎ 5‎