中考数学总复习中档题集锦 11页

‎2013年中考数学总复习中档题集锦 ‎1．如图，△ABC中，AB=AC，∠BAC=90°，D、E是BC上的两点，且∠DAE=45°．将△AEC绕着点A顺时针旋转90°后，得到△AFB，连接DF．‎ ‎（1）请猜想DF与DE之间有何数量关系？‎ ‎（2）证明你猜想的结论．‎ ‎2．如图，已知抛物线y=x2+bx+c经过A（1，0），B（0，2）两点，顶点为D．将△OAB绕点A顺时针旋转90°后，点B落到点C的位置，将抛物线沿y轴平移后经过点C，求平移后所得图象的函数关系式．‎ ‎3．已知：如图，△ABC内接于⊙O，AB为直径，弦CF⊥AB于E，C是的中点，连接BD，连接AD，分别交CE、BC于点P、Q．‎ ‎（1）求证：P是AQ的中点；‎ ‎（2）若tan∠ABC=，CF=8，求CQ的长．‎ ‎4．已知：如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作DF⊥AC于点F，交BA的延长线于点E．‎ 求证：（1）BD=CD；‎ ‎（2）DE是⊙O的切线．‎ ‎5．如图，在△ABC中，D是BC边的中点，E、F分别在AD及其延长线上，CE∥BF，连接BE、CF．‎ ‎（1）求证：△BDF≌△CDE；‎ ‎（2）若AB=AC，求证：四边形BFCE是菱形．‎ ‎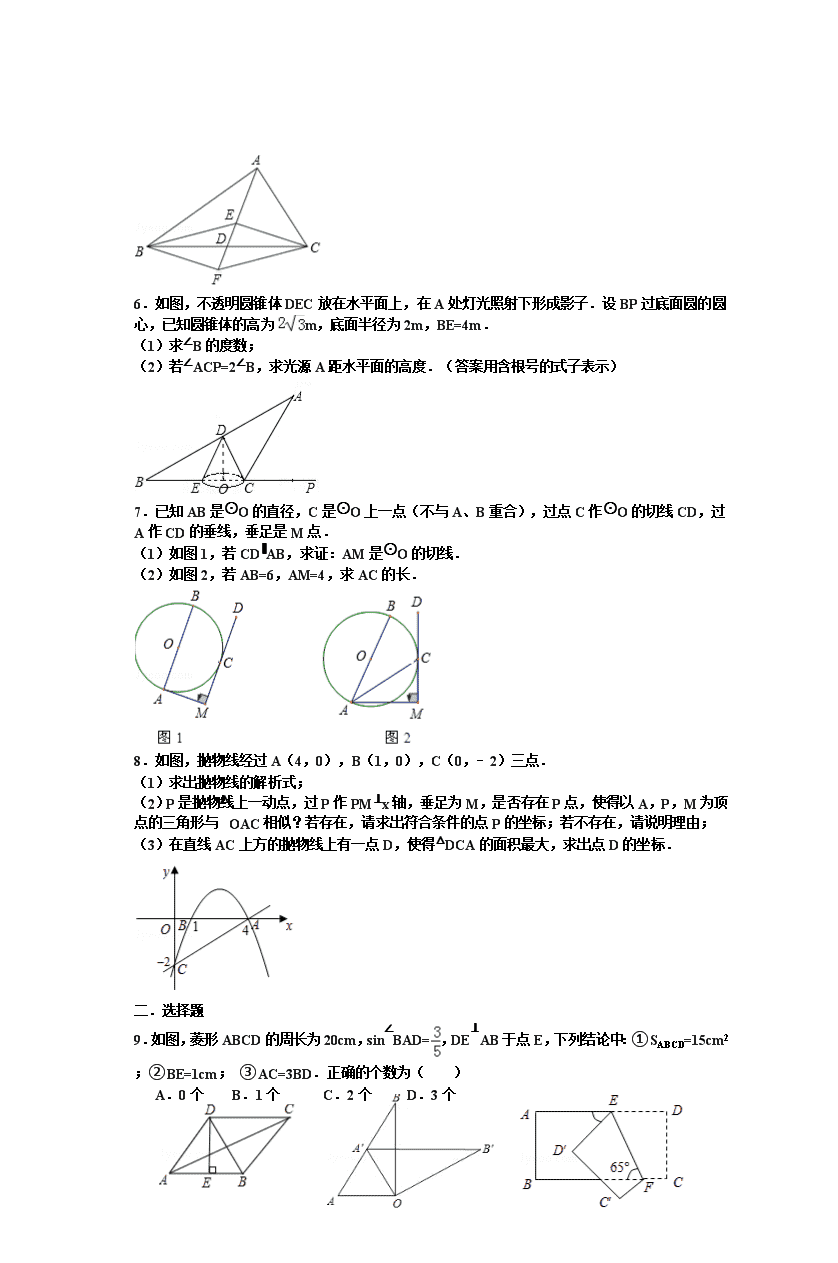6．如图，不透明圆锥体DEC放在水平面上，在A处灯光照射下形成影子．设BP过底面圆的圆心，已知圆锥体的高为m，底面半径为‎2m，BE=‎4m．‎ ‎（1）求∠B的度数；‎ ‎（2）若∠ACP=2∠B，求光源A距水平面的高度．（答案用含根号的式子表示）‎ ‎7．已知AB是⊙O的直径，C是⊙O上一点（不与A、B重合），过点C作⊙O的切线CD，过A作CD的垂线，垂足是M点．‎ ‎（1）如图1，若CD∥AB，求证：AM是⊙O的切线．‎ ‎（2）如图2，若AB=6，AM=4，求AC的长．‎ ‎8．如图，抛物线经过A（4，0），B（1，0），C（0，﹣2）三点．‎ ‎（1）求出抛物线的解析式；‎ ‎（2）P是抛物线上一动点，过P作PM⊥x轴，垂足为M，是否存在P点，使得以A，P，M为顶点的三角形与△OAC相似？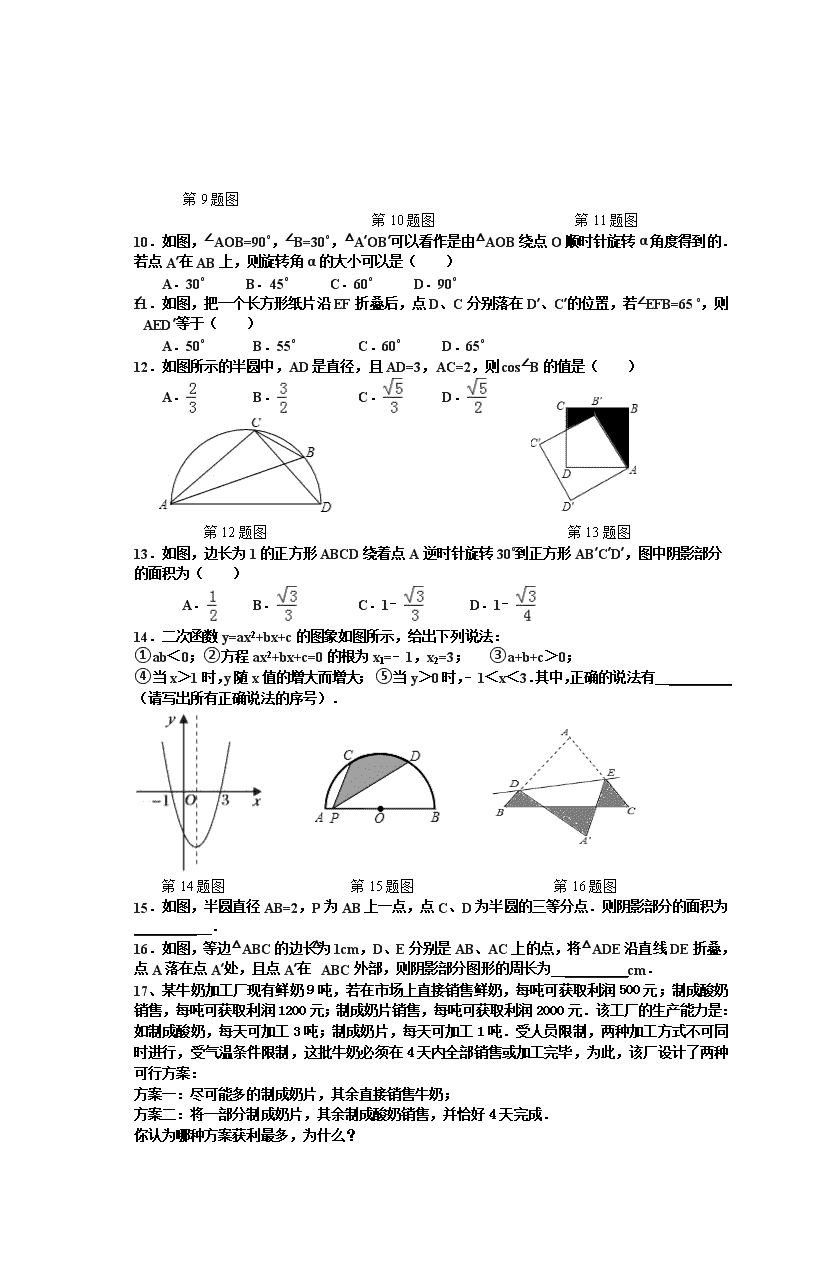若存在，请求出符合条件的点P的坐标；若不存在，请说明理由；‎ ‎（3）在直线AC上方的抛物线上有一点D，使得△DCA的面积最大，求出点D的坐标．‎ 二．选择题 ‎9．如图，菱形ABCD的周长为‎20cm，sin∠BAD=，DE⊥AB于点E，下列结论中：①SABCD=‎15cm2；②BE=‎1cm； ③AC=3BD．正确的个数为（　　）‎ ‎ A．0个 B．1个 C．2个 D．3个 ‎ 第9题图 ‎ 第10题图 第11题图 ‎10．如图，∠AOB=90°，∠B=30°，△A′OB′可以看作是由△AOB绕点O顺时针旋转α角度得到的．若点A′在AB上，则旋转角α的大小可以是（　　）‎ ‎ A．30° B．45° C．60° D．90°‎ ‎11．如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，若∠EFB=65°，则∠AED′等于（　　）‎ A．50° B．55° C．60° D．65°‎ ‎12．如图所示的半圆中，AD是直径，且AD=3，AC=2，则cos∠B的值是（　　）‎ A． B． C． D．‎ ‎ 第12题图 第13题图 ‎13．如图，边长为1的正方形ABCD绕着点A逆时针旋转30°到正方形AB′C′D′，图中阴影部分的面积为（　　）‎ A． B． C．1﹣ D．1﹣‎ ‎14．二次函数y=ax2+bx+c的图象如图所示，给出下列说法：‎ ‎①ab＜0；②方程ax2+bx+c=0的根为x1=﹣1，x2=3； ③a+b+c＞0；‎ ‎④当x＞1时，y随x值的增大而增大； ⑤当y＞0时，﹣1＜x＜3．其中，正确的说法有　_________　（请写出所有正确说法的序号）．‎ ‎ 第14题图 第15题图 第16题图 ‎15．如图，半圆直径AB=2，P为AB上一点，点C、D为半圆的三等分点．则阴影部分的面积为　_________　．‎ ‎16．如图，等边△ABC的边长为‎1cm，D、E分别是AB、AC上的点，将△ADE沿直线DE折叠，点A落在点A′处，且点A′在△ABC外部，则阴影部分图形的周长为　_________cm．‎ ‎17、某牛奶加工厂现有鲜奶9吨，若在市场上直接销售鲜奶，每吨可获取利润500元；制成酸奶销售，每吨可获取利润1200元；制成奶片销售，每吨可获取利润2000元．该工厂的生产能力是：如制成酸奶，每天可加工3吨；制成奶片，每天可加工1吨．受人员限制，两种加工方式不可同时进行，受气温条件限制，这批牛奶必须在4天内全部销售或加工完毕，为此，该厂设计了两种可行方案：‎ 方案一：尽可能多的制成奶片，其余直接销售牛奶；‎ 方案二：将一部分制成奶片，其余制成酸奶销售，并恰好4天完成．‎ 你认为哪种方案获利最多，为什么？‎ ‎18、某化妆品店老板到厂家选购A、B两种品牌的化妆品，若购进A品牌的化妆品5套，B品牌的化妆品6套，需要950元；若购进A品牌的化妆品3套，B品牌的化妆品2套，需要450元．‎ ‎（1）求A、B两种品牌的化妆品每套进价分别为多少元？‎ ‎（2）若销售1套A品牌的化妆品可获利30元，销售1套B品牌的化妆品可获利20元，根据市场需求，化妆品店老板决定，购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套，且B品牌化妆品最多可购进40套，这样化妆品全部售出后，可使总的获利不少于1200元，问有几种进货方案？如何进货？‎ ‎19、某乒乓球训练馆准备购买n副某种品牌的乒乓球拍，每副球拍配k(k≥3)个乒乓球. 已知A、B两家超市都有这个品牌的乒乓球拍和乒乓球出售，且每副球拍的标价都为20元，每个乒乓球的标价都为1元 . 现两家超市正在促销，A超市所有商品均打九折(按原价的90%付费)销售，而B超市买1副乒乓球拍送3个乒乓球 . 若仅考虑购买球拍和乒乓球的费用，请解答下列问题：‎ ‎（1） 如果只在某一家超市购买所需球拍和乒乓球，那么去A超市还是B超市买更合算？‎ ‎（2） 当k＝12时，请设计最省钱的购买方案．‎ ‎20、元旦联欢会前某班布置教室，同学们利用彩纸条粘成一环套一环的彩纸链，小颖测量了部分彩纸链的长度，她得到的数据如下表：‎ 纸环数x（个）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎……‎ 彩纸链长度y（cm）‎ ‎19‎ ‎36‎ ‎53‎ ‎70‎ ‎……‎ ‎（1）把上表中x、y的各组对应值作为点的坐标，在平面直角坐标系中描出相应的点，猜想y与x 的函数关系，并求出函数关系式。‎ ‎（2）教室天花板对角线长‎10m，现需沿天花板对角线各拉一根彩纸链，则每根彩纸链至少要用多少个纸环？‎ ‎21、某养鸡场分3次用鸡蛋孵化出小鸡，每次孵化所用的鸡蛋数、每次的孵化率（孵化率）分别如图1，图2所示：‎ ‎（1）求该养鸡场这3次孵化出的小鸡总数和平均孵化率；‎ ‎（2）如果要孵化出2000只小鸡，根据上面的计算结果，估计该养鸡场要用多少个鸡蛋？‎ ‎22、某学校七年级数学兴趣小组组织一次数学活动．在一座有三道环形路的数字迷宫的每个进口处都标记着一个数，要求进入者把自己当做数“‎1”‎，进入时必须乘进口处的数，并将结果带到下一个进口，依次累乘下去，在通过最后一个进口时，只有乘积是5的倍数，才可以进入迷宫中心，现让一名5岁小朋友小军从最外环任一个进口进入．‎ ‎（1）小军能进入迷宫中心的概率是多少？请画出树状图进行说明 ‎（2）小组两位组员小张和小李商量做一个小游戏，以猜测小军进迷宫的结果比胜负．游戏规则规完：小军如果能进入迷宫中心，小张和小李各得1分；小军如果不能进入迷宫中心，则他在最后一个进口处所得乘积是奇数时，小张得3分，所得乘积是偶数时，小李得3分，你认为这个游戏公平吗？如果公平，请说明理由；如果不公平，请在第二道环进口处的两个数中改变其中一个数使游戏公平．‎ ‎（3）在（2）的游戏规则下，让小军从最外环进口任意进入10次，最终小张和小李的总得分之和不超过28分，请问小军至少几次进入迷宫中心？‎ ‎23、如图，菱形ABCD中，E、F分别为BC、CD上的点，且CE=CF．‎ 求证：AE=AF．‎ ‎24、如图，矩形ABCD中，点E是BC上一点，连接DE、AE， AF⊥DE，垂足为F ，AE平分∠BED．求证：DE＝BC．‎ ‎25、在矩形纸片ABCD中，将矩形纸片沿BD折叠，使点A落在点E处，设DE与BC相交于点F．‎ ‎（1）求证：△BEF≌△DCF；‎ ‎（2）若AB＝6，BC＝8，求BF的长；‎ ‎26、如图，菱形ABCD的边长为2，BD=2，E、F分别是边AD，CD上的两个动点，且满足AE+CF=2.‎ ‎（1）求证：△BDE≌△BCF； ‎ ‎（2）判断△BEF的形状，并说明理由；‎ ‎27、一座建于若干年前的水库大坝的横断面如图所示，其中背水面的整个坡面是长为‎90米、宽为‎5米的矩形. 现需将其整修并进行美化，方案如下：① 将背水坡AB的坡度由1∶0.75改为1∶ ；② 用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域，依次相间地种草与栽花 ．‎ ‎（1） 求整修后背水坡面的面积；‎ ‎（2） 如果栽花的成本是每平方米25元，种草的成本是每平方米20元，那么种植花草至少需要多少元？‎ ‎28、如图，为平行四边形，，，交的延长线于点，交于点．‎ A D F E B C ‎（1）求证：；‎ ‎（2）若AC=2CF，∠ADC=60°，AC⊥DC，求的长；‎ ‎29、如图，在△ABC中，∠A、∠B的平分线交于点D，DE∥AC交BC于点E，DF∥BC交AC于点F．‎ ‎（1）点D是△ABC的________心；‎ ‎（2）求证：四边形DECF为菱形．‎ ‎ ‎ ‎30、已知：如图△ABC是等边三角形，过AB边上的点D作DG∥BC，交AC于点G，‎ 在GD的延长线上取点E，使DE=DB，连结AE、CD。‎ ‎（1）求证：△AGE≌DAC；‎ ‎（2）过点E作EF∥DC，交BC于点F，请你连结AF，并判断△AEF是怎样的三角形，‎ 并说明理由。‎ ‎31、如图，在△ABE中，BA＝BE，C在BE上，D在AB上，且AD＝AC＝BC.‎ F ‎（1）若∠B＝40°，求∠BCD的大小;‎ ‎（2）过C作CF∥AB交AE于F, 求证：CF=BD.‎ A B C D O E F M N ‎32、如图，O为平行四边形ABCD的对角线AC的中点，过点O作一条直线分别与AB、CD交于点M、N，点E、F在直线MN上，且OE=OF。‎ ‎ （1）图中共有几对全等三角形，请把它们都写出；‎ ‎ （2）求证：∠MAE=∠NCF。‎ ‎33、如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．‎ B C CC C A G D F E ‎ ‎⑴求证：CE＝CF；‎ ‎⑵在图中，若G在AD上，且∠GCE＝45°，‎ 则GE＝BE＋GD成立吗？为什么？‎ ‎34、如图，在正方形ABCD中，E是AB边上任一点，BG⊥CE，垂足为点O，交AC于点F，交AD于点G。‎ ‎（1）证明：BE＝AG ‎（2）点E位于什么位置时，∠AEF＝∠CEB？说明理由。‎ ‎35、如图，在中，，，点，分别在，‎ C D B F E A AC上，把沿着对折，使点落在上点处，且使.‎ ‎(1)猜测与的数量关系，并说明理由；‎ ‎(2)求证：四边形是菱形.‎ ‎36、已知一次函数y=kx+b(k、b为常数，且k≠0)，x与y的部分对应值如下表所示，那么不等式kx+b<0的解集是（ ）‎ x ‎-2‎ ‎-1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ y ‎3‎ ‎2‎ ‎2‎ ‎0‎ ‎-1‎ ‎-2‎ A.x<0 B.x>‎0 C.x<1 D.x>1‎ ‎37、地面的瓷砖如图，一把钥匙被藏在某种颜色的一块瓷砖下面，下列判断正确的是（　　）‎ A．被藏在白色瓷砖下的概率大 B．被藏在黑色瓷砖下的概率大 C．被藏在两种瓷砖下的概率一样大 D．无法确定 ‎38、若是方程组的解,则m,n的值分别为（ ）‎ A.m=2,n=1 B.m=2,n=‎3 C.m=1,n=8 D.m=－2,n=3‎ ‎39、将一副三角板按如图所示的位置叠放，则△AOB与△DOC的面积之比等于（ ）A. B. C. D. ‎ ‎ 第39题图 ‎40、一个圆锥形的圣诞帽高为10cm，母线长为‎15cm，则圣诞帽的表面积为____cm2(结果保留π)．‎ ‎41、如果代数式的值为－4，那么代数式的值为 ．‎ A B C P E F M ‎42、已知二次函数的图像向左平移2个单位，向下平移1个单位后得到二次函数的图像，则二次函数的解析式为_________．‎ ‎43、观察下列等式：‎ 第一个等式是1+2=3， 第二个等式是2+3=5，‎ 第三个等式是4+5=9， 第四个等式是8＋9=17，‎ ‎……猜想：第n个等式是 ．‎ ‎44、Rt△ABC中，∠BAC=90°，AB=3，AC=4，P为边BC 上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，‎ 则AM的最小值为 ．‎ ‎45、如图某幢大楼顶部有广告牌CD．张老师目高MA为‎1.60米，他站立在离大楼‎45米的A处测得大楼顶端点D的仰角为；接着他向大楼前进‎14米站在点B处，测得广告牌顶端点C的仰角为．(计算结果保留一位小数)‎ ‎(1)求这幢大楼的高DH；‎ ‎(2)求这块广告牌CD的高度．‎ ‎46、已知： A是⊙O上一点，半径OC的延长线与过点A的直线交于B点，OC＝BC，AC＝OB．‎ ‎(1)试判断直线AB与⊙O的位置关系，并说明理由；‎ ‎(2)若D为⊙O上一点，∠ACD＝45°，AD＝，求扇形OAC的面积．‎ A D B O C 第46题图 ‎13.由于受到“三鹿奶粉事件”影响，惠客超市销售的蒙牛纯牛奶销量呈下降趋势，为了扩大销量，减少库存，商场决定降价销售. 已知每箱以60元销售，平均每天可销售40箱，进价为每箱45元.价格每降低1元，平均每天多销售20箱，设每箱降价x元（x为正整数），‎ ‎（1）写出平均每天销售y（箱）与x（元）之间的函数关系式及自变量x的取值范围；‎ ‎（2）如何定价才能能使超市平均每天销售这种牛奶的利润最大？最大利润为多少？‎ ‎47、为了解某校学生早餐就餐情况，四位同学做了不同的调查：小华调查初一年级三个班的全体同学；小明调查初二年级三个班的全体同学；小芳调查初三年级全体同学；小兰从初一、初二、初三三个年级中分别抽取了一个班同学做了调查，你认为抽样调查较科学的是( ) A．小兰 B．小明 C．小芳   D．小华 ‎ ‎48、某公司把500万元资金投入新产品的生产，第一年获得一定的利润，在不抽掉资金和利润的前提下，继续生产，第二年的利润率提高8%，若第二年的利润达到112万元，设第一年的利润率为x，则方程可以列为 A．500(1+x)(1+x+8%)=112 B．500(1+x)(1+x+8%)=112 +500‎ C．500(1+x)·8%=112 D．500(1+x)(x+8%)=112‎ ‎49、二次函数的图象的顶点坐标是( )‎ B A O A.（－2，3） B.（2，3） C.（－2，－3） D.（2，－3） ‎ ‎50、如图，扇形OAB是一个圆锥的侧面展开图，若小正方形方格 的边长为1,则这个圆锥的底面半径为( )‎ A. B. C. D. ‎ ‎51、横坐标、纵坐标都是整数的点叫做整点，函数y＝的图象上整点的个数是( )‎ ‎　A．3个　　　B．4个　　　C．6个　　　D．8个 第54题图 第52题图 第53题图 ‎52、如图，在边长为1的等边三角形ABC中，点D是AC的中点，点P是BC边的中垂线MN上任一点，则PC＋PD的最小值为 ．‎ ‎53、某校九年级学生准备毕业庆典，打算用橄榄枝花圈来装饰大厅圆柱．已知大厅圆柱高‎4米，底面周长‎1米．由于在中学同学三年，他们打算精确地用花圈从上往下均匀缠绕圆柱3圈（如图53），那么螺旋形花圈的长至少 米．‎ 第55题图 ‎54、将正整数按如图所示的规律排列下去．若用有序实数对（，）表示第排，从左到右第个数，如（4，3）表示实数9，则（7，2）表示的实数是 ．‎ ‎55、早晨小欣与妈妈同时从家里出发，步行与自行车向相反 方向的两地上学与上班，如图是他们离家的路程（米）与时 间（分钟）之间的函数图象，妈妈骑车走了10分钟时接到小 欣的电话，立即以原速度返回并前往学校，若已知小欣步行的 速度为50米/分钟，并且妈妈与小欣同时到达学校．完成下 列问题：‎ ‎（1）在坐标轴两处的括号内填入适当的数据；‎ ‎（2）求小欣早晨上学需要的时间．‎ ‎56、对于点O、M，点M沿MO的方向运动到O左转弯继续运动到N，使OM＝ON，且OM⊥ON，这一过程称为M点关于O点完成一次“左转弯运动”．正方形ABCD和点P，P点关于A左转弯运动到P1，P1关于B左转弯运动到P2，P2关于C左转弯运动到P3，P3关于D左转弯运动到P4，P4关于A左转弯运动到P5，……．‎ ‎（1）请你在图中用直尺和圆规在图中确定点P1的位置；‎ ‎（2）以D为原点、直线AD为轴建立直角坐标系，并且已知点B在第二象限，A、P两点的坐标为（0，4）、（1，1），请你推断：P2008、P2009、P2010三点的坐标．‎ 第56题图 图1‎ 图2‎ ‎ ‎ ‎57、已知如图1，点P是正方形ABCD的BC边上一动点，AP交对角线BD于点E，过点B作BQ⊥AP于G点，交对角线AC于F，交边CD于Q点．‎ ‎（1）小聪在研究图形时发现图中除等腰直角三角形外，还有几对三角形全等．请你写出其中三对全等三角形，并选择其中一对全等三角形证明．‎ 第57题图 图1‎ 图2‎ ‎（2）小明在研究过程中连结PE，提出猜想：在点P运动过程中，是否存在∠APB＝∠CPF？若存在，点P应满足何条件？并说明理由；若不存在，为什么？‎