中考复习之—三角形与四边形练习题含答案 9页

中考复习之——三角形与四边形 ‎1、三角形与平行四边形联手 例1、如图1，在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.试判断AF与CE是否相等，并说明理由.‎ 解：∵四边形ABCD为平行四边形 ∴AB=CD，∠A=∠C，∠ADC=∠CBA ∵DF平分∠ADC，BE平分∠CBA ∴∠ADF=1/2∠ADC=1/2∠CBA=∠CBE 在△ADF和△CBE中 ∠A=∠C AD=BC ∠ADF=∠CBE ∴△ADF≌△CBE（ASA） ∴AF=CE ‎2、三角形与矩形联手 例2、如图5， 矩形ABCD中，点E是BC上一点，AE＝AD，DF⊥AE于F，连结DE，求证：DF＝DC．‎ 证明：∵AE=AD ∴∠AED=∠ADE ∵AD‖BC ∴∠CED=∠ADE ∴∠CED=∠AED ∵∠DFE=∠C=90 ∠CED=∠AED（已证） DE=DE（公共边） ∴△DFE≌△DCE（AAS） ∴DF=DC 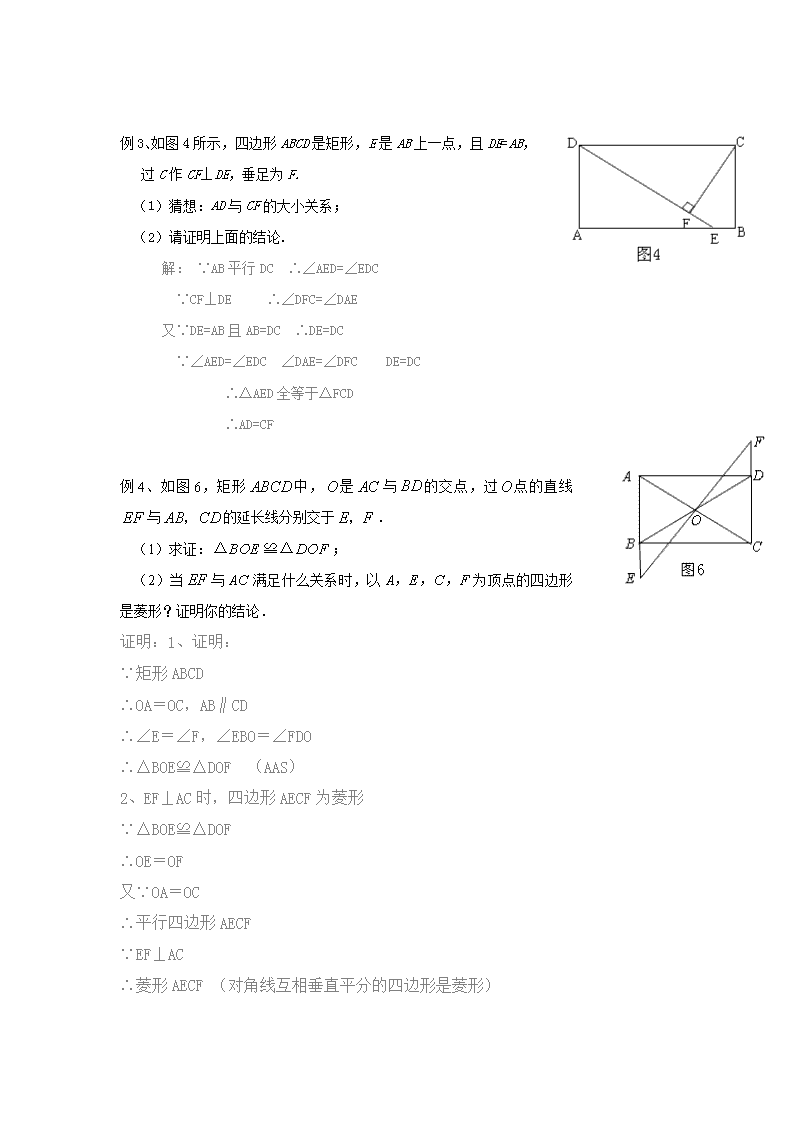例3、如图4所示，四边形ABCD是矩形，E是AB上一点，且DE=AB，‎ 过C作CF⊥DE，垂足为F. ‎ ‎（1）猜想：AD与CF的大小关系；‎ ‎（2）请证明上面的结论. ‎ ‎ 解： ∵AB平行DC ∴∠AED=∠EDC ∵CF⊥DE ∴∠DFC=∠DAE 又∵DE=AB且AB=DC ∴DE=DC ∵∠AED=∠EDC ∠DAE=∠DFC DE=DC ∴△AED全等于△FCD ∴AD=CF 例4、如图6，矩形中，是与的交点，过点的直线与的延长线分别交于．‎ ‎ （1）求证：；‎ ‎ （2）当与满足什么关系时，以为顶点的四边形是菱形？证明你的结论．‎ 证明：1、证明： ∵矩形ABCD ∴OA＝OC，AB∥CD ∴∠E＝∠F，∠EBO＝∠FDO ∴△BOE≌△DOF （AAS） 2、EF⊥AC时，四边形AECF为菱形 ∵△BOE≌△DOF ∴OE＝OF 又∵OA＝OC ∴平行四边形AECF ∵EF⊥AC ∴菱形AECF （对角线互相垂直平分的四边形是菱形）‎ 例5、在矩形ABCD中，AB=2，AD=．‎ ‎（1）在边CD上找一点E，使EB平分∠AEC，并加以说明；‎ ‎（2）若P为BC边上一点，且BP=2CP，连接EP并延长交AB的延长线于F．‎ ‎ ①求证：点B平分线段AF；‎ ‎ ②△PAE能否由△PFB绕P点按顺时针方向旋转而得到，若能，加以证明，并求出旋转度数；若不能，请说明理由．‎ 解：（1）∵∠AEB=∠BEC=∠ABE ‎∴∠AEB=∠ABE AB=AE=2‎ DE=1(勾股定理计算)‎ ‎∴DE=EC=1‎ E 是DC 的中点 ‎（2）∵⊿ECP∽⊿FBP ‎∴EC/BF=PC/PB=1/2‎ ‎∴BF=2‎ 点B平分线段AF ‎②由（1）知⊿AED≌⊿BEC ⊿ABE 是等边三角形 在⊿PEC 中 tan∠PEC=√3/3 ∴∠PEC=30º=∠F ∴⊿AEF 是直角三角形 ∴AF=2AE=2AB ‎3、三角形与正方形联手 例6、如图8所示，四边形ABCD是正方形，G是CD边上的一个动点(点G与C、D不重合)，以CG为一边在正方形ABCD外作正方形CEFG，连结BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系： ‎ ‎（1）①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系；‎ ‎②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度 ‎，得到如图2、如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断． ‎ ‎（2）将原题中正方形改为矩形（如图4—6），且AB=a，BC=b，CE=ka， CG=kb (ab，k0)，第(1)题①中得到的结论哪些成立，哪些不成立？若成立，以图5为例简要说明理由．（08年义乌市）‎ ‎（3）在第(2)题图5中，连结、，且a=3，b=2，k=，求的值．‎ 解：（1）①BG⊥DE，BG=DE； ②∵四边形ABCD和四边形CEFG是正方形， ∴BC=DC，CG=CE，∠BCD=∠ECG=90°， ∴∠BCG=∠DCE， ∴△BCG≌△DCE， ∴BG=DE，∠CBG=∠CDE， 又∵∠CBG+∠BHC=90°， ∴∠CDE+∠DHG=90°， ∴BG⊥DE．‎ ‎（2）∵AB=a，BC=b，CE=ka，CG=kb，‎ ‎∴BC/DC ＝CG/CE =b/a ，‎ 又∵∠BCG=∠DCE，‎ ‎∴△BCG∽△DCE，‎ ‎∴∠CBG=∠CDE，‎ 又∵∠CBG+∠BHC=90°，‎ ‎∴∠CDE+∠DHG=90°，‎ ‎∴BG⊥DE．‎ ‎（3）连接BE、DG．‎ 根据题意，得AB=3，BC=2，CE=1.5，CG=1，‎ ‎∵BG⊥DE，∠BCD=∠ECG=90°‎ ‎∴BE2+DG2=BO2+OE2+DO2+OG2=BC2+CD2+CE2+CG2=9+4+2.25+1=16.25‎ 例7、如图9-甲，在△ABC中，∠ACB为锐角．点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．‎ 解答下列问题：‎ ‎（1）如果AB=AC，∠BAC=90º．‎ ①当点D在线段BC上时（与点B不重合），如图9-乙，线段CF、BD之间的位置关系为 ▲ ，数量关系为 ▲ ．‎ ②当点D在线段BC的延长线上时，如图9-丙，①中的结论是否仍然成立，为什么？‎ ‎ ‎ ‎ （2）如果AB≠AC，∠BAC≠90º，点D在线段BC上运动．试探究：当△ABC满足一个什么条件时，CF⊥BC（点C、F重合除外）？画出相应图形，并说明理由．（画图不写作法）‎ ‎（3）若AC＝，BC=3，在（2）的条件下，设正方形ADEF的边DE与线段CF相交于点P，求线段CP长的最大值．‎ 解：（1）①CF与BD位置关系是 垂直、数量关系是相等；‎ ‎②当点D在BC的延长线上时①的结论仍成立．‎ 由正方形ADEF得 AD=AF ，∠DAF=90º．‎ ‎∵∠BAC=90º，∴∠DAF=∠BAC ， ∴∠DAB=∠FAC，‎ 又AB=AC ，∴△DAB≌△FAC ， ∴CF=BD 　　‎ ‎ ∠ACF=∠ABD．‎ ‎∵∠BAC=90º， AB=AC ，∴∠ABC=45º，∴∠ACF=45º，‎ ‎∴∠BCF=∠ACB+∠ACF= 90º．即 CF⊥BD ‎（2）画图正确　‎ 当∠BCA=45º时，CF⊥BD（如图丁）．‎ ‎ 理由是：过点A作AG⊥AC交BC于点G，∴AC=AG 可证：△GAD≌△CAF ∴∠ACF=∠AGD=45º ‎ ‎∠BCF=∠ACB+∠ACF= 90º． 即CF⊥BD ‎（3）当具备∠BCA=45º时，‎ 过点A作AQ⊥BC交BC的延长线于点Q，（如图戊）‎ ‎∵DE与CF交于点P时， ∴此时点D位于线段CQ上，‎ ‎∵∠BCA=45º，可求出AQ= CQ=4．设CD=x ，∴ DQ=4―x，‎ 容易说明△AQD∽△DCP，∴ ， ∴，‎ ‎． ‎ ‎∵0＜x≤3 ∴当x=2时，CP有最大值1． ‎ ‎4三角形与梯形联手 例8、已知：如图11，梯形中，，点是的中点，的延长线与的延长线相交于点．‎ ‎（1）求证： 和全等 ‎（2）连结，判断四边形的形状，并证明你的结论．‎ ‎1、证明： ∵AD∥BC ∴∠CFE＝∠BAE，∠FCE＝∠ABE ∵E是BC的中点 ∴BE＝CE ∴△ABE≌△FCE （AAS） ∴‎ AB＝CF 2、菱形ABFC 证明： ∵AD∥BC，AB＝CF ∴平行四边形ABFC ∵△ADC沿AE折叠至△AEC，∠D＝90 ∴∠AEC＝∠D＝90 ∴AF⊥BC ∴菱形ABFC 例9、如图12，在等腰梯形中，，是的中点，求证：．‎ ‎（1）证明：∵四边形ABCD是等腰梯形，‎ ‎∴AB=DC，∠A=∠D．‎ ‎∵M是AD的中点，‎ ‎∴AM=DM．‎ 在△ABM和△DCM中，‎ ‎ AB＝DC ∠A＝∠D AM＝DM ∴△ABM≌△DCM（SAS）．‎ ‎∴MB=MC．‎ 例10、 如图13所示，已知等腰梯形ABCD中，AD∥BC，AB=DC，AC与BD相交于点O．请在图中找出一对全等的三角形，并加以证明．‎ 解：∵ ABCD是等腰梯形 ∴AB=DC ∠ABC=∠DCB ‎ BC是公共边 ∴△ABC≌△DCB(SAS)‎ 还有△ABD≌△DCA(SAS)‎ ‎ ∵AD‖BC ∠ABC=∠DCB ‎ ∴∠BAD=∠CDA ‎ AD是公共边 ‎ ‎ 且AB=DC ‎ ∴△ABD≌△DCA(SAS)‎ 例11、已知：如图14，在梯形ABCD中，AD∥BC，BC=DC，CF平分∠BCD，DF∥AB，BF的延长线交DC于点E。‎ 求证：（1）△BFC≌△DFC；（2）AD=DE ‎（1）△BFC≌△DFC　　因为CF平分∠BCD， 所以：∠DCF＝∠BCF又：BC＝DC，　公共边CF＝CF　　所以△BFC≌△DFC（两边夹一角，边角边定理）‎ （2） 延长DF交BC于H;因AD‖BC，DF‖AB，所以四边形ABHD是平行四边形 AD＝BH 因△BFC≌△DFC 所以DF＝BF　∠FDE＝∠FBH 又∠DFE＝∠BFH所以：△DFE≌△BFH 所以DE＝BH（全等三角行的对应边和角相等）又AD＝BH;所以：AD＝DE