新修订版全国各地中考数学试题分类汇编考点26直角三角形与勾股定理含答案 22页

‎ 直角三角形与勾股定理A 一、选择题 ‎1. （2011山东滨州，9，3分）在△ABC中,∠C=90°, ∠C=72°,AB=10,则边AC的长约为(精确到0.1)（ ）‎ A.9.1‎‎ B.‎9.5 C.3.1 D.3.5‎ ‎【答案】C ‎2. （2011山东烟台，7,4分）如图是油路管道的一部分，延伸外围的支路恰好构成一个直角三角形，两直角边分别为‎6m和‎8m.按照输油中心O到三条支路的距离相等来连接管道，则O到三条支路的管道总长（计算时视管道为线，中心O为点）是（ ）‎ A‎2m B‎.3m C‎.6m D‎.9m O ‎（第7题图）‎ ‎【答案】C ‎3. （2011台湾全区，29）已知小龙、阿虎两人均在同一地点，若小龙向北直走160公尺，再向东直走80公尺后，可到神仙百货，则阿虎向西直走多少公尺后，他与神仙百货的距离为340公尺？‎ A． 100 B． ‎180 C． 220 D． 260‎ ‎【答案】Ｃ ‎4. （2011湖北黄石，7，3分）将一个有45度角的三角板的直角顶点放在一张宽为‎3cm的纸带边沿上，另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30度角，如图(3)，则三角板的最大边的长为 A. ‎3cm B. ‎6cm C. ‎3‎cm D. 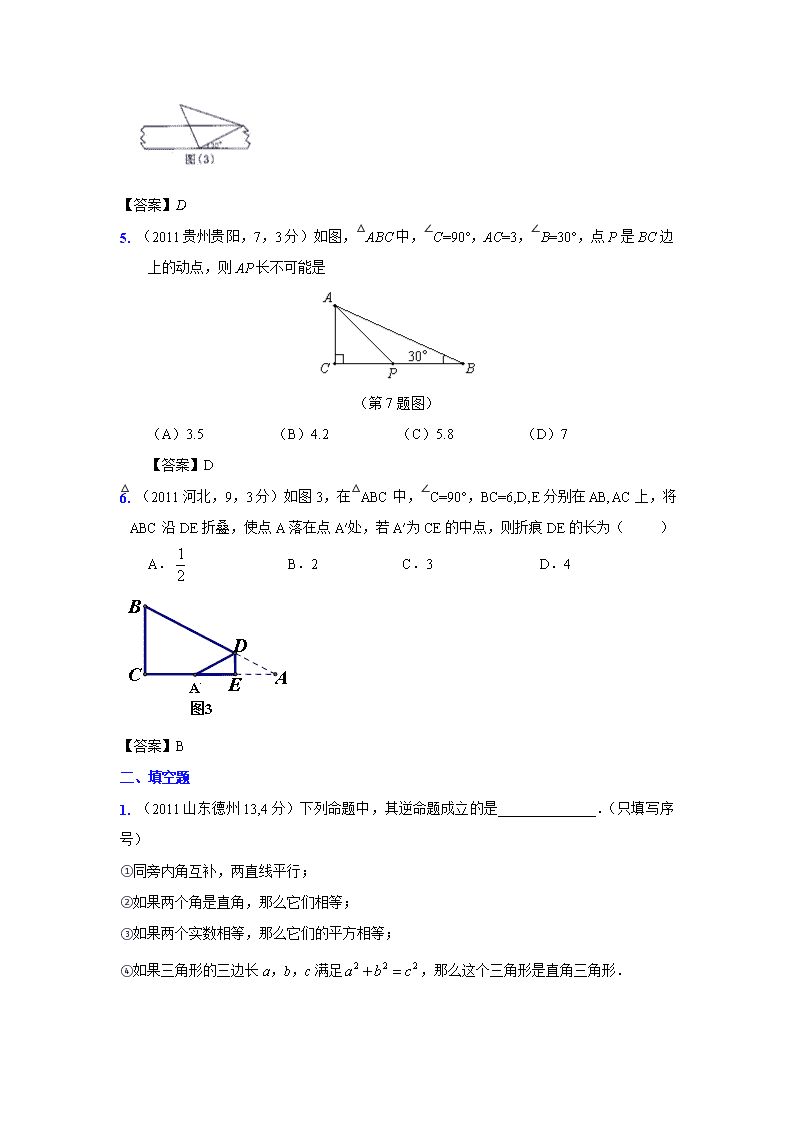‎6‎cm ‎【答案】D ‎5. （2011贵州贵阳，7，3分）如图，△ABC中，∠C=90°，AC=3，∠B=30°，点P是BC边上的动点，则AP长不可能是 ‎（第7题图）‎ ‎ （A）3.5 （B）4.2 （C）5.8 （D）7‎ ‎ 【答案】D ‎6. （2011河北，9，3分）如图3，在△ABC中，∠C=90°，BC=6,D,E分别在AB,AC上，将△ABC沿DE折叠，使点A落在点A′处，若A′为CE的中点，则折痕DE的长为（ ）‎ A． B．‎2 C．3 D．4 ‎ ‎【答案】B 二、填空题 ‎1. （2011山东德州13,4分）下列命题中，其逆命题成立的是______________．（只填写序号）‎ ‎①同旁内角互补，两直线平行；‎ ‎②如果两个角是直角，那么它们相等；‎ ‎③如果两个实数相等，那么它们的平方相等；‎ ‎④如果三角形的三边长a，b，c满足，那么这个三角形是直角三角形．‎ ‎【答案】① ④‎ ‎2. （2011浙江温州，16，5分）我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”（如图1）．图2由弦图变化得到，它是用八个全等的直角三角形拼接而成，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1,S2，S3．‎ ‎ 若S1，S2，S3＝10，则S2的值是 ．‎ ‎【答案】‎ ‎3. (2011重庆綦江，16，4分) 一个正方体物体沿斜坡向下滑动，其截面如图所示.正方形DEFH的边长为‎2米，坡角∠A＝30°,∠B＝90°,BC＝‎6米. 当正方形DEFH运动到什么位置,即当AE＝ 米时,有DC＝AE＋BC. ‎ ‎ ‎ ‎【答案】：‎ ‎4. （2011四川凉山州，15，4分）把命题“如果直角三角形的两直角边长分别为a、b，斜边长为c，那么”的逆命题改写成“如果……，那么……”的形式： ‎ ‎ 。‎ ‎【答案】如果三角形三边长a，b，c，满足，那么这个三角形是直角三角形 ‎【答案】5‎ ‎6. （2011广东肇庆，13，3分）在直角三角形ABC中，∠C ＝ 90°，BC ＝ 12，AC ＝ 9，则AB＝ ▲ ．‎ ‎【答案】15‎ ‎7. （2011贵州安顺，16，4分）如图，在Rt△ABC中，∠C=90°，BC=‎6cm，AC=‎8cm，按图中所示方法将△BCD沿BD折叠，使点C落在AB边的C′点，那么△ADC′的面积是 ．‎ 第16题图 ‎【答案】‎6cm2‎ ‎8. （2011山东枣庄，15，4分）将一副三角尺如图所示叠放在一起，若=‎14cm，则阴影部分的面积是________cm2. ‎ A C E D B F ‎30°‎ ‎45°‎ ‎【答案】‎ 三、解答题 ‎1. （2011四川广安，28，10分）某园艺公司对一块直角三角形的花圃进行改造．测得两直角边长为‎6m、‎8m.现要将其扩建成等腰三角形，且扩充部分是以‎8m为直角边的直角三角形．求扩建后的等腰三角形花圃的周长．‎ ‎【答案】由题意可得，花圃的周长=8+8+=16+‎ ‎2. （2011四川绵阳23，12）‎ 王伟准备用一段长‎30米的篱笆围成一个三角形形状的小圈，用于饲养家兔.已知第一条边长为a米，由于受地势限制，第二条边长只能是第一条边长的2倍多‎2米.‎ ‎(1)请用a表示第三条边长；‎ ‎(2)问第一条边长可以为‎7米吗？为什么?请说明理由，并求出a的取值范围；‎ ‎(3)能否使得围成的小圈是直角三角形形状，且各边长均为整数？若能，说明你的围法;若不能，请说明理由.‎ ‎【答案】(1)第一条边为a,第二条边为‎2a+2,第三条边为30-a-（‎2a+2）=28‎‎-3a ‎(2)不可以是7，∵第一条边为7，第二条边为16，第三条边为7，不满足三边之间的关系，不可以构成三角形。＞a＞5‎ ‎(3)5,12,13,可以围成一个满足条件的直角三角形 ‎3. （2011江西南昌，25，10分）某数学兴趣小组开展了一次活动，过程如下：‎ 设∠BAC=（0°＜＜90°）.现把小棒依次摆放在两射线AB，AC之间，并使小棒两端分别落在两射线上.‎ 活动一：‎ 如图甲所示，从点A1开始，依次向右摆放小棒，使小棒与小棒在两端点处互相垂直，A‎1A2为第1根小棒.‎ 数学思考：‎ ‎（1）小棒能无限摆下去吗？答： .（填“能”或“不能”）‎ ‎（2）设AA1=A‎1A2=A‎2A3=1.‎ ‎①= 度；‎ ‎②若记小棒A2n‎-1A2n的长度为an（n为正整数，如A‎1A2=a1,A‎3A4=a2,）,求此时a2，a3的值，并直接写出an（用含n的式子表示）.‎ 图甲 活动二：‎ 如图乙所示，从点A1开始，用等长的小棒依次向右摆放，其中A‎1A2为第1根小棒，且A‎1A2= AA1.‎ 数学思考：‎ ‎（3）若已经向右摆放了3根小棒，则= ，= ，= ；（用含的式子表示）‎ ‎（4）若只能摆放4根小棒，求的范围.‎ 图乙 ‎【答案】解：（1）能 ‎（2）①22.5°‎ ‎②方法一：‎ ‎∵AA1=A‎1A2=A‎2A3=1， A‎1A2⊥A‎2A3，∴A‎1A3=，AA3=1+.‎ 又∵A‎2A3⊥A‎3A4，∴A‎1A2∥A‎3A4.同理：A‎3A4∥A‎5A6，∴∠A=∠AA‎2A1=∠AA‎4A3=∠AA‎6A5，‎ ‎∴AA3=A‎3A4，AA5=A‎5A6，∴a2= A‎3A4=AA3=1+,a3=AA3+A‎3A5=a2+A‎3A5.∵A‎3A5=a2,‎ ‎∴a3=A‎5A6=AA5=a2+a2=(+1)2.‎ 方法二：‎ ‎∵AA1=A‎1A2=A‎2A3=1， A‎1A2⊥A‎2A3，∴A‎1A3=，AA3=1+.‎ 又∵A‎2A3⊥A‎3A4，∴A‎1A2∥A‎3A4.同理：A‎3A4∥A‎5A6，∴∠A=∠AA‎2A1=∠AA‎4A3=∠AA‎6A5，‎ ‎∴a2=A‎3A4=AA3=1+,又∵∠A‎2A3A4=∠A‎4A5A6=90°，∠A‎2A4A3=∠A‎4A6A5，∴△A‎2A3A4∽△A‎4A5A6，‎ ‎∴，∴a3==(+1)2.‎ an=(+1)n-1.‎ ‎(3)‎ ‎(4)由题意得，∴15°＜≤18°.‎ ‎4. （2011四川乐山25，12分）如图,在直角△ABC中, ∠ACB=90,CD⊥AB,垂足为D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F,若AC=mBC,CE=nEA(m,n为实数).试探究线段EF与EG的数量关系.‎ ‎ ‎ (1) 如图(14.2),当m=1,n=1时,EF与EG的数量关系是 ‎ 证明:‎ (2) ‎ 如图(14.3),当m=1,n为任意实数时,EF与EG的数量关系是 ‎ 证明 (3) 如图(14.1),当m,n均为任意实数时,EF与EG的数量关系是 ‎ ‎(写出关系式,不必证明)‎ ‎5. （2011四川乐山18，3分）如图，在直角△ABC中，∠C=90，∠CAB的平分线AD交BC于D，若DE垂直平分AB，求∠B的度数。‎ ‎【答案】‎ ‎ 解：∵AD平分∠CAD ‎ ∴∠CAD=∠BAD ‎∵DE垂直平分AB ‎∴AD=BD,∠B=∠BAD ‎∴∠CAD=∠BAD=∠B ‎∵在RtΔABC中，∠C=90º ‎∴∠CAD+∠DAE+∠B=90º ‎∴∠B=30º ‎6. （2011山东枣庄，21，8分）如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题：‎ ‎（1）画线段AD∥BC且使AD =BC，连接CD；‎ ‎（2）线段AC的长为 ，CD的长为 ，AD的长为 ；‎ ‎（3）△ACD为 三角形，四边形ABCD的面积为 ；‎ ‎（4）若E为BC中点，则tan∠CAE的值是 ．‎ A B C E 解：（1）如图； ……………………………1分 A B C E 第21题图 D ‎（2），，5； ………………4分 ‎（3）直角，10； ……………………6分 ‎（4）． ……………………………8分 ‎ 直角三角形与勾股定理B 一、选择题 ‎1. （2011湖北十堰，5，3分）如图，Rt△ABC中，∠ACB=900，DE过点C，且DE//AB，若∠ACD=500，则∠B的度数是（ ）‎ 第5题图 A．500 B．‎400 C．300 D．250‎ ‎【答案】B ‎2. （2011湖北随州，11，3分）下列说法中 ‎①一个角的两边分别垂直于另一个角的两边，则这两个角相等 ‎②数据5，2，7，1，2，4的中位数是3，众数是2‎ ‎③等腰梯形既是中心对称图形，又是轴对称图形 ‎④Rt△ABC中，∠C=90°，两直角边a，b分别是方程x2－7x＋7=0的两个根，则AB边上的中线长为 正确命题有（ ）‎ A．0个 B．1个 C．2个 D．3个 ‎【答案】C ‎3. （2011内蒙古呼和浩特市，9,3分）如图所示，四边形ABCD中，DC∥AB，BC=1，AB=AC=AD=2.则BD的长为 （ ）‎ A. B. C. D. ‎ ‎【答案】B 二、填空题 ‎1. （2011广东河源，9,4分）如图1,在 Rt△ABC中,∠B=90°.ED是AC的垂直平分线,交AC于点D,交BC于点E,已知∠BAE=30°,则∠C的度数为°　　　　　　　　　　‎ ‎【答案】300‎ ‎2. （2011黑龙江省哈尔滨市，20，3分）如图，在Rt△ABC中，∠ACB=90°，点D是斜边AB的中点，DE⊥AC,垂足为E，若DE=2，CD=,则BE的长为 _。‎ ‎【答案】‎ ‎3. (湖南湘西,5,3分)如图，在Rt△ABC中，∠C=90°，若BC=3,AC=4,则AB的长是______.‎ ‎【答案】5‎ ‎4. （2011山西，18，3分）如图，已知AB=12，AB⊥BC于B，AB⊥AD于A，AD=5，BC=10，点E是CD的中点，则AE的长是_______.‎ ‎（第18题）‎ ‎【答案】；‎ ‎5. 如（2011贵州遵义，15，4分）图，由四个边长为1的小正方形构成一个大正方形，连接小正方形的三个顶点，可得到△ABC，则△ABC中BC边上的高是 ▲ 。‎ ‎【答案】‎ ‎6. （2011广东肇庆，13，3分）在直角三角形ABC中，∠C＝90°，BC＝12，AC＝9，则AB＝ ▲ ．‎ ‎【答案】15‎ ‎7. （2011黑龙江绥化，10，3分）已知三角形相邻两边长分别为20和30，第三边上的高为10，则此三角形的面积为 .‎ ‎【答案】或（答案不全或含错解，本题不得分）‎ ‎8. （2011江西b卷，15,3分）一块直角三角板放在两平行直线上，如图所示,∠1+∠2=___________度.‎ ‎11111‎ ‎1‎ ‎2‎ 第15题 ‎【答案】90°‎ ‎9. （2011江苏徐州，13,3分）若直角三角形的一个锐角为20°，则另一个锐角等于 ▲ °‎ ‎【答案】70°‎ ‎10．（2011山东枣庄，15，4分）将一副三角尺如图所示叠放在一起，若=‎14cm，则阴影部分的面积是________cm2. ‎ A C E D B F ‎30°‎ ‎45°‎ ‎【答案】‎ 三、解答题 ‎2. （2011湖北潜江天门仙桃江汉油田，23，10分）两个大小相同且含角的三角板ABC和DEC如图①摆放，使直角顶点重合. 将图①中△DEC绕点C逆时针旋转得到图②，点F、G分别是CD、DE与AB的交点，点H是DE与AC的交点. ‎ ‎（1）不添加辅助线，写出图②中所有与△BCF全等的三角形；‎ ‎（2）将图②中的△DEC绕点C逆时针旋转得△D1E‎1C，点F、G、H的对应点分别为F1、G1、H1 ，如图③.探究线段D‎1F1与AH1之间的数量关系，并写出推理过程； ‎ ‎ （3）在（2）的条件下，若D1E1与CE交于点I，求证：G1I =CI.‎ ‎【答案】解：（1）图②中与△BCF全等的有△GDF、 △GAH 、△ECH．‎ ‎（2）= ‎ 证明：∵∴△AF‎1C ≌△D1H‎1C. ‎ ‎∴ F‎1C= H‎1C， 又CD1=CA，‎ ‎∴CD1- F‎1C =CA- H‎1C.即 ‎（3）连结CG1.‎ 在△D‎1G1F1和△AG1H1中，‎ ‎∵，∴△D‎1G1F1 ≌△AG1H1.‎ ‎∴G‎1F1=G1H1‎ 又∵H‎1C=F‎1C，G‎1C=G‎1C，∴△CG‎1F1 ≌△CG1H1.‎ ‎∴∠1=∠2. ‎ ‎∵∠B=60°，∠BCF=30° ，∴∠BFC=90°. ‎ 又∵∠DCE=90°，∴∠BFC=∠DCE， ‎ ‎∴BA∥CE， ∴∠1=∠3， ∴∠2=∠3，‎ ‎∴G1I=CI.‎ ‎ 直角三角形与勾股定理C 一、选择题 ‎1. （2011湖北十堰，5，3分）如图，Rt△ABC中，∠ACB=900，DE过点C，且DE//AB，若∠ACD=500，则∠B的度数是（ ）‎ 第5题图 A．500 B．‎400 C．300 D．250‎ ‎【答案】B ‎2. （2011湖北随州，11，3分）下列说法中 ‎①一个角的两边分别垂直于另一个角的两边，则这两个角相等 ‎②数据5，2，7，1，2，4的中位数是3，众数是2‎ ‎③等腰梯形既是中心对称图形，又是轴对称图形 ‎④Rt△ABC中，∠C=90°，两直角边a，b分别是方程x2－7x＋7=0的两个根，则AB边上的中线长为 正确命题有（ ）‎ A．0个 B．1个 C．2个 D．3个 ‎【答案】C ‎3. （2011内蒙古呼和浩特市，9,3分）如图所示，四边形ABCD中，DC∥AB，BC=1，AB=AC=AD=2.则BD的长为 （ ）‎ A. B. C. D. ‎ ‎【答案】B ‎4. （2011昭通，6，3）将一副直角三角板如图2所示放置，使含300‎ 角的三角板的一条直角边和含450角的三角板的一条直角边重合，则∠1的度数为（ ）‎ ‎ A．450 B．‎600 C．750 D．850‎ ‎1‎ ‎ 图2‎ ‎【答案】C ‎5. （2011•泸州，11，2分）如图，在Rt△ABC中，∠ABC=90°，∠C=60°，AC=10，将BC向BA方向翻折过去，使点C落在BA上的点C′，折痕为BE，则EC的长度是（　　）‎ ‎ A、 B、 ‎ C、 D、 ‎【答案】B．‎ ‎6. （2011贵州黔南，5,4分）如图，△ABC中,AB=AC=6,BC=8，AE平分∠BAC交BC于点E,点D为AB的中点，连接DE,则△BDE的周长是（ ）‎ A.7+ B‎.10 C.4+2 D.12‎ A D B E C 第5题图 ‎【答案】B 二、填空题 ‎1. （2011广东河源，9,4分）如图1,在 Rt△ABC中,∠B=90°.ED是AC的垂直平分线,交AC于点D,交BC于点E,已知∠BAE=30°,则∠C的度数为°　　　　　　　　　　‎ ‎【答案】300‎ ‎3. (湖南湘西,5,3分)如图，在Rt△ABC中，∠C=90°，若BC=3,AC=4,则AB的长是______.‎ ‎【答案】5‎ ‎4. （2011山西，18，3分）如图，已知AB=12，AB⊥BC于B，AB⊥AD于A，AD=5，BC=10，点E是CD的中点，则AE的长是_______.‎ ‎（第18题）‎ ‎【答案】；‎ ‎5. 如（2011贵州遵义，15，4分）图，由四个边长为1的小正方形构成一个大正方形，连接小正方形的三个顶点，可得到△ABC，则△ABC中BC边上的高是 ▲ 。‎ ‎【答案】‎ ‎6. （2011广东肇庆，13，3分）在直角三角形ABC中，∠C＝90°，BC＝12，AC＝9，则AB＝ ▲ ．‎ ‎【答案】15‎ ‎7. （2011黑龙江绥化，10，3分）已知三角形相邻两边长分别为20和30，第三边上的高为10，则此三角形的面积为 .‎ ‎【答案】或（答案不全或含错解，本题不得分）‎ ‎8. （2011江西b卷，15,3分）一块直角三角板放在两平行直线上，如图所示,∠1+∠2=___________度.‎ ‎11111‎ ‎1‎ ‎2‎ 第15题 ‎【答案】90°‎ ‎9. （2011江苏徐州，13,3分）若直角三角形的一个锐角为20°，则另一个锐角等于 ▲ °‎ ‎【答案】70°‎ ‎10．（2011山东枣庄，15，4分）将一副三角尺如图所示叠放在一起，若=‎14cm，则阴影部分的面积是________cm2. ‎ A C E D B F ‎30°‎ ‎45°‎ ‎【答案】‎ ‎11. （2011云南玉溪，14，3分）如图，在△ABC中，∠ABC=90°，分别以BC、AB、AC为边向外作正方形，面积分别记为S1、S2、S3，若S2=4，S3=6，则S1=________.‎ ‎【答案】2.‎ ‎12. （2011新疆维吾尔自治区，新疆生产建设兵团，11，5分）如图，△ABC是等边三角形，AB=‎4cm，则BC边上的高AD等于_____________cm； ‎ 第11题图 ‎【答案】‎ 三、解答题 ‎1. (湖南湘西,20,6分)如图，在△ABC中，AD⊥BC,垂足为D，∠B=60°,∠C=45°.‎ ‎(1)求∠BAC的度数。‎ ‎（2）若AC=2,求AD的长。‎ 解: (1)∠BAC=180°-60°-45°=75°‎ ‎(2) ∵AD⊥BC,∴△ADC是直角三角形,‎ ‎∵∠C=45°, ∴∠DAC=45°,根据勾股定理,得AD=.‎ ‎2. （2011湖北潜江天门仙桃江汉油田，23，10分）两个大小相同且含角的三角板ABC和DEC如图①摆放，使直角顶点重合. 将图①中△DEC绕点C逆时针旋转得到图②，点F、G分别是CD、DE与AB的交点，点H是DE与AC的交点. ‎ ‎（1）不添加辅助线，写出图②中所有与△BCF全等的三角形；‎ ‎（2）将图②中的△DEC绕点C逆时针旋转得△D1E‎1C，点F、G、H的对应点分别为F1、G1、H1 ，如图③.探究线段D‎1F1与AH1之间的数量关系，并写出推理过程； ‎ ‎ （3）在（2）的条件下，若D1E1与CE交于点I，求证：G1I =CI.‎ ‎【答案】解：（1）图②中与△BCF全等的有△GDF、 △GAH 、△ECH．‎ ‎（2）= ‎ 证明：∵∴△AF‎1C ≌△D1H‎1C. ‎ ‎∴ F‎1C= H‎1C， 又CD1=CA，‎ ‎∴CD1- F‎1C =CA- H‎1C.即 ‎（3）连结CG1.‎ 在△D‎1G1F1和△AG1H1中，‎ ‎∵，∴△D‎1G1F1 ≌△AG1H1.‎ ‎∴G‎1F1=G1H1‎ 又∵H‎1C=F‎1C，G‎1C=G‎1C，∴△CG‎1F1 ≌△CG1H1.‎ ‎∴∠1=∠2. ‎ ‎∵∠B=60°，∠BCF=30° ，∴∠BFC=90°. ‎ 又∵∠DCE=90°，∴∠BFC=∠DCE， ‎ ‎∴BA∥CE， ∴∠1=∠3， ∴∠2=∠3，‎ ‎∴G1I=CI.‎