2010中考数学试题分类二次函数的图象和性质1 57页

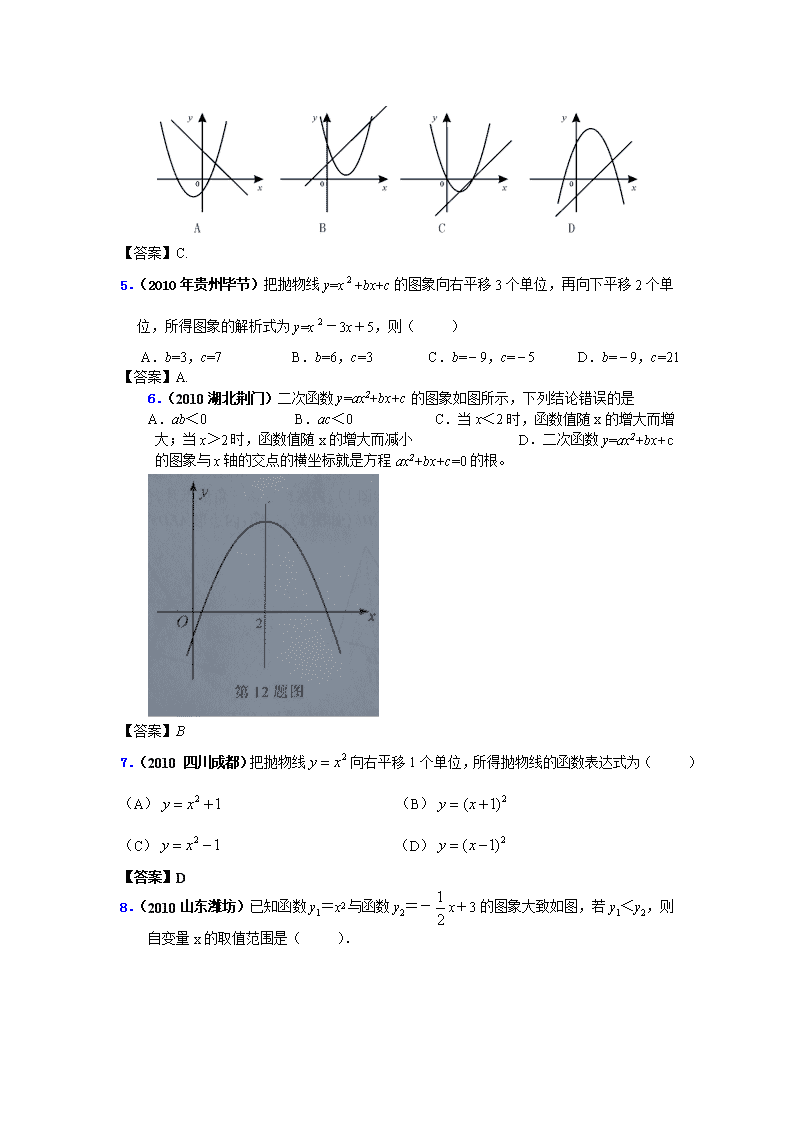
一、选择题 ‎1．（2010福建福州）已知二次函数y＝Ax2＋Bx＋C的图象如图所示，则下列结论正确的是( )‎ ‎ A．a＞0 B．c＜0 C．b2－4ac＜0 D．a＋b＋c＞0‎ ‎(第10题)‎ ‎【答案】D ‎ ‎2．（2010 河北）如图5，已知抛物线的对称轴为，点A，‎ B均在抛物线上，且AB与x轴平行，其中点A的坐标为 ‎（0，3），则点B的坐标为 O x y A 图5‎ x = 2‎ B A．（2，3） B．（3，2） ‎ C．（3，3） D．（4，3）‎ ‎【答案】D ‎ ‎3．（2010 山东莱芜）二次函数的图象如图所示，则一次函数的 图象不经过 x ‎（第9题图）‎ y O A．第一象限 B．第二象限 ‎ C．第三象限 D．第四象限 ‎【答案】D ‎ ‎4．（2010年贵州毕节）函数在同一直角坐标系内的图象大致是( ) ‎ ‎【答案】C.‎ ‎5．（2010年贵州毕节）把抛物线y=x+bx+c的图象向右平移3个单位，再向下平移2个单位，所得图象的解析式为y=x－3x＋5，则（ 　　）‎ A．b=3，c=7　　　　　B．b=6，c=3 C．b=9，c=5　　　D．b=9，c=21‎ ‎【答案】A.‎ ‎6．（2010湖北荆门）二次函数y=ax2+bx+c的图象如图所示，下列结论错误的是 A．ab＜0 B．ac＜0 C．当x＜2时，函数值随x的增大而增大；当x＞2时，函数值随x的增大而减小 D．二次函数y=ax2+bx+c的图象与x轴的交点的横坐标就是方程ax2+bx+c=0的根。‎ ‎【答案】B ‎ ‎7．（2010 四川成都）把抛物线向右平移1个单位，所得抛物线的函数表达式为（ ）‎ ‎（A） （B）‎ ‎（C） （D）‎ ‎【答案】D ‎ ‎8．（2010山东潍坊）已知函数y1＝x2与函数y2＝－x＋3的图象大致如图，若y1＜y2，则自变量x的取值范围是（ ）．‎ A．－＜x＜2 B．x＞2或x＜－ ‎ C．－2＜x＜ D． x＜－2或x＞‎ ‎【答案】C ‎ ‎9．（2010湖北荆州）若把函数y=x的图象用E（x，x）记，函数y=2x+1的图象用E（x，2x+1）记，……则E（x，）可以由E（x，）怎样平移得到？‎ ‎ A．向上平移１个单位 　B．向下平移１个单位 C．向左平移１个单位 D．向右平移１个单位 ‎【答案】D ‎10．（2010湖北鄂州）二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论①a、b异号；②当x=1和x=3时，函数值相等；③4a+b=0，④当y=4时，x的取值只能为0．结论正确的个数有（ ） 个 A．1　　　Ｂ．2　　　Ｃ．3　　　Ｄ．4‎ ‎【答案】C ‎ ‎11．（2010湖北省咸宁）已知抛物线（＜0）过A（，0）、O（0，0）、‎ B（，）、C（3，）四点，则与的大小关系是 A．＞ B． C．＜ D．不能确定 ‎【答案】A ‎ ‎12．（2010北京） 将二次函数y＝x2－2x＋3，化为y＝(x－h)2＋k的形式，结果为（ ）‎ A．y＝(x＋1)2＋4 B．y＝(x－1)2＋4‎ C．y＝(x＋1)2＋2 D． y＝(x－1)2＋2‎ ‎【答案】D ‎ ‎13．（2010山东泰安）下列函数：①；②；③；④，其中的值随值增大而增大的函数有（ ）‎ A、4个 B、3个 C、2个 D、1个 ‎【答案】B ‎ ‎14．（2010四川乐山）.设a、b是常数，且b＞0，抛物线y=ax2+bx+a2-5a-6为下图中四个图象之一，则a的值为（ ）‎ y x O y x O y x O ‎1‎ ‎－1‎ y x O ‎1‎ ‎－1‎ A. 6或－1 B. －6或1 C. 6 D. －1‎ ‎【答案】D ‎ ‎15．（2010黑龙江哈尔滨）在抛物线上的一个点是（ ）‎ ‎ （A）（4，4） （B）（1，－4） （C）（2，0） （D）．（0，4）‎ ‎【答案】C ‎ ‎16．（2010江苏徐州）平面直角坐标系中，若平移二次函数y=(x-2009)(x-2010)+4的图象，使其与x轴交于两点，且此两点的距离为1个单位，则平移方式为 ‎ A．向上平移4个单位 B．向下平移4个单位 ‎ C．向左平移4个单位 D．向右平移4个单位 ‎【答案】B ‎ ‎17．（2010陕西西安）已知抛物线，将抛物线C平移得到抛物线若两条抛物线C、 关于直线对称，则下列平移方法中，正确的是 ‎ A．将抛物线C向右平移个单位 B．将抛物线C向右平移3个单位 ‎ C．将抛物线C向右平移5个单位 D．将抛物线C向右平移6个单位 ‎【答案】C ‎ ‎18．（2010 福建三明）抛物线的图象和x轴有交点，则k的取值范围是 （ ）‎ ‎ A． B．且C． D．且 ‎【答案】B ‎ ‎19．（2010 山东东营） 二次函数的图象如图所示，则一次函数与反比例函数在同一坐标系内的图象大致为（ ）‎ ‎1‎ O x y ‎（第12题图）‎ y x O ‎(B)‎ y x O ‎(A)‎ y x O ‎(C)‎ y x O ‎(D)‎ ‎【答案】B ‎20．（2010安徽蚌埠）已知函数，并且是方程的两个根，则 实数的大小关系可能是 ‎ A． 　 B．　 C． 　D．‎ ‎【答案】D ‎21．（2010安徽省中中考） 若二次函数配方后为则、的值分别为 ‎………………（ ）‎ A）0.5 B）0.1 C）—4.5 D）—4.1‎ ‎【答案】C ‎22．（2010甘肃兰州） 二次函数的图像的顶点坐标是 ‎ A．（-1，8） B．（1，8） C．（-1，2） D．（1，-4）‎ ‎【答案】A ‎23．（2010甘肃兰州） 抛物线图像向右平移2个单位再向下平移3个单位，所得图像的解析式为，则b、c的值为 ‎ A . b=2， c=2 B. b=2，c=0 ‎ ‎ C . b= -2，c=-1 D. b= -3， c=2‎ ‎【答案】B ‎24．（2010甘肃兰州） 抛物线图像如图所示，则一次函数与反比例函数 在同一坐标系内的图像大致为 x x x x x 第15题图 ‎【答案】D ‎25．（2010江苏盐城）给出下列四个函数：①；②；③；④．时，y随x的增大而减小的函数有 A．1个 B．2个 C．3个 D．4个 ‎【答案】C ‎26．（2010山东烟台）如图，AB为半圆的直径，点P为AB上一动点，动点P从点A出发，沿AB匀速运动到点B，运动时间为t，分别以AP于PB为直径做半圆，则图中阴影部分的面积S与时间t之间的函数图像大致为 ‎【答案】D ‎ ‎27．（2010台湾）坐标平面上有一函数y=24x2-48的图形，其顶点坐标为何？ (A) (0，-2) (B) (1，-24) (C) (0，-48) (D) (2，48) 。 【答案】C ‎ ‎28．（2010台湾） 坐标平面上，若移动二次函数y=2(x-175)(x-176)+6的图形，使其与x轴交于两点，且此两点的距离为1单位，则移动方式可为下列哪一种？ (A) 向上移动3单位 (B) 向下移动3单位 (C) 向上移勤6单位 (D) 向下移动6单位 。‎ ‎【答案】D ‎ ‎29．（2010浙江杭州）定义[]为函数的特征数, 下面给出特征数为 [2m，1 – m , –1– m] ‎ 的函数的一些结论： ‎ ‎ ① 当m = – 3时，函数图象的顶点坐标是(，)； ‎ ‎ ② 当m > 0时，函数图象截x轴所得的线段长度大于； ‎ ‎ ③ 当m < 0时，函数在x >时，y随x的增大而减小；‎ ‎ ④ 当m ¹ 0时，函数图象经过同一个点.‎ ‎ 其中正确的结论有 ‎ A. ①②③④ B. ①②④ C. ①③④ D. ②④‎ ‎【答案】B ‎30．（2010 嵊州市）已知二次函数的图象如图所示,记,则与的大小关系为 ( )‎ A. B. C. D.、大小关系不能确定 ‎【答案】C ‎ ‎31．（2010 浙江台州市）如图，点A，B的坐标分别为（1, 4）和（4, 4）,抛物线的顶点在线段AB上运动，与x轴交于C、D两点（C在D的左侧），点C的横坐标最小值为，则点D的横坐标最大值为(▲)‎ ‎ ‎ y x O ‎（第10题）‎ ‎ A．－3 　 B．1 C．5 D．8 ‎ ‎【答案】D ‎32．（2010浙江金华） 已知抛物线的开口向下,顶点坐标为（2，－3） ,‎ 那么该抛物线有（ ▲ ）‎ ‎ A. 最小值 －3 B. 最大值－3 C. 最小值2 D. 最大值2‎ ‎【答案】B ‎ ‎33．（2010 山东济南）在平面直角坐标系中，抛物线与轴的交点的个数是（ ）‎ A．3 B．2 C．1 D．0‎ ‎【答案】B ‎ ‎34．（2010 浙江衢州）下列四个函数图象中，当x＞0时，y随x的增大而增大的是（　　）‎ O y x ‎1‎ ‎1‎ A．‎ O y x ‎1‎ ‎1‎ C．‎ O y x ‎1‎ ‎1‎ D．‎ O y x ‎1‎ ‎1‎ B．‎ ‎【答案】C ‎ ‎35.（2010 浙江衢州） 如图，四边形ABCD中，∠BAD=∠ACB=90°，AB=AD，AC=4BC，‎ 设CD的长为x，四边形ABCD的面积为y，则y与x之间的 函数关系式是（　　）‎ ‎(第10题)‎ A B C D A． B． ‎ C． D．‎ ‎36．（2010 天津）已知二次函数()的图象如图所示，有下列结论：‎ ‎①；‎ ‎②；‎ ‎③；‎ ‎④．‎ ‎ 其中，正确结论的个数是 ‎（A）1‎ ‎（B）2‎ ‎（C）3‎ ‎（D）4‎ 第（10）题 y x O ‎【答案】D ‎ ‎37．（2010 内蒙古包头）已知二次函数的图象与轴交于点、，且，与轴的正半轴的交点在的下方．下列结论：①；②；③；④．其中正确结论的个数是 个．‎ ‎【答案】4‎ ‎38．（2010广西桂林）将抛物线绕它的顶点旋转180°，所得抛物线的解析式是（ ）．‎ ‎ A． B． EMBED Equation.DSMT4 ‎ C． D．‎ ‎【答案】D ‎ ‎39．（2010 四川自贡）y=x2＋（1－a）x＋1是关于x的二次函数，当x的取值范围是1≤x≤3时，y在x＝1时取得最大值，则实数a的取值范围是（ ）。‎ A．a=5 B．a≥5 C．a＝3 D．a≥3 ‎ ‎【答案】B ‎ ‎40．（2010宁夏回族自治区）把抛物线向左平移1个单位，然后向上平移3个单位，则平移后抛物线的表达式 （ ）‎ A． B． C． EMBED Equation.DSMT4 D．．‎ ‎【答案】B ‎ ‎41．（2010 湖北咸宁）已知抛物线（＜0）过A（，0）、O（0，0）、‎ B（， EMBED Equation.3 ）、C（3，）四点，则与的大小关系是 A．＞ B． C．＜ D．不能确定 ‎【答案】A ‎ ‎42．（2010 广西钦州市）已知二次函数（a≠0）的图象如图所示，则下列结论：‎ ‎① ac >0； ② a–b +c <0； ③当x <0时，y <0；‎ ‎④方程（a≠0）有两个大于－1的实数根．‎ ‎•‎ ‎•‎ 其中错误的结论有 ‎ ‎（A）② ③ （B）② ④ （C）① ③ （D）① ④‎ 第18题 x =1‎ ‎【答案】C ‎ ‎43．（2010青海西宁）下列哪一个函数，其图象与轴有两个交点 A. B. ‎ C. D. ‎ ‎【答案】D ‎ ‎44．（2010鄂尔多斯）已知二次函数中函数y与自变量x之间的部分对应值如下表所示，点A(x1，y1) ，B(x2，y2)在函数的图象上，当00 ‎ C．b= -4a D．关于x的方程ax2+bx+c=0的根是x1=－1,x2=5‎ 图7‎ ‎-1‎ y x ‎5‎ x=2‎ ‎2‎ O ‎【答案】B ‎ ‎46．（2010云南昭通）二次函数y=ax2+bx+c的图象如图3所示，则下列结论正确的是（ ）‎ A．a<0，b<0，c>0，b2－4ac>0; B．a>0，b<0，c>0，b2－4ac<0; ‎ C．a<0，b>0，c<0，b2－4ac>0; D．a<0，b>0，c>0，b2－4ac>0;‎ 图3‎ y x O ‎【答案】D ‎ ‎47．（2010贵州遵义）如图，两条抛物线y1=-χ2+1、y2=χ2-1 与分别经过点（-2，0），（2，0）且平行于y轴的两条平行线围成的阴影部分的面积为 A．8 B．6 C．10 D．4‎ ‎【答案】A ‎48．（2010广西柳州）抛物线y=-x2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：‎ x ‎…‎ ‎-2‎ ‎-1‎ ‎0‎ ‎1‎ ‎2‎ ‎…‎ y ‎…‎ ‎0‎ ‎4‎ ‎6‎ ‎6‎ ‎4‎ ‎…‎ ‎ ‎ 从上表可知，下列说法正确的个数是 ‎①抛物线与x轴的一个交点为（-2，0） ②抛物线与y轴的交点为（0，6）‎ ‎③抛物线的对称轴是：x=1 ④在对称轴左侧y随x的增大而增大 A．1 B．2 C．3 D．4‎ ‎【答案】C ‎ ‎49．（2010湖北宜昌）抛物线的顶点坐标是（ ）。‎ A. (0,-1) B. (-1,1) C. (-1,0) D.(1,0)‎ ‎【答案】C ‎50．（2010广西百色）二次函数的图象如图所示，下列几个结论：‎ ‎①对称轴为; ②当≤0时,＜0或＞4；③函数解析式为；‎ ‎④当≤0时，随的增大而增大. 其中正确的结论有（ ）‎ A. ①②③④ B. ①②③ C. ①③④ D. ①③‎ 第13题 ‎【答案】C ‎ ‎51．（2010四川攀枝花）如图３，二次函数ｙ＝ａx－ｂｘ＋２的大致图像如图所示，‎ 则函数ｙ＝－ａx＋ｂ的图像不经过（ ）‎ A．第一象限 B．第二象限 ‎ C．第三象限 D．第四象限 ‎ ‎ ‎‎2‎ O 图3‎ X Y 图13(备用图)‎ C O X Y ‎【答案】A ‎ ‎52．（2010 福建莆田）某同学利用描点法画二次函数（的图象时，列出的部分数据如下表：‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎3‎ ‎0‎ ‎-2‎ ‎0‎ ‎3‎ 经检查，发现表格中恰好有一组数据计算错误，请你根据上述信息写出该二次函数的解 析式： ‎ ‎【答案】‎ ‎【答案】C ‎ ‎53．（2010江苏泰州）下列函数中，y随x增大而增大的是（ ）‎ A. B. C. D. ‎ ‎【答案】A 二、填空题 ‎1．（2010 湖南株洲）已知二次函数（为常数），当取不同的值时，其图象构成一个“抛物线系”．下图分别是当，，，时二次函数的图象.它们的顶点在一条直线上，这条直线的解析式是 .‎ ‎【答案】‎ ‎2．（2010湖南郴州）将抛物线y=x2 +1向下平移2个单位，则此时抛物线的解析式是_____________．‎ ‎【答案】 y=x2 －1‎ ‎3．（2010江苏扬州）y＝2x2－bx＋3的对称轴是直线x＝1，则b的值为__________．‎ ‎【答案】4‎ ‎4．（2010山东泰安）将y=2x2-12x-12变为y=a（x-m）2+n的形式，则m·n= .‎ ‎【答案】-90‎ ‎5．（2010湖北襄樊）将抛物线向上平移2个单位，再向右平移1个单位后，得到的抛物线的解析式为____________．‎ ‎ ．【答案】或 ‎6．（2010江苏 镇江）已知实数的最大值为 .‎ ‎【答案】4‎ ‎7．（2010 湖南株洲）二次函数的图象与轴的交点如图所示，根据图中信息可得到的值是 ．‎ ‎·‎ ‎【答案】4‎ ‎8．（2010安徽蚌埠）已知抛物线经过点A(4,0)。设点C（1，-3），请在抛物线的对称轴上确定一点D,使得的值最大，则D点的坐标为＿＿＿＿＿＿＿。 ‎ ‎【答案】﹝2,-6﹞‎ ‎9．（2010江苏盐城）写出图象经过点(1，－1)的一个函数关系式 ▲ ．‎ ‎【答案】y=-x或y=-或y=x2-2x，答案不唯一 ‎10．（2010山东日照）如图，是二次函数y=ax2+bx+c图象的一部分，其对称轴为直线x=1，若其与x轴一交点为A（3，0），则由图象可知，不等式ax2+bx+c＜0的解集是 .‎ ‎【答案】－1＜x＜3‎ ‎11．（2010浙江宁波） 如图，已知⊙P的半径为2，圆心P在抛物线上运动，当⊙P与轴相切时，圆心P的坐标为 ▲ .‎ ‎12．（2010 四川泸州）在平面直角坐标系中，将二次函数y=（x-2）2+2的图像向左平移2个单位，所得图像对应的解析式为 ．‎ ‎【答案】y=x2+2‎ ‎13．（2010 云南玉溪）如图7是二次函数在平面直 角坐标系中的图象，根据图形判断 ① ＞0；‎ ② ++＜0； ③ 2-＜0；‎ ④ 2+8＞4中正确的是（填写序号） ．‎ 图7‎ ‎【答案】② 、④‎ ‎14．（2010 天津）已知二次函数()中自变量和函数值的部分对应值如下表：‎ ‎…‎ ‎0‎ ‎1‎ ‎…‎ ‎…‎ ‎0‎ ‎…‎ 则该二次函数的解析式为 ．‎ ‎【答案】‎ ‎15．（2010青海西宁）将抛物线先向左平移1个单位后所得到的新抛物线的表达式为 .‎ ‎【答案】‎ ‎16．（2010吉林长春）如图，抛物线交x轴于点G、F，交y轴于点D，在x轴上方的抛物线上有两点B、E，它们关于y轴对称，点G、B在y轴左侧。BA⊥OG于点A，BC⊥OD于点C。四边形OABC与四边形ODEF的面积分别为6和10，则△ABG与△BCD的面积之和为 。‎ ‎【答案】4‎ ‎17．（2010新疆维吾尔自治区新疆建设兵团）抛物线y=-x2+bx+c的部分图象如图所示，若y＞0，则x的取值范围是_______。‎ ‎【答案】.-3＜x＜1‎ ‎18．（2010辽宁本溪）如图所示，已知抛物线y=ax2+bx+c(a≠0)经过原点和点（-2，0），则2a-3b 0.(＞、＜或＝)‎ O x y ‎-2‎ ‎【答案】＞‎ ‎19．（2010黑龙江绥化）抛物线与x轴的一个交点的坐标为（l,0), 则此抛物线与x轴的另一个交点的坐标是 .‎ ‎【答案】（3，0）‎ ‎20．（2010湖南娄底）二次函数y=(x－1)2－2的图像的对称轴是直线_____________. ‎ ‎【答案】x=1 ‎ ‎【答案】或(对一个得2分)‎ ‎21．（2010 浙江义乌）（1）将抛物线y1＝2x2向右平移2个单位，得到抛物线y2的图象，则y2= ▲ ；‎ ‎ （2）如图，P是抛物线y2对称轴上的一个动点，直线x＝t平行于y轴，分别与直线y＝x、抛物线y2交于点A、B．若△ABP是以点A或点B为直角顶点的等腰直角三角形，求满足条件的t的值，则t＝ ▲ ．‎ P y x ‎·‎ ‎【答案】（1）2(x－2)2 或 （2）3、1、、‎ ‎22．（2010浙江金华）若二次函数的部分图象如图所示，则关于x 的一元二次方程的一个解，另一个解 ▲ ；‎ y ‎(第15题图)‎ O x ‎1‎ ‎3‎ ‎【答案】-1‎ 三、解答题 ‎1．（2010江苏泰州）如图，二次函数的图象经过点D，与x轴交于A、B两点．‎ ‎⑴求的值；‎ ‎⑵如图①，设点C为该二次函数的图象在x轴上方的一点，直线AC将四边形ABCD的面积二等分，试证明线段BD被直线AC平分，并求此时直线AC的函数解析式；‎ ‎⑶设点P、Q为该二次函数的图象在x轴上方的两个动点，试猜想：是否存在这样的点P、Q，使△AQP≌△ABP？如果存在，请举例验证你的猜想；如果不存在，请说明理由．（图②供选用）‎ ‎【答案】⑴ ∵抛物线经过点D()‎ ‎∴‎ ‎∴c=6.‎ ‎⑵过点D、B点分别作AC的垂线，垂足分别为E、F，设AC与BD交点为M，‎ ‎　∵AC 将四边形ABCD的面积二等分，即：S△ABC=S△ADC ∴DE=BF ‎ 又∵∠DME=∠BMF， ∠DEM=∠BFE ‎∴△DEM≌△BFM ‎∴DM=BM 即AC平分BD ‎ ‎∵c=6. ∵抛物线为 ‎∴A（）、B（）‎ ‎∵M是BD的中点 ∴M（）‎ 设AC的解析式为y=kx+b，经过A、M点 解得 直线AC的解析式为.‎ ‎⑶存在．设抛物线顶点为N(0，6)，在Rt△AQN中，易得AN=，于是以A点为圆心，AB=为半径作圆与抛物线在x上方一定有交点Q，连接AQ，再作∠QAB平分线AP交抛物线于P，连接BP、PQ，此时由“边角边”易得△AQP≌△ABP．‎ ‎2．（2010福建福州）如图，在△ABC中，∠C＝45°，BC＝10，高AD＝8，矩形EFPQ的一边QP在BC边上，E、F两点分别在AB、AC上，AD交EF于点H．‎ ‎ （1）求证：＝；‎ ‎ （2）设EF＝x，当x为何值时，矩形EFPQ的面积最大?并求其最大值；‎ ‎（3）当矩形EFPQ的面积最大时，该矩形EFPQ以每秒1个单位的速度沿射线QC匀速运动(当点Q与点C重合时停止运动)，设运动时间为t秒，矩形EFFQ与△ABC重叠部分的面积为S，求S与t的函数关系式．‎ ‎ ‎ ‎(第21题)‎ ‎【答案】解：（1）∵ 四边形EFPQ是矩形，∴ EF∥QP．‎ ‎ ∴ △AEF∽△ABC．‎ ‎ 又∵ AD⊥BC， ∴ AH⊥EF．‎ ‎ ∴ ＝ ‎（2）由（1）得＝． AH＝x．‎ ‎ ∴ EQ＝HD＝AD－AH＝8－x，‎ ‎∴ S矩形EFPQ＝EF·EQ＝x (8－x) ＝－x2＋8 x＝－（x－5）2＋20．‎ ‎∵ －＜0， ∴ 当x＝5时，S矩形EFPQ有最大值，最大值为20．‎ ‎（3）如图1，由（2）得EF＝5，EQ＝4．‎ 第21题图1‎ ‎ ‎ ‎∴ ∠C＝45°， ∴ △FPC是等腰直角三角形．‎ ‎ ∴ PC＝FP＝EQ=4，QC＝QP＋PC＝9．‎ 分三种情况讨论：‎ ‎① 如图2．当0≤t＜4时，‎ ‎ 设EF、PF分别交AC于点M、N，则△MFN是等腰直角三角形．∴ FN＝MF＝t．‎ ‎∴S＝S矩形EFPQ－SRt△MFN=20－t2＝－t2＋20；‎ ‎②如图3，当4≤t<5时，则ME＝5－t，QC＝9－t．‎ ‎∴ S＝S梯形EMCQ＝[（5－t）＋（9－t ）]×4＝－4t＋28；‎ ‎③如图4，当5≤t≤9时，设EQ交AC于点K，则KQ=QC＝9－t．‎ ‎ ∴ S＝S△KQC= (9－t)2＝( t－9)2．‎ ‎ ‎ 第21题图2 第21题图3 第21题图4‎ 综上所述：S与t的函数关系式为：‎ S=‎ ‎3．（2010福建福州）如图1，在平面直角坐标系中，点B在直线y＝2x上，过点B作x轴的垂线，垂足为A，OA＝5．若抛物线y＝x2＋bx＋c过O、A两点．‎ ‎（1）求该抛物线的解析式；‎ ‎（2）若A点关于直线y＝2x的对称点为C，判断点C是否在该抛物线上，并说明理由；‎ ‎(第22题图1) (第22题图2)‎ ‎（3）如图2，在（2）的条件下，⊙O1是以BC为直径的圆．过原点O作⊙O1的切线OP，P为切点(点P与点C不重合)．抛物线上是否存在点Q，使得以PQ为直径的圆与⊙O1相切?若存在，求出点Q的横坐标；若不存在，请说明理由．‎ ‎【答案】解：（1）把O（0，0）、A（5，0)分别代入y＝x2＋bx＋c，‎ 得解得 ‎∴ 该抛物线的解析式为y＝x2－x．‎ ‎（2）点C在该抛物线上．‎ ‎ 理由：过点C作CD⊥x轴于点D，连结OC，设AC交OB于点E．‎ ‎ ∵ 点B在直线y＝2x上， ∴ B(5，10)‎ ‎ ∵ 点A、C关于直线y＝2x对称，‎ ‎ ∴ OB⊥AC，CE＝AE，BC⊥OC，OC＝OA＝5，BC＝BA＝10．‎ ‎ 又∵ AB⊥x轴，由勾股定理得OB＝5．‎ ‎∵ SRt△OAB＝AE·OB＝OA·AB，‎ ‎ ∴ AE＝2， ∴ AC＝4．‎ ‎ ∵ ∠OBA十∠CAB＝90°，∠CAD＋∠CAB＝90°， ∴ ∠CAD＝∠OBA．‎ ‎ 又∵ ∠CDA＝∠OAB＝90°， ∴ △CDA∽△OAB．‎ ‎ ∴ ＝＝ ∴ CD＝4，AD＝8 ∴ C（－3，4）‎ ‎ 当x＝－3时，y＝×9－×(－3)＝4．‎ ‎∴ 点C在抛物线y＝x2－x上．‎ ‎（3）抛物线上存在点Q，使得以PQ为直径的圆与⊙O1相切．‎ ‎ 过点P作PF⊥x轴于点F，连结O1P，过点O1作O1H⊥x轴于点H．‎ ‎ ∴ CD∥O1H∥BA． ∵ C(－3，4)，B(5，10)，‎ ‎ ∴ O1是BC的中点． ∴ 由平行线分线段成比例定理得AH＝DH＝AD＝4，‎ ‎ ∴ OH＝OA－AH＝1．同理可得O1H＝7． ∴ 点O1的坐标为(1，7)．‎ ‎ ∵ BC⊥OC， ∴ OC为⊙O1的切线．‎ ‎ 又∵OP为⊙O1的切线， ∴ OC＝OP＝O1C＝O1P＝5．‎ ‎ ∴ 四边形OPO1C为正方形． ∴ ∠COP＝900． ∴ ∠POF＝∠OCD．‎ 第22题图 ‎ 又∵∠PFD＝∠ODC＝90°， ∴ △POF≌△OCD．‎ ‎∴ OF＝CD，PF＝OD． ∴ P(4，3)．‎ 设直线O1P的解析式为y＝kx+B(k≠0)．‎ 把O1(1，7)、P(4，3)分别代人y＝kx+B，‎ 得 解得 ‎∴ 直线O1P的解析式为y＝－x＋．‎ 若以PQ为直径的圆与⊙O1相切，则点Q为直线O1P与抛物线的交点，可设点Q的坐标为(m，n)，则有n＝－m＋，n＝m2－M ‎∴ －m＋＝m2－M．整理得m2＋3m－50＝0，‎ 解得m＝ ‎∴ 点Q的横坐标为或．‎ ‎4．（2010江苏无锡）如图，矩形ABCD的顶点A、B的坐标分别为（-4，0）和（2，0），BC=．设直线AC与直线x=4交于点E．‎ ‎（1）求以直线x=4为对称轴，且过C与原点O的抛物线的函数关系式，并说明此抛物线一定过点E；‎ ‎（2）设（1）中的抛物线与x轴的另一个交点为N，M是该抛物线上位于C、N之间的一动点，求△CMN面积的最大值．‎ ‎【答案】解：（1）点C的坐标．设抛物线的函数关系式为，‎ ‎ 则，解得 ‎∴所求抛物线的函数关系式为…………①‎ 设直线AC的函数关系式为则，解得．‎ ‎∴直线AC的函数关系式为，∴点E的坐标为 把x=4代入①式，得，∴此抛物线过E点．‎ ‎（2）（1）中抛物线与x轴的另一个交点为N（8，0），设M（x，y），过M作MG⊥x轴于G，则S△CMN=S△MNG+S梯形MGBC—S△CBN=‎ ‎=‎ ‎=‎ ‎∴当x=5时，S△CMN有最大值 ‎5．（2010湖南邵阳）如图（十四），抛物线y＝与x轴交于点A、B，与y轴相交于点C，顶点为点D，对称轴l与直线BC相交于点E，与x轴交于点F。‎ ‎（1）求直线BC的解析式；‎ ‎（2）设点P为该抛物线上的一个动点，以点P为圆心，r为半径作⊙P。‎ ‎①当点P运动到点D时，若⊙P与直线BC相交 ，求r的取值范围；‎ ‎②若r=，是否存在点P使⊙P与直线BC相切，若存在，请求出点P的坐标；若不存在，请说明理由．‎ 提示：抛物线y＝的顶点坐标，对称轴x＝.‎ ‎ 图（十四）‎ ‎【答案】解（1）令y=0，求得A点坐标为（－2，0），B点坐标为（6，0）；‎ 令x＝0，求得C点的坐标为（0，3）‎ 设BC直线为y＝kx＋b，把B、C点的坐标代入得： 解得k＝，b=3‎ 故BC的解析式为：y=x＋3‎ ‎（2）①过点D（2，4）作DG⊥BC于点G，因为抛物线的对称轴是直线x=2，所以点E的坐标为（2，2），所以有EF＝2，FB＝4，EB＝2，DE＝2，从图中可知，，所以有： 解得DG＝ 故当r＞，点P运动到点D时，⊙P与直线BC相交 ‎②由①知，直线BC上方的点D符合要求。设过点D并与直线BC平行的直线为y＝x＋n，把点D的坐标代入，求得n＝5，所以联立： 解得两点（2，4）为D点，（4，3）也符合条件。‎ 设在直线BC下方到直线BC的距离为的直线m与x轴交于点M，过点M作MN⊥BC于点N，所以MN=，又tan∠NBM＝　所以NB=，BM＝4，所以点M与点F重合。设直线m为y=x＋b 把点F的坐标，代入得：0＝×2＋b 得b=1，所以直线m的解析式为：y＝ｘ+１‎ 联立方程组：　　　解得：ｘ＝ ‎ 所以适合要求的点还有两点即（3－，）与（3＋，）‎ 故当r=，存在点P使⊙P与直线BC相切，符合条件的点P有四个，即是D ‎（2，4），（4，3）和（3－，），（3＋，）的坐标．‎ ‎6．（2010年上海）如图8，已知平面直角坐标系xOy，抛物线y＝－x2＋bx＋c过点A(4,0)、B(1,3) .‎ ‎（1）求该抛物线的表达式，并写出该抛物线的对称轴和顶点坐标；‎ ‎（2）记该抛物线的对称轴为直线l，设抛物线上的点P(m,n)在第四象限，点P关于直线l的对称点为E，点E关于y轴的对称点为F，若四边形OAPF的面积为20，求m、n的值.‎ 图8‎ ‎【答案】解：(1) 抛物线y＝－x2＋bx＋c过点 A(4,0)B(1,3).∴‎ ‎∴，，对称轴为直线，顶点坐标为 ‎（2）∵直线EP∥OA,E与P两点关于直线对称，∴OE=AP,∴梯形OEPA为等腰梯形，‎ ‎∴∠OEP=∠APE,∵OE=OF, ∴∠OEP=∠AFE,∴∠OFP=∠APE,∴OF∥AP,‎ ‎∴四边形OAPF为平行四边形，∵四边形OAPF的面积为20，∴，‎ ‎∴，∴.‎ ‎7．（2010重庆綦江县）已知抛物线y＝ax2＋bx＋c（a＞0）的图象经过点B（12,0）和C（0，－6），对称轴为x＝2．‎ ‎（1）求该抛物线的解析式；‎ ‎（2）点D在线段AB上且AD＝AC，若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动，同时另一动点Q以某一速度从C出发沿线段CB匀速运动，问是否存在某一时刻，使线段PQ被直线CD垂直平分？若存在，请求出此时的时间t（秒）和点Q的运动速度；若不存在，请说明理由；‎ ‎（3）在（2）的结论下，直线x＝1上是否存在点M使，△MPQ 为等腰三角形？若存在，请求出所有点M的坐标，若不存在，请说明理由．‎ ‎ 【答案】解：（1）方法一：∵抛物线过点C（0，－6）‎ ‎∴c＝－6，即y＝ax2 ＋bx－6‎ 由解得：，‎ ‎∴该抛物线的解析式为 方法二：∵A、B关于x＝2对称 ‎∴A（－8，0） 设 C在抛物线上，∴－6＝a×8×，即a＝‎ ‎∴该抛物线解析式为：‎ ‎（2）存在，设直线CD垂直平分PQ，‎ 在Rt△AOC中，AC＝＝10＝AD ‎∴点D在抛物线的对称轴上，连结DQ，如图：‎ 显然∠PDC＝∠QDC，‎ 由已知∠PDC＝∠ACD ‎∴∠QDC＝∠ACD，∴DQ∥AC DB＝AB－AD＝20－10＝10‎ ‎∴DQ为△ABC的中位线 ‎∴DQ＝AC＝5‎ AP＝AD－PD＝AD－DQ＝10－5＝5‎ ‎∴t＝5÷1＝5（秒）‎ ‎∴存在t＝5（秒）时，线段PQ被直线CD垂直平分 在Rt△BOC中，BC＝＝‎ ‎∴CQ＝‎ ‎∴点Q的运动速度为每秒单位长度．‎ ‎（3）存在．如图，‎ 过点Q作QH⊥x轴于H，则QH＝3，PH＝9‎ 在Rt△PQH中，PQ＝＝‎ ‎①当MP＝MQ，即M为顶点，‎ 设直线CD的直线方程为y＝kx＋b（k≠0），则：‎ ‎，解得：‎ ‎∴y＝3x－6‎ 当x＝1时，y＝－3‎ ‎∴M1(1，－3)‎ ‎②当PQ为等腰△MPQ的腰时，且P为顶点，‎ 设直线x＝1上存在点M（1，y），由勾股定理得：‎ ‎42＋y2＝90，即y＝±‎ ‎∴M2（1，）；M3（1，－）‎ ‎③当PQ为等腰△MPQ的腰时，且Q为顶点．‎ 过点Q作QE⊥y轴于E，交直线x＝1于F，则F（1，－3）‎ 设直线x＝1存在点M（1，y）由勾股定理得：‎ ‎，即y＝－3±‎ ‎∴M4（1，－3＋）；M5（1，－3－）‎ 综上所述，存在这样的五个点：M1(1，－3)；M2（1，）；M3（1，－）；M4（1，－3＋）；M5（1，－3－）‎ ‎8．（2010山东临沂）如图，二次函数的图象与轴交于,两点，且与轴交于点.‎ ‎（1）求该抛物线的解析式，并判断的形状；‎ ‎（2）在轴上方的抛物线上有一点,且以四点为顶点的四边形是等腰梯形，请直接写出点的坐标；‎ ‎（3）在此抛物线上是否存在点,使得以四点为顶点的四边形是直角梯形？若存在，求出点的坐标；若不存在，说明理由.‎ 第26题图 ‎【答案】解：根据题意，将A（,0）,B（2,0）代入y=-x2+ax+b中，‎ 得 解这个方程，得 全品中考网 所以抛物线的解析式为y=-x2+x+1.‎ 当x=0时，y=1.所以点C的坐标为（0，1）。‎ 所以在△AOC中，AC==.‎ 在△BOC中，BC==.‎ AB=OA+OB=.‎ 因为AC2+BC2=.‎ 所以△ABC是直角三角形。‎ 图1‎ ‎（2）点D的坐标是.‎ ‎（3）存在。‎ 由（1）知，AC⊥BC, ‎ ① 若以BC为底边，则BC∥AP,如图（1）所示，可求得直线BC的解析式为 ‎.‎ 直线AP可以看作是由直线AC平移得到的，所以设直线AP的解析式为，‎ 将A（,0）代入直线AP的解析式求得b=,所以直线AP的解析式为.‎ ‎ ‎ 因为点P既在抛物线上，又在直线AP上，所以点P的纵坐标相等，即-x2+x+1=.‎ 解得（不合题意，舍去）.‎ 图2 ‎ 当x=时，y=.‎ 所以点P的坐标为（，）.‎ ‎②若以AC为底边，则BP∥AC，如图（2）所示，可求得直线AC的解析式为 ‎.‎ 直线BP可以看作是由直线AC平移得到的，所以设直线BP的解析式为，‎ 将B（2,0）代入直线BP的解析式求得b=-4,所以直线BP的解析式为y=2x-4.‎ 因为点P既在抛物线上，又在直线BP上，所以点P的纵坐标相等，即-x2+x+1=2x-4‎ 解得（不合题意，舍去）.‎ 当x=-时，y=-9.‎ 所以点P的坐标为（-，-9）.‎ 综上所述，满足题目的点P的坐标为（，）或（-，-9）‎ ‎.9．（2010四川宜宾）将直角边长为6的等腰Rt△AOC放在如图所示的平面直角坐标系中，点O为坐标原点，点C、A分别在x、y轴的正半轴上，一条抛物线经过点A、C及点B(–3，0)．‎ ‎(1)求该抛物线的解析式；‎ ‎(2)若点P是线段BC上一动点，过点P作AB的平行线交AC于点E，连接AP，当 ‎△APE的面积最大时，求点P的坐标；‎ ‎(3)在第一象限内的该抛物线上是否存在点G，使△AGC的面积与（2）中△APE的最 大面积相等?若存在，请求出点G的坐标；若不存在，请说明理由．‎ ‎【答案】解：（1）由题意知：A（0，6），C（6，0），‎ 设经过点A、B、C的抛物线解析式为y=ax2+bx+c ‎24题图 则：‎ 解得：‎ ‎∴该抛物线的解析式为 ‎（2）如图：设点P（x，0），‎ ‎∵PE∥AB，∴△CPE∽△ABC，‎ ‎∴‎ 又∵S△ABC=BC×OA=27‎ ‎∴‎ ‎∴S△CPE==‎ S△ABP＝BP×OA=3x+9‎ 设△APE的面积为S 则S= S△ABC—S△ABP—S△CPE=‎ 当x=时，S最大值为 ‎∴点P的坐标为（，0）‎ ‎（3）假设存在点G（x，y），使△AGC的面积与（2）中△APE的最大面积相等．‎ 在（2）中，△APE的最大面积为，过点G做GF垂直y轴与点F．‎ ①当y＞6时，S△AGC=S梯形GFOC—S△GFA—S△AOC=（x+6）y—x（y-6）—×6×6‎ ‎=3x+3y-18‎ 即3x+3y-18=，‎ 又∵点G在抛物线上，，‎ ‎∴3x+3-18=‎ 解得：，当x=时，y=，当x=时，y=．‎ 又∵y＞6，∴‎ 点G的坐标为（，）‎ ②当y＜6时，如图：‎ S△AGC=S△GAF+S梯形GFOC—S△AOC=x（6—y）+-18=3x+3y-18‎ 即3x+3y-18=，‎ 又∵点G在抛物线上，，‎ ‎∴3x+3-18=‎ 解得：，当x=时，y=，当x=时，y=．‎ 又因为y＜6，所以点G的坐标为（，）．‎ 综和①②所述，点G的坐标为（，）和（，）．‎ ‎（3）解法2：可以向x轴作垂线，构成了如此下图的图形:‎ 则阴影部分的面积等于S△AGC=S△GCF+S梯形AGFO—S△AOC 下面的求解过程略．这样作可以避免了分类讨论．‎ ‎10．（2010 江苏连云港）（本题满分8分）已知反比例函数y＝的图象与二次函数y＝ax2＋x－1的图象相交于点（2，2）‎ ‎（1）求a和k的值；‎ ‎（2）反比例函数的图象是否经过二次函数图象的顶点，为什么？‎ ‎【答案】‎ ‎11．（2010 黄冈）（15分）已知抛物线顶点为C（1，1）且过原点O.过抛物线上一点P（x，y）向直线作垂线，垂足为M，连FM（如图）.‎ ‎（1）求字母a，b，c的值；‎ ‎（2）在直线x＝1上有一点，求以PM为底边的等腰三角形PFM的P点的坐标，并证明此时△PFM为正三角形；‎ ‎（3）对抛物线上任意一点P，是否总存在一点N（1，t），使PM＝PN恒成立，若存在请求出t值，若不存在请说明理由.‎ ‎【答案】（1）a＝－1，b＝2，c＝0‎ ‎（2）过P作直线x=1的垂线，可求P的纵坐标为，横坐标为.此时，MP＝MF＝PF＝1，故△MPF为正三角形.‎ ‎（3）不存在.因为当t＜，x＜1时，PM与PN不可能相等，同理，当t＞，x＞1时，PM与PN不可能相等.‎ ‎12．（2010 山东省德州） (已知二次函数的图象经过点A(3，0)，B(2，-3)，C(0，-3)．‎ ‎(1)求此函数的解析式及图象的对称轴；‎ x y O A B C P Q M N 第23题图 ‎(2)点P从B点出发以每秒0.1个单位的速度沿线段BC向C点运动，点Q从O点出发以相同的速度沿线段OA向A点运动，其中一个动点到达端点时，另一个也随之停止运动．设运动时间为t秒．‎ ‎①当t为何值时，四边形ABPQ为等腰梯形；‎ ‎②设PQ与对称轴的交点为M，过M点作 x轴的平行线交AB于点N，设四边形ANPQ 的面积为S，求面积S关于时间t的函数解析式，‎ 并指出t的取值范围；当t为何值时，‎ S有最大值或最小值．‎ ‎【答案】x y O A B C P Q D E G M N F 解：(1)∵二次函数的图象经过点C(0，-3)，‎ ‎∴c =-3．‎ 将点A(3，0)，B(2，-3)代入得 解得：a=1，b=-2．‎ ‎∴．‎ 配方得：，所以对称轴为x=1．‎ ‎(2) 由题意可知：BP= OQ=0.1t．‎ ‎∵点B，点C的纵坐标相等，‎ ‎∴BC∥OA．‎ 过点B，点P作BD⊥OA，PE⊥OA，垂足分别为D，E．‎ 要使四边形ABPQ为等腰梯形，只需PQ=AB．‎ 即QE=AD=1．‎ 又QE=OE－OQ=(2-0.1t)-0.1t=2-0.2t，‎ ‎∴2-0.2t=1．‎ 解得t=5．‎ 即t=5秒时，四边形ABPQ为等腰梯形．‎ ‎②设对称轴与BC，x轴的交点分别为F，G．‎ ‎∵对称轴x=1是线段BC的垂直平分线，‎ ‎∴BF=CF=OG=1．‎ 又∵BP=OQ，‎ ‎∴PF=QG．‎ 又∵∠PMF=∠QMG，‎ ‎∴△MFP≌△MGQ．‎ ‎∴MF=MG．‎ ‎∴点M为FG的中点 ‎ ‎∴S=，‎ ‎=．‎ 由=．‎ ‎．‎ ‎∴S=．‎ 又BC=2，OA=3，‎ ‎∴点P运动到点C时停止运动，需要20秒．‎ ‎∴0MN成立的x的取值范围。‎ ‎【答案】解：（1）∠ABE＝∠CBD=30° ‎ 在△ABE中，AB＝6‎ BC=BE=‎ CD=BCtan30°=4‎ ‎∴OD=OC-CD=2‎ ‎∴B(，6) D(0,2)‎ 设BD所在直线的函数解析式是y=kx+b ‎ ∴ ‎ 所以BD所在直线的函数解析式是 ‎(2)∵EF=EA=ABtan30°= ∠FEG=180°-∠FEB-∠AEB=60°‎ 又∵FG⊥OA ‎ ‎∴FG＝EFsin60°=3 GE=EFcos60°= OG=OA-AE-GE=‎ 又H为FG中点 ‎∴H（，） …………4分 ‎∵B(，6) 、 D(0,2)、 H（，）在抛物线图象上 ‎ ‎ ∴ ‎ ‎∴抛物线的解析式是 ‎(2)∵MP=‎ MN=6-‎ H=MP-MN=‎ 由得 该函数简图如图所示：‎ 当00，即HP>MN ‎15．（2010福建宁德）如图，在梯形ABCD中，AD∥BC，∠B＝90°，BC＝6，AD＝3，∠DCB＝30°.点E、F同时从B点出发，沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍，以EF为一边在CB的上方作等边△EFG．设E点移动距离为x（x＞0）.‎ ‎⑴△EFG的边长是____（用含有x的代数式表示），当x＝2时，点G的位置在_______；‎ ‎⑵若△EFG与梯形ABCD重叠部分面积是y，求 ‎①当0＜x≤2时，y与x之间的函数关系式；‎ ‎②当2＜x≤6时，y与x之间的函数关系式；‎ B E→ F→ C A D G ‎⑶探求⑵中得到的函数y在x取含何值时，存在最大值，并求出最大值.‎ ‎【答案】解：⑴ x，D点 ‎⑵ ①当0＜x≤2时，△EFG在梯形ABCD内部，所以y＝x2；‎ ‎②分两种情况：‎ Ⅰ.当2＜x＜3时，如图1，点E、点F在线段BC上，‎ ‎△EFG与梯形ABCD重叠部分为四边形EFNM，‎ ‎∵∠FNC＝∠FCN＝30°,∴FN＝FC＝6－2x.∴GN＝3x－6.‎ 由于在Rt△NMG中，∠G＝60°，‎ 所以，此时 y＝x2－（3x－6）2＝.‎ Ⅱ.当3≤x≤6时，如图2，点E在线段BC上，点F在射线CH上，‎ ‎△EFG与梯形ABCD重叠部分为△ECP，‎ ‎∵EC＝6－x,‎ ‎∴y＝（6－x）2＝.‎ ‎⑶当0＜x≤2时，∵y＝x2在x＞0时，y随x增大而增大，‎ ‎∴x＝2时，y最大＝；‎ 当2＜x＜3时，∵y＝在x＝时，y最大＝；‎ 当3≤x≤6时，∵y＝在x＜6时，y随x增大而减小，‎ ‎∴x＝3时，y最大＝.‎ B E C F A D G P H 图2‎ 综上所述：当x＝时，y最大＝.‎ B E F C A D G N M 图1‎ ‎16．（2010江西）如图，已知经过原点的抛物线y=-2x2+4x与x轴的另一交点为A，现将它向右平移m(m>0)个单位，所得抛物线与x轴交与C、D两点，与原抛物线交与点P.‎ ‎（1）求点A的坐标，并判断△PCA存在时它的形状（不要求说理）‎ ‎（2）在x轴上是否存在两条相等的线段，若存在，请一一找出，并写出它们的长度（可用含m的式子表示）；若不存在，请说明理由；‎ ‎（3）△CDP的面积为S，求S关于m的关系式。‎ x y D A C O P ‎【答案】解：（1）令-2x2+4x=0得x1=0，x2=2‎ ‎∴点A的坐标是（2，0），‎ ‎△PCA是等腰三角形，‎ ‎（2）存在。‎ OC=AD=m,OA=CD=2，‎ ‎（3）当02时，如图2‎ 作PH⊥x轴于H，设,‎ ‎∵A（2，0），C（m,0）,‎ ‎∴AC=m-2，∴AH=‎ ‎∴=OH= = ,‎ 把把=代入y=-2x2+4x，得 得, =‎ ‎∵CD=OA=2，‎ ‎∴．‎ ‎17．（2010 武汉 ）如图1，抛物线经过点A（－1，0），C（0，）两点，且与x轴的另一交点为点B．‎ ‎（1）求抛物线解析式； ‎ ‎（2）若抛物线的顶点为点M，点P为线段AB上一动点（不与B重合），Q在线段MB上移动，且∠MPQ=45°，设OP=x，MQ=，求于x的函数关系式，并且直接写出自变量的取值范围；‎ ‎（3）如图2，在同一平面直角坐标系中，若两条直线x=m，x=n分别与抛物线交于E、G两点，与（2）中的函数图像交于F、H两点，问四边形EFHG能否为平行四边形？若能，求出m、n之间的数量关系；若不能，请说明理由．‎ 图 1‎ 图 2‎ ‎25．【答案】（1）；‎ ‎（2）由顶点M（1，2）知∠PBM=45°，易证△MBP∽△MPQ得 ‎，得，即；‎ ‎（3）存在，设点E、G是抛物线分别与直线x=m，x=n的交点，则、，同理、，．由四边形EFHG为平行四边形得EG=FH，即，由，因此，四边形EFHG可以为平行四边形，m、n之间的数量关系是m+n=2（0≤m≤2，且m≠1）．‎ ‎18．（2010四川 巴中）如图12已知△ABC中，∠ACB＝90°以AB 所在直线为x 轴，过c 点的直线为y 轴建立平面直角坐标系．此时，A 点坐标为（一1 ， 0）， B 点坐标为（4，0 ） ‎ ‎（1）试求点C 的坐标 ‎（2）若抛物线过△ABC的三个顶点，求抛物线的解析式．‎ ‎（3）点D（ 1，m ）在抛物线上，过点A 的直线y=－x－1 交（2）中的抛物线于点E，那么在x轴上点B 的左侧是否存在点P，使以P、B、D为顶点的三角形与△ABE 相似？若存在，求出P点坐标；若不存在，说明理由。‎ D G H ‎【答案】（1）∵∠ACB＝90°，CO⊥AB，△ACO∽△CBO，∴，CO=2，‎ 则C（0，2）；‎ ‎（2）抛物线过△ABC的三个顶点，则，∴，抛物线的解析式为；‎ ‎（3）点D（ 1，m ）在抛物线上，，∴D（1，3），把直线y=－x－1与抛物线联立成方程组∴，‎ ‎∴E（5，－6）,过点D作DH垂直于x轴,过点E作EG垂直于x轴,DH=BH=3,∴∠DBH=45°,‎ BD=,AG=EG=6, ∴∠EAG=45°,AE=,‎ 当P在B的右侧时,∠DBP=135°≠∠ABE,两个三角形不相似,所以P点不存在；‎ 当P 在B的左侧时 ⅰ) △DPB∽△EBA时，，，∴P的坐标为（，0），‎ ⅱ) △DPB∽△BEA时， ，，∴P的坐标为（，0），‎ 所以点P的坐标为（，0）或（，0）。‎ ‎19．（2010浙江湖州）如图，已知在直角梯形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA＝AB＝2，OC＝3，过点B作BD⊥BC，交OA于点D，将∠DBC绕点B按顺时针方向旋转，角的两边分别交y轴的正半轴于E和F．‎ ‎（1）求经过A，B，C三点的抛物线的解析式；‎ ‎（2）当BE经过（1）中抛物线的顶点时，求CF的长；‎ ‎（3）连接EF，设△BEF与△BFC的面积之差为S，问：当CF为何值时 S最小，并求出这个最小值.‎ ‎ ‎ ‎．‎ ‎【答案】由题意得：A（0，2）、B（2，2）、C（3，0），设经过A，B，C 三点的抛物线的解析式为，则，解得：，所以．‎ ‎（2）由＝，所以顶点坐标为G（1，），过G作GH⊥AB，垂足为H，则AH＝BH＝1，GH＝－2＝，∵EA⊥AB，GH⊥AB，∴EA∥GH，∴GH是△BEA的中位线，∴EA＝3GH＝，过B作BM⊥OC，垂足为M，则MB＝OA＝AB，∵∠EBF＝∠ABM＝90°，∴∠EBA＝∠FBM＝90°－∠ABF，∴R t△EBA≌R t△FBM，∴FM＝EA＝，∵CM＝OC－OM＝3－2＝1，∴CF＝FM＋CM＝．‎ ‎（3）设CF＝a，则FM＝ a－1或1－ a，∴BF2＝FM2＋BM2＝(a－1)2＋22＝a2－2a＋5，又∵△EBA≌△FBM，∴BM＝BF，‎ 则，又，‎ ‎∴S＝ ，即S＝，∴当a＝2（在2＜a＜3）时，．‎ ‎20．（2010江苏常州）如图，已知二次函数的图像与轴相交于点A、C，与轴相较于点B，A（），且△AOB∽△BOC。‎ ‎（1）求C点坐标、∠ABC的度数及二次函数的关系是；‎ ‎（2）在线段AC上是否存在点M（）。使得以线段BM为直径的圆与边BC交于P点（与点B不同），且以点P、C、O为顶点的三角形是等腰三角形？若存在，求出的值；若不存在，请说明理由。‎ ‎【答案】‎ ‎21．（2010江苏常州）如图，在矩形ABCD中，AB=8，AD=6，点P、Q分别是AB边和CD边上的动点，点P从点A向点B运动，点Q从点C向点D运动，且保持AP-CQ。设AP=‎ ‎（1）当PQ∥AD时，求的值；‎ ‎（2）当线段PQ的垂直平分线与BC边相交时，求的取值范围；‎ ‎（3）当线段PQ的垂直平分线与BC相交时，设交点为E，连接EP、EQ，设△EPQ的面积为S，求S关于的函数关系式，并写出S的取值范围。‎ ‎【答案】‎ ‎22．（2010 山东滨州）如图，四边形ABCD是菱形，点D的坐标是，以点C为顶点的抛物线 恰好经过轴上A、B两点．‎ ‎(1)求A、B、C三点的坐标；‎ ‎(2) 求经过A、B、C三点的的抛物线的解析式；‎ ‎(3)若将上述抛物线沿其对称轴向上平移后恰好过D点，求平移后抛物线的解析式，并指出平移了多少各单位？‎ ‎【答案】解：(1)由抛物线的对称性可知AM=BM．‎ 在Rt△AOD和Rt△BMC中，‎ ‎∵OD=MC，AD=BC，‎ ‎∴△AOD≌△BMC ‎∴OA=MB=MA分 设菱形的边长为2m，在Rt△AOD中，‎ ‎，解得．‎ ‎∴DC=2，OA=1，OB=3．‎ ‎∴A、B、C三点的坐标分别为、、‎ ‎(2)设抛物线的解析式为，带入A点的坐标，得 ‎∴抛物线的解析式为 ‎(3) 设抛物线的解析式为，代入D点的坐标，得 ‎∴平移后的抛物线的解析式为 ‎∴平移了个单位．‎ ‎23．（2010湖北荆门）已知一次函数y＝的图象与x轴交于点A．与轴交于点；二次函数图象与一次函数y＝的图象交于、两点，与轴交于、两点且点的坐标为 ‎（1）求二次函数的解析式；‎ ‎（2）求四边形BDEF的面积S；‎ ‎（3）在轴上是否存在点P，使得△是以为直角顶点的直角三角形？若存在，求出所有的点，若不存在，请说明理由。‎ ‎【答案】解：（1）∵ 由题意知:当x=0时,y=1, ∴B（0，1）,当y=0时,x=－2, ∴A（－2，0）‎ ‎∴解得,所以 ‎（2）当y=0时, ,解得x1=1,x2=2, ∴D(1,0) E(2,0) ∴AO=3,AE=4. S=S△CAE－S△ABD，S=，S=4.5,‎ ‎ (3)存在点P(a,0),当P为直角顶点时,如图,过C作CF⊥x轴于F, ∵Rt△BOP∽Rt△PFC,‎ 由题意得，AD＝6，OD＝1，易知，AD∥BE，‎ ‎∴．即,整理得:a2－4a－3=0,解得a=1或a=3,所以所求P点坐标为(1,0)或(3,0).综上所述,满足条件的点P有两个.‎ ‎24．（2010 湖南株洲）（本题满分10分）在平面直角坐标系中，抛物线过原点O，且与轴交于另一点，其顶点为．孔明同学用一把宽为带刻度的矩形直尺对抛物线进行如下测量：‎ ‎① 量得；‎ ‎② 把直尺的左边与抛物线的对称轴重合，使得直尺左下端点与抛物线的顶点重合（如图1），测得抛物线与直尺右边的交点的刻度读数为．‎ 请完成下列问题：‎ ‎（1）写出抛物线的对称轴；‎ ‎（2）求抛物线的解析式；‎ ‎（3）将图中的直尺（足够长）沿水平方向向右平移到点的右边（如图2），直尺的两边交 轴于点、，交抛物线于点、．求证：．‎ 图1‎ 图2‎ ‎·‎ B ‎【答案】（1）　　　　　　　　　　　　　　　　　　　　　　　　　　　‎ ‎（2）设抛物线的解析式为：，当时，，即；当时，，即，依题意得：，解得：．‎ ‎∴抛物线的解析式为：． ‎ ‎（3）方法一：过点作，垂足为，设， ，得： ①‎ ‎ ②‎ 又，得，分别代入①、②得：，‎ ‎∴‎ 得：‎ 又 ‎∴ ‎ 方法二：过点作，垂足为，设，则，得：‎ ‎ ∵ ‎ ‎∴‎ ‎25．（2010 四川成都）在平面直角坐标系中，抛物线与轴交于两点（点在点的左侧），与轴交于点，点的坐标为，若将经过两点的直线沿轴向下平移3个单位后恰好经过原点，且抛物线的对称轴是直线．‎ ‎（1）求直线及抛物线的函数表达式；‎ ‎（2）如果P是线段上一点，设、的面积分别为、，且，求点P的坐标；‎ ‎（3）设⊙Q的半径为l，圆心在抛物线上运动，则在运动过程中是否存在⊙Q与坐标轴相切的情况？若存在，求出圆心的坐标；若不存在，请说明理由．并探究：若设⊙Q的半径为，圆心在抛物线上运动，则当取何值时，⊙Q与两坐轴同时相切？‎ ‎【答案】（1）解：（1）∵沿轴向下平移3个单位后恰好经过原点，‎ ‎ ∴，。‎ ‎ 将 代入，得。解得。‎ ‎ ∴直线AC的函数表达式为。‎ ‎ ∵抛物线的对称轴是直线 ‎∴解得 ‎∴抛物线的函数表达式为。‎ ‎（2）如图，过点B作BD⊥AC于点D。‎ ‎ ‎ ‎∵，‎ ‎∴ ‎ ‎∴。‎ 过点P作PE⊥x轴于点E，‎ ‎∵PE∥CO，∴△APE∽△ACO，‎ ‎∴，‎ ‎∴‎ ‎∴，解得 ‎∴点P的坐标为 ‎（3）（Ⅰ）假设⊙Q在运动过程中，存在与坐标轴相切的情况。‎ ‎ 设点Q的坐标为。‎ ① 当⊙Q与y轴相切时，有，即。‎ 当时，得，∴‎ 当时，得，∴‎ ② 当⊙Q与x轴相切时，有，即 当时，得，即，解得，∴‎ 当时，得，即，解得，∴，。‎ 综上所述，存在符合条件的⊙Q，其圆心Q的坐标分别为，，，，。‎ ‎（Ⅱ）设点Q的坐标为。‎ 当⊙Q与两坐标轴同时相切时，有。‎ 由，得，即，‎ ‎∵△=‎ ‎∴此方程无解。‎ 由，得，即，‎ 解得 ‎∴当⊙Q的半径时，⊙Q与两坐标轴同时相切。‎ ‎26．（2010山东潍坊）如图所示，抛物线与x轴交于A（－1，0）、B（3，0）两点，与y轴交于C（0，－3）．以AB为直径做⊙M，过抛物线上的一点P作⊙M的切线PD，切点为D，并与⊙M的切线AE相交于点E．连接DM并延长交⊙M于点N，连接AN．‎ ‎（1）求抛物线所对应的函数的解析式及抛物线的顶点坐标；‎ ‎（2）若四边形EAMD的面积为4，求直线PD的函数关系式；‎ ‎（3）抛物线上是否存在点P，使得四边形EAMD的面积等于△DAN的面积？若存在，求出点P的坐标，若不存在，说明理由．‎ ‎【答案】解：（1）因为抛物线与x轴交于点A（－1，0）、B（3，0）两点，设抛物线的函数关系式为y＝a（x＋1）（x－3），∵抛物线与y轴交于C（0，－3），∴－3＝ a（0＋1）（0－3），解得a＝1，所以抛物线的解析式为y＝x2－2x－3＝（x－1）2－4，因此抛物线的顶点坐标为（1，－4）；‎ ‎（2）连接EM，∵EA、ED是⊙M的切线，∴EA＝ED，EA⊥AM，ED⊥MD，∴△EAM≌△EDM，又四边形EAMD的面积为4，∴S△EAM＝2，∴AM·AE＝2，又AM＝2，∴AE＝2，因此E1（－1，2）或者E2（－1，－2），当点E在第二象限时，切点D在第一象限，在 Rt△EAM中，tan∠EMA＝，故∠EMA＝60°，∴∠DMB＝60°，过切点D作DF⊥AB于F点，∴MF＝1，DF＝，则直线PD过E（－1，2）、D（2， ）的坐标代入，则函数PD的解析式为y＝－．当点E在第三象限时，切点D在第四象限，同理可求直线PD的解析式为y＝，因此直线PD的函数关系式为y＝－或y＝；‎ ‎（3）若四边形EAMD的面积等于△DAN的面积，又S四边形EAMD＝2S△EAM，S△DAN＝2S△AMD，则S△EAM＝ S△AMD，∴E、D两点到x轴的距离相等，∵PD与⊙M相切，∴点D与点E在x轴同侧，∴切线PD与x轴平行，此时切线PD的函数关系式为y＝2或y ‎＝－2，当y＝2时，由y＝ x2－2x－3得，x＝1±，当y＝－2时，由y＝ x2－2x－3得，x＝1±，故满足条件点P的位置有4个，分别是P1（1＋，2）、P2（1－，2）、P3（1＋，－2）、P4（1－，－2）．‎ ‎27．（2010广东中山）已知二次函数的图象如图所示，它与x轴的一个交点坐标为（-1，0），与y轴的交点坐标为（0，3）．‎ ‎（1）求出b，c的值，并写出此二次函数的解析式；‎ ‎（2）根据图象，写出函数值y为正数时，自变量x的取值范围．‎ ‎【答案】解：（1）把（-1，0），（0，3）分别代入，‎ 得 ，解得 所以，‎ ‎（2）令y=0，得 解得，‎ 所以，由图象可知，函数值y为正数时，自变量x的取值范围是 -1＜x＜3．‎