全国各地500套中考数学试题分类汇编 直线与圆的位置关系2 71页

‎2011中考模拟分类汇编：直线与圆的位置关系 一、选择题 ‎1、（2011年北京四中中考模拟19）如图，PA为⊙O的切线，A为切点，PO交⊙O于点B，PA＝8，OA＝6，则tan∠APO的值为（ ）‎ A、 B、 C、 D、‎ ‎2、（2011年北京四中模拟26）‎ 如果等边三角形的边长为6，那么它的内切圆的半径为 （ ）‎ ‎ A．3 B． C． D．‎ 答案：B ‎3.（2011.河北廊坊安次区一模）一个钢管放在V形架内，图3是其截面图，O为钢管的圆心．如果钢管的半径为‎25 Cm，∠MPN = 60°，则OP 的长为 A．‎50 Cm B．‎25Cm C．Cm D．‎50Cm 答案:A ‎4.(2011湖北省天门市一模)如图，在中，，，，经过点且与边相切的动圆 与分别相交于点，则线段长度的最小值是（ ）‎ A． B． C． D．‎ ‎（第4题）‎ 答案:B A G B H C F D E 第5题 ‎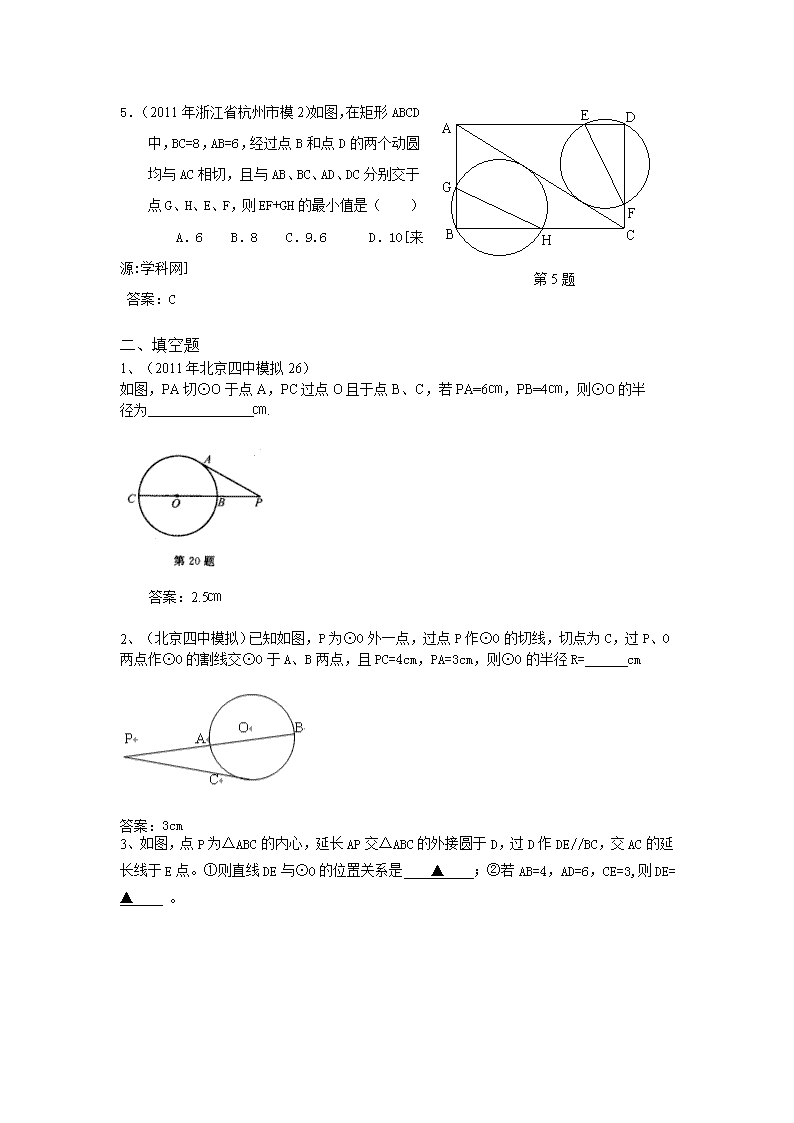5．（2011年浙江省杭州市模2）如图，在矩形ABCD中，BC=8，AB=6，经过点B和点D的两个动圆均与AC相切，且与AB、BC、AD、DC分别交于点G、H、E、F，则EF+GH的最小值是（ ）‎ A．6 B．‎8 ‎C．9.6 D．10[来源:学科网]‎ 答案：C 二、填空题 ‎1、（2011年北京四中模拟26）‎ 如图，PA切⊙O于点A，PC过点O且于点B、C，若PA=6㎝，PB=4㎝，则⊙O的半 径为 ㎝.‎ 答案：2.5㎝ ‎2、（北京四中模拟）已知如图，P为⊙O外一点，过点P作⊙O的切线，切点为C，过P、O两点作⊙O的割线交⊙O于A、B两点，且PC=‎4cm，PA=‎3cm，则⊙O的半径R= cm 答案：‎3cm ‎ ‎3、如图，点P为△ABC的内心，延长AP交△ABC的外接圆于D，过D作DE//BC，交AC的延长线于E点。①则直线DE与⊙O的位置关系是 ▲ ；②若AB=4，AD=6，CE=3,则DE= ▲ 。 ‎ 答案：相切， ‎ ‎4．（ 2011年杭州三月月考）如图所示，在中，，，若以为圆心，为半径所得的圆与斜边只有一个公共点，则的取值范围是： ▲ 。‎ 答案：或 B C D A ‎（第5题图）‎ ‎5. （2011年海宁市盐官片一模）如图、是的两条弦，=30°，过点的切线与的延长线交于点，则的度数为 ． ‎ 答案：30°‎ ‎6、（2011年北京四中34模）在直径为12的⊙O中，点M为⊙O所在平面上一点，且OM=5，则过点M的⊙O最短的弦长是 ‎ 答案：‎ ‎7．（2011杭州市模拟）如图，矩形纸片ABCD，点E是AB上一点，且BE∶EA=5∶3，EC=，把△BCE沿折痕EC向上翻折，若点B恰好落在AD边上，设这个点为F，则（1）AB= ，BC= ；（2）若⊙O内切于以F、E、B、C为顶点的四边形，则⊙O的面积= ．‎ A EA CA BA DA OA ‎（第7题图）‎ FA ‎；‎ 答案：AB=24，BC=30，⊙O的面积=100．（1+1+2分）‎ ‎8. （2011广东南塘二模）Rt△ABC中，∠C＝90°，AC＝4，BC＝3，内切圆半径＝ ；‎ 答案：1‎ ‎9.（浙江杭州靖江2011模拟）如图，AB是半图的直径，C为BA延长线上的一点，CD切半圆于点E。已知OA＝1，设DF＝x，AC＝y，则y关于x的函数解析式是_____________。（根据2009年衢州中考试卷改编）‎ 答案：‎ ‎10.（浙江杭州进化2011一模）如图，⊙O1和⊙O2的半径为2和3，连接O1O2，交⊙O2于点P，O1O2=7，若将⊙O1绕点按顺时针方向以30°/秒的速度旋转一周，请写出⊙O1与⊙O2相切时的旋转时间为_______秒．‎ 答案：3或6或9‎ E M N O C B A F 第11题 ‎11、（2011杭州模拟20）如图，AB是半圆O的直径，C为半圆上一点，N是线段BC上一点（不与B﹑C重合），过N作AB的垂线交AB于M，交AC的延长线于E，过C点作半圆O的切线交EM于F，若NC∶CF＝3∶2，则 sinB=_______．‎ 答案：‎ ‎12、（江西省九校2010—2011第一次联考）如图，某房间一角（AC⊥BC）‎ 放有一张直径为‎2m的圆桌（桌面紧贴AC、BC两边）,则图中阴影部分的面积 是 ．21世纪教育网 A 第13题 O C B 答案：　1－‎ ‎13、（江西省九校2010—2011第一次联考）如图，Rt△ABC中∠C=90°、∠A=30°，‎ 在AC边上取点O画圆使⊙O经过A、B两点，下列结论正确的序号是 [来源:Zxxk.Com]‎ ‎(多填或错填得0分,少填酌情给分) ．‎ ①AO=2CO ； ②AO=BC ； ③以O为圆心，以OC为半径的圆与AB相切；‎ ‎ ④延长BC交⊙O与D，则A、B、D是⊙O的三等分点．‎ 答案：①③④‎ ‎14、（北京四中2011中考模拟13）如图：⊙O与AB相切于点A，BO与⊙O交 于点C，，则等于 .‎ 答案：‎ ‎21世纪教育网 ‎15、（北京四中2011中考模拟14）已知圆的直径为13㎝,圆心到直线L的距离为6㎝,那么直线L和这个圆的公共点的个数为_________________.‎ 答案：2个 三、解答题[来源:学§科§网Z§X§X§K]‎ ‎1．（2011年黄冈中考调研六）（满分7分）如图，从⊙O外一点A作⊙O的切线AB、AC，切点分别为B、C，且⊙O直经BD=6，连结CD、AO。‎ ‎（1）求证：CD∥AO；‎ ‎(2)∵CD∥AO ‎∴∠3=∠4‎ ‎∵AB是⊙O的切线，DB是直径 ‎∴∠DCB=∠ABO=90O ‎∴△BDC∽△AOB ‎ ‎∴= ‎∴= ‎∴y = ‎ ∴018，所以渔船A不会进入海洋生物保护区． ‎ A B O F ‎ E ‎ D C ‎15.（2010年浙江杭州）已知：如图，AB是⊙O的直径，点C、D为圆上两点，且弧CB＝弧CD，CF⊥AB于点F，CE⊥AD的延长线于点E．‎ ‎ （1）试说明：DE＝BF；‎ ‎ （2）若∠DAB＝60°，AB＝6，求△ACD的面积．‎ ‎ （1）∵ 弧CB=弧CD ‎∴ CB=CD，∠CAE=∠CAB 又∵ CF⊥AB，CE⊥AD ‎∴ CE=CF ‎∴ △CED≌△CFB ‎∴ DE=BF ‎（2）易得：△CAE≌△CAF[来源:学科网]‎ 易求：‎ ‎∴ ‎ x y O P A ‎-2‎ ‎16.（2010年江西南昌一模）如图，在平面直角坐标系中，，直线OA与轴的夹角为，以P为圆心， 为半径作⊙P,与交于点.‎ (1) 当r为何值时，△为等边三角形？‎ (2) 当⊙P与直线相切时,求的值.‎ 答案：（1）作于M.‎ ‎∵是等边三角形,‎ ‎∴‎ ‎∵‎ ‎∴‎ x y O P A ‎-2‎ C M ‎∴‎ ‎∴‎ ‎(2)连结 ‎∵与直线相切,‎ ‎∴⊙P的半径为4+2=6.‎ ‎∴‎ 则 ‎∵‎ ‎∴‎ ‎[来源:学,科,网Z,X,X,K]‎ ‎17.(2010年厦门湖里模拟) 如图，已知在⊙O中，AB=4，AC是⊙O的直径，AC⊥BD于F，∠A=30°.[来源:学。科。网]‎ ‎（1）求图中阴影部分的面积；‎ A B D O F C ‎（2）若用阴影扇形OBD围成一个圆锥侧面，请求出这个圆锥的底面圆的半径.‎ 答案：（1）∵∠A=30° AC⊥BD ‎ ‎∴BF= ∠BOC=∠COD=60° OB=2OF ‎∴OF=2，OB=4‎ S阴= ‎ ‎（2）根据题意得: ∴= ‎ ‎18.(2010年厦门湖里模拟)如图，已知AB是⊙O的直径，点C在⊙O上，P是△OAC的重心，且OP＝，∠A＝30º．‎ A O B D C P ‎(1)求劣弧的长；‎ ‎(2)若∠ABD＝120º，BD＝1，求证：CD是⊙O的切线．‎ 答案：.(1)解：延长OP交AC于E，[来源:学,科,网Z,X,X,K]‎ ‎ ∵ P是△OAC的重心，OP＝，‎ ‎ ∴ OE＝1， ‎ ‎ 且 E是AC的中点.‎ ‎ ∵ OA＝OC，∴ OE⊥AC.‎ ‎ 在Rt△OAE中，∵ ∠A＝30°，OE＝1，‎ ‎ ∴ OA＝2. ‎ ‎ ∴ ∠AOE＝60°. ‎ ‎ ∴ ∠AOC＝120°. ‎ ‎ ∴ ＝π. ‎ ‎(2)证明：连结BC.‎ ‎ ∵ E、O分别是线段AC、AB的中点，‎ ‎ ∴ BC∥OE，且BC＝2OE＝2＝OB＝OC. ‎ ‎ ∴ △OBC是等边三角形. ‎ 法1：∴ ∠OBC＝60°.‎ ‎ ∵ ∠OBD＝120°，∴ ∠CBD＝60°＝∠AOE. ‎ ‎∵ BD＝1＝OE，BC＝OA，‎ ‎ ∴ △OAE ≌△BCD. ‎ ‎ ∴ ∠BCD＝30°.‎ ‎ ∵ ∠OCB＝60°，‎ ‎ ∴ ∠OCD＝90°. ‎ ‎ ∴ CD是⊙O的切线. ‎ ‎ 法2：过B作BF∥DC交CO于F.‎ ‎ ∵ ∠BOC＝60°，∠ABD＝120°,‎ ‎ ∴ OC∥BD. ‎ ‎ ∴ 四边形BDCF是平行四边形. ‎ ‎ ∴ CF＝BD＝1.‎ ‎ ∵ OC＝2，[来源:学科网ZXXK]‎ ‎ ∴ F是OC的中点.‎ ‎ ∴ BF⊥OC. ‎ ‎ ∴ CD⊥OC. ‎ ‎ ∴ CD是⊙O的切线. ‎ ‎19.（2010年天水模拟）如图，AB是⊙O是直径，过A作⊙O的切线，在切线上截取AC=AB，连结OC交⊙O于D，连结BD并延长交AC于E，⊙F是△ADE的外接圆，⊙F在AE上.‎ 求证：（1）CD是⊙F的切线；‎ ‎（2）CD=AE.‎ 证明：（1）连接DF ‎∵CA 切⊙O于A，∴∠CAB=90°‎ 又∵∠OAD=∠ODA ∠FAD=∠FDA ‎∴∠OAC=∠ODF=90°‎ ‎∴∠FDC=90‎ ‎∴CD是⊙F的切线 ‎（2）FDC=DAC=90‎ ‎∠C=∠C ‎∴△CDF∽△CAO 又∵AC=AB ‎∴==‎ 又∵DF=FE AE=2DF ‎∴AE=CD ‎20．（2010年广州中考数学模拟试题一）如图①②，图①是一个小朋友玩“滚铁环”的游戏，铁环是圆形的，铁环向前滚动时，铁环钩保持与铁环相切.将这个游戏抽象为数学问题，如图②.已知铁环的半径为5个单位（每个单位为‎5cm），设铁环中心为O，铁环钩与铁环相切点为M，铁环与地面接触点为A，∠MOA＝α，且sinα＝.‎ ‎（1）求点M离地面AC的高度BM（单位：厘米）；‎ ‎（2）设人站立点C与点A的水平距离AC 等于11个单位，求铁环钩MF的长度（单位：厘米）.‎ A B M O F C ‎②‎ ‎①‎ H N 第20题图 答案：过M作AC平行的直线，与OA，FC分别相交于H，N.‎ ‎（1）在Rt△OHM中，∠OHM＝90°，OM＝5，HM＝OM×sinα＝3，所以OH＝4，MB＝HA＝5－4＝1（单位），1×5＝5（cm），所以铁环钩离地面的高度为‎5cm.‎ ‎（2）因为∠MOH+∠OMH＝∠OMH+∠FMN＝90°，∠FMN＝∠MOH＝α，所以＝sinα＝，即得FN＝FM，在Rt△FMN中，∠FNM＝90°，MN＝BC＝AC－AB＝11－3＝8（单位），由勾股定理FM2＝FN2+MN2，即FM2＝(FM)2+82，解得FM＝10（单位），10×5＝50（cm），所以铁环钩的长度FM为‎50cm.‎ 直线与圆的位置关系 A组 一 选择题 ‎1、（2011双柏县中考模拟）如图，PA、PB分别切⊙O于点A、B，点E是⊙O上一点，且∠AEB=60°，则∠P的度数为( )‎ P E A B ‎60°‎ O A．120° B.90° C.60° D.75°‎ ‎【答案】C ‎2、(2011宁波江北模拟) 如图，∠ACB＝60○，半径为2的⊙0切BC于点C，若将⊙O在CB上向右滚动，则当滚动到⊙O与CA也相切时，圆心O移动的水平距离为 （　　　）‎ A．2π B．4π 　　　 C． 　　D．4‎ 考查内容：‎ 答案：C ‎3、(2011宁波江北模拟) 如图，⊙O是⊿ABC的外接圆，已知AD平分∠BAC交⊙O于点D，AD=5，BD=2，则DE的长为（ ） ‎ ‎ A． B． C． D． ‎ ‎[来源:Z§xx§k.Com]‎ ‎[来源:Z.xx.k.Com]‎ ‎ 考查内容：‎ 答案：D ‎4（2011广州六校一摸）已知的半径为，如果圆心到直线的距离为，那么直线和的位置关系是（　　）‎ Ａ．相交 Ｂ．相切 Ｃ．相离 Ｄ．相交或相离 答案:C.‎ 二 填空题 ‎1．（南京市溧水县2011年中考一模）‎ 如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连结BC．若∠A＝36°，则∠C= ▲ ．‎ ‎（第1题）‎ O C B A 答案：27°‎ ‎1、(2011平顶山二模) 如图，⊙0内切于△ABC，切点分别为D、E、F. 已知＜B=50°，＜C=60°，连结OE、OF、DE、DF.则＜EDF= 度.‎ 考查内容: ‎ 答案：55‎ 三 解答题 ‎1．(2011杭州市金山学校中考模拟) (6分) （根据2011年3月杭州市九年级数学月考试题第 ‎21题改编）‎ 如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.‎ ‎(1)尺规作图：过A，D，C三点作⊙O（只要求作出图形，保留痕迹，不要求写作法）；‎ ‎(2)求证：BC是过A，D，C三点的圆的切线；‎ ‎【答案】（ 6分）‎ 解：（1）作出圆心O， ………………………………………………………………2分 以点O为圆心，OA长为半径作圆.…………………………………………1分 ‎（2）证明：∵CD⊥AC,∴∠ACD=90°. ‎ ‎∴AD是⊙O的直径……………1分 连结OC，∵∠A=∠B=30°,‎ ‎∴∠ACB=120°,又∵OA=OC, ‎ ‎∴∠ACO=∠A =30°,…………1分 ‎∴∠BCO=∠ACB-∠ACO =120°-30°=90°. ‎ ‎∴BC⊥OC,‎ ‎∴BC是⊙O的切线. ……………………………………………1分 ‎2. （2011萧山区中考模拟）【改编】（本小题满分8分）‎ ‎ “‎6”‎字形图中，FM是大⊙O的直径，BC与大⊙O相切于B，‎ OB与小⊙O相交于点A，AD∥BC，CD∥BH∥FM，DH⊥BH于H，‎ 设∠FOB＝α，OB＝4，BC＝6．‎ ‎（1）求证：AD为小⊙O的切线；‎ 第21题 ‎（2）在图中找出一个可用α表示的角，并说明你这样表示的理由；（根据所写结果的正确性及所需推理过程的难易程度得分略有差异）‎ ‎（3）当α＝30º时，求DH的长。（结果保留根号)‎ ‎ ‎ ‎【答案】（1）证明：∵是大⊙O的切线，‎ ‎ ∴∠＝90°. ‎ ‎ ∵∥, ‎ ‎ ∴∠OAD＝90°.即⊥. ‎ ‎ 又 ∵点A在小⊙O上，‎ ‎ ∴AD是小⊙O的切线. ………………………………3分 ‎(2)答案不唯一，略。 …………………………1分 ‎ (3)∵∥，∥,‎ ‎ ∴四边形是平行四边形. ‎ ‎ ∴. …………………………………2分 ‎ ∵∥，∴.‎ ‎ ∴.‎ ‎ 又∵,‎ ‎ ∴.…………………………………………2分 ‎②‎ ‎①‎ ‎③‎ P ‎④‎ ‎3．（2011浙江新昌县模拟）图①是一个小朋友玩“滚铁环”的游戏，将这个游戏抽象为数学问题如图②，已知铁环的半径为‎25cm，设铁环中心为，铁环与地面接触点为，铁环钩与铁环的接触点为，铁环钩与手的接触点是，铁环钩长‎75cm, 表示点距离地面的高度.‎ ‎[来源:Zxxk.Com]‎ ‎ (1)当铁环钩与铁环相切时(如图③)，切点离地面的高度为‎5cm，求水平距离 的长；‎ ‎(2)当点与点同一水平高度时(如图④)，铁环容易向前滚动，现将如图③铁环钩的一端从点提升到与点同一水平高度的点，铁环钩的另一端点从点上升到点，且水平距离保持不变，求的长（精确到‎1cm）.‎ ‎【答案】解:（1）如图四边形，是矩形，‎ ‎ 中， 2分 方法一 ∵是圆的切线，∴‎ ‎∴,‎ 得,又, ∴ ‎ P ‎∽△AIB,得 即得 2分 ‎ (cm) 1分 方法二：∵是圆的切线，∴‎ ‎∴,‎ 得,∴‎ 中， 2分 ‎（cm） 1分 ‎(2)如图3，四边形是矩形，‎ ‎ 1分 中;‎ 中, 2分 ‎,[来源:学。科。网]‎ ‎() 2分 ‎4．（南京市雨花台2011年中考一模）(8分)如图，四边形是平行四边形，以AB为直径的⊙O经过点D，点E是⊙O上一点，且∠AED=45°。‎ ‎（1）试判断CD与⊙O的位置关系，并说明理由;‎ ‎（2）若⊙O 的半径为，，求∠ADE的正弦值．‎ ‎ ‎ ‎（第2题）‎ 答案：（1）与相切。…………………1分 理由是：连接，‎ 则 ‎∵四边形是平行四边形，‎ ‎∴∥‎ ‎∴‎ ‎∴ ∴与相切。………………4分 ‎（2）连接，则，‎ ‎∵是的直径，‎ ‎∴，……………………6分 在△中 ，。‎ ‎ ∴ ………………………………8分 ‎（其它解法，正确合理可参照给分。）‎ ‎5.（南京市玄武区2011年中考一模）（7分） 如图，AB为⊙O的直径，点C在上，点D在AB的延长线上于，且AC=CD，已知∠D＝30°. ‎ ‎⑴判断CD与⊙O的位置关系，请说明理由。‎ ‎⑵若弦CF⊥AB，垂足为E，且CF＝，求图中阴影部分的面积.‎ 答案：（1）CD与⊙O相切………………..1分 理由：连接OC……………2分 ‎∵AC=DC，∴∠A=∠D=30°‎ ‎∵AO=CO，∴∠OCA=∠A=30°………….3分 ‎∠COD=60°，∴∠D+∠COD=90°，∴∠OCD=90°‎ ‎∴OC⊥CD, ∴CD与⊙O相切………………4分 ‎（2）∵CF⊥AB，∴CE=CF=……………..5分 在Rt△OCE中，sin60=, OC=2‎ OE=1 ,-==…………..7分 ‎6．（南京市下关区秦淮区沿江区2011年中考一模）‎ ‎ (10分)如图直角坐标系中，已知A(－4，0)，B(0，3)，点M在线段AB上．‎ ‎ (1)如图1，如果点M是线段AB的中点，且⊙M的半径为2，试判断直线OB与⊙M的位置关系，并说明理由；‎ 图1‎ 图2‎ ‎(2)如图2，⊙M与x轴、y轴都相切，切点分别是点E、F，试求出点M的坐标．‎ 答案：(1)直线OB与⊙M相切． ……………………1分 理由：‎ 设线段OB的中点为D，连结MD．……………………2分 因为点M是线段AB的中点，所以MD∥AO，MD＝2．‎ 所以MD⊥OB，点D在⊙M上．……………………4分 又因为点D在直线OB上，……………………5分 所以直线OB与⊙M相切．‎ ‎(2) 解法一：可求得过点A、B的一次函数关系式是y＝x＋3，………………7分 因为⊙M与x轴、y轴都相切，‎ 所以点M到x轴、y轴的距离都相等．……………………8分 设M(a，－a) (－4＜a＜0) ．‎ 把x＝a，y＝－a代入y＝x＋3，‎ 得－a＝a＋3，得a＝－．……………………9分 所以点M的坐标为(－，)．……………………10分 解法二：连接ME、MF．设ME＝x(x＞0)，则OE＝MF＝x，…………6分 AE＝x，所以AO＝x．………………8分 因为AO＝4，所以，x＝4．‎ 解得x＝．……………………9分 所以点M的坐标为(－，)．……………………10分 ‎7．（南京市浦口区2011年中考一模）（7分）如图，内接于⊙，点在半径的延长线上，．‎ ‎（1）判断直线与⊙的位置关系，并说明理由；‎ A O C B D ‎（2）若⊙的半径长为1，求由弧、线段和所围成的阴影部分面积（结果保留和根号）．‎ 答案：（本题7分）‎ 解：（1）直线与⊙O相切．------------------------------------------ 1分 理由：在⊙O中，．‎ 又，是正三角形，.-------------------2分 又，，‎ ‎．-------------------------------------------------- 3分 又是半径，直线与⊙O相切．----------------------------- 4分 ‎（2）由（1）得是，．‎ ‎，．------------------------------------------ 5分 ‎．-------------------------------------- 6分 又，‎ ‎．---------------------- 7分 ‎8．（南京市六合区2011年中考一模）（8分）如图，△ABC中，AB=4，AC=2，BC=2，以BC为直径的半圆交AB于 点D，以A为圆心，AC为半径的扇形交AB于点E．‎ ‎（1）以BC为直径的圆与AC所在的直线有何位置关系？请说 明理由；‎ ‎（2）求图中阴影部分的面积（结果可保留根号和）．‎ 答案：解：（1）相切．……………………1分 理由：∵22+(2)2=16=42, ∴AC2+BC2=AB2 ． ∴∠ACB=90°．‎ ‎∴以BC为直径的圆与AC所在的直线相切．……………………4分 ‎（2）∵Rt△ABC中，cosA= = ．‎ ‎∴∠A=60°．……………………5分 ‎∴S阴影=S半圆–（S△ABC–S扇形ACE）= π()2–(´2´2–π´22)=–2．……8分 ‎9．（南京市江宁区2011年中考一模）(本题12分) 在正方形网格中以点为圆心，为半径作圆交网格于点（如图（1）），过点作圆的切线交网格于点，以点为圆心，为半径作圆交网格于点 ‎（如图（2））．‎ 图15‎ 问题：‎ ‎（1）求的度数；‎ ‎（2）求证：；‎ ‎（3）可以看作是由经过怎样的变换得到的？并判断的形状（不用说明理由）．‎ ‎（4）如图（3），已知直线，且a∥b，b∥c，在图中用直尺、三角板、圆规画等边三角形，使三个顶点，分别在直线上．要求写出简要的画图过程，不需要说明理由．‎ 答案：（1）连接BC，由网格可知点C在AB的中垂线上，‎ ‎∴AC=BC，…………………………………………………………………………………1分 ‎∵AB=AC，‎ ‎∴AB=BC=AC，即是等边三角形.……………………………………………2分 ‎∴=60°；…………………………………………………………………………3分 ‎（2）∵CD切⊙A于点C，‎ ‎∴‎ ‎.…………………………………………………………………4分 在Rt与Rt中，‎ ‎∵AB=AC,AE=AD.……………………………………………………………………5分 ‎∴ （HL）.……………………………………………………6分 ‎（3）可以看作是由绕点A顺时针旋转60°得到的. …………7分 是等边三角形.………………………………………………………………8分 ‎（4）在直线a上任取一点，记为点A′，作A′M′⊥b，垂足为点M′；作线段A′M′的垂直平分线，此直线记为直线d；以点A′为圆心，A′M′长为半径画圆，与直线d交于点N′；………………………9分 过点N′作N′C′⊥A′N′交直线c于点C′；……………………………………10分 以点A′为圆心，A ′C′ 长为半径画圆，此圆交直线b于点B′； ……………11分 连接A′B′、B′C′，则△A′B′C′为所求等边三角形.………………………12分 ‎10. （南京市建邺区2011年中考一模）（8分）如图，在△ABC中，AB=AC，点O为底边上的中点，以点O为圆心，1为半径的半圆与边AB相切于点D．‎ D B C A O ‎（第9题图）‎ ‎ （1）判断直线AC与⊙O的位置关系，并说明理由；‎ ‎ （2）当∠A＝60°时，求图中阴影部分的面积．‎ 解：（1）直线AC与⊙O相切． 1分 理由是：‎ 连接OD,过点O作OE⊥AC，垂足为点E．‎ ‎∵⊙O与边AB相切于点D，‎ ‎∴OD⊥AB． 2分 ‎∵AB=AC，点O为底边上的中点，‎ ‎∴AO平分∠BAC 3分 又∵OD⊥AB，OE⊥AC ‎∴OD= OE 4分 ‎∴OE是⊙O的半径．‎ 又∵OE⊥AC，∴直线AC与⊙O相切． 5分 ‎（2）∵AO平分∠BAC，且∠BAC=60°， ∴∠OAD=∠OAE=30°，‎ ‎∴∠AOD=∠AOE=60°，‎ 在Rt△OAD中，∵tan∠OAD = ，∴AD==，同理可得AE=‎ ‎∴S四边形ADOE =×OD×AD×2=×1××2= 6分 又∵S扇形形ODE==π 7分 ‎∴S阴影= S四边形ADOE －S扇形形ODE=－π． 8分 ‎11.（南京市鼓楼区2011年中考一模）（8分）如图，△ABC中,∠B＝45°,∠C＝30°,AC＝2，以A为圆心，1为半径画⊙A．‎ ‎（1）判断直线BC与⊙A的位置关系，并说明理由；‎ ‎（2）求图中阴影部分面积（结果保留根号）．‎ C B A ‎。解：（1）直线BC与⊙A相切． ‎ 理由如下：过点A作AD⊥BC，垂足为D，…………………………1分 在Rt△ADC，∠C＝30°，AC＝2，‎ ‎∴AD＝AC＝1．…………………………3分 又∵⊙A半径为1，‎ ‎∴直线BC与⊙A相切．…………………………5分 ‎（2）∵AD⊥BC，∠B＝45°，AD＝1，∠C＝30°，‎ ‎∴BD＝1．CD＝,∴BC＝BD＋CD＝1＋.‎ ‎∴S△ABC＝BC×AD＝×（1＋）×1＝．………………………6分 图中阴影部分的面积等于 S△ABC－S扇形＝－＝－．…………………………8分 ‎12．（南京市高淳县2011年中考一模）(9分)如图，AB为⊙O内垂直于直径的弦，AB、CD相于点H，△AED与△AHD关于直线AD成轴对称． ‎ ‎（1）试说明：AE为⊙O的切线；‎ P A B O C D E H ‎（第11题）‎ ‎（2）延长AE与CD交于点P，已知PA＝2，PD＝1，求⊙O的半径和DE的长．‎ 答案：(9分) （1）连结OA 由△AED与△AHD关于直线AD成轴对称可知∠ADO＝∠ADE ………1分 因为AB⊥CD，所以∠AED＝∠AHD＝90°．‎ 又因为OA＝OD，所以∠OAD＝∠ODA …………………2分 所以∠OAD＝∠ADE，所以OA∥DE ………3分 所以∠OAP＝90°，又因为点A在圆上，所以AE为⊙O的切线． ………4分 C A B O D E H ‎（2）设⊙O的半径为x,在Rt△AOP中，‎ OA2＋AP2＝OP2‎ x2＋22＝(x＋1)2 ………5分 解得x＝1.5‎ P 所以⊙O的半径为1.5 ………7分 因为OA∥DE，所以△PED∽△PAO ‎ ‎ 所以＝，＝，解得DE＝ ………9分 ‎13、（2011名校联合一模）如图直角坐标系中，已知A(－4，0)，B(0，3)，点M在线段AB上．‎ ‎ (1)如图1，如果点M是线段AB的中点，且⊙M的半径为2，试判断直线OB与⊙M的位置关系，并说明理由；‎ 图1‎ 图2‎ ‎(2)如图2，⊙M与x轴、y轴都相切，切点分别是点E、F，试求出点M的坐标．‎ ‎[来源:学.科.网Z.X.X.K]‎ 考查内容：直线与圆的位置关系 答案：‎ ‎(1)直线OB与⊙M相切． ……………………1分 理由：‎ 设线段OB的中点为D，连结MD．……………………2分 因为点M是线段AB的中点，所以MD∥AO，MD＝2．‎ 所以MD⊥OB，点D在⊙M上．……………………4分 又因为点D在直线OB上，……………………5分 所以直线OB与⊙M相切．‎ ‎(2) 解法一：可求得过点A、B的一次函数关系式是y＝x＋3，………………7分 因为⊙M与x轴、y轴都相切，‎ 所以点M到x轴、y轴的距离都相等．……………………8分 设M(a，－a) (－4＜a＜0) ．‎ 把x＝a，y＝－a代入y＝x＋3，‎ 得－a＝a＋3，得a＝－．……………………9分 所以点M的坐标为(－，)．……………………10分 解法二：连接ME、MF．设ME＝x(x＞0)，则OE＝MF＝x，……………………6分 AE＝x，所以AO＝x．………………8分 因为AO＝4，所以，x＝4．‎ 解得x＝．……………………9分 所以点M的坐标为(－，)．……………………10分 ‎14、（2011朝阳区一模） 已知：如图，⊙O的半径OC垂直弦AB 于点H，连接BC，过点A作弦AE∥BC，过点C作CD∥BA交EA延长线于点D，延长CO交AE于点F．‎ ‎ （1）求证：CD为⊙O的切线；‎ ‎ （2）若BC＝5，AB＝8，求OF的长．‎ 考查内容: 直线与圆的位置关系 答案：（1）证明：∵OC⊥AB，CD∥BA，‎ ‎∴∠DCF=∠AHF=90°.[来源:学科网]‎ ‎∴CD为⊙O的切线. ……………… 2分 ‎（2）解：∵OC⊥AB，AB＝8，‎ ‎∴AH=BH==4. ‎ 在Rt△BCH中，∵BH=4，BC=5， ‎ ‎∴CH=3. ……………………………… 3分 ‎∵AE∥BC，∴∠B=∠HAF.‎ ‎∴△HAF≌△HBC. ‎ ‎∴FH=CH=3，CF=6. ………………………………………………………… 4分 连接BO，设BO=x，则OC=x，OH=x-3.‎ 在Rt△BHO中，由，解得. …………………… 5分 ‎∴. .…………………………………………………… 6分 ‎15、(2011海淀一模) 如图，AB为⊙O的直径，AB=4，点C在⊙O上， CF⊥OC，且CF=BF.‎ ‎（1）证明BF是⊙O的切线;‎ ‎（2）设AC与BF的延长线交于点M，若MC=6，求∠MCF的大小.‎ 考查内容: ‎ 答案：证明：连接OF.‎ ‎（1） ∵ CF⊥OC,‎ ‎∴ ∠FCO=90°.‎ ‎∵ OC=OB，‎ ‎∴ ∠BCO=∠CBO.‎ ‎∵ FC=FB，‎ ‎∴ ∠FCB=∠FBC. …………………………..1分 ‎∴ ∠BCO+∠FCB =∠CBO+∠FBC.‎ 即 ∠FBO=∠FCO=90°.‎ ‎∴ OB⊥BF.‎ ‎∵ OB是⊙O的半径,‎ ‎∴ BF是⊙O的切线. …………………………..2分 ‎ ‎ ‎（2） ∵ ∠FBO=∠FCO=90°，‎ ‎∴ ∠MCF+∠ACO =90°，∠M+∠A =90°.‎ ‎∵ OA=OC，‎ ‎∴ ∠ACO=∠A.‎ ‎∴ ∠FCM=∠M. ……………………………………3分 易证△ACB∽△ABM,‎ ‎∴ .‎ ‎∵ AB=4，MC=6，‎ ‎∴ AC=2. ………………………………………..4分 ‎∴ AM=8，BM==.‎ ‎∴cos∠MC F = cosM ==. ‎ ‎∴ ∠MCF=30°. ……………………………………..5分 ‎16、(2011怀柔一模) （本题满分5分）如图，已知AB为⊙O的直径,DC切⊙O于点C,过D点作 DE⊥AB,垂足为E,DE交AC于点F. 求证：△DFC是等腰三角形. ‎ 证明： ‎ 考查内容：‎ 答案：证明：连结OC，∵OA=OC ∴∠OAC=∠OCA……………（1分）‎ ‎∵DC是切线 ‎∴∠DCF=900-∠OCA……………（2分）‎ ‎∵DE⊥AB ‎∴∠DFC=900-∠OAC……………（3分）‎ ‎∵∠OAC=∠OCA，……………（4分）‎ ‎∴∠DFC=∠DCF……………（5分）即△DFC是等腰三角形. ‎ ‎17、(2011黄冈张榜中学模拟) （满分6分）如图，四边形ABCD内接于⊙O，CD∥AB，且AB是⊙O的直径，AE⊥CD交CD延长线于点E.‎ ‎(1)求证：AE是⊙O的切线； ‎ ‎(2)若AE=2，CD=3，求⊙O的直径.‎ 考查内容：‎ 答案：（1）证明：由AE⊥CD，可证∠EDA＋∠EAD＝90°；易证∠EDA＝∠ABC＝∠BAD，所以∠BAD＋∠EAD＝90°，即∠EAB＝90°，故AE为⊙O的切线。‎ ‎（2）作OF⊥CD于F，连结OD，可证OF＝AE＝2，由垂径定理可得，，由勾股定理得，所以直径AB＝5。‎ ‎6、(2011平顶山二模) （10分）如图，Rt△ABC中，＜ACB=90°,AC=4 ,AB=5 ,点P是AC上的动点（P不与A、C重合），设PC=x,点P到AB的距离PQ为y.‎ ‎（1）求y与x的函数表达式，并写出自变量x的取值范围；‎ ‎（2）试讨论以P为圆心、半径长为x的圆与AB所在直线的位置关系，并指出相应的x取值范围.‎ 考查内容: ‎ 答案：解:(1)在Rt△ABC中,由勾股定理可得:BC=. ……1分 由题意可知:∠PQA=∠C=900,∠A=∠A,AP=AC-PC=4-x,‎ ‎∴△APQ∽△ABC ∴ ,即: , ………………3分 变形得y与x的函数表达式为:,‎ 其中自变量x的取值范围为:0＜x＜4. ………………5分 ‎(2)令PC=PQ,即,解得:x=. ………………7分 ‎∴当0＜x＜时,以P为圆心、半径长为x的圆与AB所在直线相离; ………………8分 当x=时, 以P为圆心、半径长为x的圆与AB所在直线相切; ………………9分 当＜x＜4时,以P为圆心、半径长为x的圆与AB所在直线相交. ………………10分 ‎18、（2011年徐汇区诊断卷） （本题满分12分，第（1）题7分，第（2）题5分）‎ 如图，在⊙O中，直径AB与弦CD垂直，垂足为E，连接AC，A F C G O D E B 将△ACE沿AC翻折得到△ACF，直线FC与直线AB相交于点G．‎ ‎（1）证明：直线FC与⊙O相切；‎ ‎（2）若，求证：四边形OCBD是菱形．‎ 考查内容: ‎ 答案：（1）连接． …………………………………………………………1分 A F C G O D E B ‎（第23题）‎ ‎1‎ ‎3‎ ‎2‎ ‎∵， ∴ …………………………………………1分 由翻折得，，．…1分 ‎∴． …………………………………1分 ‎∴OC∥AF．……………………………… ……1分 ‎∴．…………………………1分 ‎∵点C在圆上 ‎∴直线FC与⊙O相切． ………………………1分 ‎（2）解一：在Rt△OCG中，∵，∴， …………1分 ‎∵直径AB垂直弦CD， ∴ ………………………1分 ‎∴ ………………………1分 ‎∵‎ ‎∴． ………………………1分 ‎∴四边形OCBD是菱形． ………………………1分 解二：在Rt△OCG中，∵，∴， ………………1分 ‎∵，∴ ………………………1分 ‎∵AB垂直于弦CD， ∴ ………………………1分 ‎∵直径AB垂直弦CD， ∴ ………………………1分 ‎∴四边形OCBD是平行四边形 ‎∵AB垂直于弦CD，∴四边形OCBD是菱形． …………………………………1分 ‎19. （2011年从化市综合测试）‎ 图8‎ 如图8，△OAB中，OA=OB，，⊙O经过AB的中点E交OA，OB于C，D两点，连接CD.‎ ‎（1）求证：AB是⊙O的切线；‎ ‎（2）求证：CD∥AB；‎ ‎（3）若，求弧的长（结果保留）.‎ 证明：（1）连接OE． ‎ ‎∵OA=OB，E是AB的中点，‎ ‎∴OE⊥AB． ‎ ‎∴AB是⊙O的切线． ‎ ‎（2）在△OAB，△OCD中，‎ ‎∵∠COD=∠AOB，CO=OD，OA=OB，‎ ‎∴∠OCD=∠OAB． ‎ ‎∴CD∥AB． ‎ 解：（3）∵CD∥AB，∠A=30°，OE⊥AB，,设OE交CD于F ‎∴∠OCD=30°，OE⊥CD，CF=，∠COD=120°．‎ OC= =4． ‎ 弧的长= ‎ ‎20. （2011番禺区综合训练）图12‎ 如图12，AB是⊙O的直径，AE平分∠BAF交⊙O于点E，过点E作直线与AF垂直，交AF延长线于点D，交AB延长线于点C. ‎ ‎（1）判断CD是否是⊙O的切线, 并说明理由.‎ ‎ （2）若⊙O的半径为1, 求的长.‎ 答案: 图12‎ 证明：（1）连结OE， ‎ ‎∵OA＝OE，‎ ‎∴∠OAE＝∠OEA， ‎ 又∵∠DAE＝∠OAE，‎ ‎∴∠OEA＝∠DAE， ‎ ‎∴OE∥AD. ‎ ‎. ‎ ‎∵AD⊥CD，‎ ‎, 故.‎ ‎∴OE⊥CD ,∴CD是⊙O的切线. ‎ ‎（2），‎ 又 ，. ‎ 在中, 即, .‎ 在中, 即, . ‎ ‎21. （2011萝岗区综合测试一)如图，已知点E在直角△ABC的斜边AB上，以AE为直径的⊙O与直角边BC相切于点D，∠B = 30°．‎ 求证：（1）AD平分∠BAC，（2）若BD = ，求B E的长．‎ ‎ 答案：证明：‎A C D O E B ‎1‎ ‎2‎ ‎3‎ ‎（1）连接OD ‎ ‎ ∵BC是⊙O的切线 ‎∴OD⊥BC ‎ 又∵AC⊥BC ‎ ‎∴OD∥AC，‎ ‎∴∠2 =∠3；‎ ‎∵OA = OD，‎ ‎∴∠1 =∠3；‎ ‎∴∠1 =∠2；‎ ‎∴AD平分∠BAC，‎ ‎（2）在Rt△ODB中，∠ODB=90°， ∠B=30°， BD=．‎ ‎∵ ‎ ‎∴OD=BD·tanB=×=3‎ ‎∴BO=2OD =6‎ ‎∵OE=OD=3，∴BE=BO-OE=6-3=3‎ A C D O E B ‎1‎ ‎2‎ 第19题图 ‎ . ‎ ‎22（2011年天河区综合练习）在边长为10的正方形ABCD中，以AB为直径作半圆O，如图①，E是半圆上一动点，过点E作EF⊥AB，垂足为F，连结DE.‎ ‎（1）当DE=10时，求证：DE与圆O相切；‎ ‎（2）求DE的最长距离和最短距离；‎ ‎（3）如图②，建立平面直角坐标系，当DE =10时，试求直线DE的解析式.‎ 第24题---①‎ ① 第24题---②‎ 第25题 ‎ ‎ 第25题 ‎24.（本题满分14分）‎ ‎24题第（1）问答案 ‎（1）证明：连结，由题意得，‎ ‎，，为公共边 ‎∴ ‎ ‎24题第（2）问答案 ‎∴‎ ‎（利用勾股定理逆定理相应给分）‎ ‎∴‎ ‎∴与圆相切 ‎（2）当点运动到与点重合的位置时，‎ 为正方形的对角线，所以此时最长，有：‎ 当点运动到线段与半圆的交点处时，最短.‎ 证明如下：‎ 在半圆上任取一个不与点重合的点，连结，.‎ 在中，∵ 即：，‎ ‎∵ ∴‎ ‎∵点是任意一个不与点重合的点，∴此时最短. ‎ ‎∴‎ ‎（3）当点E与点A重合时，DE=DA=10，此时，直线DE的解析式为y=10；‎ ‎-‎ ‎24题第（3）问答案 当点E与点A不重合时，过点E作GH ⊥轴，分别交 ‎，轴于点，，连结.‎ 则四边形是矩形，且为圆的切线 ‎∴=90°‎ ‎∴‎ 又∵‎ ‎∴∽‎ ‎∴‎ 设，则有：，‎ 得：，‎ 解得：， 即：‎ 又直线DE过点D(10,10),设直线解析式为，则有：，‎ 解得：，即：‎ ‎∴当时，直线的解析式为或 以下两种解法涉及高中知识，仅供参考：‎ 另解2:‎ ‎（1）当点E与点A重合时，DE=DA=10，此时，直线DE的解析式为y=10；‎ ‎（2）当点E与点A不重合时，，[来源:学|科|网Z|X|X|K]‎ 设直线且经过点（10，10），代入求得 所以直线DE的解析式为 另解3:‎ 依题意得:点O的坐标为(0,5),设直线DE的解析式为 由点到直线的距离公式得: ,即 ①‎ 直线DE过点D(10,10),得 ②‎ 由①②解得：，解得 所以直线DE的解析式为 ‎23. （2011广州六校一摸）如图，点在的直径的延长线上，点在上，，，‎ ‎（1）求证：是的切线；‎ ‎（2）若的半径为3，求的长．（结果保留）‎ A O B D C 答案.‎ ‎（1）证明：连结， ‎ ‎， ‎ A O B D C ‎1‎ ‎2‎ ‎，， ‎ ‎，．‎ ‎ 是的切线．‎ ‎（2），‎ 的长=． ‎ 答：的长为 ‎5. （2010海珠区调研）如图,是圆的直径,为圆心,、是半圆的弦，且. 延长交圆的切线于点 ‎(1) 判断直线是否为的切线，并说明理由；‎ ‎(2) 如果，，求的长。‎ ‎（3）将线段以直线为对称轴作对称线段,点正好在圆上，如图2，求证：四边形为菱形 ‎ ‎ 答案: 证明：连结OD ∵是圆的直径 ∴∠ADB=90° ‎ ‎∴∠ADO+∠BDO=90° 又∵DO=BO ∴∠BDO=∠PBD ‎ ‎∵ ∴∠BDO=∠PDA ‎ ‎∴∠ADO+∠PDA=90° 即PD⊥OD ‎ ‎∵点D在⊙O上，‎ ‎∴直线为⊙O的切线. ‎ ‎（2）解：∵ BE是⊙O的切线 ∴∠EBA=90°‎ ‎∵ ∴∠P=30° ‎ ‎∵为⊙O的切线 ∴∠PDO=90°‎ 在RT△PDO中，∠P=30° ∴ 解得OD=1 ‎ ‎∴ ‎ ‎∴PA=PO-AO=2-1=1 ‎ ‎（3）（方法一）证明：依题意得：∠ADF=∠PDA ∠PAD=∠DAF ‎∵ ∠ADF=∠ABF ‎∴∠ADF=∠PDA=∠PBD=∠ABF ‎ ‎∵是圆的直径 ∴∠ADB=90° ‎ 设∠PBD=，则∠DAF=∠PAD=，∠DBF=‎ ‎∵四边形AFBD内接于⊙O ∴∠DAF+∠DBF=180°‎ 即 解得 ‎ ‎∴∠ADF=∠PDA=∠PBD=∠ABF=30° ‎ ‎∵ BE、ED是⊙O的切线 ∴DE=BE ∠EBA=90°‎ ‎∴∠DBE=60°∴△BDE是等边三角形。∴BD=DE=BE ‎ 又∵∠FDB=∠ADB—∠ADF =90°-30°=60° ∠DBF==60°‎ ‎∴△BDF是等边三角形。 ∴BD=DF=BF ‎ ‎∴DE=BE=DF=BF ∴四边形为菱形 ‎ ‎（方法二）证明：依题意得：∠ADF=∠PDA ∠APD=∠AFD ‎∵ ∠ADF=∠ABF ∠PAD=∠DAF ‎∴∠ADF=∠AFD=∠BPD=∠ABF ‎ ‎∴ AD=AF BF//PD ‎ ‎∴ DF⊥PB ∵ BE为切线 ∴ BE⊥PB ∴ DF//BE ‎ ‎∴四边形为平行四边形 ‎ ‎∵ PE 、BE为切线 ∴ BE=DE ‎∴四边形为菱形 ‎ ‎24. (2011增城市综合测试)如图，与⊙O相切于点，，⊙O的直径为 4，AB=8‎ 求：（1）的长；‎ ‎（2）的值．‎ O A C B 答案: （1）由已知，OC=2，BC=4。‎ ‎ 在Rt△OBC中，由勾股定理，得 ‎ ‎ ‎ （2）在Rt△OAC中，∵OA=OB=，OC=2，‎ ‎ ∴sinA= ‎ ‎[来源:学|科|网]‎ B组 ‎40.直线与圆的位置关系 一 选择题 ‎1. (2011广东化州市中考模拟)设⊙O的半径为‎4cm，点O到直线L的距离是d,若⊙O与直线无公共点，则（ ）‎ A．d=5 B．05 D．d≤5‎ 答案:‎ ‎2. (2011广东化州市中考模拟) 如图，PA切⊙O于点A，PO=6，，则图中阴影部分的面积为，则∠P=（ ）‎ A. 45° B. 60° C. 30° D. 75°‎ 答案:C 图3‎ ‎3.(2011年白云区初中毕业班综合测试)如图3，Ｐ为⊙Ｏ外一点，ＰＡ切⊙Ｏ于点Ａ，‎ 且ＯＰ＝１０，ＰＡ＝６，则sin∠ＡＰＯ等于（＊）‎ ‎（Ａ）　（Ｂ）　（Ｃ）　（Ｄ）‎ 答案 B ‎4.（2011北京平谷区一模） 如图，是的直径，弦，是弦的中点，‎ ‎．若动点以的速度从点出发沿着方向运动，设运动时间为，连结，当是直角三角形时，‎ ‎（s）的值为 ‎ ‎ A． B．‎1 ‎‎ C．或1 D．或1 或 ‎ 答案 D ‎5.（2011北京石景山一模）已知：⊙O的半径为‎2cm，圆心到直线l的距离为‎1cm，将直线l沿垂直于l的方向平移，使l与⊙O相切，则平移的距离是 （ ） ‎ O B C D A 第6题 A．‎1 cm B．‎2 cm C．‎3cm D．‎1 cm或‎3cm 答案 D ‎6 (2011武汉样卷) 如图，AB是⊙O的直径，AD是⊙O的切线，‎ 点C在⊙O上，BC∥OD，AB=2，OD=3，则BC的长为（ ）‎ ‎ A． B． C． D． 答案 A 二 填空题 ‎1. （2011河南三门峡模拟一）如图（1），PA、PB分别切O于点A、B，点E是O上一点，用∠AEB = ‎60℃‎，则∠P的度数为 .‎ 答案：60‎ ‎2.(广州四中2011年初三第一次模拟测试)如图所示，AB，AC与⊙O相切于点B，C，∠A＝50°，点P是圆上异于B，C的一动点，则∠BPC的度数是______________‎ ‎  ‎ 图13‎ ‎ 答案 65 或115 ‎ ‎ ‎ ‎3.(广州四中2011年初三第一次模拟测试)如图13，两根铁棒直立于桶底水平的木桶中，在桶中加入水后，一根露出水面的长度是它的1/3，另一根露出水面的长度是它的1/5．两根 铁棒长度之和为55 cm， 此时木桶中水的深度是 cm．‎ 答案 20‎ 三 解答题 ‎1.（2011河南三门峡模拟一）（本小题满分10分）‎ 如图，O是△ABC的外接圆，AB = AC，过点A作AP∥BC，交BO的延长线于P.‎ ‎（1）求证：AP是O的切线；‎ ‎（2）若O的半径R = 6，△ACD为等边三角形时，求线段AP的长.‎ 证明：（1）∵‎ 作等腰三角形底边BC上的高AD，‎ ‎ ∴AD过圆心O，.……2分 ‎ 在Rt⊿ACD中∠DAC+∠DCA=90°‎ ‎ ∵‎ ‎ ∴∠PAC=∠DCA ‎ ∴∠DAC+∠PAC =90°‎ ‎∴是⊙的切线.……6分 ‎（2）∵⊿ACD为等边三角形 ‎ ∴∠ABP=30°，‎ ‎∴∠AOP=60°.……8分 在Rt⊿AOP中 ‎.……10分 O D C B A ‎（第2题）‎ ‎2．（2011南京白下区模拟测试一）（8分）如图，在△ABC中，AB＝AC，∠B＝30°，O是BC上一点，以点O为圆心，OB长为半径作圆，恰好经过点A，并与BC交于点D．‎ ‎（1）判断直线CA与⊙O的位置关系，并说明理由；‎ ‎（2）若AB＝2，求图中阴影部分的面积（结果保留π）．‎ 解：（1）直线CA与⊙O相切． …………………………………………1分 O D C B A ‎ 如图，连接OA．‎ ‎ ∵AB＝AC，∠B＝30°，‎ ‎∴∠C＝∠B＝30°，∠DOA＝2∠B＝60°．‎ ‎………………2分 ‎ ∴∠CAO＝90°，即OA⊥CA． ……………3分 ‎∵点A在⊙O上，‎ ‎ ∴直线CA与⊙O相切．‎ ‎…………………………………………………………………4分 ‎ （2）∵AB＝2，AB＝AC，‎ ‎ ∴ AC＝2． ………………………………………………………………5分 ‎∵OA⊥CA，∠C＝30°，‎ ‎∴OA＝AC·tan30°＝2·＝2． ……………………………………6分 ‎∴S扇形OAD＝＝π．……………………………………………………7分 ‎∴图中阴影部分的面积等于S△AOC－S扇形OAD＝2－π． ………………8分 ‎3．（2011北京丰台区统一练习）在Rt中，∠F=90°，点B、C分别在AD、FD上，以AB为直径的半圆O 过点C，联结AC，将△AFC 沿AC翻折得，且点E恰好落在直径AB上.‎ ‎（1）判断：直线FC与半圆O的位置关系是_______________；并证明你的结论.‎ ‎（2）若OB=BD=2,求CE的长．‎ 解：（1）直线FC与⊙O的位置关系是_相切_；………………‎‎1’‎ 证明：联结OC ‎∵OA=OC，∴∠1=∠2，由翻折得，∠1=∠3，∠F=∠AEC=90°‎ ‎∴∠3=∠2 ……………………………………………………‎‎2’‎ ‎∴OC∥AF，∴∠F=∠OCD=90°，∴FC与⊙O相切 …………‎‎3’‎ ‎（2）在Rt△OCD中，cos∠COD=‎ ‎ ∴∠COD=60° …………………………‎‎4’‎ ‎ 在Rt△OCD中，CE=OC·sin∠COD= ………………………‎‎5’‎ ‎4.(2010-2011学年两校联考综合测试)‎ 如图，已知AB是⊙O的直径，PA是⊙O的切线，过点B作 BC∥OP交⊙O于点C，连接AC.‎ ‎（1）求证：△ABC∽△POA ；‎ 答案 ‎（2）若AB=2，PA=，求BC的长（结果保留根号）.‎ 答案 ‎(1) ∵AB是⊙O的直径 ∴ …………………………2分 ‎∵PA是⊙O的切线 ∴ …………………………4分 ‎∵ BC∥OP ∴ ‎ 则 △ABC∽△POA ………………………………………………6分 ‎ (2) ∵AB是⊙O的直径，且AB=2‎ ‎ ∴OA=1 ……………………7分 ‎∵在中，PA=‎ ‎∴ ……………9分 ‎∵由(1)可知△ABC∽△POA ‎ ∴ ……………………………10分 则 ……………………11分[来源:Z_xx_k.Com]‎ ‎∴求得 …………………………12分 ‎5(2011年浙江嵊州新昌中考数学模拟试题)图①是一个小朋友玩“滚铁环”的游戏，将这个游戏抽象为数学问题如图②，已知铁环的半径为‎25cm，设铁环中心为，铁环与地面接触点为，铁环钩与铁环的接触点为，铁环钩与手的接触点是，铁环钩长‎75cm, 表示点距离地面的高度.‎ ‎ (1)当铁环钩与铁环相切时(如图③)，切点离地面的高度为‎5cm，求水平距离 的长；‎ ‎ (2)当点与点同一水平高度时(如图④)，铁环容易向前滚动，现将如图③铁环钩的一端从点提升到与点同一水平高度的点，铁环钩的另一端点从点上升到点，且水平距离保持不变，求的长（精确到‎1cm）.‎ 解:（1）如图四边形，是矩形，‎ ‎ 中， 2分 方法一 ∵是圆的切线，∴‎ ‎∴,‎ 得,又, ∴ ‎ ‎∽△AIB,得 即得 2分 ‎ (cm) 1分 方法二：∵是圆的切线，∴‎ ‎∴,‎ 得,∴‎ 中， 2分 P ‎（cm） 1分 ‎(2)如图3，四边形是矩形，‎ ‎ 1分 中;‎ 中, 2分 ‎,‎ ‎() 2分 ‎6.（2011北京东城一模）已知：AB是⊙O的弦，OD⊥AB于M交⊙O于点D，CB⊥AB交AD的延长线于C．‎ ‎（1）求证：AD＝DC；‎ ‎（2）过D作⊙O的切线交BC于E，若DE＝2，CE=1，‎ 求⊙O的半径．‎ 答案（1）证明：在⊙O中，OD⊥AB，CB⊥AB，‎ ‎∴AM＝MB，OD∥BC. …………………1分 ‎∴AD＝DC. ……………2分 ‎（2）∵DE为⊙O切线， ‎ ‎∴OD⊥DE ……………3分 ‎ ‎∴四边形MBED为矩形.‎ ‎∴DE∥AB. ……………4分 ‎∴MB=DE=2，MD=BE＝EC=1.‎ 连接OB.‎ 在Rt△OBM中，OB2=OM2+BM2. ‎ 解得 OB= . …………………5分 ‎7.（2011北京平谷区一模）如图，在中，，是角平分线，‎ 平分交于点，经过两点的交于 点，交于点，恰为的直径．‎ ‎（1）求证：与相切；‎ ‎（2）当时，求的半径．‎ 解：（1）证明：连结，则．‎ ‎∴ ．‎ O B G E C M A F ‎1‎ ‎2‎ ‎3‎ ‎∵ 平分．‎ ‎∴ ．‎ ‎∴ ．‎ ‎∴ ．‎ ‎∴ ．…………………………..1分 在中，‎ ‎∵ ，是角平分线，‎ ‎∴ ．………………………………………………………………………..….2分 ‎∴ ．‎ ‎∴ ．‎ ‎∴ ．‎ ‎∴ 与相切．………………………………………………………………………3分 ‎（2）解：在中，，是角平分线，‎ ‎∴．‎ ‎∵，‎ ‎∴,‎ 在中，，‎ ‎∴．………………………………………………………………….4分 设的半径为，则．‎ ‎∵，‎ ‎∴．‎ ‎∴ ．‎ ‎∴ ．‎ 解得．∴ 的半径为．………………………………………………………….5分 ‎8.（2011北京怀柔一模）如图，已知AB为⊙O的直径,DC切⊙O于点C,过D点作 DE⊥AB,垂足为E,DE交AC于点F. 求证：△DFC是等腰三角形.‎ 答案 证明：连结OC，∵OA=OC ∴∠OAC=∠OCA……………（1分）‎ ‎∵DC是切线 ‎∴∠DCF=900-∠OCA……………（2分）‎ ‎∵DE⊥AB ‎∴∠DFC=900-∠OAC……………（3分）‎ ‎∵∠OAC=∠OCA，……………（4分）‎ ‎∴∠DFC=∠DCF……………（5分）即△DFC是等腰三角形. ‎ ‎9（2011北京石景山一模）．已知：如图，在矩形中，点在对角线上，以的长为半径的⊙与，分别交于点E、点F，且∠=∠．‎ ‎（1）判断直线与⊙的位置关系，并证明你的结论；‎ ‎（2）若，，求⊙的半径．‎ 答案 解：(1)直线与⊙O相切……………………………………………………1分 证明：联结 在矩形中, ∥‎ ‎∴∠=∠‎ ‎∵‎ ‎∴∠=∠‎ 又∵∠=∠‎ ‎∴∠=∠……………………………………………………………2分 ‎∵矩形,∠‎ ‎∴‎ ‎∴‎ ‎∴………………………………………………………………3分 ‎∴直线与⊙O相切 ‎(2) 联结 方法1：‎ ‎∵四边形是矩形,‎ ‎∴,‎ ‎∵∠=∠‎ ‎∴‎ ‎∴…………………………………………………4分 在中,可求 ‎∴勾股定理求得 在中，‎ 设⊙O的半径为 则 ‎∴= ……………………………………………………………………5分 方法2：∵是⊙O的直径 ‎∴‎ ‎∵四边形是矩形 ‎∴,‎ ‎ ∵∠=∠‎ ‎∴‎ 设，则 ‎∵‎ ‎∴ ……………………………………………………………4分 ‎∵‎ ‎∴‎ ‎∴‎ ‎∴‎ ‎∴为中点．‎ ‎∵为直径，∠‎ ‎∴‎ ‎∴‎ ‎∴⊙O的半径为 ……………………………………………………………5分 ‎10（2011路桥二中一模）如图，四边形ABCD是平行四边形，以AB为直径的⊙O经过点D，E是⊙O上一点，且∠AED＝45º．‎ ‎ （1）试判断CD与⊙O的关系，并说明理由；‎ ‎（2）若⊙O的半径为‎3cm，AE＝‎4 cm．求∠ADE的正弦值．‎ 答案 21.（1） 直线CD与圆O相切； ……………………… 1分 连接OD，则∠AOD=2∠AED=90°，‎ ‎∵四边形ABCD是平行四边形，∴AB//DC，‎ ‎      ∴∠CDO=∠AOD=90°，∴OD⊥CD，∴直线CD与圆O相切；……… 4分 ‎    (2) 连接BE，则∠ADE=∠ABE，∵AB是圆O的直径，‎ ‎      ∴∠AEB=90°，AB=6. ……………………… 2分 ‎      在Rt△ABE中，sin∠ABE=AE/AB = 2/3， ……………………… 2分∴sin∠ADE=sin∠ABE=2/3. ……………………… 1分 ‎11（2011从化综合）‎ 图8‎ 如图8，△OAB中，OA=OB，，⊙O经过AB的中点E交OA，OB于C，D两点，连接CD.‎ ‎（1）求证：AB是⊙O的切线；‎ ‎（2）求证：CD∥AB；‎ ‎（3）若，求弧的长（结果保留）.‎ 答案 证明：（1）连接OE． …………1分 ‎∵OA=OB，E是AB的中点，‎ ‎∴OE⊥AB． …………3分 ‎∴AB是⊙O的切线． …………4分 ‎（2）在△OAB，△OCD中，‎ ‎∵∠COD=∠AOB，CO=OD，OA=OB，‎ ‎∴∠OCD=∠OAB． …………6分 ‎∴CD∥AB． …………8分 解：（3）∵CD∥AB，∠A=30°，OE⊥AB，,设OE交CD于F ‎∴∠OCD=30°，OE⊥CD，CF=，∠COD=120°．‎ OC= =4． …………10分 弧的长= …………12分