中考二次函数复习题9M 112页

一、选择题 1、（2009 年台湾）向上发射一枚炮弹，经 x 秒后的高度为 y 公尺，且时间与高度关系为 y=ax2bx。若此炮 弹在第 7 秒与第 14 秒时的高度相等，则再下列哪一个时间的高度是最高的？ (A) 第 8 秒 (B) 第 10 秒 (C) 第 12 秒 (D) 第 15 秒 。 【关键词】二次函数极值 【答案】B 2、（2009 年泸州）在平面直角坐标系中，将二次函数 22xy  的图象向上平移 2 个单位，所得图象的解析 式为 A． 22 2  xy B． 22 2  xy C． 2)2(2  xy D． 2)2(2  xy 【关键词】二次函数图像的平移。 【答案】B 3、 (2009 年四川省内江市)抛物线 3)2( 2  xy 的顶点坐标是（ ） A．（2，3） B．（－2，3） C．（2，－3） D．（－2，－3） 【关键词】二次函数的顶点坐标. 【答案】A 4、（2009 年长春）如图，动点 P 从点 A 出发，沿线段 AB 运动至点 B 后，立即按原路返回，点 P 在运动 过程中速度大小不变，则以点 A 为圆心，线段 AP 长为半径的圆的面积 S 与点 P 的运动时间 t 之间的函数 图象大致为（ ） 5、（2009 年桂林市、百色市）二次函数 2( 1) 2y x   的最小值是（ ）． A．2 B．1 C．－3 D． 2 3 【关键词】二次函数的极值问题 【答案】A 6、(2009 年上海市)抛物线 22( )y x m n   （ m n， 是常数）的顶点坐标是（ ） A． ( )m n， B． ( )m n ， C． ( )m n， D． ( )m n ， 【关键词】抛物线的顶点 【答案】B 7、(2009 年陕西省)根据下表中的二次函数 cbxaxy  2 的自变量 x 与函数 y 的对应值，可判断二次函数 的图像与 x 轴 【 】 x … －1 0 1 2 … y … －1 4 7 －2 4 7 … A．只有一个交点 B．有两个交点，且它们分别在 y 轴两侧 C．有两个交点，且它们均在 y 轴同侧 D．无交点 【关键词】二次函数的图象 【答案】B 8、（2009 威海）二次函数 23 6 5y x x    的图象的顶点坐标是（ ） O S t O S t O S t O S t A P B A． B． C． D． （第 8 题） A． ( 18) ， B． (18)， C． ( 1 2) ， D． (1 4)， 【关键词】抛物线顶点 【答案】A 9、（2009 湖北省荆门市）函数 y=ax＋1 与 y=ax2＋bx＋1（a≠0）的图象可能是（ ） A． B． C． D． 解析：本题考查函数图象与性质，当 0a  时，直线从左向右是上升的，抛物线开口向上，D 是错的，函数 y=ax＋1 与 y=ax2＋bx＋1（a≠0）的图象必过（0，1），所以 C 是正确的，故选 C． 【关键词】函数图象与性质 【答案】C 10、（2009 年贵州黔东南州）抛物线的图象如图所示，根据图象可知，抛物线的解析式可能．．是（ ） A、y=x2-x-2 B、y= 12 1 2 1 2  x C、y= 12 1 2 1 2  xx D、y= 22  xx 【关键词】二次函数 2y ax bx c   （a≠0）与 a，b，c 的关系 【答案】D 11、（2009 年齐齐哈尔市）已知二次函数 2 ( 0)y ax bx c a    的图象如图所示，则下列结论： 0ac ① ； ② 方程 2 0ax bx c   的两根之和大于 0； y③ 随 x 的增大而增大；④ 0a b c   ，其中正确的个数（） A．4 个 B．3 个 C．2 个 D．1 个 【关键词】二次函数 2y ax bx c   （a≠0）与 a，b，c 的关系、二次函数的图象 【答案】C x y O 1 12、（2009 年深圳市）二次函数 cbxaxy  2 的图象如图 2 所示，若点 A（1，y1）、B（2，y2）是它图象 上的两点，则 y1 与 y2 的大小关系是（ ） A． 21 yy  B． 21 yy  C． 21 yy  D．不能确定 【关键词】二次函数 2y ax bx c   （a≠0）与 a，b，c 的关系 【答案】C 12、（2009 桂林百色）二次函数 2( 1) 2y x   的最小值是（ ）． A．2 B．1 C．－3 D． 2 3 【关键词】二次函数、最值 【答案】A 13、（2009 丽水市）已知二次函数 y＝ax2＋bx＋c(a≠0)的图象如图所示，给出以下结论： ①a＞0. ②该函数的图象关于直线 1x  对称. ③当 1 3x x  或 时，函数 y 的值都等于 0. 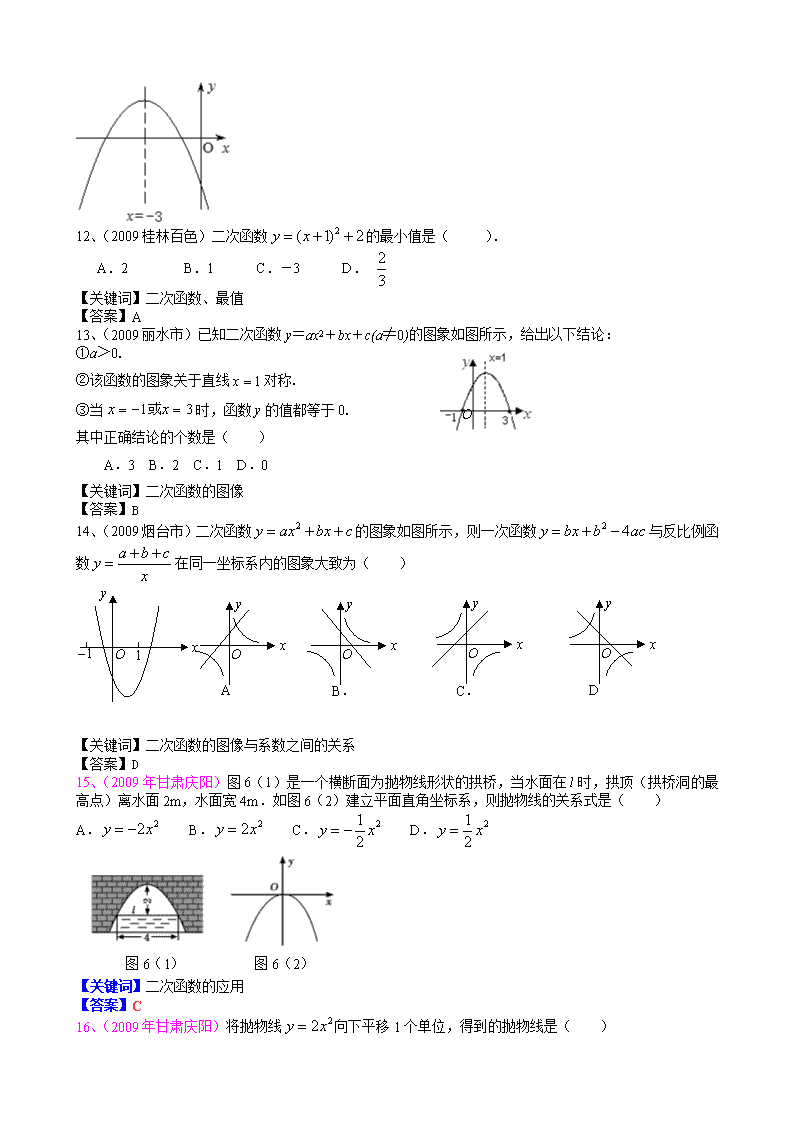其中正确结论的个数是（ ） A．3 B．2 C．1 D．0 【关键词】二次函数的图像 【答案】B 14、（2009 烟台市）二次函数 2y ax bx c   的图象如图所示，则一次函数 2 4y bx b ac   与反比例函 数 a b cy x   在同一坐标系内的图象大致为（ ） 1 1O x y 【关键词】二次函数的图像与系数之间的关系 【答案】D 15、（2009 年甘肃庆阳）图 6（1）是一个横断面为抛物线形状的拱桥，当水面在 l 时，拱顶（拱桥洞的最 高点）离水面 2m，水面宽 4m．如图 6（2）建立平面直角坐标系，则抛物线的关系式是（ ） A． 22y x  B． 22y x C． 21 2y x  D． 21 2y x 图 6（1） 图 6（2） 【关键词】二次函数的应用 【答案】C 16、（2009 年甘肃庆阳）将抛物线 22y x 向下平移 1 个单位，得到的抛物线是（ ） y xO y xO B． C． y xO A． y xO D． O A． 22( 1)y x  B． 22( 1)y x  C． 22 1y x  D． 22 1y x  【关键词】二次函数和抛物线有关概念 【答案】D 17、（2009 年广西南宁）已知二次函数 2y ax bx c   （ 0a  ）的图象如图 4 所示，有下列四个结论： 20 0 4 0b c b ac   ① ② ③ ④ 0a b c   ，其中正确的个数有（ ） A．1 个 B．2 个 C．3 个 D．4 个 1 图 4 O x y 3 【关键词】二次函数 2y ax bx c   （a≠0）与 a，b，c 的关系 【答案】C 18、(2009 年鄂州)已知=次函数 y＝ax 2 +bx+c 的图象如图．则下列 5 个代数式：ac，a+b+c，4a－2b+c， 2a+b，2a－b 中，其值大于 0 的个数为（ ） A．2 B 3 C、4 D、5 【关键词】二次函数 2y ax bx c   （a≠0）与 a，b，c 的关系 【答案】A 19、（2009 年孝感）将函数 2y x x  的图象向右平移 a ( 0)a  个单位，得到函数 2 3 2y x x   的图象， 则 a 的值为 A．1 B．2 C．3 D．4 【关键词】二次函数图象的平移 【答案】B 20、（2009 泰安）抛物线 182 2  xxy 的顶点坐标为 （A）（-2，7） （B）（-2，-25） （C）（2，7） （D）（2，-9） 【关键词】抛物线的顶点 【答案】C。 21、（2009 年烟台市）二次函数 2y ax bx c   的图象如图所示，则一次函数 2 4y bx b ac   与反比例 函数 a b cy x   在同一坐标系内的图象大致为（ ） 【关键词】一次函数、反比例函数与二次函数之间的有关系 【答案】D. 1 1O x y y xO y xO B． C． y xO A． y xO D． 22、（2009 年嘉兴市）已知 0a ，在同一直角坐标系中，函数 axy  与 2axy  的图象有可能是（ ▲ ） 【关键词】一次函数、二次函数之间的关系 【答案】C 23、（2009 年新疆）如图，直角坐标系中，两条抛物线有相同的对称轴，下列关系不正确．．．的是（ ） A． h m B． k n C． k n D． 0 0h k ， 【关键词】二次函数的对称轴 【答案】B 24、（2009 年天津市）在平面直角坐标系中，先将抛物线 2 2y x x   关于 x 轴作轴对称变换，再将所得 的抛物线关于 y 轴作轴对称变换，那么经两次变换后所得的新抛物线的解析式为（ ） A． 2 2y x x    B． 2 2y x x    C． 2 2y x x    D． 2 2y x x   【关键词】二次函数的解析式 【答案】C 25、（2009 年南宁市）已知二次函数 2y ax bx c   （ 0a  ）的图象如图所示，有下列四个结论： 20 0 4 0b c b ac   ① ② ③ ④ 0a b c   ，其中正确的个数有（ ） A．1 个 B．2 个 C．3 个 D．4 个 【关键词】二次函数 2y ax bx c   （a≠0）与 a，b，c 的关系 【答案】C 26、（2009 年衢州）二次函数 2( 1) 2y x   的图象上最低点的坐标是 A．(-1，-2) B．(1，-2) C．(-1，2) D．(1，2) 【关键词】抛物线顶点和对称轴 【答案】B 27、（2009 年舟山）二次函数 2( 1) 2y x   的图象上最低点的坐标是 A．(-1，-2) B．(1，-2) C．(-1，2) D．(1，2) 【关键词】抛物线顶点和对称轴 【答案】B O y x1 1 A． x y O1 1 B． x y O1 1 C． x y O1 1 D． 28、（2009 年广州市）二次函数 2)1( 2  xy 的最小值是（ ） A.2 （B）1 （C）-1 （D）-2 【关键词】二次函数 【答案】A 29、（2009 年济宁市）小强从如图所示的二次函数 2y ax bx c   的图象中，观察得出了下面五条信息： （1） 0a  ；（2） 1c  ；（3） 0b  ；（4） 0a b c   ； （5） 0a b c   . 你认为其中正确信息 的个数有 A．2 个 B．3 个 C．4 个 D．5 个 1 21 1 O 1 x y （第 12 题） 【关键词】二次函数 【答案】C 30、（2009 年广西钦州）将抛物线 y＝2x2 向上平移 3 个单位得到的抛物线的解析式是（ ） A．y＝2x2＋3 B．y＝2x2－3 C．y＝2（x＋3）2 D．y＝2（x－3）2 【关键词】二次函数的图像 【答案】A 31、(2009 宁夏)二次函数 2 ( 0)y ax bx c a    的图象如图所示，对称轴是直线 1x  ，则下列四个结论 错误．．的是（ ）D A． 0c  B． 2 0a b  C． 2 4 0b ac  D． 0a b c   【关键词】二次函数的图象 【答案】D 1 1 1 O x y （8 题图） 32、(2009 年南充)抛物线 ( 1)( 3)( 0)y a x x a    的对称轴是直线（ ） A． 1x  B． 1x   C． 3x   D． 3x  【关键词】抛物线的对称轴 【答案】A 33、(2009 年湖州)已知图中的每个小方格都是边长为 1 的小正方形，每个小正方形的顶点称为格点，请你 在图中任意画一条抛物线，问所画的抛物线最多能经过 81 个格点中的多少个？（ ） A．6 B．7 C．8 D．9 【关键词】抛物线 【答案】C 34、（2009 年兰州）在同一直角坐标系中，函数 y mx m  和函数 2 2 2y mx x    （ m 是常数，且 0m  ） 的图象可能．．是 【关键词】一次函数与 二次函数的图像和性 质 【答案】D 35、（2009 年兰州）把抛物线 2y x  向左平移 1 个单位，然后向上平移 3 个单位，则平移后抛物线的解析 式为 A． 2( 1) 3y x    B． 2( 1) 3y x    C． 2( 1) 3y x    D． 2( 1) 3y x    【关键词】二次函数的图像和性质、平移 【答案】D 36、（2009 年兰州）二次函数 cbxaxy  2 的图象如图 6 所示， 则 下 列 关 系式不正确的是 A． a ＜0 B. abc ＞0 C. cba  ＞0 D. acb 42  ＞0 【关键词】二次函数的图像和性质与系数 a,b,c 之间的关系 【答案】C 37、（2009 年遂宁）把二次函数 34 1 2  xxy 用配方法化成   khxay  2 的形式 A.   224 1 2  xy B.   424 1 2  xy C.   424 1 2  xy D. 32 1 2 1 2       xy 【关键词】二次函数的图像的解析式 【答案】D 39、（2009 年广州市）二次函数 2)1( 2  xy 的最小值是（ ） A.2 （B）1 （C）-1 （D）-2 【关键词】二次函数 【答案】A 40、（2009 年济宁市）小强从如图所示的二次函数 2y ax bx c   的图象中，观察得出了下面五条信息： （1） 0a  ；（2） 1c  ；（3） 0b  ；（4） 0a b c   ； （5） 0a b c   . 你认为其中正确信息 的个数有 A．2 个 B．3 个 C．4 个 D．5 个 1 21 1 O 1 x y （第 12 题） 【关键词】二次函数 【答案】C 41、（2009 年台湾）向上发射一枚炮弹，经 x 秒后的高度为 y 公尺，且时间与高度关系为 y=ax2bx。若此 炮弹在第 7 秒与第 14 秒时的高度相等，则再下列哪一个时间的高度是最高的？ (A) 第 8 秒 (B) 第 10 秒 (C) 第 12 秒 (D) 第 15 秒 。 【关键词】二次函数极值 【答案】B 42、(2009 年河北)某车的刹车距离 y（m）与开始刹车时的速度 x（m/s）之间满足二次函数 21 20y x （x ＞0），若该车某次的刹车距离为 5 m，则开始刹车时的速度为（ ） A．40 m/s B．20 m/s C．10 m/s D．5 m/s 【关键词】二次函数的运算 【答案】C 43、（2009 年湖北荆州）抛物线 23( 1) 2y x   的对称轴是（ ） A． 1x  B． 1x   C． 2x  D． 2x   【关键词】二次函数对称轴 【答案】 44、（2009 年新疆乌鲁木齐市）要得到二次函数 2 2 2y x x    的图象，需将 2y x  的图象（ ）． A．向左平移 2 个单位，再向下平移 2 个单位 B．向右平移 2 个单位，再向上平移 2 个单位 C．向左平移 1 个单位，再向上平移 1 个单位 D．向右平移 1 个单位，再向下平移 1 个单位 【关键词】二次函数和抛物线有关概念 【答案】D 45、（2009 年黄石市）已知二次函数 2y ax bx c   的图象如图所示，有以下结论：① 0a b c   ；② 1a b c   ；③ 0abc  ；④ 4 2 0a b c   ；⑤ 1c a  其中所有正确结论的序号是（ ） A．①② B． ①③④ C．①②③⑤ D．①②③④⑤ 1 1 1 O x y 【关键词】二次函数 2y ax bx c   （a≠0）与 a，b，c 的关系 【答案】C 46、（2009 黑龙江大兴安岭）二次函数 )0(2  acbxaxy 的图象如图，下列判断错误的是 （ ） A． 0a B． 0b C． 0c D． 042  acb 【关键词】二次函数 2y ax bx c   （a≠0）与 a，b，c 的关系 【答案】B 47、（ 2009 年 枣 庄 市 ） 二次函数 cbxaxy  2 的图象如图所示，则下列关系式中错误．．的是（ ） A．a＜0 B．c＞0 C． acb 42  ＞0 D． cba  ＞0 【关键词】二次函数 2y ax bx c   （a≠0）与 a，b，c 的关系 【答案】D 二、填空题 1、（2009 年北京市）若把代数式 2 2 3x x  化为 2x m k  的形式，其中 ,m k 为常数，则 m k = . 【关键词】配方法 【答案】-3 2、（2009 年安徽）已知二次函数的图象经过原点及点（ 1 2  ， 1 4  ），且图象与 x 轴的另一交点到原 点的距离为 1，则该二次函数的解析式为 【关键词】二次函数和抛物线有关概念，待定系数法 【答案】 2y x x  ， 21 1 3 3y x   3、已知二次函数的图象经过原点及点（ 1 2  ， 1 4  ），且图象与 x 轴的另一交点到原点的距离为 1，则该二 次函数的解析式为 ． 【关键词】待定系数法 【答案】 2y x x  ， 21 1 3 3y x   4、（2009 年郴州市）抛物线 23( 1) 5y x=- - + 的顶点坐标为__________． 【关键词】二次函数的顶点坐标 【答案】 (15)， 5、(2009 年上海市)12．将抛物线 2 2y x  向上平移一个单位后，得以新的抛物线，那么新的抛物线的 表达式是 ． 【关键词】抛物线的平移 【答案】 12  xy 6、（2009 年内蒙古包头）已知二次函数 2y ax bx c   的图象与 x 轴交于点 ( 2 0) ， 、 1( 0)x， ，且 11 2x  ， 第 11 题图 y xO 1－1 与 y 轴的正半轴的交点在 (0 2)， 的下方．下列结论：① 4 2 0a b c   ；② 0a b  ；③ 2 0a c  ；④ 2 1 0a b   ．其中正确结论的个数是 个． 【答案】4 【解析】本题考查二次函数图象的画法、识别理解，方程根与系数的关系筀等知识和数形结合能力。根据 题意画大致图象如图所示，由 2y ax bx c   与 X 轴的交点坐标为(-2,0)得    22 2 0a b c       ， 即 4 2 0a b c   所以①正确； 由图象开口向下知 0a  ，由 2y ax bx c   与 X 轴的另一个交点坐标为  1,0x 且 11 2x  ，则该抛物 线的对称轴为   12 1 2 2 2 xbx a       由 a<0 得 b>a,所以结论②正确， 由一元二次方程根与系数的关系知 1 2. 2cx x a    ，结合 a<0 得 2 0a c  ，所以③结论正确， 由 4 2 0a b c   得 2 2 ca b   ，而 00,所以结论 ④正确。 点拨： 4 2 0a b c   是否成立，也就是判断当 2x   时， 2y ax bx c   的函数值是否为 0； 判断 2y ax bx c   中 a 符号利用抛物线的开口方向来判断，开口向上 a>0,开口向下 a<0;判断 a、b 的小 关系时，可利用对称轴 2 bx a   的值的情况来判断；判断 a、c 的关系时，可利用由一元二次方程根与系 数的关系 1 2. cx x a  的值的范围来判断；2a-b+1 的值情况可用 4 2 0a b c   来判断。 7、（2009 襄樊市）抛物线 2y x bx c    的图象如图 6 所示，则此抛物线的解析式为 ． y xO 3 x=1 图 6 解析：本题考查二次函数的有关知识，由图象知该抛物线的对称轴是 1x  ，且过点（3，0），所以 12 9 3 0 b b c        ，解得 2 3 b c    ，所以抛物线的解析式为 2 2 3y x x    ， 故填 2 2 3y x x    。 【关键词】函数解析式 【答案】 2 2 3y x x    8、（2009 湖北省荆门市）函数 ( 2)(3 )y x x   取得最大值时， x  ______． 解析：本题考查二次函数的最值问题，可以用配方法或二次函数顶点坐标公式求出当 x 为何值时二次函数 取得最大值，下面用配方法， 2 2 5 49( 2)(3 ) 5 6 2 4y x x x x x              ，所以当 5 2x  时，函数 ( 2)(3 )y x x   取得最大值，故 填 5 2 【关键词】二次函数最值 【答案】 5 2 9、（2009 年淄博市） 请写出符合以下三个条件的一个函数的解析式 ． ①过点 (31)，； ②当 0x  时，y 随 x 的增大而减小； ③当自变量的值为 2 时，函数值小于 2． 答案：如 21 3 1 523 6 2y x y y xx       ， ， 10、（2009 年贵州省黔东南州）二次函数 322  xxy 的图象关于原点 O（0, 0）对称的图象的解析式 是_________________。 【关键词】待定系数法 【答案】 322  xxy 11、（2009 年齐齐哈尔市）当 x  _____________时，二次函数 2 2 2y x x   有最小值． 【关键词】二次函数的极值问题 【答案】 1 12、（2009 年娄底）如图 7，⊙O 的半径为 2，C1 是函数 y= 1 2 x2 的图象，C2 是函数 y=- 1 2 x2 的图象，则阴影 部分的面积是 . 【关键词】对称性、圆的面积 【答案】2π 13、（2009 年甘肃庆阳）图 12 为二次函数 2y ax bx c   的图象，给出下列说法： ① 0ab  ；②方程 2 0ax bx c   的根为 1 21 3x x  ， ；③ 0a b c   ；④当 1x  时，y 随 x 值的 增大而增大；⑤当 0y  时， 1 3x   ． 其中，正确的说法有 ．（请写出所有正确说法的序号） 【关键词】二次函数 2y ax bx c   （a≠0）与 a，b，c 的关系 【答案】①②④ 14、(2009 年鄂州)把抛物线 y＝ax 2 +bx+c 的图象先向右平移 3 个单位，再向下平移 2 个单位，所得的图 象的解析式是 y＝x 2 －3x+5，则 a+b+c=__________ 【关键词】二次函数图象的平移 【答案】11 15、（2009 白银市）抛物线 2y x bx c    的部分图象如图 8 所示，请写出与其关系式、图象相关的 2 个 正确结论： ， ．（对称轴方程，图象与 x 正半轴、y 轴交点坐标 例外） 【关键词】二次函数 2y ax bx c   （a≠0）与 a，b，c 的关系、二次函数与一元二次方程根之间的内在 联系、二次函数与一元二次不等式的关系 【答案】答案不唯一．如：①c=3；②b+c=1；③c-3b=9；④b=-2；⑤抛物线的顶点为（-1，4），或二次函 数的最大值为 4；⑥方程-x2+bx+c=0 的两个根为-3，1；⑦y>0 时，-31； ⑧当 x>-1 时，y 随 x 的增大而减小；或当 x<-1 时，y 随 x 的增大而增大．等等 16、(2009 年甘肃定西)抛物线 2y x bx c    的部分图象如图 8 所示，请写出与其关系式、图象相关的 2 个正确结论： ， ．（对称轴方程，图象与 x 正半轴、y 轴交点坐 标例外） 【关键词】二次函数的图像 【答案】答案不唯一. 17、（2009 年包头）将一条长为 20cm 的铁丝剪成两段，并以每一段铁丝的长度为周长各做成一个正方形， 则这两个正方形面积之和的最小值 是 cm2． 【关键词】面积、最小值 答案： 25 2 或12.5 18、（2009 年包头）已知二次函数 2y ax bx c   的图象与 x 轴交于点 ( 2 0) ， 、 1( 0)x， ，且 11 2x  ，与 y 轴的正半轴的交点在 (0 2)， 的下方．下列结论：① 4 2 0a b c   ；② 0a b  ；③ 2 0a c  ；④ 2 1 0a b   ．其中正确结论的个数是 个． 【关键词】二次函数 答案：4 19、（2009 年莆田）出售某种文具盒，若每个获利 x 元，一天可售出 6 x 个，则当 x  元时， 一天出售该种文具盒的总利润 y 最大． 【关键词】二次函数、最大值 答案：3 20、(2009 年本溪)如图所示，抛物线 2y ax bx c   （ 0a  ）与 x 轴的两个交点分别为 ( 1 0)A  ， 和 (2 0)B ， ， 当 0y  时， x 的取值范围是 ． 【关键词】二次函数 【答案】 1x   或 2x  21．(2009 年湖州)已知抛物线 2y ax bx c   （ a ＞0）的对称轴为直线 1x  ，且经过点   21 2y y 1， ， ， 试比较 1y 和 2y 的大小： 1y _ 2y （填“>”，“<”或“=”） 【关键词】二次函数的性质 【答案】＞ 22、（2009 年兰州）二次函数 22 3y x 的图象如图 12 所示，点 0A 位 于 坐 标 原 点， 点 1A ， 2A ， 3A ，…， 2008A 在 y 轴的正半轴上，点 1B ， 2B ， 3B ，…， 2008B 在二次函数 22 3y x 位于第一象限的图象上， 若△ 0 1 1A B A ,△ 1 2 2A B A ，△ 2 3 3A B A ，…，△ 2007 2008 2008A B A 都为等边三角形，则△ 2007 2008 2008A B A 的边长＝ . 【关键词】二次函数的图像和性质与三角形面积 【答案】2008 23、（2009 年北京市）若把代数式 2 2 3x x  化为 2x m k  的 形式，其中 ,m k 为常数，则 m k = . 【关键词】配方法 【答案】-3 24．(2009 年咸宁市)已知 A 、B 是抛物线 2 4 3y x x   上位置不同的两点，且关于抛物线的对称轴对称， 则点 A 、 B 的坐标可能是_____________．（写出一对即可） 【关键词】二次函数的对称轴 【答案】(1,0),(3,0) 25、（2009 年安徽）已知二次函数的图象经过原点及点（ 1 2  ， 1 4  ），且图象与 x 轴的另一交点到原 点的距离为 1，则该二次函数的解析式为 ． 【关键词】二次函数解析式 【答案】 2y x x  ， 21 1 3 3y x   26、（2009 年黄石市）若抛物线 2 3y ax bx   与 2 3 2y x x    的两交点关于原点对称，则 a b、 分别 为 ． 【关键词】待定系数法；二元一次方程组的解法 【答案】 3,2 3 27、（2009 黑龙江大兴安岭）当 x 时，二次函数 222  xxy 有最小值． 【关键词】抛物线顶点和对称轴 【答案】-1 三、解答题 1、（2009 年株洲市）如图 1， Rt ABC 中， 90A   ， 3tan 4B  ，点 P 在线段 AB 上运动，点 Q 、 R 分别在线段 BC 、 AC 上，且使得四边形 APQR 是矩形．设 AP 的长为 x ，矩形 APQR 的面积为 y ，已 O 知 y 是 x 的函数，其图象是过点（12，36）的抛物线的一部分（如图 2 所示）． （1）求 AB 的长； （2）当 AP 为何值时，矩形 APQR 的面积最大，并求出最大值． 为了解决这个问题，孔明和研究性学习小组的同学作了如下讨论： 张明：图 2 中的抛物线过点（12，36）在图 1 中表示什么呢？ 李明：因为抛物线上的点 ( , )x y 是表示图 1 中 AP 的长与矩形 APQR 面积的对应关系，那么，（12，36） 表示当 12AP  时， AP 的长与矩形 APQR 面积的对应关系. 赵明：对，我知道纵坐标 36 是什么意思了！ 孔明：哦，这样就可以算出 AB ，这个问题就可以解决了. 请根据上述对话，帮他们解答这个问题. 图 1 【关键词】二次函数最值 【答案】（1）当 12AP  时， 36AP PQ  ∴ 3PQ  ， 又在 Rt BPQ 中， 3tan 4B  ，∴ 3 4 PQ PB  ∴ 4PB  ∴ 16AB  ， （ 2 ） 解 法 一 ： 若 AP x ， 则 16PB x  ， 3 (16 )4PQ x  ， ∴ 3 (16 )4y x x  ， 整 理 得 23 ( 8) 484y x    ，∴ 当 8x  时， 48y最大值＝ . 解法二：由 16AB  ，结合图象可知抛物线经过点（0，0）、（16，0）、（12，36），可设抛物线解析式为 ( 16)y ax x  ，将（12，36）代入求得 3 4a   ，∴ 3 ( 16)4y x x   ，整理得 23 ( 8) 484y x    ， ∴ 当 8x  时， 48y最大值＝ . 解法三：由 16AB  ，结合图象可知抛物线经过点（0，0）、（16，0），知抛物线对称轴为 8x  ，∴抛物 线顶点的横坐标为 8.∴当 8AP  时，矩形 APQR 的面积最大，此时， 8PB  ，∴ 38 64PQ    ，∴最 大面积为 48. 2、（2009 年株洲市）已知 ABC 为直角三角形， 90ACB   ， AC BC ,点 A 、C 在 x 轴上，点 B 坐 标为（3 ， m ）（ 0m  ），线段 AB 与 y 轴相交于点 D ，以 P （1，0）为顶点的抛物线过点 B 、 D ． （1）求点 A 的坐标（用 m 表示）； （2）求抛物线的解析式； （3）设点Q 为抛物线上点 P 至点 B 之间的一动点，连结 PQ 并延长交 BC 于点 E ，连结 BQ 并延长交 AC R Q P C B A 于点 F ，试证明： ( )FC AC EC 为定值． 【关键词】二次函数的综合题 【答案】（1）由 (3, )B m 可知 3OC  ， BC m ，又△ABC 为等腰直角三角形，∴ AC BC m  ， 3OA m  ，所以点 A 的坐标是（ 3 ,0m ）. （2）∵ 45ODA OAD     ∴ 3OD OA m   ，则点 D 的坐标是（ 0, 3m  ）. 又抛物线顶点为 (1,0)P ，且过点 B 、 D ，所以可设抛物线的解析式为： 2( 1)y a x  ，得： 2 2 (3 1) (0 1) 3 a m a m       解得 1 4 a m    ∴抛物线的解析式为 2 2 1y x x   ， （3）过点Q 作 QM AC 于点 M ，过点 Q 作 QN BC 于点 N ，设点 Q 的坐标是 2( , 2 1)x x x  ，则 2( 1)QM CN x   ， 3MC QN x   . ∵ //QM CE ∴ PQM ∽ PEC ∴ QM PM EC PC  即 2( 1) 1 2 x x EC   ，得 2( 1)EC x  ∵ //QN FC ∴ BQN ∽ BFC ∴ QN BN FC BC  即 23 4 ( 1) 4 x x FC    ，得 4 1FC x   又∵ 4AC  ∴ 4 4 4( ) [4 2( 1)] (2 2) 2( 1) 81 1 1FC AC EC x x xx x x             即 ( )FC AC EC 为定值 8. 3、（2009 年重庆市江津区）某商场在销售旺季临近时 ，某品牌的童装销售价格呈上升趋势，假如这种童 装开始时的售价为每件 20 元，并且每周（7 天）涨价 2 元，从第 6 周开始，保持每件 30 元的稳定价格销 售，直到 11 周结束，该童装不再销售。 （1）请建立销售价格 y（元）与周次 x 之间的函数关系； （ 2 ） 若 该 品 牌 童 装 于 进 货 当 周 售 完 ， 且 这 种 童 装 每 件 进 价 z （ 元 ） 与 周 次 x 之 间 的 关 系 为 12)8(8 1 2  xz ， 1≤ x ≤11，且 x 为整数，那么该品牌童装在第几周售出后，每件获得利润最大？ 并求最大利润为多少？ 【关键词】二次函数极值 【答案】【答案】（1） 20 2( 1) 2 18 30 x xy       (1 6)( 11)( ) x x x x     为整数) (6 为整数 （2）设利润为 w 2 2 2 2 1 120 2( 1) ( 8) 12 14(1 6)8 8 1 130 ( 8) 12 ( 8) 18(6 11)8 8 ( y z x x x x xw y z x x x x                            为整数 为整数) 21 148w x  当 5x  时， 117 (8w 最大 元) 21 ( 8) 188w x   当 11x  时， 1 19 18 1 188 8w     最大 119 ( )8  元 综上知：在第 11 周进货并售出后，所获利润最大且为每件 119 8 元. 4、（2009 年重庆市江津区）如图，抛物线 cbxxy  2 与 x 轴交与 A(1,0),B(- 3，0)两点， （1）求该抛物线的解析式； （2）设（1）中的抛物线交 y 轴与 C 点，在该抛物线的对称轴上是否存在点 Q，使得△QAC 的周长最小？ 若存在，求出 Q 点的坐标；若不存在，请说明理由. （3）在（1）中的抛物线上的第二象限上是否存在一点 P，使△PBC 的面积最大？，若存在，求出点 P 的 坐标及△PBC 的面积最大值.若没有，请说明理由. 【关键词】与二次函数有关的面积问题 【答案】解：（1）将 A（1，0）B（-3，0）代入 2y x bx c    中得 1 0 9 3 0 b c b c         ，∴ 2 3 b c     ∴抛物线解析式为： 2 2 3y x x    （2）存在 理由如下：由题意知 A、B 两点关于抛物线的对称轴 1x   对称，∴直线 BC 与 1x   的交点即为 Q 点， 此时△AQC 周长最小，∵ 2 2 3y x x    ，∴C 的坐标为：（0，3），直线 BC 解析式为 3y x  Q 点坐标即为 1 3 x y x      的解，∴ 1 2 x y     ，∴Q（-1，2） 第 26 题图 AB C 5、（2009 年滨州）某商品的进价为每件 40 元．当售价为每件 60 元时，每星期可卖出 300 件，现需降价处 理，且经市场调查：每降价 1 元，每星期可多卖出 20 件．在确保盈利的前提下，解答下列问题： （1）若设每件降价 x 元、每星期售出商品的利润为 y 元，请写出 y 与 x 的函数关系式，并求出自变量 x 的 取值范围； （2）当降价多少元时，每星期的利润最大？最大利润是多少？ （3）请画出上述函数的大致图象． 【关键词】二次函数的实际应用. 【答案】（1）y=(60-x-40)(300+20x)=(20-x) (300+20x)=- 600010020 2  xx ,0≤x≤20； （2）y=-20 6135)5.2( 2 x ,∴当 x==2.5 元,每星期的利润最大，最大利润是 6135 元；（3）图像略. 6、（2009 年滨州） 如图①，某产品标志的截面图形由一个等腰梯形和抛物线的一部分组成，在等腰梯形 ABCD 中， AB DC∥ ， 20cm 30cm 45AB DC ADC   ， ， °．对于抛物线部分，其顶点为CD 的 中点 O ，且过 A B、 两点，开口终端的连线 MN 平行且等于 DC ． （1）如图①所示，在以点 O 为原点，直线 OC 为 x 轴的坐标系内，点C 的坐标为 (15 0)， ， 试求 A B、 两点的坐标； （2）求标志的高度（即标志的最高点到梯形下底所在直线的距离）； （3）现根据实际情况，需在标志截面图形的梯形部分的外围均匀镀上一层厚度为 3cm 的保护膜，如图②， 请在图中补充完整镀膜部分的示意图，并求出镀膜的外围周长． 【关键词】二次函数与等腰梯形. 【答案】（1）A（-10，5），B（10，5）；(2) 7、 (2009 年四川省内江市)如图所示，已知点 A（－1，0），B（3，0），C（0，t），且 t＞0，tan∠BAC=3， 抛物线经过 A、B、C 三点，点 P（2，m）是抛物线与直线 )1(:  xkyl 的一个交点。 （1）求抛物线的解析式； （2）对于动点 Q（1，n），求 PQ+QB 的最小值； （3）若动点 M 在直线l 上方的抛物线上运动， 求△AMP 的边 AP 上的高 h 的最大值。 【关键词】二次函数，三角函数. 【答案】解：（1）由 A（-1，0）知 AO=1，由 tan∠BAC=3， 得 CO=3AO=3， ∴t=3 设抛物线的解析式为 y=a(x+1)(x-3),将点 C（0，3）坐标代入得 a=-1 ∴所求解析式为 y=-x2+2x+3 （2）m=-22+2×2+3=3, P(2,3) 动点 Q（1，n)在直线 x=1 上运动，点 B（3，0）关于直线 x=1 的对称点为 A（-1，0） ∴PQ+QB=PQ+QA∴PQ+QB 的最小值为 PA= 22 3)]1(2[  = 23 （3）将点 P（2，3）的坐标代入 y=k(x+1)得 k=1 ∴直线 l 的解析式为 y=x+1 ∴AP 在 l 上. 设 M（x,-x2+2x+3)，过 M 作 y 轴的平行线交 AP 于 D，则 D（x,x+1), MD=(-x2+2x+3)-(x+1)=-x2+x+2 S△AMP=S△AMD+S△PMD=12(-x2+x+2)(x+1)+ 2 1 (-x2+x+2)(2-x)= 2 3 (-x2+x+2) ∴h= AP S AMP2 = 23 3 (-x2+x+2) = 2 2 (-x2+x+2) = 2 2 [-(x- 2 1 )2+ 4 9 ] N B CD A M y x （第 4 题图①） ） O A B CD （第 4 题图②） ）） 20cm 30cm45° ∴当 x= 2 1 时，h 的最大值为 8 29 8、（2009 仙桃）如图，已知抛物线 y＝x2＋bx＋c 经过矩形 ABCD 的两个顶点 A、B，AB 平行于 x 轴，对角 线 BD 与抛物线交于点 P，点 A 的坐标为(0，2)，AB＝4． (1)求抛物线的解析式； (2)若 S△APO＝ 2 3 ，求矩形 ABCD 的面积． 【关键词】二次函数，矩形. 【答案】解：（1）∵A（0，2），AB=4，∴B（4，2） ∵抛物线 2y x bx c   过 A、B 两点 ∴ 2, 16 4 2 c b c      ，解得 4, 2 b c     ∴抛物线的解析式为 2 4 2.y x x   （2）过 P 点作 PE⊥ y 轴于点 E，∵ 3 2APOS  ， 1 3 2 2OA PE  ∵OA=2，∴ 3 2PE  .∵点 P 在抛物线 2 4 2y x x   上，∴当 3 2x  时， 7 4y   .∴P 点坐标为. 3 7( , )2 4  设直线 BD 的解析式为 y kx b  ∵直线 BD 过 P、B 两点， ∴ 4 2, 3 7 2 4 k b k b      解得 3 ,2 4 k b      ∴直线 BD 的解析式为 3 42y x  . 当 0x  时， 4y   ，∴D（0，－4），∴AD=2+4=6.∴ 4 6 24.ABCDS   矩形 （3）答：存在 理由如下：设 P 点 2( , 2 3)x x x   ( 3 0)x   ，∵ BPC BOCBPCOS S S  四边形 = 9 2BPCOS 四边形 若 BPCOS四边形 有最大值，则 BPCS 就最大，过 P 点作 PE⊥ x 轴于 E，∴ Rt BPEBPCO PEOCS S S 四边形 直角梯形 1 1 ( )2 2BE PE OE PE OC    2 21 1( 3)( 2 3) ( )( 2 3 3)2 2x x x x x x           23 3 9 27( )2 2 2 8x     ，当 3 2x   时， BPCOS四边形 最大= 9 27 2 8  ∴ BPCS 最大= 9 27 9 27 2 8 2 8    ，当 3 2x   时， 2 152 3 4x x    ，∴点 P 坐标为 3 15( , )2 4  . 9、（2009 年长春）如图，直线 3 64y x   分别与 x 轴、y 轴交于 A B、 两点， 直线 5 4y x 与 AB 交于点C ，与过点 A 且平行于 y 轴的直线交于点 D ．点 E 从点 A 出发，以每秒 1 个单位的速度沿 x 轴向左运动．过点 E 作 x 轴的垂线， 分别交直线 AB OD、 于 P Q、 两点，以 PQ 为边向右作正方形 PQMN ，设 正方形 PQMN 与 ACD△ 重叠部分（阴影部分）的面积为 S （平方单位）．点 E 的运动时间为 t （秒）． （1）求点C 的坐标．（1 分） （2）当 0 5t  时，求 S 与t 之间的函数关系式．（4 分） （3）求（2）中 S 的最大值．（2 分） （4）当 0t  时，直接写出点 94 2      ， 在正方形 PQMN 内部时t 的取值范围．（3 分） 【参考公式：二次函数 2y ax bx c   图象的顶点坐标为 24 2 4 b ac b a a     ， ．】 【关键词】平面内点的坐标的意义，二元一次方程组的应用，不等式（组）的简单应用二次函数与一元二 次方程根之间的内在联系 【答案】 解：（1）由题意，得         . 4 5 ,6 4 3 xy xy 解得      .4 15 ,3 y x ∴C（3, 4 15 ）. （2）根据题意，得 AE=t，OE=8-t. ∴点 Q 的纵坐标为 4 5 (8-t)，点 P 的纵坐标为 4 3 t， ∴PQ= 4 5 (8-t)- 4 3 t=10-2t. 当 MN 在 AD 上时，10-2t=t，∴t= 3 10 . 当 0 9 100 ，∴S 的最大值为 2 25 . （4）46. 10、（2009 年郴州市） 如图 11，已知正比例函数和反比例函数的图像都经过点 M（－2， 1- ），且 P（ 1- ， －2）为双曲线上的一点，Q 为坐标平面上一动点，PA 垂直于 x 轴，QB 垂直于 y 轴，垂足分别是 A、B． （1）写出正比例函数和反比例函数的关系式； （2）当点 Q 在直线 MO 上运动时，直线 MO 上是否存在这样的点 Q，使得△OBQ 与△OAP 面积相 等？如果存在，请求出点的坐标，如果不存在，请说明理由； （3）如图 12，当点 Q 在第一象限中的双曲线上运动时，作以 OP、OQ 为邻边的平行四边形 OPCQ， 求平行四边形 OPCQ 周长的最小值． 【关键词】二次函数的极值问题 【答案】（1）设正比例函数解析式为 y kx ，将点 M（ 2 ， 1 ）坐标代入得 1 2k = ，所以正比例函数解 析式为 1 2y x= 2 分 同样可得，反比例函数解析式为 2y x= （2）当点 Q 在直线 DO 上运动时， 设点 Q 的坐标为 1( )2Q m m， ， 于是 21 1 1 1 2 2 2 4OBQS OB BQ m m m△ = = ， 而 1 ( 1) ( 2) 12OAPS△ = - ´ - = ， 所以有， 21 14 m = ，解得 2m   所以点 Q 的坐标为 1(2 1)Q ， 和 2 ( 2 1)Q ，- - （3）因为四边形 OPCQ 是平行四边形，所以 OP＝CQ，OQ＝PC， 而点 P（ 1 ， 2 ）是定点，所以 OP 的长也是定长，所以要求平行四边形 OPCQ 周长的最小值就只需 图 11 图 12 求 OQ 的最小值 因为点 Q 在第一象限中双曲线上，所以可设点 Q 的坐标为 2( )Q n n ， ， 由勾股定理可得 2 2 2 2 4 2( ) 4OQ n nn n= + = - + ， 所以当 22( ) 0n n- = 即 2 0n n- = 时， 2OQ 有最小值 4， 又因为 OQ 为正值，所以 OQ 与 2OQ 同时取得最小值， 所以 OQ 有最小值 2． 由勾股定理得 OP＝ 5 ，所以平行四边形 OPCQ 周长的最小值是 2( ) 2( 5 2) 2 5 4OP OQ+ = + = + ． 10、（2009 年 常 德 市 ）已知二次函数过点 A （0， 2 ），B（ 1 ，0），C（ 5 9 4 8 ， ）． （1）求此二次函数的解析式； （2）判断点 M（1， 1 2 ）是否在直线 AC 上？ （3）过点 M（1， 1 2 ）作一条直线 l 与二次函数的图象交于 E、F 两点（不同于 A，B，C 三点），请自 已给出 E 点的坐标，并证明△BEF 是直角三角形． 【关键词】二次函数 【答案】（1）设二次函数的解析式为 cbxaxy  2 （ 0a  ）， 把 A （0， 2 ），B（ 1 ，0），C（ 5 9 4 8 ， ）代入得 2 0 9 25 5 8 16 4 c a b c a b c              解得 a=2 ， b=0 ， c=－2， ∴ 22 2y x  （2）设直线 AC 的解析式为 ( 0)y kx b k   ， 把 A （0，－2），C（ 5 9 4 8 ， ）代入得 2 9 5 8 4 b k b     ， 解得 5 22k b  ， ，∴ 5 22y x  图 8 当 x=1 时， 5 11 22 2y     ∴M（1， 1 2 ）在直线 AC 上 （3）设 E 点坐标为（ 1 3 2 2  ， ），则直线 EM 的解析式为 4 5 3 6y x  由 2 4 5 3 6 2 2 y x y x       化简得 2 4 72 03 6x x   ，即 1 7( )(2 ) 02 3x x   ， ∴F 点的坐标为（ 7 13 6 18 ， ）． 过 E 点作 EH⊥x 轴于 H，则 H 的坐标为（ 1 02  ，）． ∴ 3 1 2 2EH BH ， ∴ 2 2 23 1 10( ) ( )2 2 4BE    ， 类似地可得 2 2 213 13 1690 845( ) ( )18 6 324 162BF     ， 2 2 240 10 2500 1250( ) ( )18 6 324 162EF     ， ∴ 2 2 210 845 1250 4 162 162BE BF EF     ，∴△BEF 是直角三角形． 11、(2009 年陕西省) 如图，在平面直角坐标系中，OB⊥OA，且 OB＝2OA，点 A 的坐标是(－1，2)． （1）求点 B 的坐标； （2）求过点 A、O、B 的抛物线的表达式； （3）连接 AB，在（2）中的抛物线上求出点 P，使得 S△ABP＝S△ABO． 【关键词】用相似求线段 平面内点的坐标的意义 三点法确定抛物线 存在性探究题 【答案】解：（1）过点 A 作 AF⊥x 轴，垂足为点 F，过点 B 作 BE⊥x 轴，垂足为点 E， 则 AF＝2，OF＝1． ∵OA⊥OB， ∴∠AOF+∠BOE＝90°． 又 ∵∠BOE+∠OBE＝90°， ∴∠AOF＝∠OBE． ∴Rt△AFO∽Rt△OEB． ∴ 2 OA OB AF OE OF BE ． ∴BE＝2，OE＝4． ∴B(4，2)． （2）设过点 A(－1，2)，B(4，2)，O(0，0)的抛物线为 y=ax2+bx+c． 图 8 ∴       .0 ,2416 ,2 c cba cba 解之，得            .0 ,2 3 ,2 1 c b a ∴所求抛物线的表达式为 xxy 2 3 2 1 2  ． （3）由题意，知 AB∥x 轴． 设抛物线上符合条件的点 P 到 AB 的距离为 d， 则 S△ABP＝ AFABdAB  2 1 2 1 ． ∴d＝2． ∴点 P 的纵坐标只能是 0 或 4． 令 y＝0，得 02 3 2 1 2  xx ，解之，得 x＝0，或 x＝3． ∴符合条件的点 P1(0，0)，P2(3，0)． 令 y＝4，得 42 3 2 1 2  xx ，解之，得 2 413 x ． ∴符合条件的点 P3( 2 413  ，4)，P4( 2 413  ，4)． ∴综上，符合题意的点有四个： P1(0，0)，P2(3，0)，P3( 2 413  ，4)，P4( 2 413  ，4)． （评卷时，无 P1(0，0)不扣分） 12、(2009 年黄冈市)新星电子科技公司积极应对 2008 年世界金融危机，及时调整投资方向，瞄准光伏产 业，建成了太阳能光伏电池生产线．由于新产品开发初期成本高，且市场占有率不高等因素的影响，产品 投产上市一年来，公司经历了由初期的亏损到后来逐步盈利的过程（公司对经营的盈亏情况每月最后一天 结算 1 次）．公司累积获得的利润 y（万元）与销售时间第 x（月）之间的函数关系式（即前 x 个月的利润 总和 y 与 x 之间的关系）对应的点都在如图所示的图象上．该图象从左至右，依次是线段 OA、曲线 AB 和 曲 线 BC ， 其 中 曲 线 AB 为 抛 物 线 的 一 部 分 ， 点 A 为 该 抛 物 线 的 顶 点 ， 曲 线 BC 为 另 一 抛 物 线 25 205 1230y x x    的一部分，且点 A，B，C 的横坐标分别为 4，10，12 （1）求该公司累积获得的利润 y（万元）与时间第 x（月）之间的函数关系式； （2）直接写出第 x 个月所获得 S（万元）与时间 x（月）之间的函数关系式（不需要写出计算过程）； （3）前 12 个月中，第几个月该公司所获得的利润最多？最多利润是多少万元？ 【关键词】待定系数法 函数的极值问题 【答案】（1）当 40  x 时，线段 OA 的函数关系式为 xy 10 ; 当 104  x 时， 由于曲线 AB 所在抛物线的顶点为 A（4，－40），设其解析式为   404 2  xay 在 25 205 1230y x x    中，令 x=10，得 320y ；∴B（10，320） ∵B（10，320）在该抛物线上 ∴   40410320 2  a 解得 10a ∴当 104  x 时，   40410 2  xy = 1208010 2  xx 综上可知，        12302055 1208010 10 2 2 xx xx x y (2) 当 40  x 时, 10S  当 105  x 时, 9020  xS 当 1211  x 时, 21010  xS (3) 10 月份该公司所获得的利润最多,最多利润是 110 万元. 13、(2009 武汉)某商品的进价为每件 40 元，售价为每件 50 元，每个月可卖出 210 件；如果每件商品的售 价每上涨 1 元，则每个月少卖 10 件（每件售价不能高于 65 元）．设每件商品的售价上涨 x 元（ x 为正整 数），每个月的销售利润为 y 元． （1）求 y 与 x 的函数关系式并直接写出自变量 x 的取值范围； （2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？ （3）每件商品的售价定为多少元时，每个月的利润恰为 2200 元？根据以上结论，请你直接写出售价 在什么范围时，每个月的利润不低于 2200 元？ 【关键词】二次函数的应用 二次函数的极值问题 【答案】解：（1） 2(210 10 )(50 40) 10 110 2100y x x x x        （ 0 15x ≤ 且 x 为整数）； （2） 210( 5.5) 2402.5y x    ． 10 0a    ，当 5.5x  时， y 有最大值 2402.5． 0 15x ≤ ，且 x 为整数， 当 5x  时，50 55x  ， 2400y  （元），当 6x  时， 50 56x  ， 2400y  （元） 当售价定为每件 55 或 56 元，每个月的利润最大，最大的月利润是 2400 元． （3）当 2200y  时， 210 110 2100 2200x x    ，解得： 1 21 10x x ， ． 当 1x  时，50 51x  ，当 10x  时， 50 60x  ． 当售价定为每件 51 或 60 元，每个月的利润为 2200 元． 当售价不低于 51 或 60 元，每个月的利润为 2200 元． 当售价不低于 51 元且不高于 60 元且为整数时，每个月的利润不低于 2200 元（或当售价分别为 51， 52，53，54，55，56，57，58，59，60 元时，每个月的利润不低于 2200 元）． 14、(2009 武汉)如图，抛物线 2 4y ax bx a   经过 ( 1 0)A  ， 、 (0 4)C ， 两点，与 x 轴交于另一点 B ． （1）求抛物线的解析式； （2）已知点 ( 1)D m m ， 在第一象限的抛物线上，求点 D 关于直线 BC 对称的点的坐标； （3）在（2）的条件下，连接 BD ，点 P 为抛物线上一点，且 45DBP  °，求点 P 的坐标． )4,3,2,1( x ， )109,8,7,6,5( ，x  ， )12,1110( ，x  . y xO A B C 【关键词】待定系数法 求点的坐标 【答案】解：（1）抛物线 2 4y ax bx a   经过 ( 1 0)A  ， ， (0 4)C ， 两点， 4 0 4 4. a b a a     ， 解得 1 3. a b     ， 抛物线的解析式为 2 3 4y x x    ． （2）点 ( 1)D m m ， 在抛物线上， 21 3 4m m m      ， 即 2 2 3 0m m   ， 1m   或 3m  ． 点 D 在第一象限，点 D 的坐标为 (3 4)， ． y xO A B C D E 由（1）知 45OA OB CBA  ， °． 设点 D 关于直线 BC 的对称点为点 E ． (0 4)C ， ， CD AB ∥ ，且 3CD  ， 45ECB DCB    °， E 点在 y 轴上，且 3CE CD  ． 1OE  ， (01)E ， ． 即点 D 关于直线 BC 对称的点的坐标为（0，1）． （3）方法一：作 PF AB⊥ 于 F ， DE BC⊥ 于 E ． y xO A B C D EP F 由（1）有： 4 45OB OC OBC   ， °， 45DBP CBD PBA     °， ． (0 4) (3 4)C D ，， ， ， CD OB ∥ 且 3CD  ． 45DCE CBO    °， 3 2 2DE CE   ． 4OB OC  ， 4 2BC  ， 5 2 2BE BC CE    ， 3tan tan 5 DEPBF CBD BE       ． 设 3PF t ，则 5BF t ， 5 4OF t   ， ( 5 4 3 )P t t   ， ． P 点在抛物线上，  23 ( 5 4) 3( 5 4) 4t t t        ， 0t  （舍去）或 22 25t  ， 2 66 5 25P     ， ． 方法二：过点 D 作 BD 的垂线交直线 PB 于点Q ，过点 D 作 DH x⊥ 轴于 H ．过Q 点作QG DH⊥ 于G ． y xO A B C D P Q G H 45PBD QD DB    °， ． QDG BDH   90 °， 又 90DQG QDG    °， DQG BDH   ． QDG DBH△ ≌△ ， 4QG DH   ， 1DG BH  ． 由（2）知 (3 4)D ， ， ( 13)Q  ， ． (4 0)B ， ，直线 BP 的解析式为 3 12 5 5y x   ． 解方程组 2 3 4 3 12 5 5 y x x y x         ， ， 得 1 1 4 0 x y    ， ； 2 2 2 5 66 .25 x y      ， 点 P 的坐标为 2 66 5 25     ， ． 15、(2009 年安顺)如图，已知抛物线与 x 交于 A(－1，0)、E(3，0)两点，与 y 轴交于点 B(0，3)。 （1） 求抛物线的解析式； （2） 设抛物线顶点为 D，求四边形 AEDB 的面积； （3） △AOB 与△DBE 是否相似？如果相似，请给以证明；如果不相似，请说明理由。 【关键词】待定系数法，相似三角形判定和性质 【答案】（1）∵抛物线与 y 轴交于点（0，3）， ∴设抛物线解析式为 )0(32  abxaxy 根据题意，得      0339 03 ba ba ，解得      2 1 b a ∴抛物线的解析式为 322  xxy (5′) (2)(5′)由顶点坐标公式得顶点坐标为（1，4） 设对称轴与 x 轴的交点为 F ∴四边形 ABDE 的面积= ABO DFEBOFDS S S  梯形 = 1 1 1( )2 2 2AO BO BO DF OF EF DF      = 1 1 11 3 (3 4) 1 2 42 2 2         =9 （3）似 如图，BD= 2 2 2 21 1 2BG DG    ；∴BE= 2 2 2 23 3 3 2BO OE    DE= 2 2 2 22 4 2 5DF EF    ∴ 2 2 20BD BE  , 2 20DE  即： 2 2 2BD BE DE  ,所以 BDE 是直角三角形 ∴ 90AOB DBE     ,且 2 2 AO BO BD BE   , ∴ AOB ∽ DBE 16、（2009 重庆綦江）如图，已知抛物线 ( 1)2 3 3( 0)y a x a    经过点 ( 2 )A  ，0 ，抛物线的顶点为 D ， 过O 作射线OM AD∥ ．过顶点 D 平行于 x 轴的直线交射线OM 于点C ，B 在 x 轴正半轴上，连结 BC ． （1）求该抛物线的解析式； （2）若动点 P 从点O 出发，以每秒 1 个长度单位的速度沿射线OM 运动，设点 P 运动的时间为 ( )t s ．问 当t 为何值时，四边形 DAOP 分别为平行四边形？直角梯形？等腰梯形？ （3）若OC OB ，动点 P 和动点Q 分别从点O 和点 B 同时出发，分别以每秒 1 个长度单位和 2 个长度 单位的速度沿OC 和 BO 运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动的时间 为t ( )s ，连接 PQ ，当t 为何值时，四边形 BCPQ 的面积最小？并求出最小值及此时 PQ 的长． 【关键词】抛物线 【答案】（1）抛物线 2( 1) 3 3( 0)y a x a    经过点 ( 2 0)A  ， ， 30 9 3 3 3a a      二次函数的解析式为： 23 2 3 8 3 3 3 3y x x    （2） D 为抛物线的顶点 (13 3)D ， 过 D 作 DN OB 于 N ，则 3 3DN  ， x y M CD P QO A B 2 23 3 (3 3) 6 60AN AD DAO      ， ° OM AD ∥ ① 当 AD OP 时，四边形 DAOP 是平行四边形 6 6(s)OP t    ② 当 DP OM 时，四边形 DAOP 是直角梯形 过O 作OH AD 于 H ， 2AO  ，则 1AH  （如果没求出 60DAO  °可由 Rt RtOHA DNA△ ∽ △ 求 1AH  ） 5 5(s)OP DH t    ③ 当 PD OA 时，四边形 DAOP 是等腰梯形 2 6 2 4 4(s)OP AD AH t        综上所述：当 6t  、5、4 时，对应四边形分别是平行四边形、直角梯形、等腰梯形． （3）由（2）及已知， 60COB OC OB OCB  °， ，△ 是等边三角形 则 6 2 6 2 (0 3)OB OC AD OP t BQ t OQ t t         ， ， ， 过 P 作 PE OQ 于 E ，则 3 2PE t 1 1 36 3 3 (6 2 )2 2 2BCPQS t t        = 23 3 63 32 2 8t     当 3 2t  时， BCPQS 的面积最小值为 63 38 此时 3 3 3 9 3 33 32 4 4 4 4OQ OP OE QE PE      ， = ， 2 2 2 2 3 3 9 3 3 4 4 2PQ PE QE                 17、（2009 威海）如图，在直角坐标系中，点 A,B,C 的坐标分别为（-1，0），（3，0）。（0，3），过 A,B,C 三点的抛物线的对称轴为直线l ，D 为对称轴l 上一动点． （1） 求抛物线的解析式； （2） 求当 AD+CD 最小时点 D 的坐标； （3） 以点 A 为圆心，以 AD 为半径作⊙A． ①证明：当 AD+CD 最小时，直线 BD 与⊙A 相切． ②写出直线 BD 与⊙A 相切时，D 点的另一个坐标：___________． 【关键词】待定系数法，直线与圆的位置关系 【答案】（1）设抛物线的解析式为 ( 1)( 3)y a x x   ． 将 (0 3)， 代入上式，得3 (0 1)(0 3)a   ． 解，得 1a   ． 抛物线的解析式为 ( 1)( 3)y x x    ． 即 2 2 3y x x    ． （2）连接 BC ，交直线l 于点 D ． 点 B 与点 A 关于直线 l 对称， AD BD  ． AD CD BD CD BC     ． 由“两点之间，线段最短”的原理可知： 此时 AD CD 最小，点 D 的位置即为所求． 设直线 BC 的解析式为 y kx b  ， x y M C D P QO A BNE H OA B C ly x OA B C ly x D E 由直线 BC 过点 (3 0)， ， (0 3)， ，得 0 3 3 . k b b     ， 解这个方程组，得 1 3. k b     ， 直线 BC 的解析式为 3y x   ． 由（1）知：对称轴l 为 2 12 ( 1)x     ，即 1x  ． 将 1x  代入 3y x   ，得 1 3 2y     ． 点 D 的坐标为（1，2）． 说明：用相似三角形或三角函数求点 D 的坐标也可，答案正确给 2 分． （3）①连接 AD ．设直线l 与 x 轴的交点记为点 E ． 由（1）知：当 AD CD 最小时，点 D 的坐标为（1，2）． 2DE AE BE    ． 45DAB DBA    °． 90ADB  °． AD BD ⊥ ． BD 与 A⊙ 相切． ② (1 2)， ． 18、（2009 年内蒙古包头）已知二次函数 2y ax bx c   （ 0a  ）的图象经过点 (1 0)A ， ， (2 0)B ， ， (0 2)C ， ，直线 x m （ 2m  ）与 x 轴交于点 D ． （1）求二次函数的解析式； （2）在直线 x m （ 2m  ）上有一点 E （点 E 在第四象限），使得 E D B、 、 为顶点的三角形与以 A O C、 、 为顶点的三角形相似，求 E 点坐标（用含 m 的代数式表示）； （3）在（2）成立的条件下，抛物线上是否存在一点 F ，使得四边形 ABEF 为平行四边形？若存在，请 求出 m 的值及四边形 ABEF 的面积；若不存在，请说明理由． y xO 【解析】本题考查二次函数关系式求法、坐标系中有关线段的长度与点的坐标之间的关系，探究三角形相 似的条件和判定四边形为平行四边形的条件，涉及到一元二次方程的解法等综合性较强，稍有疏忽就容 易失分。 【答案】(1)根据题意，得 0 4 2 0 2 a b c a b c c           ，解得 1 3 2 a b c        ∴ 2 3 2y x x    。 (2)当ΔEDB∽ΔAOC 时，得 AO CO ED BD  或 AO CO BD ED  。 ∵AO=1，CO=2，BD=m-2，当 AO CO ED BD  时，得 1 2 2ED m   ， ∴ 2 2 mED  。 ∵点 E 在第四象限， ∴ 1 2, 2 mE m      ，当 AO CO BD ED  时，得 1 2 2m ED  ，∴ 2 4ED m  ，∵点 E 在 第四象限， ∴  1 ,4 2E m m 。 (3)假设抛物线上存在一点这 P，使得四边形 ABEF 为平行四边形，则 EF=AB=1，点 F 的横坐标为 m-1,当 点 1E 的坐标为 2, 2 mm      时，点 1F 的坐标为 21, 2 mm     ， ∵点 1F 在抛物线的图象上， ∴    22 1 3 1 22 m m m       ， ∴ 22 11 14 0m m   ， ∴  2 7 2 0m m   ∴ 7 , 22m m  (舍去) ∴ 1 5 3,2 4F     ， ∴ 3 31 4 4ABEFS    。 当点 2E 的坐标为  ,4 2m m 时，点 2F 的坐标为 1,4 2m m  ， ∵点 F2 在抛物线的图象 上， ∴    24 2 1 3 1 2,m m m       ∴ 2 7 10 0,m m   ∴  2 5 0m m   ∴ 2m  (舍去)， 5m  ∴  1 4, 6 ,F  ∴ 1 6 6ABEFS   平行四边形 点拨：（2）中讨论ΔEDB 与ΔAOC 相似的条件时，题目中未用相似符号连接应按不同的对应关系分 情况讨论，否则易漏解。在由线段的长度求 E 点坐标时要注意点的坐标的符号。 （3）中在求是否存在点 E 问题，应先假设存在，列得关系式如果有解，并且符合题意就存在；如果无解 或解得的结果不符合题意，就不存在。 19、（2009 山西省太原市）已知，二次函数的表达式为 24 8y x x  ．写出这个函数图象的对称轴和顶点 坐标，并求图象与 x 轴的交点的坐标． 【关键词】二次函数最值、与坐标轴交点坐标 【答案】 解：在 24 8y x x  中， 4 8 0a b c  ， ， ．∴ 2 28 4 4 4 0 81 42 2 4 4 4 b ac b a a             ， ．4 ∴这个函数图象的对称轴是 1x   ，顶点坐标是： 1 4 ， ． 评分说明：直接写出正确结果也得 2 分．令 y ＝０，则 24 8 0x x  ．解得 1 20 2x x  ， ．∴函数图象与 x 轴的交点的坐标为    0 0 2 0， ， ， ． 20、（2009 湖北省荆门市） 一开口向上的抛物线与 x 轴交于 A（ 2m  ，0），B（m＋2，0）两点，记抛物 线顶点为 C，且 AC⊥BC． （1）若 m 为常数，求抛物线的解析式； （2）若 m 为小于 0 的常数，那么（1）中的抛物线经过怎么样的平移可以使顶点在坐标原点？ （3）设抛物线交 y 轴正半轴于 D 点，问是否存在实数 m，使得△BCD 为等腰三角形？若存在，求出 m 的值；若不存在，请说明理由． O BA C D x y 第 25 题图 解：（1）设抛物线的解析式为：y＝a（x－m＋2）（x－m－2）＝a（x－m）2－4a．∵AC⊥BC，由抛物线的 对称性可知：△ACB 为等腰直角三角形，又 AB＝4，∴C（m， 2 ）代入得 a＝ 1 2 ．∴解析式为：y＝ 1 2 （x －m）2 2 ．（亦可求 C 点，设顶点式） （2）∵m 为小于零的常数，∴只需将抛物线向右平移－m 个单位，再向上平移 2 个单位，可以使抛物 线 y＝ 1 2 （x－m）2 2 顶点在坐标原点． （3）由（1）得 D（0， 1 2 m2 2 ），设存在实数 m，使得△BOD 为等腰三角形．∵△BOD 为直角三角形， ∴只能 OD＝OB．∴ 1 2 m2－2＝|m＋2|，当 m＋2＞0 时，解得 m＝4 或 m＝ 2 （舍）．当 m＋2＜0 时，解 得 m＝0（舍）或 m＝ 2 （舍）；当 m＋2＝0 时，即 m＝ 2 时，B、O、D 三点重合（不合题意，舍），综 上所述：存在实数 m＝4，使得△BOD 为等腰三角形． 20、（2009 年淄博市）如图，在平面直角坐标系中，正方形 OABC 的边长是 2．O 为坐标原点，点 A 在 x 的正半轴上，点 C 在 y 的正半轴上．一条抛物线经过 A 点，顶点 D 是 OC 的中点． （1）求抛物线的表达式； （2）正方形 OABC 的对角线 OB 与抛物线交于 E 点，线段 FG 过点 E 与 x 轴垂直，分别交 x 轴和线段 BC 于 F，G 点，试比较线段 OE 与 EG 的长度； （3）点 H 是抛物线上在正方形内部的任意一点，线段 IJ 过点 H 与 x 轴垂直，分别交 x 轴和线段 BC 于 I、J 点，点 K 在 y 轴的正半轴上，且 OK=OH，请证明△OHI≌△JKC． 解：（1）由题意，设抛物线的解析式为： 2y ax b  ． 将点 D 的坐标（0，1），点 A 的坐标（2，0）代入，得 a = 1 4  ，b=1． 所求抛物线的解析式为 21 14y x   ． （2）由于点 E 在正方形的对角线 OB 上，又在抛物线上， 设点 E 的坐标为（m，m）（ 0 2m  ），则 21 14m m   ． 解得 1 22 2 2 , 2 2 2m m     （舍去）． 所以 OE= 2 4 2 2m   ．所以 2 2 (2 2 2) 4 2 2EG GF EF m         ．所以 OE=EG． （3）设点 H 的坐标为（p，q）（ 0 2p  ， 0 2q  ）， 由 于 点 H 在 抛 物 线 21 14y x   上 ， 所 以 21 14q p   ， 即 2 4 4p q  ． 因 为 2 2 2 2 2 2 24 4 (2 )OH OI HI p q q q q         ， 所以 OH=2–q．所以 OK=OH=2–q．所以 CK=2－（2－q）=q=IH． 因为 CJ=OI， ∠OIH=∠JCK=90º，所以△OHI≌△JKC． 21、（2009 年贵州省黔东南州）凯里市某大型酒店有包房 100 间，在每天晚餐营业时间，每间包房收包房 费 100 元时，包房便可全部租出；若每间包房收费提高 20 元，则减少 10 间包房租出，若每间包房收费再 提高 20 元，则再减少 10 间包房租出，以每次提高 20 元的这种方法变化下去。 O A BC D E y xF G H I J K （第 24 题） （1）设每间包房收费提高 x（元），则每间包房的收入为 y1（元），但会减少 y2 间包房租出，请分别 写出 y1、y2 与 x 之间的函数关系式。 （2）为了投资少而利润大，每间包房提高 x（元）后，设酒店老板每天晚餐包房总收入为 y（元）， 请写出 y 与 x 之间的函数关系式，求出每间包房每天晚餐应提高多少元可获得最大包房费收入，并说明理 由。 【关键词】二次函数的应用 【答案】解：（1） xy  1001 ， xy 2 1 2  （2） )2 1100()100( xxy  ，即：y 11250)50(2 1 2  x 因为提价前包房费总收入为 100×100=10000。 当 x=50 时，可获最大包房收入 11250 元，因为 11250>10000。又因为每次提价为 20 元，所以每间包 房晚餐应提高 40 元或 60 元。 22、（2009 年贵州省黔东南州）已知二次函数 22  aaxxy 。 （1）求证：不论 a 为何实数，此函数图象与 x 轴总有两个交点。 （2）设 a<0，当此函数图象与 x 轴的两个交点的距离为 13 时，求出此二次函数的解析式。 （3）若此二次函数图象与 x 轴交于 A、B 两点，在函数图象上是否存在点 P，使得△PAB 的面积为 2 133 ， 若存在求出 P 点坐标，若不存在请说明理由。 【关键词】二次函数的综合应用 【答案】解（1）因为△= 04)2()2(4 22  aaa 所以不论 a 为何实数，此函数图象与 x 轴总有两个交点。 （2）设 x1、x2 是 022  aaxxy 的两个根，则 axx  21 ， 221  axx ，因两交点的 距离是 13 ，所以 13)(|| 2 2121  xxxx 。 即： 13)( 2 21  xx 变形为： 134)( 21 2 21  xxxx 所以： 13)2(4)( 2  aa 整理得： 0)1)(5(  aa 解方程得： 15  或a 又因为：a<0 所以：a=－1 所以：此二次函数的解析式为 32  xxy （3）设点 P 的坐标为 ),( 0yxo ，因为函数图象与 x 轴的两个交点间的距离等于 13 ，所以：AB= 13 所以：S△PAB= 2 13||2 1 0  yAB 所以： 2 13 2 ||13 0 y 即： 3|| 0 y ，则 30 y 30 y 时， 332 0  oxx ，即 0)2)(3( 0  oxx 解此方程得： 0x =－2 或 3 当 30 y 时， 332 0  oxx ，即 0)1(0 oxx 解此方程得： 0x =0 或 1 综上所述，所以存在这样的 P 点，P 点坐标是(－2,3), (3,3), (0, －3)或(1, －3)。 23、（2009 年江苏省）如图，已知二次函数 2 2 1y x x   的图象的顶点为 A ．二次函数 2y ax bx  的 图象与 x 轴交于原点O 及另一点C ，它的顶点 B 在函数 2 2 1y x x   的图象的对称轴上． （1）求点 A 与点C 的坐标； （2）当四边形 AOBC 为菱形时，求函数 2y ax bx  的关系式． 【关键词】待定系数法 【答案】解：（1） 2 22 1 ( 1) 2y x x x      ，所以顶点 A 的坐标为 (1 2)， ． （3 分） 因为二次函数 2y ax bx  的图象经过原点，且它的顶点在二次函数 2 2 1y x x   图象的对称轴l 上，所 以点 C 和点 O 关于直线 l 对称，所以点C 的坐标为 (2 0)， ． （2）因为四边形 AOBC 是菱形，所以点 B 和点 A 关于直线OC 对称，因此，点 B 的坐标为 (1 2)， ． 因为二次函数 2y ax bx  的图象经过点 B (1 2)， ， (2 0)C ， ，所以 2 4 2 0. a b a b       ， 解得 2 4 a b     ， ． 所以二次函数 2y ax bx  的关系式为 22 4y x x   ． 24、（2009 年浙江省绍兴市）定义一种变换：平移抛物线 1F 得到抛物线 2F ，使 2F 经过 1F 的顶点 A ．设 2F 的对称轴分别交 1 2F F， 于点 D B， ，点C 是点 A 关于直线 BD 的对称点． （1）如图 1，若 1F ： 2y x ，经过变换后，得到 2F ： 2y x bx  ，点C 的坐标为 (2 0)， ，则①b 的值等 于______________； ②四边形 ABCD 为（ ） A．平行四边形 B．矩形 C．菱形 D．正方形 （2）如图 2，若 1F ： 2y ax c  ，经过变换后，点 B 的坐标为 (2 1)c ， ，求 ABD△ 的面积； （3）如图 3，若 1F ： 21 2 7 3 3 3y x x   ，经过变换后， 2 3AC  ，点 P 是直线 AC 上的动点，求点 P 到点 D 的距离和到直线 AD 的距离之和的最小值． 【关键词】二次函数应用 【答案】 25、（2009 年吉林省）某数学研究所门前有一个边长为 4 米的正方形花坛，花坛内部要用红、黄、紫三种 颜色的花草种植成如图所示的图案，图案中 AE MN ．准备在形如 Rt AEH△ 的四个全等三角形内种植 红色花草，在形如 Rt AEH△ 的四个全等三角形内种植黄色花草，在正方形 MNPQ 内种植紫色花草，每 种花草的价格如下表： 品种 红色花草 黄色花草 紫色花草 价格（元/米 ） 60 80 120 设 AE 的长为 x 米，正方形 EFGH 的面积为 S 平方米，买花草所需的费用为W 元，解答下列问题： （1） S 与 x 之间的函数关系式为 S  ； （2）求W 与 x 之间的函数关系式，并求所需的最低费用是多少元； （3）当买花草所需的费用最低时，求 EM 的长． A B F C G D H Q P N M 红 黄 紫 E 【关键词】二次函数的极值问题、与二次函数有关的面积问题 【答案】解：（1） 2 2 2(4 ) 2 8 16.x x x x   或 （2） 60 4 AEB EFGN MNPQ MNPQW S S S  △ 正方形 正方形 正方形80( - S )+120 =60 2 2 2 214 (4 ) 80[ (4 ) ] 120 .2 x x x x x x        =80 2 160 1280.x x  配方，得 280( 1) 1200.W x   当 1x  时， 1200W 最小值 元． （3）设 EM a 米，则 ( 1)MH a  米 . 在 Rt EMH△ 中， 2 2 2 2( 1) 1 3 ,a a    解得 1 19 .2a   0, 19 1.2 a a     EM 的长为 19 1 2  米． 26、（2009 年深圳市）已知：Rt△ABC 的斜边长为 5，斜边上的高为 2，将这个直角三角形放置在平面直 角坐标系中，使其斜边 AB 与 x 轴重合（其中 OA0，n>0），连接 DP 交 BC 于点 E。 ①当△BDE 是等腰三角形时，直接写出．．．．此时点 E 的坐标。 ②又连接 CD、CP，△CDP 是否有最大面积？若有，求出△CDP 的最大面的最大面积和此时点 P 的坐标； 若没有，请说明理由。 【关键词】 【答案】（1）由 Rt△AOC∽Rt△COB 易知，CO2=OA.OB=OA(AB-OA),可求 OA=1,OB=4 ∴A(-1,0)B(4,0)C(0,2)可设解析式为 y=a(x+1)(x-4),将点 C(0,2)代入，可求 a= 1 2  ∴ 21 3 22 2y x x    为所求 （2） 1 1(3, )2E ； 2 4 8( , )5 5E 3 4 2(4 5, 5)5 5E  提示：直线 BC 的解析式为 1 22y x   设 ( , )E x y ， 利用勾股定理和点 ( , )E x y 在直线 BC 上，可得两个方程组 2 2 2 1 22 (2 ) 2 y x x y         2 2 2 1 22 (4 ) 2 y x x y         分别可求 2E 和 3E （3）过 D 作 X 轴的垂线，交 PC 于 M，易求 PC 的解析式为 2 2ny xm   ，且 2 4(2, 2)nM m   ， 故 图 11 2 2 1 ( )( )2 1 1 2 4( 2) 22 2 1 3( 2) 22 2 1 5 2 2 CDP CDM DMP P C M D P M S S S x x y y nx y m m nm m m m m m                         故，当 5 2m  时， 25 8CDPS  最大值 ， 5 21( , )2 8P 27、（2009 年台州市）如图，已知直线 1 12y x   交坐标轴于 BA， 两点，以线段 AB 为边向上作正方形 ABCD ，过点 CD，A， 的抛物线与直线另一个交点为 E ． （1）请直接写出点 DC, 的坐标； （2）求抛物线的解析式； （3）若正方形以每秒 5 个单位长度的速度沿射线 AB 下滑，直至顶点 D 落在 x 轴上时停止．设正方形落 在 x 轴下方部分的面积为 S ，求 S 关于滑行时间t 的函数关系式，并写出相应自变量t 的取值范围； （4）在（3）的条件下，抛物线与正方形一起平移，同时停止，求抛物线上 EC , 两点间的抛物线弧所扫 过的面积． 【关键词】与二次函数有关的面积问题 【答案】（1） )3,1(),2,3( DC ； （2）设抛物线为 cbxaxy  2 ，抛物线过 ),1,0( )3,1(),2,3( ，       .239 ,3 ,1 cba cba c 解得 5 ,6 17 ,6 1. a b c         ∴ 16 17 6 5 2  xxy ． （3）①当点 A 运动到点 F 时， ,1t 当 10  t 时，如图 1， ∵ 'OFA GFB   ， ,2 1tan  OF OAOFA ∴ ,2 1 5 ' ' ''tan  t GB FB GBGFB ∴ ,2 5' tGB  ∴ 2 ' 4 5 2 552 1''2 1 tttGBFBS GFB  ； ②当点C 运动到 x 轴上时， 2t ， 当 21  t 时，如图 2， O A B C D E y x 1 12y x   图 1 2 2' ' 2 1 5,A B AB    ∴ ,55'  tFA ∴ 2 55'  tGA ， ∵ 2 5' tHB  ， ∴ ' ' 1 ' ' ) ' '2A B HGS A G B H A B  梯形 （ 5)2 5 2 55(2 1  tt 4 5 2 5  t ； ③当点 D 运动到 x 轴上时， 3t ， 当 32  t 时，如图 3， ∵ 2 55'  tGA ， ∴ 2 553 2 555' ttGD  ， ∵ 1,1212 1  OAS AOF ， AOF ∽ 'GD H ∴ 2' )'( OA GD S S AOF HGD    ， ∴ 2 ' )2 553( tS HGD  ， ∴ 2 2 ' ' ' 3 5 55 )2GA B C H tS  五边形 （ ） （ = 4 25 2 15 4 5 2  tt ． （解法不同的按踩分点给分） （4）∵ 3t , 53''  AABB , ∴ ' ' ' 'BB C C AA D DS S S 阴影 矩形 矩形 = 'AAAD  = 15535  28、（2009 年宁波市）如图，抛物线 2 5 4y ax ax a   与 x 轴相交于点 A、B，且过点 (5 4)C ， ． （1）求 a 的值和该抛物线顶点 P 的坐标； （2）请你设计一种平移的方法，使平移后抛物线的顶点落在第二象限，并写出平移后抛物线的解析式． 【关键词】平移，二次函数 【答案】解：（1）把点 (5 4)C ， 代入抛物线 2 5 4y ax ax a   得， 图 4 图 3 A B P x y O C（5,4） 25 25 4 4a a a   ， 解得 1a  ． 该二次函数的解析式为 2 5 4y x x   ． 2 2 5 95 4 2 4y x x x         顶点坐标为 5 9 2 4P    ， ． （2）（答案不唯一，合理即正确） 如先向左平移 3 个单位，再向上平移 4 个单位， 得到的二次函数解析式为 2 25 9 1 73 42 4 2 4y x x                 ， 即 2 2y x x   ． 29、(2009 年义乌)如图，抛物线 2y ax bx c   与 x 轴的一个交点 A 在点（-2，0）和（-1，0）之间（包 括这两点），顶点 C 是矩形 DEFG 上（包括边界和内部）的一个 动点，则 (1)abc # 0 (填“  ”或“  ”)； (1)a 的取值范围是 # 【关键词】抛物线 2y ax bx c   系数的取值范围 【答案】（1）  （2） 3 2 4 25a ≤ ≤ 30、（2009 河池） 如图 12，已知抛物线 2 4 3y x x   交 x 轴于 A、B 两点，交 y 轴于点 C，抛物线的对称轴交 x 轴于点 E， 点 B 的坐标为（ 1 ，0）． （1）求抛物线的对称轴及点 A 的坐标； （2）在平面直角坐标系 xoy 中是否存在点 P， 与 A、B、C 三点构成一个平行四边形？若存在， 请写出点 P 的坐标；若不存在，请说明理由； （3）连结 CA 与抛物线的对称轴交于点 D，在抛物线上是否存在 点 M，使得直线 CM 把四边形 DEOC 分成面积相等的两部分？ 若存在，请求出直线 CM 的解析式；若不存在，请说明理由． 【关键词】二次函数、坐标、存在、面积 【答案】（1）① 对称轴 4 22x     ② 当 0y  时，有 2 4 3 0x x   解之，得 1 1x   ， 2 3x   ∴ 点 A 的坐标为（ 3 ，0）． （2）满足条件的点 P 有 3 个，分别为（ 2 ，3），（2，3），（ 4 ， 3 ）． （3）存在． O D B C A x y E 图 12 当 0x  时， 2 4 3 3y x x    ∴ 点 C 的坐标为（0，3） ∵ DE∥ y 轴，AO  3，EO  2，AE  1，CO  3 ∴ AED△ ∽ AOC△ ∴ AE DE AO CO  即 1 3 3 DE ∴ DE  1。 ∴ DEOCS 梯形 1 (1 3) 22     4 在 OE 上找点 F，使 OF  4 3 ，此时 COFS △ 1 4 32 3    2，直线 CF 把四边形 DEOC 分成面积相等的两部分，交抛物线于点 M． 设直线 CM 的解析式为 3y kx  ，它经过点 4 03F     ， ． 则 4 3 03 k   ， 解之，得 9 4k  ∴ 直线 CM 的解析式为 9 34y x  ， 31、（2009 柳州） 如图 11，已知抛物线 baxaxy  22 （ 0a ）与 x 轴的一个交点为 ( 1 0)B  ， ，与 y 轴的负半轴交于点 C，顶点为 D． （1）直接写出抛物线的对称轴，及抛物线与 x 轴的另一个交点 A 的坐标； （2）以 AD 为直径的圆经过点 C． ①求抛物线的解析式； ②点 E 在抛物线的对称轴上，点 F 在抛物线上， 且以 EFAB ，，， 四点为顶点的四边形为平行四边形，求点 F 的坐标． 【关键词】二次函数、对称轴、坐标、函数解析式、平行四边形 【答案】解：（1）对称轴是直线： 1x ， 点 A 的坐标是（3，0）． （说明：每写对 1 个给 1 分，“直线”两字没写不扣分） （2）如图 11，连接 AC、AD，过 D 作 轴 yDM  于点 M， 解法一：利用 AOC CMD△ ∽△ ∵点 A、D、C 的坐标分别是 A （3，0），D（1， ba  ）、 C（0， b ）， ∴AO＝3，MD=1． 由 MD OC CM AO  得 1 3 b a  ∴ 03  ab ， 又∵ baa  )1(2)1(0 2 ， ∴由      03 03 ba ab 得      3 1 b a ， ∴函数解析式为： 322  xxy ， 解法二：利用以 AD 为直径的圆经过点 C ∵点 A、D 的坐标分别是 A （3，0） 、D（1， ba  ）、C（0， b ）， O x y AB C D 图 11 ∴ 29 bAC  ， 21 aCD  ， 2)(4 baAD  ∵ 222 ADCDAC  ∴ 03  ab …① ， 又∵ baa  )1(2)1(0 2 …② ， 由①、②得 1 3a b ， ， ∴函数解析式为： 322  xxy ， （3）如图所示，当 BAFE 为平行四边形时 则 BA ∥ EF ，并且 BA ＝ EF ． ∵ BA =4，∴ EF =4 由于对称为 1x ， ∴点 F 的横坐标为 5． 将 5x 代入 322  xxy 得 12y ， ∴F（5，12）． 根据抛物线的对称性可知，在对称轴的左侧抛物线上也存在点 F，使得四边形 BAEF 是平行四边形，此时点 F 坐标为（ 3 ，12）． 当四边形 BEAF 是平行四边形时，点 F 即为点 D， 此时点 F 的坐标为（1， 4 ）． 综上所述，点 F 的坐标为（5，12）， （ 3 ，12）或（1， 4 ）． 32、(2009 烟台市) 如图，抛物线 2 3y ax bx   与 x 轴交于 A B， 两点，与 y 轴交于 C 点，且经过点 (2 3 )a， ，对称轴是直线 1x  ，顶点是 M ． （1） 求抛物线对应的函数表达式； （2） 经过 C,M 两点 作直线与 x 轴交 于点 N ，在 抛物线上 是否存在 这样的点 P ，使 以点 P A C N， ， ， 为顶点的四边形为平行四边形？若存在，请求出点 P 的坐标；若不存在，请说 明理由； （3） 设直线 3y x   与 y 轴的交点是 D ，在线段 BD 上任取一点 E （不与 B D， 重合），经过 A B E， ， 三点的圆交直线 BC 于点 F ，试判断 AEF△ 的形状，并说明理由； （4） 当 E 是直线 3y x   上任意一点时，（3）中的结论是否成立？（请直接写出结论）． O B x y A M C 1 3 【关键词】二次函数的综合应用 【答案】 解：（1）根据题意，得 3 4 2 3 1.2 a a b b a      ， 解得 1 2. a b     ， 抛物线对应的函数表达式为 2 2 3y x x   y xO AB C D 图 11 E F （2）存在． 在 2 2 3y x x   中，令 0x  ，得 3y   ． 令 0y  ，得 2 2 3 0x x   ， 1 21 3x x   ， ． ( 1 0)A  ， ， (3 0)B ， ， (0 3)C ， ． 又 2( 1) 4y x   ，顶点 (1 4)M ， ． 容易求得直线 CM 的表达式是 3y x   ． 在 3y x   中，令 0y  ，得 3x   ． ( 3 0)N  ， ， 2AN  ． 在 2 2 3y x x   中，令 3y   ，得 1 20 2x x ， ． 2CP AN CP   ， ． AN CP ∥ ，四边形 ANCP 为平行四边形，此时 (2 3)P ， ． （3） AEF△ 是等腰直角三角形． 理由：在 3y x   中，令 0x  ，得 3y  ，令 0y  ，得 3x  ． 直线 3y x   与坐标轴的交点是 (0 3)D ， ， (3 0)B ， ． OD OB  ， 45OBD  °． 又点 (0 3)C ， ， OB OC  ． 45OBC  °． 由图知 45AEF ABF    °， 45AFE ABE    °． 90EAF  °，且 AE AF ． AEF△ 是等腰直角三角形． （4）当点 E 是直线 3y x   上任意一点时，（3）中的结论成立． y x E D N OA C M P N1 F 33、（2009 恩施市）如图，在 ABC△ 中， 90 10A BC ABC  °， ，△ 的面积为 25，点 D 为 AB 边上的 任意一点（ D 不与 A 、B 重合），过点 D 作 DE BC∥ ，交 AC 于点 E ．设 DE x ，以 DE 为折线将 ADE△ 翻折（使 ADE△ 落在四边形 DBCE 所在的平面内），所得的 A DE△ 与梯形 DBCE 重叠部分的面积记为 y ． （1）用 x 表示 ADE△ 的面积； （2）求出 0 5x ≤ 时 y 与 x 的函数关系式； （3）求出5 10x  时 y 与 x 的函数关系式； （4）当 x 取何值时， y 的值最大？最大值是多少？ E A D B C A B C A 【关键词】相似、二次函数 【答案】解:(1) ∵ DE∥BC ∴∠ADE=∠B,∠AED=∠C ∴△ADE∽△ABC ∴ 2)( BC DE S S ABC ADE    即 2 4 1 xS ADE  (2)∵BC=10 ∴BC 边所对的三角形的中位线长为 5 ∴当 0﹤ 5x 时 2 4 1 xSy ADE   （3） x5 ﹤10 时，点 A'落在三角形的外部,其重叠部分为梯形 ∵S△A'DE=S△ADE= 2 4 1 x ∴DE 边上的高 AH=AH'= x2 1 由已知求得 AF=5 ∴A'F=AA'-AF=x-5 由△A'MN∽△A'DE 知 2 DEA' MNA' )HA' FA'(   S S 2 MNA' )5(  xS ∴ 25104 3)5(4 1 222  xxxxy （4）在函数 2 4 1 xy  中 ∵0﹤x≤5 ∴当 x=5 时 y 最大为： 4 25 在函数 25104 3 2  xxy 中 当 3 20 2  a bx 时 y 最大为： 3 25 ∵ 4 25 ﹤ 3 25 ∴当 3 20x 时，y 最大为： 3 25 N M F H E D C B A 34、1．（2009 年甘肃白银）［12 分+附加 4 分］如图 14（1），抛物线 2 2y x x k   与 x 轴交于 A、B 两点， 与 y 轴交于点 C（0， 3 ）．［图 14（2）、图 14（3）为解答备用图］ （1） k  ，点 A 的坐标为 ，点 B 的坐标为 ； （2）设抛物线 2 2y x x k   的顶点为 M，求四边形 ABMC 的面积； （3）在 x 轴下方的抛物线上是否存在一点 D，使四边形 ABDC 的面积最大？若存在，请求出点 D 的坐标； 若不存在，请说明理由； （4）在抛物线 2 2y x x k   上求点 Q，使△BCQ 是以 BC 为直角边的直角三角形． 图 14（1） 图 14（2） 图 14（3） 【关键词】抛物线顶点和对称轴 【答案】本小题满分 16 分(含附加 4 分) 图 14（１） 解：（1） 3k   ， A（-1，0）， B（3，0）． （2）如图 14（1），抛物线的顶点为 M（1，-4），连结 OM． 则 △AOC 的面积= 2 3 ，△MOC 的面积= 2 3 ， △MOB 的面积=6， ∴ 四边形 ABMC 的面积 =△AOC 的面积+△MOC 的面积+△MOB 的面积=9． 图 14（2） 说明：也可过点 M 作抛物线的对称轴，将四边形 ABMC 的面 积转化为求 1 个梯形与 2 个直角三角形面积的和． （3）如图 14（2），设 D（m， 322  mm ），连结 OD． 则 0＜m＜3， 322  mm ＜0． 且 △AOC 的面积= 2 3 ，△DOC 的面积= m2 3 ， △DOB 的面积=- 2 3 （ 322  mm ）， ∴ 四边形 ABDC 的面积=△AOC 的面积+△DOC 的面积+△DOB 的面积 = 62 9 2 3 2  mm = 8 75)2 3(2 3 2  m ． ∴ 存在点 D 3 15( )2 4 ， ，使四边形 ABDC 的面积最大为 8 75 ． （4）有两种情况： 图 14（3） 图 14（4） 如图 14（3），过点 B 作 BQ1⊥BC，交抛物线于点 Q1、交 y 轴于点 E，连接 Q1C． ∵ ∠CBO=45°，∴∠EBO=45°，BO=OE=3． ∴ 点 E 的坐标为（0，3）． ∴ 直线 BE 的解析式为 3y x   ． 由 2 3 2 3 y x y x x        ， 解得 1 1 2 5 x y ， ； ì =-ïïíï =ïî 2 2 3 0. x y ，ì =ïïíï =ïî ∴ 点 Q1 的坐标为（-2，5）．如图 14（4），过点 C 作 CF⊥CB，交抛物线于点 Q2、交 x 轴于点 F，连 接 BQ2． ∵ ∠CBO=45°，∴∠CFB=45°，OF=OC=3． ∴ 点 F 的坐标为（-3，0）． ∴ 直线 CF 的解析式为 3y x   ． 由 2 3 2 3 y x y x x        ， 解得 1 1 0 3 x y ， ； ì =ïïíï =-ïî 2 2 1 4 x y ， ． ì =ïïíï =-ïî ∴点 Q2 的坐标为（1，-4）． 综上，在抛物线上存在点 Q1（-2，5）、Q2（1，-4），使△BCQ1、△BCQ2 是以 BC 为直角边的直角三 角形． 说明：如图 14（4），点 Q2 即抛物线顶点 M，直接证明△BCM 为直角三角形同样得 2 分． 35、（2009 年甘肃庆阳）（10 分）图 19 是二次函数 21 22y x   的图象在 x 轴上方的一部分，若这段图 象与 x 轴所围成的阴影部分面积为 S，试求出 S 取值的一个范围． 图 19 【关键词】二次函数和抛物线有关概念 【答案】本小题满分 10 分 解：方法一： 由题意，可知这段图象与x轴的交点为A（-2，0）、B（2，0），与y轴的交点为C（0，2）． 显然，S在 ABC 面积与过A、B、C三点的⊙O半圆面积之间． ∵ ABCS△ =4， 1 2 OS = 2π， ∴ 4AD+CB，因此不存在某个位置，使四边形 A′B′CD 的周长最短． 第二种情况：设抛物线向左平移了 b 个单位，则点 A′和点 B′的坐标分别为 A′(-4-b，8)和 B′(2-b，2)． 因为 CD=2，因此将点 B′向左平移 2 个单位得 B′′(-b，2)， 要使 A′D+CB′最短，只要使 A′D+DB′′最短． 点 A′关于 x 轴对称点的坐标为 A′′(-4-b，-8)， 直线 A′′B′′的解析式为 5 5 22 2y x b   ． 要使 A′D+DB′′最短，点 D 应在直线 A′′B′′上，将点 D(-4，0)代入直线 A′′B′′的解析式，解得 16 5b  ． 故将抛物线向左平移时，存在某个位置，使四边形 A′B′CD 的周长最短，此时抛物线的函数解析式为 21 16( )2 5y x  ． 4 x2 2 A′ 8 -2O -2 -4 y 6 B′ CD -4 4 A′′ B′′ 51、（2009 年舟山）如图，已知点 A(-4，8)和点 B(2，n)在抛物线 2y ax 上． (1) 求 a 的值及点 B 关于 x 轴对称点 P 的坐标，并在 x 轴上找一点 Q，使得 AQ+QB 最短，求出点 Q 的坐 标； (2) 平移抛物线 2y ax ，记平移后点 A 的对应点为 A′，点 B 的对应点为 B′，点 C(-2，0)和点 D(-4，0)是 x 轴上的两个定点． ① 当抛物线向左平移到某个位置时，A′C+CB′ 最短，求此时抛物线的函数解析式； ② 当抛物线向左或向右平移时，是否存在某个位置，使四边形 A′B′CD 的周长最短？若存在，求出此时 抛物线的函数解析式；若不存在，请说明理由． 4 x2 2 A 8 -2O -2 -4 y 6 B CD -4 4 【关键词】二次函数的应用 【答案】解：(1) 将点 A(-4，8)的坐标代入 2y ax ，解得 1 2a  ． 将点 B(2，n)的坐标代入 21 2y x ，求得点 B 的坐标为(2，2)， 则点 B 关于 x 轴对称点 P 的坐标为(2，-2)． 直线 AP 的解析式是 5 4 3 3y x   ． 令 y=0，得 4 5x  ．即所求点 Q 的坐标是( 4 5 ，0)． 4 x2 2 A 8 -2O -2 -4 y 6 B CD -4 4 Q P (2)① 解法 1：CQ=︱-2- 4 5 ︱=14 5 ， 故将抛物线 21 2y x 向左平移 14 5 个单位时，A′C+CB′最短， 此时抛物线的函数解析式为 21 14( )2 5y x  ． 解法 2：设将抛物线 21 2y x 向左平移 m 个单位，则平移后 A′，B′的坐标分别为 A′(-4-m，8)和 B′(2-m，2)， 点 A′关于 x 轴对称点的坐标为 A′′(-4-m，-8)． 直线 A′′B′的解析式为 5 5 4 3 3 3y x m   ． 要使 A′C+CB′最短，点 C 应在直线 A′′B′上， 将点 C(-2，0)代入直线 A′′B′的解析式，解得 14 5m  ． 故将抛物线 21 2y x 向左平移 14 5 个单位时 A′C+CB′最短，此时抛物线的函数解析式为 21 14( )2 5y x  ． 4 x2 2 A′ 8 -2O -2 -4 y 6 B′ CD -4 4 A′′ ② 左右平移抛物线 21 2y x ，因为线段 A′B′和 CD 的长是定值，所以要使四边形 A′B′CD 的周长最短，只 要使 A′D+CB′最短； 第一种情况：如果将抛物线向右平移，显然有 A′D+CB′>AD+CB，因此不存在某个位置，使四边形 A′B′CD 的周长最短． 第二种情况：设抛物线向左平移了 b 个单位，则点 A′和点 B′的坐标分别为 A′(-4-b，8)和 B′(2-b，2)． 因为 CD=2，因此将点 B′向左平移 2 个单位得 B′′(-b，2)， 要使 A′D+CB′最短，只要使 A′D+DB′′最短． 点 A′关于 x 轴对称点的坐标为 A′′(-4-b，-8)， 直线 A′′B′′的解析式为 5 5 22 2y x b   ． 要使 A′D+DB′′最短，点 D 应在直线 A′′B′′上，将点 D(-4，0)代入直线 A′′B′′的解析式，解得 16 5b  ． 故将抛物线向左平移时，存在某个位置，使四边形 A′B′CD 的周长最短，此时抛物线的函数解析式为 21 16( )2 5y x  ． 4 x2 2 A′ 8 -2O -2 -4 y 6 B′ CD -4 4 A′′ B′′ 53、3.（2009 年广州市）如图 13，二次函数 )0(2  pqpxxy 的图象与 x 轴交于 A、B 两点， 与 y 轴交于点 C（0，-1），ΔABC 的面积为 4 5 。 （1）求该二次函数的关系式； （2）过 y 轴上的一点 M（0，m）作 y 轴上午垂线，若该垂线与ΔABC 的 外接圆有公共点，求 m 的取值范围； （3）在该二次函数的图象上是否存在点 D，使四边形 ABCD 为直角梯形？ 若存在，求出点 D 的坐标；若不存在，请说明理由。 54、（2009 年衡阳市）已知二次函数的图象过坐标原点，它的顶点坐标是（1， －2），求这个二次函数的关系式． 【关键词】二次函数解析式的求法 【答案】解：设这个二次函数的关系式为 2)1( 2  xay 得： 2)10(0 2  a 解得： 2a ∴这个二次函数的关系式是 2)1(2 2  xy ，即 xxy 42 2  55、（2009 年益阳市）阅读材料： 如图 12-1，过△ABC 的三个顶点分别作出与水平线垂直的三条直 线，外侧两条直线之间的距离叫△ABC 的“水平宽”(a)，中间的这条 直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h)”.我们可得出 一种计算三角形面积的新方法： ahS ABC 2 1 ，即三角形面积等于水 平宽与铅垂高乘积的一半. 解答下列问题： 如图 12-2，抛物线顶点坐标为点 C(1,4),交 x 轴于点 A(3,0)，交 y 轴于点 B. (1)求抛物线和直线 AB 的解析式； (2)点 P 是抛物线(在第一象限内)上的一个动点，连结 PA，PB，当 P 点运动到顶点 C 时，求△CAB 的铅垂高 CD 及 CABS ； (3)是否存在一点 P，使 S△PAB= 8 9 S△CAB，若存在，求出 P 点的坐标；若不存在，请说明理由. B C 铅垂高 水平宽 h a 图 12-1 A 2 图 12-2 x C O y A B D 1 1 【关键词】二次函数 【答案】解：(1)设抛物线的解析式为： 4)1( 2 1  xay . 把 A（3,0）代入解析式求得 1a 所以 324)1( 22 1  xxxy . 设直线 AB 的解析式为： bkxy 2 由 322 1  xxy 求得 B 点的坐标为 )3,0( . 把 )0,3(A ， )3,0(B 代入 bkxy 2 中 解得： 3,1  bk 所以 32  xy . (2)因为 C 点坐标为(１,4) 所以当 x＝１时，y1＝4，y2＝2 所以 CD＝4-2＝2. 3232 1 CABS (平方单位). (3)假设存在符合条件的点 P，设 P 点的横坐标为 x，△PAB 的铅垂高为 h， 则 xxxxxyyh 3)3()32( 22 21  . 由 S△PAB= 8 9 S△CAB 得： 38 9)3(32 1 2  xx 化简得： 09124 2  xx 解得， 2 3x 将 2 3x 代入 322 1  xxy 中， 解得 P 点坐标为 )4 15,2 3( 56、（2009 年济宁市）某体育用品商店购进一批滑板，每件进价为 100 元，售价为 130 元，每星期可卖出 80 件.商家决定降价促销，根据市场调查，每降价 5 元，每星期可多卖出 20 件. （1）求商家降价前每星期的销售利润为多少元？ （2）降价后，商家要使每星期的销售利润最大，应将售价定为多少元？最大销售利润是多少？ 【关键词】二次函数的实际应用 【答案】解：(1) （130-100）×80=2400（元）； （2）设应将售价定为 x 元，则销售利润 130( 100)(80 20)5 xy x     24 1000 60000x x    24( 125) 2500x    .当 125x  时， y 有最 大值 2500.∴应将售价定为 125 元,最大销售利润是 2500 元. 57、（2009 年日照）某仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施．该设 施的下部 ABCD 是矩形，其中 AB=2 米，BC=1 米；上部 CDG 是等边三角形，固定点 E 为 AB 的中点．△ EMN 是由电脑控制其形状变化的三角通风窗（阴影部分均不通风），MN 是可以沿设施边框上下滑动且始 终保持和 AB 平行的伸缩横杆． （1）当 MN 和 AB 之间的距离为 0.5 米时，求此时△EMN 的面积； （2）设 MN 与 AB 之间的距离为 x 米，试将△EMN 的面积 S（平方米）表示成关于 x 的函数； （3）请你探究△EMN 的面积 S（平方米）有无最大值，若有，请求出这个最大值；若没有，请说明理由． EA B G N D M C （第 23 题图） 【关键词】二次函数的极值问题, 二次函数的应用, 相似三角形判定和性质 【答案】 解：（1）由题意，当 MN 和 AB 之间的距离为 0.5 米时，MN 应位于 DC 下方，且此时△EMN 中 MN 边上 的高为 0.5 米. 所以，S△EMN= 5.022 1  =0.5（平方米）. 即△EMN 的面积为 0.5 平方米. （2）①如图 1 所示，当 MN 在矩形区域滑动， 即 0＜x≤1 时， △EMN 的面积 S= x 22 1 = x ； ②如图 2 所示，当 MN 在三角形区域滑动， 即 1＜x＜ 31 时， 如图，连接 EG，交 CD 于点 F，交 MN 于点 H， ∵ E 为 AB 中点， ∴ F 为 CD 中点，GF⊥CD,且 FG＝ 3 . 又∵ MN∥CD， ∴ △MNG∽△DCG． ∴ GF GH DC MN  ，即 2[ 3 1 ] 3 xMN   ． 故△EMN 的面积 S＝ 1 2[ 3 1 ] 2 3 x x   ＝ xx )3 31(3 3 2  ； 综合可得： E N EB B G D M A B C 图 1 EA B G N D M C 图 2 H F                  3113 313 3 10 2 ＜＜． ＜， xxx xx S （3）①当 MN 在矩形区域滑动时， xS  ，所以有 10  S ； ②当 MN 在三角形区域滑动时，S= xx )3 31(3 3 2  . 因而，当 2 31 2  a bx （米）时,S 得到最大值， 最大值 S= a bac 4 4 2 = ）（ ）（ 3 34 3 31 2   = 3 3 2 1  （平方米）. ∵ 13 3 2 1  ， ∴ S 有最大值，最大值为 3 3 2 1  平方米. 58、（2009 年福州）已知直线 l：y=－x+m（m≠0）交 x 轴、y 轴于 A、B 两点，点 C、M 分别在 线段 OA、AB 上，且 OC=2CA，AM=2MB，连接 MC，将△ACM 绕点 M 旋转 180°，得到△FEM，则点 E 在 y 轴上, 点 F 在直线 l 上;取线段 EO 中点 N,将 ACM 沿 MN 所在直 线翻折，得到△PMG，其中 P 与 A 为对称点.记：过点 F 的双曲线为 1C ， 过点 M 且以 B 为顶点的抛物线为 2C ，过点 P 且以 M 为顶点的抛物线 为 3C . (1) 如图 10，当 m=6 时，①直接写出点 M、F 的坐标，②求 1C 、 2C 的 函数解析式； （2）当 m 发生变化时， ①在 1C 的每一支上，y 随 x 的增大如何变化？ 请说明理由。 ②若 2C 、 3C 中的 y 都随着 x 的增大而减小,写出 x 的取值范围。 【关键词】相似三角形,用待定系数法求反比例函数和二次函数解析式, 函数增减性. 【答案】（１）①点Ｍ的坐标为（２，４），点Ｆ的坐标为（－２，８）． 2 设 1C 的函数解析式为 x ky  （ )0k ． ∵ 1C 过点Ｆ（－２，８） ∴ 1C 的函数解析式为 xy 16 ． ∵ 2C 的顶点Ｂ的坐标是（０，６）, ∴设 2C 的函数解析式为 2 6( 0)y ax a   ． ∵ 2C 过点 M（2，4）, ∴ 464 a . 2 1a ． ∴ 2C 的函数解析式为 62 1 2  xy ． （2）依题意得，A（m，０），B（０，m）， 图 10 ∴点Ｍ坐标为（ mm 3 2,3 1 ），点Ｆ坐标为（ m3 1 ， m3 4 ）． ①设 1C 的函数解析式为 ky x  （ )0k ． ∵ 1C 过点Ｆ（ m3 1 ， m3 4 ）, ∴ 2 9 4 mk  ． ∵ 0m ,∴ 0k  . ∴在 1C 的每一支上，y 随着 x 的增大而增大． ②答：当 m ＞０时，满足题意的 x 的取值范围为 0＜x＜ m3 1 ； 当 m ＜０时，满足题意的 x 的取值范围为 m3 1 ＜x＜０． 59、（2009 年宜宾）如图，在平面直角坐标系 x O y 中，等腰梯形 OABC 的下底边 OA 在 x 的正半轴上，BC ∥OA，OC=AB，tan∠BAO= 3 4 ,点 B 的坐标为（7，4）。 （1）求 A、C 的坐标； （2）求经过点 O、B、C 的抛物线的解析式； （3）在第一象限内（2）中的抛物线上是否存在一点 P，使得经过点 P 且与等腰梯形一腰平行的直线将该 梯形分成面积相等的两个部分？若存在，请求出点 P 的横坐标；若不存在，请说明理由． HG 【关键词】正切，坐标的意义，求二次函数解析式，求一次函数解析式，梯形和平行四边形的面积，一元 二次方程，两直线平行时解析式的特征 【答案】(1)过点 B 作 BH⊥OA, 过点 C 作 CG⊥OA,垂足分别为 H、G.得△OCG≌△ABH. ∵tan∠BAO= 3 4 ,∴ AH BH = 3 4 . ∵点 B 的坐标为（7，4）,∴BH=4,AH=3. ∴CG=BH=4,OG=AH=3. ∴点 A 的坐标是(10,0),点 C 的坐标是(3,4). (2) 设经过点 O、B、C 的抛物线的解析式为 cbxaxy  2 ,则       .439 4749 0 cba cba c ， ， 解得 a= 21 4 ,b= 21 40 ,c=0. ∴ xxy 21 40 21 4 2  . (也可以利用抛物线的对称性求解析式) (3)直线 AB 的解析式是 3 40 3 4  xy ,直线 OC 的解析式是 xy 3 4 . S 梯形 OABC=28， 若经过点 P 且与等腰梯形 OABC 腰 AB 平行的直线解析式是 mxy  3 4 ，该直线交 OA、BC 于点 M、N， ∵S 平行四边形 MABN= 3 4 S 梯形 OABC =14，∴BN= 4 14 = 2 7 .∴点 N 的坐标是( 2 7 ,4). 将( 2 7 ,4)代入 mxy  3 4 ,得 m= 3 26 .联立        .21 40 21 4 3 26 3 4 2 xxy xy ， 消去 y,得 091342 2  xx ,x= 2 10717  . 若经过点 P 且与等腰梯形 OABC 腰 OC 平行的直线解析式是 nxy  3 4 ，该直线交 OA、BC 于点 K、L， ∵S 平行四边形 OKLC= 3 4 S 梯形 OABC =14，∴OK= 4 14 = 2 7 .∴点 K 的坐标是( 2 7 ,0). 将( 2 7 ,0)代入 nxy  3 4 ,得 n=- 3 14 .联立        .21 40 21 4 3 14 3 4 2 xxy xy ， 消去 y,得 04962 2  xx , x= 2 1073  . HG HG 60、（2009 年福州）如图 9，等边 ABC 边长为 4，E 是边 BC 上动点， ACEH  于 H，过 E 作 EF ∥ AC ， 交线段 AB 于点 F ，在线段 AC 上取点 P ，使 EBPE  。设 )20(  xxEC 。 （1） 请直接写出图中与线段 EF 相等的两条线段（不再另外添加辅助线）； （2） Q 是线段 AC 上的动点，当四边形 EFPQ 是平行四边形时,求□EFPQ 的面积（用含 x 的代数式表 示）； （3） 当（2）中 的□EFPQ 面积最大值时，以 E 为圆心， r 为半径作圆，根据⊙E 与此时□EFPQ 四条 边交点的总个数，求相应的 r 的取值范围。 【关键词】二次函数的极值,图形中的二次函数,菱形判定, 直线与圆 的位置关系,分类讨论思想 【答案】（１）ＢＥ、ＰＥ、BF 三条线段中任选两条． （２）在Ｒt△ＣHＥ中，∠CHE＝9０°,∠Ｃ＝６０°， ∴ＥH＝ 3 2 x . ∵PQ=EF=BE=4-x, ∴ 23 2 32EFPQS x x   ． （３） 2 2 3 2 32 3 ( 2) 2 32 EFPQS x x x         ∴当 x＝２时， EFPQS 有最大值． 此时 E、F、P 分别为△ABC 三边 BC、AB、AC 的中点，且点 C、 点 Q 重合 ∴平行四边形 EFPQ 是菱形． 过Ｅ点作ＥD⊥ＦＰ于 D， ∴ＥD＝ＥH＝ 3 ． ∴当⊙E 与□EFPQ 四条边交点的总个数是２个时，０＜r＜ 3 ； 当⊙E 与□EFPQ 四条边交点的总个数是４个时，r＝ 3 ； 当⊙E 与□EFPQ 四条边交点的总个数是６个时， 3 ＜r＜２； 当⊙E 与□EFPQ 四条边交点的总个数是３个时，r＝２时； 当⊙E 与□EFPQ 四条边交点的总个数是０个时，r＞２时． 61、（2009 年重庆）某电视机生产厂家去年销往农村的某品牌电视机每台的售价 y（元）与月份 x 之间满足 函数关系 50 2600y x   ，去年的月销售量 p（万台）与月份 x 之间成一次函数关系，其中两个月的销 售情况如下表： 月份 1 月 5 月 销售量 3.9 万台 4.3 万台 （1）求该品牌电视机在去年哪个月销往农村的销售金额最大？最大是多少？ （2）由于受国际金融危机的影响，今年 1、2 月份该品牌电视机销往农村的售价都比去年 12 月份下降了 %m ，且每月的销售量都比去年 12 月份下降了 1.5m%．国家实施“家电下乡”政策，即对农村家庭购买 新的家电产品，国家按该产品售价的 13%给予财政补贴．受此政策的影响，今年 3 至 5 月份，该厂家销往 农村的这种电视机在保持今年 2 月份的售价不变的情况下，平均每月的销售量比今年 2 月份增加了 1.5 万 台．若今年 3 至 5 月份国家对这种电视机的销售共给予了财政补贴 936 万元，求 m 的值（保留一位小数）． （参考数据： 34 5.831≈ ， 35 5.916≈ ， 37 6.083≈ ， 38 6.164≈ ） 【关键词】确定一次函数解析式, 二次函数的极值问题, 一元二次方程的应用 【答案】(1)设去年的月销售量 p（万台）与月份 x 之间的一次函数关系是 bkxp  ,根据题意,得      .53.4 ,9.3 bk bk 解得      .8.3 ,1.0 b k ∴ 8.31.0  xp . 设该品牌电视机在农村的销售金额为 w 万元,则 )260050)(8.31.0(  xxpyw = 9880705 2  xx = 10125)7(5 2  x ∴该品牌电视机在去年 7 月销往农村的销售金额最大,最大是 10125 万元. (2)当 12x 时, 2000y , 5p . 根据题意,列方程,得   9363%135.1%)5.11(5%)1(2000  mm 整理,得 053%)(14%)(75 2  mm . 解得 115 3714% m (舍去)或 528.015 3714% m .所以 m 的值是 52.8. 62、（2009 年重庆）已知：如图，在平面直角坐标系 xOy 中，矩形 OABC 的边 OA 在 y 轴的正半轴上，OC 在 x 轴的正半轴上，OA=2，OC=3．过原点 O 作∠AOC 的平分线交 AB 于点 D，连接 DC，过点 D 作 DE ⊥DC，交 OA 于点 E． （1）求过点 E、D、C 的抛物线的解析式； （2）将∠EDC 绕点 D 按顺时针方向旋转后，角的一边与 y 轴的正半轴交于点 F，另一边与线段 OC 交于 点 G．如果 DF 与（1）中的抛物线交于另一点 M，点 M 的横坐标为 6 5 ，那么 EF=2GO 是否成立？若成立， 请给予证明；若不成立，请说明理由； （3）对于（2）中的点 G，在位于第一象限内的该抛物线上是否存在点 Q，使得直线 CQ 与 AB 的交点 P 与点 C、G 构成的△PCG 是等腰三角形？若存在，请求出点 Q 的坐标；若不存在，请说明理由． 【关键词】全等三角形,矩形,待定系数法求二次函数解析式, 分类讨论思想 【答案】解：（1）由已知，得 (3 0)C ， ， (2 2)D ， ， 90ADE CDB BCD      ° ， 1tan 2 tan 2 12AE AD ADE BCD         ．  (01)E ， ． 设过点 E D C、 、 的抛物线的解析式为 2 ( 0)y ax bx c a    ． 将点 E 的坐标代入，得 1c  ． 将 1c  和点 D C、 的坐标分别代入，得 4 2 1 2 9 3 1 0. a b a b        ， 解这个方程组，得 5 6 13 6 a b      故抛物线的解析式为 25 13 16 6y x x    ． （2） 2EF GO 成立． 点 M 在该抛物线上，且它的横坐标为 6 5 ， 点 M 的纵坐标为12 5 ． 设 DM 的解析式为 1( 0)y kx b k   ， 将点 D M、 的坐标分别代入，得 1 1 2 2 6 12 .5 5 k b k b     ， 解得 1 1 2 3 k b      ， ．  DM 的解析式为 1 32y x   ．  (0 3)F ， ， 2EF  ． 过点 D 作 DK OC⊥ 于点 K ， 则 DA DK ． 90ADK FDG    °， FDA GDK   ． 又 90FAD GKD    °， DAF DKG△ ≌△ ． 1KG AF   ． 1GO  ． 2EF GO  ． （3）点 P 在 AB 上， (1 0)G ， ， (3 0)C ， ，则设 (1 2)P ， ．  2 2 2( 1) 2PG t   ， 2 2 2(3 ) 2PC t   ， 2GC  ． ①若 PG PC ，则 2 2 2 2( 1) 2 (3 ) 2t t     ， 解得 2t  ． (2 2)P ， ，此时点Q 与点 P 重合．  (2 2)Q ， ． ②若 PG GC ，则 2 2( 1) 2 2t    ， 解得 1t  ， (1 2)P ， ，此时GP x⊥ 轴． GP 与该抛物线在第一象限内的交点 Q 的横坐标为 1， 点Q 的纵坐标为 7 3 ．  71 3Q     ， ． ③若 PC GC ，则 2 2 2(3 ) 2 2t   ， 解得 3t  ， (3 2)P ， ，此时 2PC GC  ， PCG△ 是等腰直角三角形． 过点 Q 作QH x⊥ 轴于点 H ， 则QH GH ，设QH h ， ( 1 )Q h h  ， ． 25 13( 1) ( 1) 16 6h h h      ． 解得 1 2 7 25h h  ， （舍去）． 12 7 5 5Q     ， ． 综上所述，存在三个满足条件的点Q ， y x D B C A EE O ＭF KGG y x D B C A EE O Q P HGG (P) (Q) Q (P) 即 (2 2)Q ， 或 71 3Q     ， 或 12 7 5 5Q     ， ． 63、3（2009 年广西钦州）如图，已知抛物线 y＝ 3 4 x2＋bx＋c 与坐标轴交于 A、B、C 三点， A 点的坐标为（－1，0），过点 C 的直线 y＝ 3 4t x－3 与 x 轴交于点 Q，点 P 是线段 BC 上的一个动点，过 P 作 PH⊥OB 于点 H．若 PB＝5t，且 0＜t＜1． （1）填空：点 C 的坐标是_▲_，b＝_▲_，c＝_▲_； （2）求线段 QH 的长（用含 t 的式子表示）； （3）依点 P 的变化，是否存在 t 的值，使以 P、H、Q 为顶点的三角形与 △COQ 相似？若存在，求出所有 t 的值；若不存在，说明理由． 【关键词】二次函数、一次函数、相似三角形. 【答案】 解：（1）（0，－3），b＝－ 9 4 ，c＝－3． （2）由（1），得 y＝ 3 4 x2－ 9 4 x－3，它与 x 轴交于 A，B 两点，得 B（4， 0）． ∴OB＝4，又∵OC＝3，∴BC＝5． 由题意，得△BHP∽△BOC， ∵OC∶OB∶BC＝3∶4∶5， ∴HP∶HB∶BP＝3∶4∶5， ∵PB＝5t，∴HB＝4t，HP＝3t． ∴OH＝OB－HB＝4－4t． 由 y＝ 3 4t x－3 与 x 轴交于点 Q，得 Q（4t，0）． ∴OQ＝4t． ①当 H 在 Q、B 之间时， QH＝OH－OQ ＝（4－4t）－4t＝4－8t． ②当 H 在 O、Q 之间时， QH＝OQ－OH ＝4t－（4－4t）＝8t－4． 综合①，②得 QH＝｜4－8t｜； （3）存在 t 的值，使以 P、H、Q 为顶点的三角形与△COQ 相似． ①当 H 在 Q、B 之间时，QH＝4－8t， 若△QHP∽△COQ，则 QH∶CO＝HP∶OQ，得 4 8 3 t ＝ 3 4 t t ， ∴t＝ 7 32 ． 若△PHQ∽△COQ，则 PH∶CO＝HQ∶OQ，得 3 3 t ＝ 4 8 4 t t  ， 即 t2＋2t－1＝0． ∴t1＝ 2 －1，t2＝－ 2 －1（舍去）． ②当 H 在 O、Q 之间时，QH＝8t－4． 若△QHP∽△COQ，则 QH∶CO＝HP∶OQ，得 8 4 3 t  ＝ 3 4 t t ， ∴t＝ 25 32 ． 若△PHQ∽△COQ，则 PH∶CO＝HQ∶OQ，得 3 3 t ＝ 8 4 4 t t  ， 即 t2－2t＋1＝0． ∴t1＝t2＝1（舍去）． 综上所述，存在t 的值，t1＝ 2 －1，t2＝ 7 32 ，t3＝ 25 32 ． 4.（2009 年广西梧州）如图（9）-1，抛物线 2 3y ax ax b   经过 A（ 1 ，0），C（3， 2 ）两点， 与 y 轴交于点 D，与 x 轴交于另一点 B． （1）求此抛物线的解析式； （2）若直线 )0(1  kkxy 将四边形 ABCD 面积二等分，求 k 的值； D O BA x y C y=kx+1 （3）如图（9）-2，过点 E（1，1）作 EF⊥ x 轴于点 F，将△AEF 绕平面内某点 旋转 180°得△MNQ（点 M、N、Q 分别与点 A、E、F 对应），使点 M、N 在抛物线上，作 MG⊥ x 轴于点 G， 若线段 MG︰AG＝1︰2，求点 M，N 的坐标． E F M N G O BA x y Q 【关键词】二次函数、待定系数法、一元二次方程、四边形. 【答案】 （1）解：把 A（ 1 ，0），C（3， 2 ）代入抛物线 2 3y ax ax b   得      299 0)1(3)1( 2 baa baa 整理得      2 04 b ba 解得      2 2 1 b a ∴抛物线的解析式为 22 3 2 1 2  xxy （2）令 022 3 2 1 2  xx 解得 1 21 4x x  ， ∴ B 点坐标为（4，0） D O BA x y C B y=kx+1 H T 又∵D 点坐标为（0， 2 ） ∴AB∥CD ∴四边形 ABCD 是梯形． ∴S 梯形 ABCD ＝ 82)35(2 1  设直线 )0(1  kkxy 与 x 轴的交点为 H， 与 CD 的交点为 T， 则 H（ k 1 ，0）， T（ k 3 ， 2 ） ∵直线 )0(1  kkxy 将四边形 ABCD 面积二等分 E F M N G O BA x y Q ∴S 梯形 AHTD ＝ 2 1 S 梯形 ABCD＝４ ∴ 42)311(2 1  kk ∴ 3 4k （3）∵MG⊥ x 轴于点 G，线段 MG︰AG＝1︰2 ∴设 M（m， 2 1 m ）， ∵点 M 在抛物线上 ∴ 22 3 2 1 2 1 2  mmm 解得 1 23 1m m  ， （舍去） ∴M 点坐标为（3， 2 ）根据中心对称图形性质知，MQ∥AF，MQ＝AF，NQ＝EF， ∴N 点坐标为（1， 3 ） 5. (2009 年甘肃定西)如图 14（1），抛物线 2 2y x x k   与 x 轴交于 A、B 两点，与 y 轴交于点 C（0， 3 ）．［图 14（2）、图 14（3）为解答备用图］ （1） k  ，点 A 的坐标为 ，点 B 的坐标为 ； （2）设抛物线 2 2y x x k   的顶点为 M，求四边形 ABMC 的面积； （3）在 x 轴下方的抛物线上是否存在一点 D，使四边形 ABDC 的面积最大？若存在，请求出点 D 的坐标； 若不存在，请说明理由； （4）在抛物线 2 2y x x k   上求点 Q，使△BCQ 是以 BC 为直角边的直角三角形． 【关键词】一次函数、二次函数、待定系数法、一元二次方程、四边形. 【答案】 解：（1） 3k   ， A（-1，0）， B（3，0）． （2）如图 14（1），抛物线的顶点为 M（1，-4），连结 OM． 则 △AOC 的面积= 2 3 ，△MOC 的面积= 2 3 ， △MOB 的面积=6， ∴ 四边形 ABMC 的面积 =△AOC 的面积+△MOC 的面积+△MOB 的面积=9． 说明：也可过点 M 作抛物线的对称轴，将四边形 ABMC 的面 积转化为求 1 个梯形与 2 个直角三角形面积的和． （3）如图 14（2），设 D（m， 322  mm ），连结 OD． 则 0＜m＜3， 322  mm ＜0． 且 △AOC 的面积= 2 3 ，△DOC 的面积= m2 3 ， △DOB 的面积=- 2 3 （ 322  mm ）， ∴ 四边形 ABDC 的面积=△AOC 的面积+△DOC 的面积+△DOB 的面积 = 62 9 2 3 2  mm = 8 75)2 3(2 3 2  m ． ∴ 存在点 D 3 15( )2 4 ， ，使四边形 ABDC 的面积最大为 8 75 ． （4）有两种情况： 图 14（2） 如图 14（3），过点 B 作 BQ1⊥BC，交抛物线于点 Q1、交 y 轴于点 E，连接 Q1C． ∵ ∠CBO=45°，∴∠EBO=45°，BO=OE=3． ∴ 点 E 的坐标为（0，3）． ∴ 直线 BE 的解析式为 3y x   ． 由 2 3 2 3 y x y x x        ， 解得 1 1 2 5 x y ， ； ì =-ïïíï =ïî 2 2 3 0. x y ，ì =ïïíï =ïî ∴ 点 Q1 的坐标为（-2，5）． 如图 14（4），过点 C 作 CF⊥CB，交抛物线于点 Q2、交 x 轴于点 F，连接 BQ2． ∵ ∠CBO=45°，∴∠CFB=45°，OF=OC=3． ∴ 点 F 的坐标为（-3，0）． ∴ 直线 CF 的解析式为 3y x   ． 由 2 3 2 3 y x y x x        ， 解得 1 1 0 3 x y ， ； ì =ïïíï =-ïî 2 2 1 4 x y ， ． ì =ïïíï =-ïî ∴点 Q2 的坐标为（1，-4）． 综上，在抛物线上存在点 Q1（-2，5）、Q2（1，-4），使△BCQ1、△BCQ2 是以 BC 为直角边的直角三 角形． 说明：如图 14（4），点 Q2 即抛物线顶点 M，直接证明△BCM 为直角三角形同样得 2 分． 66、2009 年包头）某商场试销一种成本为每件 60 元的服装，规定试销期间销售单价不低于成本单价，且 获利不得高于 45%，经试销发现，销售量 y（件）与销售单价 x（元）符合一次函数 y kx b  ，且 65x  时， 55y  ； 75x  时， 45y  ． （1）求一次函数 y kx b  的表达式； （2）若该商场获得利润为W 元，试写出利润W 与销售单价 x 之间的关系式；销售单价定为多少元时，商 场可获得最大利润，最大利润是多少元？ （3）若该商场获得利润不低于 500 元，试确定销售单价 x 的范围． 【关键词】一次函数、二次函数、最大值 解：（1）根据题意得 65 55 75 45. k b k b      ， 解得 1 120k b  ， ． 所求一次函数的表达式为 120y x   ．······················································· （2 分） （2） ( 60) ( 120)W x x    2 180 7200x x    2( 90) 900x    ，······································································ （4 分） 抛物线的开口向下，当 90x  时，W 随 x 的增大而增大， 而 60 87x≤ ≤ ， 当 87x  时， 2(87 90) 900 891W      ． 当销售单价定为 87 元时，商场可获得最大利润，最大利润是 891 元．··············（6 分） （3）由 500W  ，得 2500 180 7200x x    ， 整理得， 2 180 7700 0x x   ，解得， 1 270 110x x ， ．···························· （7 分） 由图象可知，要使该商场获得利润不低于 500 元，销售单价应在 70 元到 110 元之间，而 60 87x≤ ≤ ， 所以，销售单价 x 的范围是 70 87x≤ ≤ ．·················································· （10 分） （2009 年包头）已知二次函数 2y ax bx c   （ 0a  ）的图象经过点 (1 0)A ， ， (2 0)B ， ， (0 2)C ， ，直 线 x m （ 2m  ）与 x 轴交于点 D ． （1）求二次函数的解析式； （2）在直线 x m （ 2m  ）上有一点 E （点 E 在第四象限），使得 E D B、 、 为顶点的三角形与以 A O C、 、 为顶点的三角形相似，求 E 点坐标（用含 m 的代数式表示）； （3）在（2）成立的条件下，抛物线上是否存在一点 F ，使得四边形 ABEF 为平行四边形？若存在，请 求出 m 的值及四边形 ABEF 的面积；若不存在，请说明理由． y xO 【关键词】二次函数、相似三角形、运动变化、抛物线 解：（1）根据题意，得 0 4 2 0 2. a b c a b c c           ， ， 解得 1 3 2a b c    ， ， ． y xO BA D C (x=m) (F2)F1 E1 (E2) 2 3 2y x x     ．··························· （2 分） （2）当 EDB AOC△ ∽△ 时， 得 AO CO ED BD  或 AO CO BD ED  ， ∵ 1 2 2AO CO BD m   ， ， ， 当 AO CO ED BD  时，得 1 2 2ED m   ， ∴ 2 2 mED  ， ∵点 E 在第四象限，∴ 1 2 2 mE m      ， ．························································ （4 分） 当 AO CO BD ED  时，得 1 2 2m ED  ，∴ 2 4ED m  ， ∵点 E 在第四象限，∴ 2 ( 4 2 )E m m， ．························································ （6 分） （3）假设抛物线上存在一点 F ，使得四边形 ABEF 为平行四边形，则 1EF AB  ，点 F 的横坐标为 1m  ， 当点 1E 的坐标为 2 2 mm      ， 时，点 1F 的坐标为 21 2 mm     ， ， ∵点 1F 在抛物线的图象上， ∴ 22 ( 1) 3( 1) 22 m m m       ， ∴ 22 11 14 0m m   ， ∴ (2 7)( 2) 0m m   ， ∴ 7 22m m ， （舍去）， ∴ 1 5 3 2 4F     ， ， ∴ 3 31 4 4ABEFS    ．··············································································（9 分） 当点 2E 的坐标为 ( 4 2 )m m， 时，点 2F 的坐标为 ( 1 4 2 )m m ， ， ∵点 2F 在抛物线的图象上， ∴ 24 2 ( 1) 3( 1) 2m m m       ， ∴ 2 7 10 0m m   ， ∴ ( 2)( 5) 0m m   ，∴ 2m  （舍去）， 5m  ， ∴ 2 (4 6)F ， ， ∴ 1 6 6ABEFS    ．··············································································（12 分） 注：各题的其它解法或证法可参照该评分标准给分． （2009 年长沙）如图，二次函数 2y ax bx c   （ 0a  ）的图象与 x 轴交于 A B、 两点，与 y 轴相交于 点C ．连结 AC BC A C、 ， 、 两点的坐标分别为 ( 3 0)A  ， 、 (0 3)C ， ，且当 4x   和 2x  时二次函数的 函数值 y 相等． （1）求实数 a b c， ， 的值； （2）若点 M N、 同时从 B 点出发，均以每秒 1 个单位长度的速度分别沿 BA BC、 边运动，其中一个点到 达终点时，另一点也随之停止运动．当运动时间为 t 秒时，连结 MN ，将 BMN△ 沿 MN 翻折，B 点恰好 落在 AC 边上的 P 处，求t 的值及点 P 的坐标； （3）在（2）的条件下，二次函数图象的对称轴上是否存在点 Q ，使得以 B N Q， ， 为项点的三角形与 ABC△ 相似？如果存在，请求出点 Q 的坐标；如果不存在，请说明理由． y O x C N B P MA 【关键词】二次函数、运动变化、相似、存在性 68、（2009 年莆田）已知，如图 1，过点  0 1E ， 作平行于 x 轴的直线l ，抛物线 21 4y x 上的两点 A B、 的横坐标分别为  1 和 4，直线 AB 交 y 轴于点 F ，过点 A B、 分别作直线l 的垂线，垂足分别为点C 、 D ，连接CF DF、 ． （1）求点 A B F、 、 的坐标； （2）求证： CF DF ； E DC AF B xO y l E DC O F x y （图 1） 备用图 （ 3 ） 点 P 是 抛 物 线 21 4y x 对称轴右侧图象上的一动点，过点 P 作 PQ PO⊥ 交 x 轴于点 Q ，是否存在点 P 使得 OPQ△ 与 CDF△ 相似？若存在，请求出所有符合条件的点 P 的坐标；若不存在，请说明理由． 【关键词】二次函数、抛物线、一次函数、相似三角形 （1）解:方法一，如图 1，当 1x   时, 1 4y  当 4x  时, 4y  E DC AF B xO y l （图 1） ∴ 1A    1，4 ，  4 4B ， ， 设直线 AB 的解析式为 y kx b  ， 则 1 4 4 4 k b k b       解得 3 4 1 k b     ∴直线 AB 的解析式为 3 14y x  ， 当 0x  时, 1y   01F ， ， 方法二:求 A B、 两点坐标同方法一,如图 2,作 FG BD , AH BD ,垂足分别为G 、H ,交 y 轴于点 N , 则四边形 FOMG 和四边形 NOMH 均为矩形,设 FO x ··········3 分 E DC AF B xO y l （图 2） G H M BGF BHA△ ∽△ BG FG BH AH   4 4 1 54 4 x   ， 解得 1x   0F ，1 ， (2)证明：方法一：在 Rt CEF△ 中， 1, 2CE EF  2 2 2 2 21 2 5CF CE EF      5CF  ， 在 Rt DEF△ 中， 4 2DE EF ， 2 2 2 2 24 2 20DF DE EF      2 5DF  由（1）得    1 1 4 1C D  ， ， ， 5CD  2 25 25CD   2 2 2CF DF CD   ， 90CFD  °  CF DF⊥ ， 方法二：由 （1）知 23 5 51 4 4 4AF AC       ， AF AC  ， 同理： BF BD ACF AFC   AC EF ∥ ACF CFO   AFC CFO   ， 同理： BFD OFD   90CFD OFC OFD      ° 即CF DF⊥ ， （3）存在. 解：如图 3，作 PM x⊥ 轴，垂足为点 M ··········9 分 E DC O F x y 图 3 M P l Q 又 PQ OP ⊥ Rt RtOPM OQP △ ∽ △ PM OM PQ OP   PQ PM OP OM   ， 设  21 04P x x x     ， ，则 21 4PM x OM x ， ①当 Rt RtQPO CFD△ ∽ △ 时， 5 1 22 5 PQ CF OP DF    ， 21 14 2 xPM OM x    解得 2x   1 21P ， ， ②当 Rt RtOPQ CFD△ ∽ △ 时， 2 5 2 5 PQ DF OP CF    ， 21 4 2 xPM OM x    解得 8x   2 816P ， 综上，存在点  1 21P ， 、  2 816P ， 使得 OPQ△ 与 CDF△ 相似. 70、(2009 宁夏)如图，抛物线 21 2 22 2y x x    与 x 轴交于 A B、 两点，与 y 轴交于C 点． （1）求 A B C、 、 三点的坐标； （2）证明 ABC△ 为直角三角形； （3）在抛物线上除C 点外，是否还存在另外一个点 P ，使 ABP△ 是直角三角形，若存在，请求出点 P 的 坐标，若不存在，请说明理由． 【关键词】二次函数的图象 【答案】解：（1）抛物线 21 2 22 2y x x    与 x 轴交于 A B、 两点， 21 2 2 02 2x x    ． 即 2 2 4 0x x   ． 解之得： 1 22 2 2x x  ， ． 点 A B、 的坐标为 ( 2 0) 2 2 0A B ，、（ ，）． 将 0x  代入 21 2 22 2y x x    ，得C 点的坐标为（0，2） （2） 6 2 3 3 2AC BC AB   ， ， ， 2 2 2AB AC BC   ， 则 90ACB  °， ABC△ 是直角三角形． （3）将 2y  代入 21 2 22 2y x x    得 21 2 2 22 2x x    ， 1 20 2x x  ， ． P 点坐标为 ( 2 2)， ． 71、（2009 肇庆）已知一元二次方程 2 1 0x px q    的一根为 2． y xBOA C （1）求 q 关于 p 的关系式； （2）求证：抛物线 2 y x px q   与 x 轴有两个交点； （3）设抛物线 2y x px q   的顶点为 M，且与 x 轴相交于 A（ 1x ，0）、B（ 2x ，0）两点，求使△AMB 面积最小时的抛物线的解析式． 【关键词】二次函数 【答案】（1）解：由题意，得 22 2 1 0p q    ，即 (2 5)q p   ． （2）证明：∵一元二次方程 2 0x px q   的判别式 2 4p q   ， 由（1）得 2 2 24(2 5) 8 20 ( 4) 4 0p p p p p           ，∴一元二次方程 2 0x px q   有两个 不相等的实根． ∴抛物线 2y x px q   与 x 轴有两个交点．（3）解：抛物线顶点的坐标为 24 2 4 p q pM     ， ，∵ 1 2x x， 是方程 2 0x px q   的两个根，∴ 1 2 1 2 . x x p x x q      ， ∴ 2 2 1 2 1 2 1 2| | | | ( ) 4 4AB x x x x x x p q       ∴ 2 2 21 4 1| | ( 4 ) 42 4 8AMB q pS AB p q p q   △ ，要使 AMBS△ 最小，只须使 2 4p q 最小．而由（2） 得 2 24 ( 4) 4p q p    ， 所以当 4p   时，有最小值 4，此时 AMBS△ 1 3q ， ． 故抛物线的解析式为 2 4 3y x x   ． 72、1．（2009 年中山）正方形 ABCD 边长为 4， M 、 N 分别 是 BC 、 CD 上的两个动点，当 M 点在 BC 上运动时，保持 AM 和 MN 垂直， （1）证明： Rt RtABM MCN△ ∽ △ ； （2）设 BM x ，梯形 ABCN 的面积为 y ，求 y 与 x 之间的 函 数 关 系 式；当 M 点运动到什么位置时，四边形 ABCN 面积最大，并 求 出 最 大 面积； （3）当 M 点运动到什么位置时 Rt RtABM AMN△ ∽ △ ，求 x 的值． 【关键词】与二次函数有关的面积问题，二次函数的极值问题 【 答 案 】 （ 1 ） 在 正 方 形 ABCD 中 ， 4 90AB BC CD B C      ， °， AM MN ， 90AMN  °， 90CMN AMB    °． 在 Rt ABM△ 中， 90MAB AMB    °， CMN MAB   ， Rt RtABM MCN △ ∽ △ ． （2） Rt RtABM MCN △ ∽ △ ， 4 4 AB BM x MC CN x CN     ， ， 2 4 4 x xCN    ， 2 2 21 4 1 14 4 2 8 ( 2) 102 4 2 2ABCN x xy S x x x                梯形 ， 当 2x  时， y 取最大值，最大值为 10． （3） 90B AMN    °， 要使 ABM AMN△ ∽△ ，必须有 AM AB MN BM  ， 由（1）知 AM AB MN MC  ， BM MC  ， 当点 M 运动到 BC 的中点时， ABM AMN△ ∽△ ，此时 2x  ． 2．（2009 年漳州）阅读材料，解答问题． 例：用图象法解一元二次不等式： 2 2 3 0x x   ． 解：设 2 2 3y x x   ，则 y 是 x 的二次函数． 1 0a   ， ∴抛物线开口向上． 又当 0y  时， 2 2 3 0x x   ， 解得 1 21 3x x  ， ． 由此得抛物线 2 2 3y x x   的大致图象如图所示． 观察函数图象可知：当 1x   或 3x  时， 0y  ．  2 2 3 0x x   的解集是： 1x   或 3x  ． （1）观察图象，直接写出一元二次不等式： 2 2 3 0x x   的解集是____________； （2）仿照上例，用图象法解一元二次不等式： 2 1 0x   ．（大致图象画在答题卡．．．上） 【关键词】二次函数与一元二次不等式的解集 【答案】（1） 1 3x   ． （2）解：设 2 1y x  ，则 y 是 x 的二次函数． 1 0a    ， 抛物线开口向上． 又当 0y  时， 2 1 0x   ，解得 1 21 1x x  ， ． 由此得抛物线 2 1y x  的大致图象如图所示． 观察函数图象可知：当 1x   或 1x  时， 0y  ． 2 1 0x   的解集是： 1x   或 1x  ． 75、（2009 年漳州）如图 1，已知：抛物线 21 2y x bx c   与 x 轴交于 A B、 两点，与 y 轴交于点C ，经 过 B C、 两点的直线是 1 22y x  ，连结 AC ． （1）B C、 两点坐标分别为 B（_____，_____）、C（_____，_____），抛物线的函数关系式为______________； （2）判断 ABC△ 的形状，并说明理由； （3）若 ABC△ 内部能否截出面积最大的矩形 DEFC （顶点 D E F、 、 、G 在 ABC△ 各边上）？若能， 求出在 AB 边上的矩形顶点的坐标；若不能，请说明理由． [抛物线 2y ax bx c   的顶点坐标是 24,2 4 b ac b a a     ] 1 1 1 1 2 1y x  x y C A O B x y C A O B x y 图 1 图 2(备用) 【关键词】二次函数与一元二次方程根之间的内在联系，待定系数法，与二次函数有关的面积问题，二次 函数的极值问题 【答案】（1） B （4，0）， (0 2)C ， ． 21 3 22 2y x x   ． （2） ABC△ 是直角三角形． 证明：令 0y  ，则 21 3 2 02 2x x   ． 1 21 4x x   ， ． ( 1 0)A  ， ． 解法一： 5 5 2 5AB AC BC   ， ， ． 2 2 25 20 25AC BC AB      ． ABC△ 是直角三角形． 解法二： 11 2 4 2 CO AOAO CO BO BO OC       ， ， ， 90AOC COB    °， AOC COB△ ∽△ ． ACO CBO   ． 90CBO BCO    °， 90ACO BCO    °．即 90ACB  °． ABC△ 是直角三角形． （3）能． ① 当矩形两个顶点在 AB 上时，如图 1，CO 交GF 于 H ． GF AB ∥ ， CGF CAB△ ∽△ ． GF CH AB CO   ． 解法一：设GF x ，则 DE x ， 2 5CH x ， 22 5DG OH OC CH x     ． 22 22 25 5DEFGS x x x x        矩形 · = 22 5 5 5 2 2x      ． 当 5 2x  时， S 最大． 5 12DE DG  ， ． ADG AOC△ ∽△ ， 1 1 22 2 AD DG AD OD OEAO OC       ， ， ， ． G A O B x y 图 1 D E FHC 1 02D     ， ， (2 0)E ， ． 解法二：设 DG x ，则 10 5 2 xDE GF   ． 2 210 5 5 5 55 ( 1)2 2 2 2DEFG xS x x x x        矩形 · ． 当 1x  时， S 最大． 51 2DG DE  ， ． ADG AOC△ ∽△ ， 1 1 22 2 AD DG AD OD OEAO OC       ， ， ， ． 1 02D     ， ， (2 0)E ， ． ② 当矩形一个顶点在 AB 上时， F 与C 重合，如图 2， DG BC ∥ ， AGD ACB△ ∽△ ． GD AG BC AF   ． 解法一：设GD x ， 5, 2 5AC BC   ， 5 2 xGF AC AG     ．  215 52 2DEFG xS x x x       矩形 · =  21 552 2x   ． 当 5x  时， S 最大． 55 2GD AG  ， ， 2 2 5 2AD AG GD    ． 3 2OD  3 02D     ， 解法二：设 DE x ， 5AC  ， 2 5BC  ， GC x  ， 5AG x  ． 2 5 2GD x   ．   22 5 2 2 2 5DEFGS x x x x     矩形 · = 2 5 52 2 2x        当 5 2x  时， S 最大， 55 2GD AG  ， ． 2 2 5 2AD AG GD    ． 3.2OD  C A O B x y 图 2 D G G 0 x y A B C  3 02D     ， 综上所述：当矩形两个顶点在 AB 上时，坐标分别为 1 02     ， ，（2，0）；当矩形一个顶点在 AB 上时， 坐标为 3 02      ， 76、（2009 年哈尔滨）张大爷要围成一个矩形花圃．花圃的一 边利用足够 长的墙另三边用总长为 32 米的篱笆恰好围成．围成的花圃是 如图所示的 矩形 ABCD．设 AB 边的长为 x 米．矩形 ABCD 的面积为 S 平方米． （1）求 S 与 x 之间的函数关系式（不要求写出自变量 x 的 取值范围）． （2）当 x 为何值时，S 有最大值？并求出最大值． （参考公式：二次函数 2y ax bx c   （ 0a  ），当 2 bx a   时 ， 24 4 ac by a 最大(小)值 ) 【关键词】与二次函数有关的面积问题，二次函数的极值问题 【答案】（1）中，根据矩形的面积=长×宽，然后后用 x 表示出宽，再利用此公式即可.（2）此题给我们公 式了，所以降低了此题的难度，直接利用公式代入即可. 由题意得 (32 2 )S AB BC x x   22 32S x x    2 0a    ， S 有最大值． 32 82 2 ( 2) bx a        ． 2 24 32 1284 4 ( 2) ac bS a     最大值 8x  时， S 有最大值是 128． 77 、（ 2009 年 牡 丹 江 ） 如 图 二 次 函 数 2y x bx c   的 图 象 经 过  1A  ，0 和  3 0B ， 两点，且交 y 轴于点C ． （1）试确定b 、 c 的值； （2）过点C 作 CD x∥ 轴交抛物线于点 D，点 M 为此抛物线的顶 点 ， 试 确 定 MCD△ 的形状． 参考公式：顶点坐标 24 2 4 b ac b a a     ， 【关键词】抛物线的顶点，待定系数法 【答案】（1）将 A 、 B 两点坐标代入解析式，有： 0 1 0 9 3 b c b c        解得： 2 3b c   ， （2）求出抛物线的顶点  1 4M ，    0 3 2 3 2C D CD  ， ， ， ， CDM△ 是等腰直角三角形 78、5、（2009 年兰州）如图 17，某公路隧道横截面为抛 物线，其 最大高度为 6 米，底部宽度 OM 为 12 米. 现以 O 点为原点， OM 所 在 直线为 x 轴建立直角坐标系. (1)直接写出点 M 及抛物线顶点 P 的坐标； (2)求这条抛物线的解析式； (3)若要搭建一个矩形“支撑架”AD- DC- CB， 使 C、D 点在抛物线上，A、B 点在地面 OM 上， 则这个“支撑架”总长的最大值是多少？ 【关键词】二次函数的图像和性质以及应用 【答案】解：(1) M(12，0)，P(6，6). (2) 设抛物线解析式为： 6)6( 2  xay . ∵抛物线 6)6( 2  xay 经过点(0，0)， ∴ 6)60(0 2  a ，即 6 1a ∴抛物线解析式为： xxyxy 26 1,6)6(6 1 22  即 . (3) 设 A(m， 0)， 则 B(12-m ， 0) ， )26 1,12( 2 mmmC  ， )26 1,( 2 mmmD  . ∴“支撑架”总长 AD+DC+CB = )26 1()212()26 1( 22 mmmmm  = 15)3(3 11223 1 22  mmm . ∵ 此二次函数的图象开口向下.∴ 当 m = 3 米时，AD+DC+CB 有最大值为 15 米. 7、（2009 年遂宁）25.如图，二次函数的图象经过点 D(0， 39 7 )，且顶点 C 的横坐标为 4，该图象在 x 轴 上截得的线段 AB 的长为 6. ⑴求二次函数的解析式； ⑵在该抛物线的对称轴上找一点 P，使 PA+PD 最小，求出点 P 的坐标； ⑶在抛物线上是否存在点 Q，使△QAB 与△ABC 相似？如果存在，求出点 Q 的坐标；如果不存在，请说 明理由． 【关键词】二次函数的图像的解析式、图像与性质、相似 【答案】⑴设二次函数的解析式为：y=a(x-h)2+k，∵顶点 C 的横坐标为 4，且过点(0， 39 7 ) ∴y=a(x-4)2+k ka 1639 7 ………………①，又∵对称轴为直线 x=4，图象在 x 轴上截得的线 段长为 6，∴A(1，0)，B(7，0)，∴0=9a+k ………………②，由①②解得 a= 9 3 ，k= 3－ ，∴二次函数 的解析式为：y= 9 3 (x-4)2－ 3 ⑵∵点 A、B 关于直线 x=4 对称，∴PA=PB，∴PA+PD=PB+PD≥DB，∴当点 P 在线段 DB 上时 PA+PD 取得最小 值，∴DB 与对称轴的交点即为所求点 P，设直线 x=4 与 x 轴交于点 M，∵PM∥OD，∴∠BPM=∠BDO，又∠PBM= ∠DBO，∴△BPM∽△BDO，∴ BO BM DO PM  ∴ 3 3 7 339 7   PM ，∴点 P 的坐标为(4， 3 3 ) ⑶由⑴知点 C(4， 3 )，又∵AM=3，∴在 Rt△AMC 中，cot∠ACM= 3 3 ，∴∠ACM=60o，∵AC=BC，∴∠ACB=120o ①当点 Q 在 x 轴上方时，过 Q 作 QN⊥x 轴于 N，如果 AB=BQ，由△ABC∽△ABQ 有 BQ=6，∠ABQ=120o，则∠ QBN=60o，∴QN=3 3 ，BN=3，ON=10，此时点 Q(10， 33 )，如果 AB=AQ，由对称性知 Q(-2， 33 ) ②当点 Q 在 x 轴下方时，△QAB 就是△ACB，此时点 Q 的坐标是(4， 3 )，经检验，点(10， 33 )与(-2， 33 )都在抛物线上，综上所述，存在这样的点 Q，使△QAB∽△ABC，点 Q 的坐标为(10， 33 )或(-2， 33 ) 或(4， 3 )． 8、（2009 年济南）已知：抛物线的对称轴为与 x 轴交于 A B， 两点，与 y 轴交于点 C，其中  3 0A  ， 、  0 2C ， ． （1）求这条抛物线的函数表达式． （2）已知在对称轴上存在一点 P，使得 PBC△ 的周长最小．请求出点 P 的坐标． （3）若点 D 是线段OC 上的一个动点（不与点 O、点 C 重合）．过点 D 作 DE PC∥ 交 x 轴于点 E．连接 PD 、 PE ．设CD 的长为 m ， PDE△ 的面积为 S ．求 S 与 m 之间的函数关系式．试说明 S 是否存在最大值， 若存在，请求出最大值；若不存在，请说明理由． 【关键词】二次函数的图像和性质 A C x y BO  2 0y ax bx c a    1x   ， 【答案】解：（1）由题意得 12 9 3 0 2 b a a b c c           ，解得 2 3 4 3 2 a b c         ∴此抛物线的解析式为 22 4 23 3y x x   ， （2）连结 AC 、 BC .因为 BC 的长度一定，所以 PBC△ 周长最小，就是使 PC PB 最小. B 点关于对 称轴的对称点是 A 点， AC 与对称轴 1x   的交点即为所求的点 P . 设直线 AC 的表达式为 y kx b  ，则 3 0 2 k b b       ， ，解得 2 3 2 k b       ∴此直线的表达式为 2 23y x   ．把 1x   代入得 4 3y   ∴ P 点的坐标为 41 3      ， ， （ 3 ） S 存 在 最 大 值 ， 理 由 ： ∵ DE PC∥ ，即 DE AC∥ ．∴ OED OAC△ ∽△ ．∴ OD OE OC OA  ，即 2 2 3 m OE  ．∴ 3 33 32 2OE m AE OE m   ， ， 方法一：连结 OP OED POE POD OEDPDOES S S S S S    △ △ △ △四边形 =    1 3 4 1 1 33 2 1 3 22 2 3 2 2 2m m m m                     = 23 3 4 2m m  ，∵ 3 04   ∴当 1m  时， 3 3 3 4 2 4S    最大 ， 方法二： OAC OED AEP PCDS S S S S   △ △ △ △ =  1 1 3 1 3 4 13 2 3 2 12 2 2 2 2 3 2m m m m                =  223 3 3 314 2 4 4m m m      ， ∵ 3 04   ，∴当 1m  时， 3 4S 最大 。 9、（2009 年凉山州）如图，已知抛物线 2y x bx c   经过 (1 0)A ， ， (0 2)B ， 两点，顶点为 D ． （1）求抛物线的解析式； （2）将 OAB△ 绕点 A 顺时针旋转 90°后，点 B 落到点C 的位置，将抛物线沿 y 轴平移后经过点C ，求 平移后所得图象的函数关系式； （3）设（2）中平移后，所得抛物线与 y 轴的交点为 1B ，顶点为 1D ，若点 N 在平移后的抛物线上，且满 足 1NBB△ 的面积是 1NDD△ 面积的 2 倍，求点 N 的坐标． OA C x y B E P D y x B AO D （第 26 题） 【关键词】二次函数的图像的解析式、图像与性质 【答案】（1）已知抛物线 2y x bx c   经过 (1 0) (0 2)A B，， ， ， 0 1 2 0 0 b c c       解得 3 2 b c     ,所求抛物线的解析式为 2 3 2y x x   ． （2） (1 0)A ， ， (0 2)B ， ， 1 2OA OB  ， ,可得旋转后 C 点的坐标为 (31)， ,当 3x  时，由 2 3 2y x x   得 2y  ，可知抛物线 2 3 2y x x   过点 (3 2)， ,将原抛物线沿 y 轴向下平移 1 个单位后过点C ． 平移后的抛物线解析式为： 2 3 1y x x   ． （3）点 N 在 2 3 1y x x   上，可设 N 点坐标为 2 0 0 0( 3 1)x x x ， 将 2 3 1y x x   配方得 23 5 2 4y x      ，其对称轴为 3 2x  ． ①当 0 30 2x  时，如图①， 1 1 2NBB NDDS S △ △ 0 0 1 1 31 2 12 2 2x x           0 1x  此时 2 0 03 1 1x x    N 点的坐标为 (1 1)， ． ②当 0 3 2x  时，如图② 同理可得 0 0 1 1 31 22 2 2x x         0 3x  此时 2 0 03 1 1x x   点 N 的坐标为 (31)， ． 综上，点 N 的坐标为 (1 1)， 或 (31)， ． 83、3.（2009 年广州市）如图 13，二次函数 )0(2  pqpxxy 的图象与 x 轴交于 A、B 两点， 与 y 轴交于点 C（0，-1），ΔABC 的面积为 4 5 。 （1）求该二次函数的关系式； （2）过 y 轴上的一点 M（0，m）作 y 轴上午垂线，若该垂线与ΔABC 的 外接圆有公共点，求 m 的取值范围； （3）在该二次函数的图象上是否存在点 D，使四边形 ABCD 为直角梯形？ 若存在，求出点 D 的坐标；若不存在，请说明理由。 4.（2009 年衡阳市）已知二次函数的图象过坐标原点，它的顶点坐标是（1， －2），求这个二次函数的关系式． 【关键词】二次函数解析式的求法 【答案】解：设这个二次函数的关系式为 2)1( 2  xay 得： 2)10(0 2  a 解得： 2a y x C B A O N D B1 D1 图① y x C B A O D B1 D1 图② N ∴这个二次函数的关系式是 2)1(2 2  xy ，即 xxy 42 2  5.（2009 年益阳市）阅读材料： 如图 12-1，过△ABC 的三个顶点分别作出与水平线垂直的三条直 线，外侧两条直线之间的距离叫△ABC 的“水平宽”(a)，中间的这条 直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h)”.我们可得出 一种计算三角形面积的新方法： ahS ABC 2 1 ，即三角形面积等于水 平宽与铅垂高乘积的一半. 解答下列问题： 如图 12-2，抛物线顶点坐标为点 C(1,4),交 x 轴于点 A(3,0)，交 y 轴于点 B. (1)求抛物线和直线 AB 的解析式； (2)点 P 是抛物线(在第一象限内)上的一个动点，连结 PA，PB，当 P 点运动到顶点 C 时，求△CAB 的铅垂高 CD 及 CABS ； (3)是否存在一点 P，使 S△PAB= 8 9 S△CAB，若存在，求出 P 点的坐标；若不存在，请说明理由. 图 12-2 x C O y A B D 1 1 【关键词】二次函数 【答案】解：(1)设抛物线的解析式为： 4)1( 2 1  xay . 把 A（3,0）代入解析式求得 1a 所以 324)1( 22 1  xxxy . 设直线 AB 的解析式为： bkxy 2 由 322 1  xxy 求得 B 点的坐标为 )3,0( . 把 )0,3(A ， )3,0(B 代入 bkxy 2 中 解得： 3,1  bk 所以 32  xy . (2)因为 C 点坐标为(１,4) 所以当 x＝１时，y1＝4，y2＝2 所以 CD＝4-2＝2. 3232 1 CABS (平方单位). (3)假设存在符合条件的点 P，设 P 点的横坐标为 x，△PAB 的铅垂高为 h， 则 xxxxxyyh 3)3()32( 22 21  . 由 S△PAB= 8 9 S△CAB 得： 38 9)3(32 1 2  xx 化简得： 09124 2  xx B C 铅垂高 水平宽 h a 图 12-1 A 2 O 解得， 2 3x 将 2 3x 代入 322 1  xxy 中， 解得 P 点坐标为 )4 15,2 3( 89、（2009 年济宁市）某体育用品商店购进一批滑板，每件进价为 100 元，售价为 130 元，每星期可 卖出 80 件.商家决定降价促销，根据市场调查，每降价 5 元，每星期可多卖出 20 件. （1）求商家降价前每星期的销售利润为多少元？ （2）降价后，商家要使每星期的销售利润最大，应将售价定为多少元？最大销售利润是多少？ 【关键词】二次函数的实际应用 【答案】解：(1) （130-100）×80=2400（元）； （2）设应将售价定为 x 元，则销售利润 130( 100)(80 20)5 xy x     24 1000 60000x x    24( 125) 2500x    . 当 125x  时， y 有最大值 2500. ∴应将售价定为 125 元,最大销售利润是 2500 元. 90、2. （2009 年株洲市）（本题满分 10 分）如图 1， Rt ABC 中， 90A   ， 3tan 4B  ，点 P 在线段 AB 上运动，点Q 、R 分别在线段 BC 、AC 上，且使得四边形 APQR 是矩形．设 AP 的长为 x ，矩形 APQR 的面积为 y ，已知 y 是 x 的函数，其图象是过点（12，36）的抛物线的一部分（如图 2 所示）． （1）求 AB 的长； （2）当 AP 为何值时，矩形 APQR 的面积最大，并求出最大值． 为了解决这个问题，孔明和研究性学习小组的同学作了如下讨论： 张明：图 2 中的抛物线过点（12，36）在图 1 中表示什么呢？ 李明：因为抛物线上的点 ( , )x y 是表示图 1 中 AP 的长与矩形 APQR 面积的对应关系，那么，（12，36） 表示当 12AP  时， AP 的长与矩形 APQR 面积的对应关系. 赵明：对，我知道纵坐标 36 是什么意思了！ 孔明：哦，这样就可以算出 AB ，这个问题就可以解决了. 请根据上述对话，帮他们解答这个问题. R Q P C B A 图 1 图 2 【关键词】二次函数最值 【答案】（1）当 12AP  时， 36AP PQ  ∴ 3PQ  ， 又在 Rt BPQ 中， 3tan 4B  ，∴ 3 4 PQ PB  ∴ 4PB  ∴ 16AB  ……………4 分 （ 2 ） 解 法 一 ： 若 AP x ， 则 16PB x  ， 3 (16 )4PQ x  ， ∴ 3 (16 )4y x x  ， 整 理 得 23 ( 8) 484y x    ∴ 当 8x  时， 48y最大值＝ . 解法二：由 16AB  ，结合图象可知抛物线经过点（0，0）、（16，0）、（12，36），可设抛物线解析式为 ( 16)y ax x  ，将（12，36）代入求得 3 4a   ，∴ 3 ( 16)4y x x   ，整理得 23 ( 8) 484y x    ， ∴ 当 8x  时， 48y最大值＝ . 解法三：由 16AB  ，结合图象可知抛物线经过点（0，0）、（16，0），知抛物线对称轴为 8x  ，∴抛物 线顶点的横坐标为 8.∴当 8AP  时，矩形 APQR 的面积最大，此时， 8PB  ，∴ 38 64PQ    ，∴最 大面积为 48. 3.（2009 年株洲市）已知 ABC 为直角三角形， 90ACB   ， AC BC ,点 A 、C 在 x 轴上，点 B 坐 标为（3 ， m ）（ 0m  ），线段 AB 与 y 轴相交于点 D ，以 P （1，0）为顶点的抛物线过点 B 、 D ． （1）求点 A 的坐标（用 m 表示）； （2）求抛物线的解析式； （3）设点Q 为抛物线上点 P 至点 B 之间的一动点，连结 PQ 并延长交 BC 于点 E ，连结 BQ 并延长交 AC 于点 F ，试证明： ( )FC AC EC 为定值． 【关键词】二次函数的综合题 【答案】（1）由 (3, )B m 可知 3OC  ， BC m ，又△ABC 为等腰直角三角形，∴ AC BC m  ， 3OA m  ，所以点 A 的坐标是（ 3 ,0m ）. ………………… 3 分 （2）∵ 45ODA OAD     ∴ 3OD OA m   ，则点 D 的坐标是（ 0, 3m  ）. 又抛物线顶点为 (1,0)P ，且过点 B 、 D ，所以可设抛物线的解析式为： 2( 1)y a x  ，得： 2 2 (3 1) (0 1) 3 a m a m       解得 1 4 a m    ∴抛物线的解析式为 2 2 1y x x   ………7 分 （3）过点Q 作 QM AC 于点 M ，过点 Q 作 QN BC 于点 N ，设点 Q 的坐标是 2( , 2 1)x x x  ，则 2( 1)QM CN x   ， 3MC QN x   . ∵ //QM CE ∴ PQM ∽ PEC ∴ QM PM EC PC  即 2( 1) 1 2 x x EC   ，得 2( 1)EC x  ∵ //QN FC ∴ BQN ∽ BFC ∴ QN BN FC BC  即 23 4 ( 1) 4 x x FC    ，得 4 1FC x   又∵ 4AC  ∴ 4 4 4( ) [4 2( 1)] (2 2) 2( 1) 81 1 1FC AC EC x x xx x x             即 ( )FC AC EC 为定值 8. 93. （2009 年重庆市江津区）某商场在销售旺季临近时 ，某品牌的童装销售价格呈上升趋势，假如这种 童装开始时的售价为每件 20 元，并且每周（7 天）涨价 2 元，从第 6 周开始，保持每件 30 元的稳定价格 销售，直到 11 周结束，该童装不再销售。 （1）请建立销售价格 y（元）与周次 x 之间的函数关系； （ 2 ） 若 该 品 牌 童 装 于 进 货 当 周 售 完 ， 且 这 种 童 装 每 件 进 价 z （ 元 ） 与 周 次 x 之 间 的 关 系 为 12)8(8 1 2  xz ， 1≤ x ≤11，且 x 为整数，那么该品牌童装在第几周售出后，每件获得利润最大？ 并求最大利润为多少？ 【关键词】二次函数极值 【答案】【答案】（1） 20 2( 1) 2 18 30 x xy       (1 6)( 11)( ) x x x x     为整数) (6 为整数 （2）设利润为 w 2 2 2 2 1 120 2( 1) ( 8) 12 14(1 6)8 8 1 130 ( 8) 12 ( 8) 18(6 11)8 8 ( y z x x x x xw y z x x x x                            为整数 为整数) 21 148w x  当 5x  时， 117 (8w 最大 元) 21 ( 8) 188w x   当 11x  时， 1 19 18 1 188 8w     最大 119 ( )8  元 综上知：在第 11 周进货并售出后，所获利润最大且为每件 119 8 元. 94、 （2009 年重庆市江津区）如图，抛物线 cbxxy  2 与 x 轴交与 A(1,0),B(- 3，0)两点， （1）求该抛物线的解析式； （2）设（1）中的抛物线交 y 轴与 C 点，在该抛物线的对称轴上是否存在点 Q，使得△QAC 的周长最小？ 若存在，求出 Q 点的坐标；若不存在，请说明理由. （3）在（1）中的抛物线上的第二象限上是否存在一点 P，使△PBC 的面积最大？，若存在，求出点 P 的 坐标及△PBC 的面积最大值.若没有，请说明理由. 【关键词】与二次函数有关的面积问题 【答案】解：（1）将 A（1，0）B（-3，0）代入 2y x bx c    中得 1 0 9 3 0 b c b c         ∴ 2 3 b c     ∴抛物线解析式为： 2 2 3y x x    （2）存在 理由如下：由题意知 A、B 两点关于抛物线的对称轴 1x   对称 ∴直线 BC 与 1x   的交点即为 Q 点，此时△AQC 周长最小 ∵ 2 2 3y x x    ∴C 的坐标为：（0，3） 直线 BC 解析式为 3y x  Q 点坐标即为 1 3 x y x      的解 ∴ 1 2 x y     ∴Q（-1，2） 第 26 题图 AB C （3）答：存在 理由如下： 设 P 点 2( , 2 3)x x x   ( 3 0)x   ∵ BPC BOCBPCOS S S  四边形 = 9 2BPCOS 四边形 若 BPCOS四边形 有最大值，则 BPCS 就最大， 过 P 点作 PE⊥ x 轴于 E ∴ Rt BPEBPCO PEOCS S S 四边形 直角梯形 1 1 ( )2 2BE PE OE PE OC    2 21 1( 3)( 2 3) ( )( 2 3 3)2 2x x x x x x           23 3 9 27( )2 2 2 8x     当 3 2x   时， BPCOS四边形 最大= 9 27 2 8  ∴ BPCS 最大= 9 27 9 27 2 8 2 8    当 3 2x   时， 2 152 3 4x x    ∴点 P 坐标为 3 15( , )2 4  . 95、3．(2009 年宁德市)（本题满分 13 分）如图，已知抛物线 C1：   52 2  xay 的顶点为 P，与 x 轴相交于 A、B 两点（点 A 在点 B 的左边），点 B 的横坐标是 1． （1）求P点坐标及a的值；（4分） （2）如图（1），抛物线 C2 与抛物线 C1 关于 x 轴对称，将抛物线 C2 向右平移，平移后的抛物线记为 C3，C3 的顶点为 M，当点 P、M 关于点 B 成中心对称时，求 C3 的解析式；（4 分） （3）如图（2），点 Q 是 x 轴正半轴上一点，将抛物线 C1 绕点 Q 旋转 180°后得到抛物线 C4．抛物 线 C4 的顶点为 N，与 x 轴相交于 E、F 两点（点 E 在点 F 的左边），当以点 P、N、F 为顶点的三角形是直 角三角形时，求点 Q 的坐标．（5 分） 【关键词】二次函数,勾股定理的运用 解：（1）由抛物线 C1：   52 2  xay 得 顶点 P 的为（-2，-5） ∵点 B（1，0）在抛物线 C1 上 ∴   5210 2  a 解得，a＝5 9 （2）连接 PM，作 PH⊥x 轴于 H，作 MG⊥x 轴于 G ∵点 P、M 关于点 B 成中心对称 ∴PM 过点 B，且 PB＝MB ∴△PBH≌△MBG ∴MG＝PH＝5，BG＝BH＝3 ∴顶点 M 的坐标为（4，5） 抛物线 C2 由 C1 关于 x 轴对称得到，抛物线 C3 由 C2 平移得到 ∴抛物线 C3 的表达式为   549 5 2  xy （3）∵抛物线 C4 由 C1 绕点 x 轴上的点 Q 旋转 180°得到 ∴顶点 N、P 关于点 Q 成中心对称 由（2）得点 N 的纵坐标为 5 设点 N 坐标为（m，5） 作 PH⊥x 轴于 H，作 NG⊥x 轴于 G 作 PK⊥NG 于 K ∵旋转中心 Q 在 x 轴上 ∴EF＝AB＝2BH＝6 ∴FG＝3，点 F 坐标为（m+3，0） H 坐标为（2，0），K 坐标为（m，-5）， 根据勾股定理得 PN2＝NK2+PK2＝m2+4m+104 PF2＝PH2+HF2＝m2+10m+50 NF2＝52+32＝34 ①当∠PNF＝90º时，PN2+ NF2＝PF2，解得 m＝44 3 ，∴Q 点坐标为（19 3 ，0） ②当∠PFN＝90º时，PF2+ NF2＝PN2，解得 m＝10 3 ，∴Q 点坐标为（2 3 ，0） ③∵PN＞NK＝10＞NF，∴∠NPF≠90º 综上所得，当 Q 点坐标为（19 3 ，0）或（2 3 ，0）时，以点 P、N、F 为顶点 的三角形是直角三角形． 4.(2009 年河北)已知抛物线 2y ax bx  经过点 ( 3 3)A  ， 和点 P （t，0），且 t ≠ 0． y x A O B P M 图 1 C1 C2 C3 图（1） y x A O B P N 图 2 C1 C4 Q E F 图（2） y x A O B P M 图(1) C1 C2 C3 H G y x A O B P N 图(2) C1 C4 Q E F H G K （1）若该抛物线的对称轴经过点 A，如图 12， 请通过观察图象，指出此时 y 的最小值， 并写出 t 的值； （2）若 4t   ，求 a、b 的值，并指出此时抛 物线的开口方向； （3）直．接．写出使该抛物线开口向下的 t 的一个值． 【关键词】二次函数 解：（1）－3． t =－6． （2）分别将（－4，0）和（－3，－3）代入 2y ax bx  ，得 0 16 4 , 3 9 3 . a b a b      解得 1, 4. a b    向上． （3）－1（答案不唯一）． 【注：写出 t＞－3 且 t≠0 或其中任意一个数均给分】 98、(2009 年潍坊)如图，在平面直角坐标系 xOy 中，半径为 1 的圆的圆心 O 在坐标原点，且与两坐标轴分 别交于 A B C D、 、 、 四点．抛物线 2y ax bx c   与 y 轴交于点 D ，与直线 y x 交于点 M N、 ，且 MA NC、 分别与圆O 相切于点 A 和点C ． （1）求抛物线的解析式； （2）抛物线的对称轴交 x 轴于点 E ，连结 DE ，并延长 DE 交圆O 于 F ，求 EF 的长． （3）过点 B 作圆O 的切线交 DC 的延长线于点 P ，判断点 P 是否在抛物线上，说明理由． 解：（1）圆心O 在坐标原点，圆O 的半径为 1， 点 A B C D、 、 、 的坐标分别为 ( 1 0) (0 1) (1 0) (01)A B C D ，、 ， 、 ，、 ， 抛物线与直线 y x 交于点 M N、 ，且 MA NC、 分别与圆O 相切于点 A 和点C ，  ( 1 1) (11)M N ， 、 ， ． 点 D M N、 、 在抛物线上，将 (01) ( 1 1) (11)D M N ，、 ， 、 ， 的坐标代入 2y ax bx c   ，得： 1 1 1 c a b c a b c          解之，得： 1 1 1 a b c       抛物线的解析式为： 2 1y x x    ． （2） 2 2 1 51 2 4y x x x           A OP x y 图 12 - 3 - 3 O x y N C D E F BM A 抛物线的对称轴为 1 2x  ， 1 1 512 4 2OE DE    ， ． 连结 90BF BFD ， °， BFD EOD△ ∽△ ， DE OD DB FD   ， 又 5 1 22DE OD DB  ， ， ， 4 5 5FD  ， 4 5 5 3 5 5 2 10EF FD DE      ． （3）点 P 在抛物线上． 设过 D C、 点的直线为： y kx b  ， 将点 (1 0) (01)C D，、 ， 的坐标代入 y kx b  ，得： 1 1k b  ， ， 直线 DC 为： 1y x   ． 过点 B 作圆 O 的切线 BP 与 x 轴平行， P 点的纵坐标为 1y   ， 将 1y   代入 1y x   ，得： 2x  ．  P 点的坐标为 (2 1)， ， 当 2x  时， 2 21 2 2 1 1y x x          ， 所以， P 点在抛物线 2 1y x x    上． 说明：解答题各小题中只给出了 1 种解法，其它解法只要步骤合理、解答正确均应得到相应的分数． 99、（09 湖北宜昌）已知：直角梯形 OABC 的四个顶点是 O(0，0)，A( 3 2 ，1)， B(s，t)，C( 7 2 ，0)，抛物 线 y=x2＋mx－m 的顶点 P 是直角梯形 OABC 内部或边上的一个动点，m 为常数． (1)求 s 与 t 的值，并在直角坐标系中画出．．直角梯形 OABC； (2)当抛物线 y=x2＋mx－m 与直角梯形 OABC 的边 AB 相交时，求 m 的取值范围． （第 24 题） 【关键词】二次函数 2y ax bx c   （a≠0）与 a，b，c 的关系、解一元一次不等式（组）、不等式（组） 的简单应用 【答案】解：（1）如图，在坐标系中标出 O，A，C 三点，连接 OA，OC． ∵∠AOC≠90°， ∴∠ABC=90°， 故 BC⊥OC， BC⊥AB，∴B（ 7 2 ，1）． 即 s= 7 2 ，t=1．直角梯形如图所画． （大致说清理由即可） O x y N C D E F BM A P A B C （2）由题意，y=x2+mx－m 与 y=1（线段 AB）相交， 得， 1 2y = x mx m, y = .     ∴1＝x2+mx－m， 由 (x－1)(x+1+m)=0，得 1 21, 1x x m    ． ∵ 1x =1< 3 2 ，不合题意，舍去． ∴抛物线 y=x2+mx-m 与 AB 边只能相交于（ 2x ，1）， ∴ 3 2 ≤－m－1≤ 7 2 ，∴ 9 2 5 2 m   ． ① 又∵顶点 P( 2 4 2 4 ,m m m  )是直角梯形 OABC 的内部和其边上的一个动点， ∴ 70 2 2 m   ，即 7 0m   ． ② ∵ 2 2 24 ( 2) 4 ( 1) 4 4 2 1 1m m m m          ， （或者抛物线 y=x2+mx－m 顶点的纵坐标最大值是 1） ∴点 P 一定在线段 AB 的下方． 又∵点 P 在 x 轴的上方， ∴ 2 4 4 0m m  ， ( 4) 0,m m   ∴ 0, 0, 4 0 4 0 m m m m           或者 ． 4 (9 ) 0. m  分 ③（9 分） 又∵点 P 在直线 y= 2 3 x 的下方，∴ 2 4 2 ( ) 4 3 2 m m m    ，（10 分）即 (3 8) 0.m m   0, 0, 3 8 0 3 8 0. m m m m           或者 8 0. 3 m m   (11分)，或 ④ 由①②③④ ，得 4  8 3 m   ． 100、（09 湖南怀化）如图 11，已知二次函数 22)( mkmxy  的图象与 x 轴相交于两个不同的点 1( 0)A x， 、 2( 0)B x ， ，与 y 轴的交点为C ．设 ABC△ 的外接圆的圆心为点 P ． （1）求 P⊙ 与 y 轴的另一个交点 D 的坐标； （2）如果 AB 恰好为 P⊙ 的直径，且 ABC△ 的面积等于 5 ， 求 m 和 k 的 值． 【关键词】二次函数的应用、与二次函数有关的面积问题 【答案】解 （1）易求得点C 的坐标为 (0 )k， 由 题 设 可 知 1 2x x， 是 方 程 0)( 22  mkmx 即 022  kmxx 的两根，所以 2 1 2 2 ( 2 ) 4 2 m m kx    ， ， 所 1 2 1 22x x m x x k    ， 如图 3，∵⊙P 与 y 轴的另一个交点为 D，由于 AB、CD 是⊙P 的两条相交弦， 设 它 们 的 交 点 为 点 O ， 连 结 DB ， ∴△AOC∽△DOC ， 则 .121  k k k xx OC OBOAOD 由题意知点C 在 y 轴的负半轴上，从而点 D 在 y 轴的正半轴上， 所以点 D 的坐标为（0，1） （2）因为 AB⊥CD， AB 又恰好为⊙P 的直径，则 C、D 关于点 O 对 称，所以点 C 的坐标为 (0 1)， ，即 1k ）又 2 2 2 2 2 1 2 1 1 2( ) 4 ( 2 ) 4 2 2 1AB x x x x x x m k m k m            ， 所以 21 1 2 1 1 52 2ABCS AB OC m      △ 解得 .2m 101、（09 湖南邵阳）如图（十二），直线l 的解析式为 4y x   ，它与 x 轴、y 轴分别相交于 A B、 两点．平 行于直线l 的直线 m 从原点 O 出发，沿 x 轴的正方形以每秒 1 个单位长度的速度运动，它与 x 轴、 y 轴分 别相交于 M N、 两点，设运动时间为t 秒（ 0 4t ≤ ）． （1）求 A B、 两点的坐标； （2）用含t 的代数式表示 MON△ 的面积 1S ； （ 3 ） 以 MN 为 对 角 线 作 矩 形 OMPN ，记 MPN△ 和 OAB△ 重合 部 分 的面积为 2S ， ①当 2 t ≤ 4 时，试探究 2S 与t 之间 的 函 数关系式； ②在直线 m 的运动过程中，当 t 为何 值时， 2S 为 OAB△ 面积的 5 16 ？ 【关键词】直角坐标系、一元二次方程解法及应用、一次函数的实际应用、二次函数的应用、与二次函数 有关的面积问题 【答案】解 （1）当 0x  时， 4y  ；当 0y  时， 4x  ． (4 0) 0 4A B ，，（ ，）； （2） 1OM OAMN AB ON OB    ∥ ， ， 2 1 1 1 2 2OM ON t S OM ON t     ， · ； （3）①当 2 4t ≤ 时，易知点 P 在 OAB△ 的外面，则点 P 的坐标为 ( )t t， , F 点的坐标满足 4 x t y t      ， ，即 ( 4 )F t t， ， 同理 (4 )E t t ， ，则 2 4PF PE t t t    (4- ) ， 所以 2 MPN PEF OMN PEFS S S S S   △ △ △ △ 2 2 21 1 1 1 32 4 2 4 8 82 2 2 2 2t PE PF t t t t t         · ( )( ) ； ②当 0 2t ≤ 时， 2 2 2 1 1 5 1 54 42 2 16 2 2S t t     ， ， 解得 1 25 0 5 2t t    ， ，两个都不合题意，舍去； 当 2 4t ≤ 时， 2 2 3 58 82 2S t t     ，解得 3 4 73 3t t ， ， 综上得，当 7 3t  或 3t  时， 2S 为 OAB△ 的面积的 5 16 ． 102、（2009 安徽年）23．已知某种水果的批发单价与批发量的函数关系如图（1）所示． （1）请说明图中①、②两段函数图象的实际意义． O M A PN yl m x B O M A PN yl m x B E P F 图十二 【解】 （2）写出批发该种水果的资金金额 w（元）与批发量 m（kg）之间的 函数关系式；在下图的坐标系中画出该函数图象；指出金额在什 么范围内，以同样的资金可以批发到较多数量的该种水果． 【解】 （3）经调查，某经销商销售该种水果的日最高销量与零售价之间的函 数关系如图（2）所示，该经销商拟每日售出 60kg 以上该种水果， 且当日零售价不变，请你帮助该经销商设计进货和销售的方案， 使得当日获得的利润最大． 【解】 【关键词】二次函数综合 【答案】（1）解：图①表示批发量不少于 20kg 且不多于 60kg 的该种水果， 可按 5 元/kg 批发；……3 分 图②表示批发量高于 60kg 的该种水果，可按 4 元/kg 批发 （2）解：由题意得： 20 60 60 5 4 m m w m m    ≤ ≤（ ） ）＞（ ，函数图象如图所示． 由图可知资金金额满足 240＜w≤300 时，以同样的资金可 批发到较多数量的该种水果． （3）解法一： 设当日零售价为 x 元，由图可得日最高销量 320 40w m  当 m＞60 时，x＜6.5 由题意，销售利润为 2( 4)(320 40 ) 40[ ( 6) 4]y x m x       当 x＝6 时， 160y 最大值 ，此时 m＝80 即经销商应批发 80kg 该种水果，日零售价定为 6 元/kg， 当日可获得最大利润 160 元． 解法二： 设日最高销售量为 xkg（x＞60） 则由图②日零售价 p 满足： 320 40x p  ，于是 320 40 xp  销售利润 2320 1( 4) ( 80) 16040 40 xy x x      当 x＝80 时， 160y 最大值 ，此时 p＝6 即经销商应批发 80kg 该种水果，日零售价定为 6 元/kg， 当日可获得最大利润 160 元． （2009 年湖北荆州）23．（7 分）已知：点 P（ 1a  ， 1a  ）关于 x 轴的对称点在反比例函数 8 ( 0)y xx    的图像上， y 关于 x 的函数 2 2 (2 1) 1y k x k x    的图像与坐标轴只有两个不同的交点 A﹑B，求 P 点坐标和△PAB 的面积. 【关键词】二次函数和反比例函数相关 【答案】 （2009 年湖北荆州）24．（10 分）由于国家重点扶持节能环保产业，某种节能产品的销售市场逐渐回暖．某 经销商销售这种产品，年初与生产厂家签订了一份进货合同，约定一年内进价为 0.1 万元／台，并预付了 5 万元押金。他计划一年内要达到一定的销售量，且完成此销售量所用的进货总金额加上押金控制在不低 于 34 万元，但不高于 40 万元．若一年内该产品的售价 y （万元／台）与月次 x （1 12x  且为整数） 满足关系是式： 0.05 0.25 (1 4) 0.1 (4 6) 0.015 0.01 (6 12) x x y x x x             ，一年后发现实际．．每月的销售量 p （台）与月次 x 之间 存在如图所示的变化趋势． ⑴ 直接写出实际．．．．．．每月的销售量 p （台）与月次 x 之间 的函数关系式； ⑵ 求前三个月中每月的实际销售利润 w （万元）与月 次 x 之间的函数关系式； ⑶ 试判断全年哪一个月的的售价最高，并指出最高售价； ⑷ 请通过计算说明他这一年是否完成了年初计划的销售量． 36 4 月 20 40 Ｏ x p （台） 12 月 【关键词】二次函数综合题 【答案】 （2009 年茂名市）10．如图，把抛物线 2y x 与直线 1y  围成的图形OABC 绕原点 O 顺时针旋转90°后， 再沿 x 轴向右平移 1 个单位得到图形 1 1 1 1O A B C ，则下列结论错误．．的是（ ） A．点 1O 的坐标是 (1 0)， B．点 1C 的坐标是 (2 1)， C．四边形 1 1 1O BA B 是矩形 D．若连接OC，则梯形 1 1OCA B 的面积是 3 O y x1O B 1B 1C 1A11A （ ，） 11C（，） 【关键词】二次函数与圆 【答案】 103、（2009 年茂名市）茂名石化乙烯厂某车间生产甲、乙两种塑料的相关信息如下表，请你解答下列问题： 出厂价 成本价 排污处理费 甲种塑料 2100（元/吨） 800（元/吨） 200（元/吨） 乙种塑料 2400（元/吨） 1100（元/吨） 100（元/吨） 每月还需支付设备管理、 维护费 20000 元 （1）设该车间每月生产甲、乙两种塑料各 x 吨，利润分别为 1y 元和 2y 元，分别求 1y 和 2y 与 x 的函 数关系式（注：利润=总收入-总支出）；（6 分） （2）已知该车间每月生产甲、乙两种塑料均不超过 400 吨，若某月要生产甲、乙两种塑料共 700 吨， 求该月生产甲、乙塑料各多少吨，获得的总利润最大？最大利润是多少？（4 分） 【关键词】二次函数综合运用 【答案】 104、（2009 年茂名市）如图，在 Rt ABC△ 中， 90 60 24BAC C BC    °， °， ，点 P 是 BC 边上的 动点（点 P 与点 B C、 不重合），过动点 P 作 PD BA∥ 交 AC 于点 D． （1）若 ABC△ 与 DAP△ 相似，则 APD 是多少度？ （2 分） （2）试问：当 PC 等于多少时， APD△ 的面积最大？最大面积是多少？ （4 分） （3）若以线段 AC 为直径的圆和以线段 BP 为直径的圆相外切，求线段 BP 的长．（4 分） 60° A D CB P 【关键词】二次函数、圆、相似综合题 【答案】 105、1．（2009 年湖北十堰市）如图①， 已知抛物线 32  bxaxy （a≠0）与 x 轴交于点 A(1，0)和点 B (－3，0)，与 y 轴交于点 C． 价 目品 种 (1) 求抛物线的解析式； (2) 设抛物线的对称轴与 x 轴交于点 M ，问在对称轴上是否存在点 P，使△CMP 为等腰三角形？若存在， 请直接写出所有符合条件的点 P 的坐标；若不存在，请说明理由． (3) 如图②，若点 E 为第二象限抛物线上一动点，连接 BE、CE，求四边形 BOCE 面积的最大值，并求此 时 E 点的坐标． 【关键词】二次函数和抛物线有关概念、二次函数的极值问题 【答案】解: (1)由题知:      0339 03 ba ba ， 解得:      2 1 b a ， ∴ 所求抛物线解析式为: 322  xxy 。 (2) 存在符合条件的点 P, 其坐标为 P (－1, 10 )或 P(－1,－ 10 ) 或 P (－1, 6) 或 P (－1, 3 5 )。 (3)解法①： 过点 E 作 EF⊥x 轴于点 F , 设 E ( a ,- 2a -2a＋3 )( －3< a < 0 ) ∴EF=- 2a -2a＋3，BF=a＋3，OF=－a， ∴S 四边形 BOCE = 2 1 BF·EF + 2 1 (OC +EF)·OF = 2 1 ( a＋3 )·(－ 2a －2a＋3) + 2 1 (－ 2a －2a＋6)·（－a） = 2 9 2 9 2 3 2  aa =－ 2 3 2)2 3( a + 8 63 ∴ 当 a =－ 2 3 时，S 四边形 BOCE 最大, 且最大值为 8 63 ．， 此时，点 E 坐标为 (－ 2 3 ， 4 15 )， 解法②： 过点 E 作 EF⊥x 轴于点 F， 设 E ( x , y ) ( －3< x < 0 ) ， 则 S 四边形 BOCE = 2 1 (3 + y )·(－x) + 2 1 ( 3 + x )·y = 2 3 ( y－x)= 2 3 ( 332 x－－x ) = － 2 3 2)2 3( x + 8 63 ∴ 当 x =－ 2 3 时，S 四边形 BOCE 最大，且最大值为 8 63 ． ， 此时，点 E 坐标为 (－ 2 3 ， 4 15 ) ， 说明:（1）抛物线解析式用其它形式表示，只要正确不扣分. （2）直接应用公式法求抛物线顶点坐标或最大值不扣分． （3）其它解法请参照评分说明给分. 107、（2009 年山东青岛市）某水产品养殖企业为指导该企 业某种水产品的养殖和销售，对历年市场行情和水产品养殖 情况进行了调查．调查发现这种水产品的每千克售价 1y （元）与销售月份 x （月）满足关系式 3 368y x   ，而 其每千克成本 2y （元）与销售月份 x （月）满足的函数关 系如图所示． （1）试确定 b c、 的值； （2）求出这种水产品每千克的利润 y （元）与销售月份 x （月）之间的函数关系式； （3）“五·一”之前，几月份出售这种水产品每千克的利润最大？最大利润是多少？ 【关键词】二次函数和抛物线有关概念、二次函数的极值问题 【答案】解：（1）由题意： 2 2 125 3 38 124 4 48 b c b c           解得 718 129 2 b c      （2） 1 2y y y  23 1 15 136 298 8 8 2x x x         21 3 168 2 2x x    ； （3） 21 3 168 2 2y x x    21 1 1( 12 36) 4 68 2 2x x      21 ( 6) 118 x    ∵ 1 08a    ， ∴抛物线开口向下． 在对称轴 6x  左侧 y 随 x 的增大而增大． 25 24 y2（元） x（月）1 2 3 4 5 6 7 8 9 10 11 12 第 2 题图 2 2 1 8y x bx c   O 由题意 5x  ，所以在 4 月份出售这种水产品每千克的利润最大． 最大利润 21 1(4 6) 11 108 2      （元）． 108、（2009 年新疆乌鲁木齐市）如图 9，在矩形OABC 中，已知 A 、C 两点的坐标分别为 (4 0) (0 2)A C，、 ， ， D 为OA 的中点．设点 P 是 AOC 平分线上的一个动点（不与点O 重合）． （1）试证明：无论点 P 运动到何处， PC 总与 PD 相等； （2）当点 P 运动到与点 B 的距离最小时，试确定过O P D、 、 三点的 抛物线的解析式； （3）设点 E 是（2）中所确定抛物线的顶点，当点 P 运动到何处时， PDE△ 的周长最小？求出此时点 P 的坐标和 PDE△ 的周长； （ 4 ） 设 点 N 是 矩 形 OABC 的 对 称 中 心 ， 是 否 存 在 点 P ， 使 90CPN  °？若存在，请直接写出点 P 的坐标． 【关键词】确定一次函数解析式、次函数 2y ax bx c   （a≠0）与 a，b，c 的关系 【答案】解：（1）∵点 D 是OA 的中点，∴ 2OD  ，∴OD OC ． 又∵OP 是 COD 的角平分线，∴ 45POC POD    °， ∴ POC POD△ ≌△ ，∴ PC PD ． （2）过点 B 作 AOC 的平分线的垂线，垂足为 P ，点 P 即为所求． 易知点 F 的坐标为（2，2），故 2BF  ，作 PM BF⊥ ， ∵ PBF△ 是等腰直角三角形，∴ 1 12PM BF  ， ∴点 P 的坐标为（3，3）． ∵抛物线经过原点， ∴设抛物线的解析式为 2y ax bx  ． 又∵抛物线经过点 (3 3)P ， 和点 (2 0)D ， ， ∴有 9 3 3 4 2 0 a b a b      解得 1 2 a b     ∴抛物线的解析式为 2 2y x x  ． （3）由等腰直角三角形的对称性知 D 点关于 AOC 的平分线的对称点即为C 点． 连接 EC ，它与 AOC 的平分线的交点即为所求的 P 点（因为 PE PD EC  ，而两点之间线段最短）， 此时 PED△ 的周长最小． ∵抛物线 2 2y x x  的顶点 E 的坐标 (1 1)， ，C 点的坐标 (0 2)， ， 设CE 所在直线的解析式为 y kx b  ，则有 1 2 k b b      ，解得 3 2 k b     ． ∴CE 所在直线的解析式为 3 2y x   ． 点 P 满足 3 2y x y x      ，解得 1 2 1 2 x y     ，故点 P 的坐标为 1 1 2 2      ， ． PED△ 的周长即是 10 2CE DE   ． （4）存在点 P ，使 90CPN  °．其坐标是 1 1 2 2      ， 或 (2 2)， ． 109、19．（2009 年佛山市）（1）请在坐标系中画出二次函数 2 2y x x   的大致图象； （2）在同一个坐标系中画出 2 2y x x   的图象向上平移两个单位后的图象； （3）直接写出平移后的图象的解析式. y O x P D B (4 0)A ， (0 2)C ， 图 9 y O xD B (4 0)A ， C P E (0 2)， F M 注：图中小正方形网格的边长为1. 【关键词】二次函数综合应用 【答案】（1）画图（略） 注：基本反映图形的特征（如顶点、对称性、变化趋势、平滑）给2分，满足其中的两至三项给1分，满足 一项以下给0分； （2）画图、写解析式（略） 注：画图满分2分，同（1）的标准；写解析式2分（无过程不扣分）． 110、（2009 年广东省）正方形 ABCD 边长为 4， M 、 N 分别是 BC 、CD 上的两个动点， 当 M 点 在 BC 上运动时，保持 AM 和 MN 垂直， （1）证明： Rt RtABM MCN△ ∽ △ ； （2）设 BM x ，梯形 ABCN 的面积为 y ，求 y 与 x 之间的函数关系式；当 M 点运动到什么位置时， 四边形 ABCN 面积最大，并求出最大面积； （3）当 M 点运动到什么位置时 Rt RtABM AMN△ ∽ △ ，求此时 x 的值． D M A B C N 【关键词】正方形的性质；相似三角形判定和性质；直角梯形；与二次函数有关的面积问题；二次函数的 极值问题；相似三角形有关的计算和证明 【答案】 解：（1）在正方形 ABCD 中， 4 90AB BC CD B C      ， °， AM MN ⊥ ， 90AMN  °， 90CMN AMB    °， 在 Rt ABM△ 中， 90MAB AMB    °， CMN MAB   ， Rt RtABM MCN △ ∽ △ ， （2） Rt RtABM MCN △ ∽ △ ， 4 4 AB BM x MC CN x CN     ， ， 2 4 4 x xCN    ，   2 221 4 1 14 4 2 8 2 102 4 2 2ABCN x xy S x x x               梯形 · ， 当 2x  时， y 取最大值，最大值为 10． （3） 90B AMN    °， 要使 ABM AMN△ ∽△ ，必须有 AM AB MN BM  ， 由（1）知 AM AB MN MC  ， x y O 第 19 题图 BM MC  ， 当点 M 运动到 BC 的中点时， ABM AMN△ ∽△ ，此时 2x  ． （其它正确的解法，参照评分建议按步给分） 2．（2009 年山西省）某批发市场批发甲、乙两种水果，根据以往经验和市场行情，预计夏季某一段时间内， 甲种水果的销售利润 y甲 （万元）与进货量 x （吨）近似满足函数关系 0.3y x甲 ；乙种水果的销售利 润 y乙 （万元）与进货量 x （吨）近似满足函数关系 2y ax bx 乙 （其中 0a a b ， ， 为常数），且进 货量 x 为 1 吨时，销售利润 y乙 为 1.4 万元；进货量 x 为 2 吨时，销售利润 y乙 为 2.6 万元． （1）求 y乙 （万元）与 x （吨）之间的函数关系式． （2）如果市场准备进甲、乙两种水果共 10 吨，设乙种水果的进货量为t 吨，请你写出这两种水果所获 得的销售利润之和W （万元）与 t （吨）之间的函数关系式．并求出这两种水果各进多少吨时获得 的销售利润之和最大，最大利润是多少？ 【关键词】待定系数法；二次函数的极值问题；二次函数的应用 【答案】解：（1）由题意，得： 1.4 4 2 2.6 a b a b      ， ．解得 0.1 1.5 a b     ， ． ∴ 20.1 1.5y x x  乙 ． （2）    20.3 10 0.1 1.5W y y t t t      乙甲 ． ∴ 20.1 1.2 3W t t    ．  20.1 6 6.6W t    ．∴ 6t  时，W 有最大值为 6.6. ∴10 6 4  （吨）. 答：甲、乙两种水果的进货量分别为 4 吨和 6 吨时，获得的销售利润之和最大，最大利润是 6.6 万元. 5．（2009 年黄石市）已知关于 x 的函数 2 1y ax x   （ a 为常数） （1）若函数的图象与 x 轴恰有一个交点，求 a 的值； （2）若函数的图象是抛物线，且顶点始终在 x 轴上方，求 a 的取值范围． 【关键词】抛物线顶点；二次函数 2y ax bx c   （a≠0）与 a，b，c 的关系；二次函数与一元二次方程 根之间的内在联系 【答案】解：（1）当 0a  时，函数为 1y x  ，它的图象显然与 x 轴 只有一个交点 ( 1 0) ， ． 当 0a  时，依题意得方程 2 1 0ax x   有两等实数根． 1 4 0a    ， 1 4a  ． 当 0a  或 1 4a  时函数图象与 x 轴恰有一个交点． （2）依题意有 4 1 04 a a   分类讨论解得 1 4a  或 0a  ． 当 1 4a  或 0a  时，抛物线顶点始终在 x 轴上方． 6．（2009 年黄石市）为了扩大内需，让惠于农民，丰富农民的业余生活，鼓励送彩电下乡，国家决定对购 买彩电的农户实行政府补贴．规定每购买一台彩电，政府补贴若干元，经调查某商场销售彩电台数 y（台） 与补贴款额 x （元）之间大致满足如图①所示的一次函数关系．随着补贴款额 x 的不断增大，销售量也不 断增加，但每台彩电的收益 Z （元）会相应降低且 Z 与 x 之间也大致满足如图②所示的一次函数关系． 1200 800 0 400 y(台) x(元) z(元) x(元) 200 160 2000 图① 图② （1）在政府未出台补贴措施前，该商场销售彩电的总收益额为多少元？ （2）在政府补贴政策实施后，分别求出该商场销售彩电台数 y 和每台家电的收益 Z 与政府补贴款额 x 之 间的函数关系式； （3）要使该商场销售彩电的总收益 w（元）最大，政府应将每台补贴款额 x 定为多少？并求出总收益 w 的 最大值． 【关键词】确定一次函数解析式；一次函数的实际问题；二次函数的应用；二次函数的极值问题 【答案】解：（1）该商场销售家电的总收益为800 200 160000  （元） （2）依题意可设 1 800y k x  ， 2 200Z k x  有 1400 800 1200k   ， 2200 200 160k   ， 解得 1 2 11 5k k  ， ． 所以 800y x  ， 1 2005Z x   ． （3） 1( 800) 2005W yZ x x        21 ( 100) 1620005 x    政府应将每台补贴款额 x 定为 100 元，总收益有最大值． 其最大值为162000元． 113、（2009 年黄石市）正方形 ABCD 在如图所示的平面直角坐标系中， A 在 x 轴正半轴上， D 在 y 轴的 负半轴上， AB 交 y 轴正半轴于 E BC， 交 x 轴负半轴于 F ， 1OE  ，抛物线 2 4y ax bx   过 A D F、 、 三点． （1）求抛物线的解析式；（3 分） （2）Q 是抛物线上 D F、 间的一点，过Q 点作平行于 x 轴的直线交边 AD 于 M ，交 BC 所在直线于 N ， 若 3 2 FQNAFQMS S △四边形 ，则判断四边形 AFQM 的形状；（3 分） （3）在射线 DB 上是否存在动点 P ，在射线CB 上是否存在动点 H ，使得 AP PH⊥ 且 AP PH ，若存 在，请给予严格证明，若不存在，请说明理由．（4 分） O y x B E A D C F 【关键词】正方形的性质；待定系数法；相似三角形判定和性质；特殊平行四边形相关的面积问题；等腰 梯形的判定；全等三角形的性质与判定 【答案】解：（1）依条件有 (0 4)D ， ， (01)E ， ． 由 OEA ADO△ ∽△ 知 2 4OA OE OD  ． ∴ (2 0)A ， 由 Rt RtADE ABF△ ≌ △ 得 DE AF ． ∴ ( 3 0)F  ， ． 将 A F、 的坐标代入抛物线方程， 得 4 2 4 0 9 3 4 0 a b a b        2 3a b   ． ∴抛物线的解析式为 22 2 43 3y x x   ． （2） O y x B E A D C F N M Q 设QM m ， 1 ( 5) | |2 QAFQMS m y  四边形 ， 1 (5 ) | |2FQN QS m y  △ ． ∴ 3( 5) | | (5 ) | | 12Q Qm y m y m      设 ( )Q a b， ，则 ( 1 )M a b ， ∴ 22 2 43 2( 1) 4 b a aa b a         2 2 3 0a a    ， 1a   （舍去 3a  ） 此时点 M 与点 D 重合，QF AM ， AF QM ， AF QM∥ ， 则 AFQM 为等腰梯形． （3）在射线 DB 上存在一点 P ，在射线CB 上存在一点 H ． 使得 AP PH⊥ ，且 AP PH 成立，证明如下： 当点 P 如图①所示位置时，不妨设 PA PH ，过点 P 作 PQ BC⊥ ， PM CD⊥ ， PN AD⊥ ，垂足分 别为 Q M N、 、 ． 若 PA PH ．由 PM PN 得： B A N DMC Q H P ① B A D M C Q H P ② N H N A DC BMP ③ AN PQ ， Rt RtPQH APN △ ≌ △ HPQ PAN   ． 114、22．(2009 年云南省)（本小题 11 分）如图，在平面直角坐标系中，O 是坐标原点，点 A、B 的坐标 分别为 (0 4)A ， 和 ( 2 0)B  ， ，连结 AB ． （1）现将 AOB△ 绕点 A 按逆时针方向旋转 90°得到 1 1AO B△ ，请画出 1 1AO B△ ，并直接写出点 1B 、 1O 的坐标（注：不要求证明）； （2）求经过 B 、 A 、 1O 三点的抛物线对应的函数关系式，并画出抛物线的略图． O x A B y 【关键词】抛物线 二次函数 旋转作图 【答案】解：（1）如图，画出△AO1B1； B1（4，2），O1（4，4）； （2）设所求抛物线对应的函数关系式为 y=a（x-m）2+n， 由 AO1∥x 轴，得 m=2． ∴y=a（x-2）2+n． ∵抛物线经过点 A、B， ∴ 4 4 16 0 . a n a n      ， 解得 1 3 16 .3 a n      ， ∴所求抛物线对应的函数关系式为 21 16( 2)3 3y x    ， 即 21 4 43 3y x x    ． 所画抛物线图象如图所示． 115、（ 2009 年 枣 庄 市 ）24． 如图，抛物线的顶点为 A（2，1），且经过原点 O，与 x 轴的另一个交点为 B． （1）求抛物线的解析式； （2）在抛物线上求点 M，使△MOB 的面积是△AOB 面积的 3 倍； （3）连结 OA，AB，在 x 轴下方的抛物线上是否存在点 N，使△OBN 与△OAB 相似？若存在，求出 N 点的坐标；若不存在，说明理由． 【关键词】二次函数综合题 【答案】（1）由题意，可设抛物线的解析式为 2( 2) 1y a x   ， ∵抛物线过原点， ∴ 2(0 2) 1 0a    ， 1 4a   ． ∴抛物线的解析式为 21 ( 2) 14y x    21 4 x x   ． （2） AOB△ 和所求 MOB△ 同底不等高， 3MOB AOBS S△ △且 ， ∴ MOB△ 的高是 AOB△ 高的 3 倍，即 M 点的纵坐标是 3 ． ∴ 213 4 x x    ，即 2 4 12 0x x   ． 解之，得 1 6x  ， 2 2x   ． ∴满足条件的点有两个： 1(6 3)M ， ， 2 ( 2 3)M  ， ． （3）不存在． 由抛物线的对称性，知 AO AB ， AOB ABO   ． 若 OBN△ 与 OAB△ 相似，必有 BON BOA BNO     ． 设 ON 交抛物线的对称轴于 A点，显然 (2 1)A ， ． y O x A B O1 B1 y x O A B 第 24 题图 y xO A B E N AA′ ∴直线ON 的解析式为 1 2y x  ． 由 21 1 2 4x x x    ，得 1 0x  ， 2 6x  ． ∴ (6 3)N ， ． 过 N 作 NE x 轴，垂足为 E ．在 Rt BEN△ 中， 2BE  ， 3NE  ， ∴ 2 22 3 13NB    ． 又 OB=4， ∴ NB OB ， BON BNO   ， OBN△ 与 OAB△ 不相似． 同理，在对称轴左边的抛物线上也不存在符合条件的 N 点． 所以在该抛物线上不存在点 N，使 OBN△ 与 OAB△ 相似． 116、