2017中考相似三角形练习题及答案 6页

相似三角形分类练习题（1）‎ 一、填空题 ‎1、如图，DE是△ABC的中位线，那么△ADE面积与△ABC面积之比是________。‎ ‎2、如图，△ABC中，DE∥BC，，且，那么＝________。‎ ‎3、如图，△ABC中，∠ACB＝90°，CD⊥AB，D为垂足，AD＝8cm，DB＝2cm，则CD＝________cm。‎ ‎4、如图，△ABC中，D、E分别在AC、AB上，且AD:AB＝AE:AC＝1:2，BC＝5cm，则DE＝________ cm。‎ ‎5、如图，AD、BC相交于点O，AB∥CD，OB＝2cm，OC＝4cm，△AOB面积为4.5cm2，则△DOC面积为___cm2。‎ ‎6、如图，△ABC中，AB＝7，AD＝4，∠B＝∠ACD，则AC＝_______。‎ ‎7、如果两个相似三角形对应高之比为4:5，那么它们的面积比为_____。‎ ‎8、如果两个相似三角形面积之比为1:9，那么它们对应高之比为_____。‎ ‎9、两个相似三角形周长之比为2:3，面积之差为10cm2，则它们的面积之和为_____cm2。‎ ‎10、如图，△ABC中，DE∥BC，AD:DB＝2:3，则＝______。‎ 二、选择题 ‎1、两个相似三角形对应边之比是1:5，那么它们的周长比是（ ）。‎ ‎（A）；（B）1:25；（C）1:5；（D）。‎ ‎2、如果两个相似三角形的相似比为1:4，那么它们的面积比为（ ）。‎ ‎（A）1:16；（B）1:8；（C）1:4；（D）1:2。‎ ‎3、如图，锐角三角形ABC的高CD和高BE相交于O，则与△DOB相似的三角形个数是（ ）。‎ ‎（A）1；（B）2；（C）3；（D）4。‎ 共同 ‎ ‎4、如图，梯形ABCD，AD∥BC，AC和BD相交于O点，＝1:9，则＝（ ）。‎ ‎（A）1:9；（B）1:81；（C）3:1；（D）l:3。‎ 三、如图，△ABC中，DE∥BC，BC＝6，梯形DBCE面积是△ADE面积的2倍，求DE长。‎ 四、如图，△ABE中，AD:DB＝5:2，AC:CE＝4:3，求BF:FC的值。‎ 五、如图，直角梯形ABCD中，AB⊥BC，BC∥AD，BC＜AD，BC＝，AB＝，AC⊥CD，求AD（用的式子表示）‎ 六、如图，△ABC中，点D在BC上，∠DAC＝∠B，BD＝4，DC＝5，DE∥AC交AB于点E，求DE长。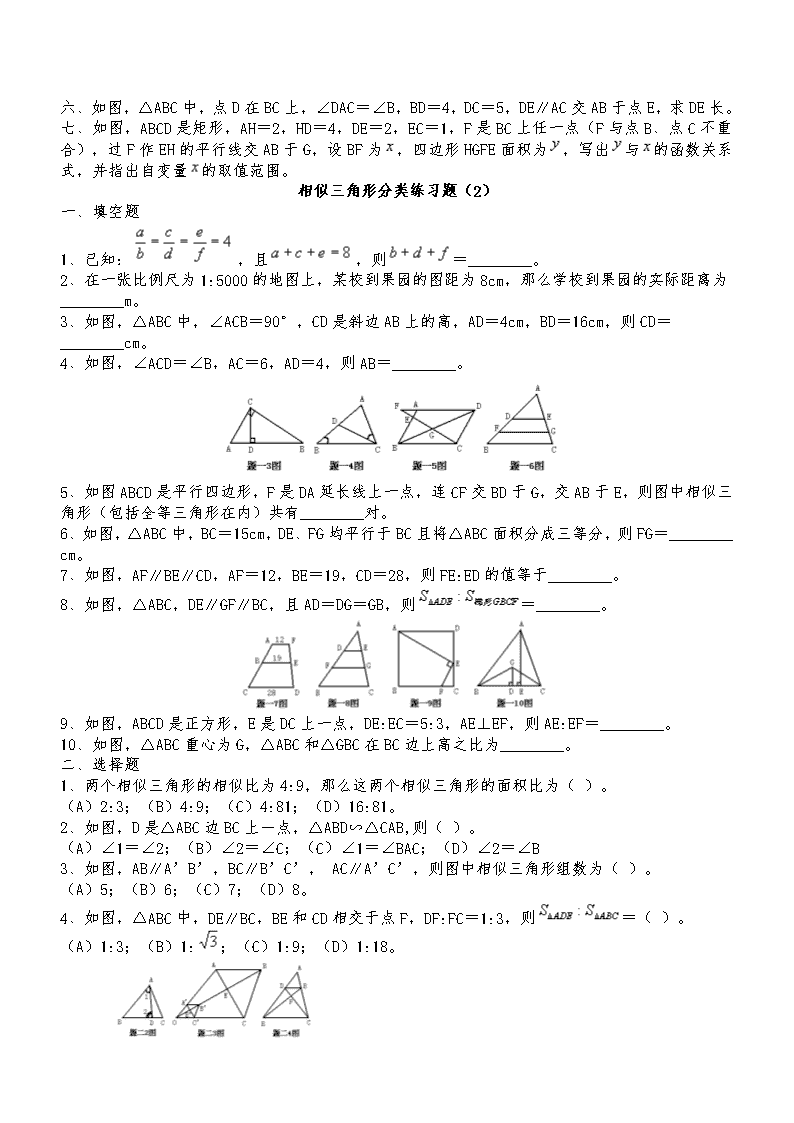‎ 七、如图，ABCD是矩形，AH＝2，HD＝4，DE＝2，EC＝1，F是BC上任一点（F与点B、点C不重合），过F作EH的平行线交AB于G，设BF为，四边形HGFE面积为，写出与的函数关系式，并指出自变量的取值范围。‎ 相似三角形分类练习题（2）‎ 一、填空题 ‎1、已知：，且，则＝________。‎ ‎2、在一张比例尺为1:5000的地图上，某校到果园的图距为8cm，那么学校到果园的实际距离为________m。‎ ‎3、如图，△ABC中，∠ACB＝90°，CD是斜边AB上的高，AD＝4cm，BD＝16cm，则CD＝________cm。‎ ‎4、如图，∠ACD＝∠B，AC＝6，AD＝4，则AB＝________。‎ ‎5、如图ABCD是平行四边形，F是DA延长线上一点，连CF交BD于G，交AB于E，则图中相似三角形（包括全等三角形在内）共有________对。‎ ‎6、如图，△ABC中，BC＝15cm，DE、FG均平行于BC且将△ABC面积分成三等分，则FG＝________ cm。‎ ‎7、如图，AF∥BE∥CD，AF＝12，BE＝19，CD＝28，则FE:ED的值等于________。‎ ‎8、如图，△ABC，DE∥GF∥BC，且AD＝DG＝GB，则＝________。‎ ‎9、如图，ABCD是正方形，E是DC上一点，DE:EC＝5:3，AE⊥EF，则AE:EF＝________。‎ ‎10、如图，△ABC重心为G，△ABC和△GBC在BC边上高之比为________。‎ 二、选择题 ‎1、两个相似三角形的相似比为4:9，那么这两个相似三角形的面积比为（ ）。‎ ‎（A）2:3；（B）4:9；（C）4:81；（D）16:81。‎ ‎2、如图，D是△ABC边BC上－点，△ABD∽△CAB,则（ ）。‎ ‎（A）∠1＝∠2；（B）∠2＝∠C；（C）∠1＝∠BAC；（D）∠2＝∠B ‎3、如图，AB∥A’B’，BC∥B’C’， AC∥A’C’，则图中相似三角形组数为（ ）。‎ ‎（A）5；（B）6；（C）7；（D）8。‎ ‎4、如图，△ABC中，DE∥BC，BE和CD相交于点F，DF:FC＝1:3，则＝（ ）。‎ ‎（A）1:3；（B）1:；（C）1:9；（D）1:18。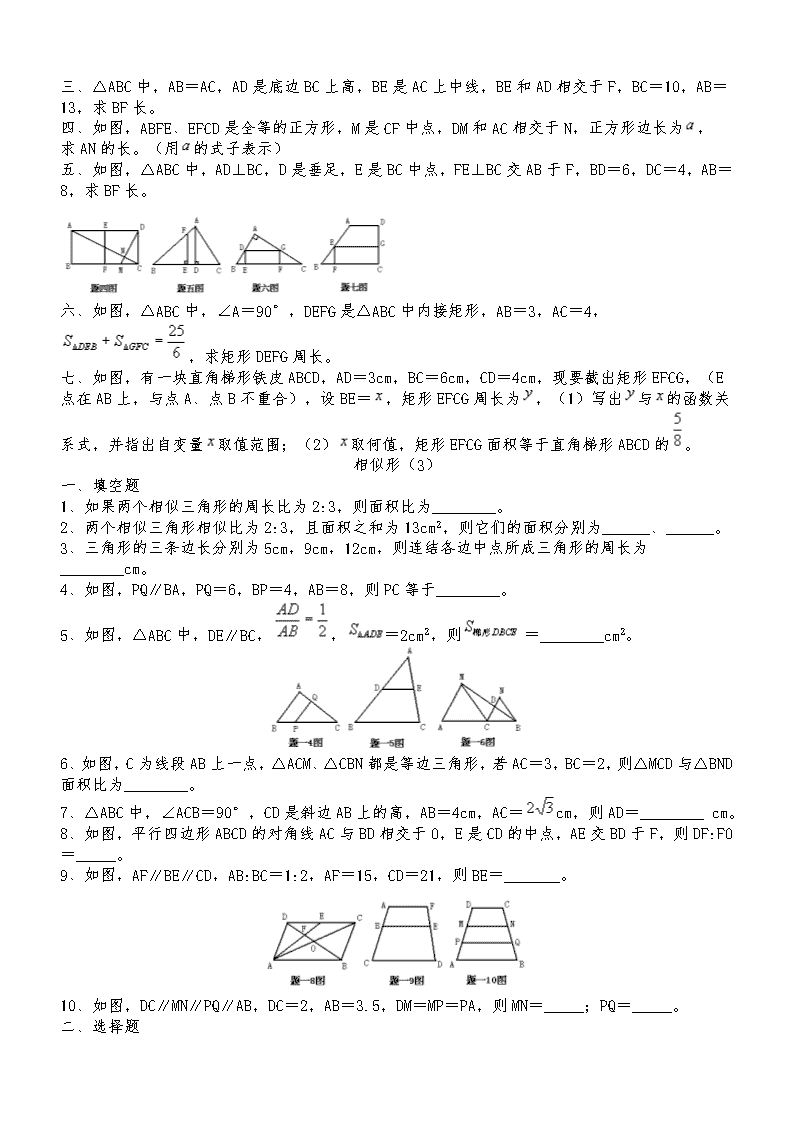 ‎ 三、△ABC中，AB＝AC，AD是底边BC上高，BE是AC上中线，BE和AD相交于F，BC＝10，AB＝13，求BF长。‎ 四、如图，ABFE、EFCD是全等的正方形，M是CF中点，DM和AC相交于N，正方形边长为， 求AN的长。（用的式子表示）‎ 五、如图，△ABC中，AD⊥BC，D是垂足，E是BC中点，FE⊥BC交AB于F，BD＝6，DC＝4，AB＝8，求BF长。‎ 六、如图，△ABC中，∠A＝90°，DEFG是△ABC中内接矩形，AB＝3，AC＝4，，求矩形DEFG周长。‎ 七、如图，有一块直角梯形铁皮ABCD，AD＝3cm，BC＝6cm，CD＝4cm，现要截出矩形EFCG，（E点在AB上，与点A、点B不重合），设BE＝，矩形EFCG周长为，（1）写出与的函数关系式，并指出自变量取值范围；（2）取何值，矩形EFCG面积等于直角梯形ABCD的。‎ 相似形（3）‎ 一、填空题 ‎1、如果两个相似三角形的周长比为2:3，则面积比为________。‎ ‎2、两个相似三角形相似比为2:3，且面积之和为13cm2，则它们的面积分别为______、______。‎ ‎3、三角形的三条边长分别为5cm，9cm，12cm，则连结各边中点所成三角形的周长为 ________cm。‎ ‎4、如图，PQ∥BA，PQ＝6，BP＝4，AB＝8，则PC等于________。‎ ‎5、如图，△ABC中，DE∥BC，，＝2cm2，则＝________cm2。‎ ‎6、如图，C为线段AB上一点，△ACM、△CBN都是等边三角形，若AC＝3，BC＝2，则△MCD与△BND面积比为________。‎ ‎7、△ABC中，∠ACB＝90°，CD是斜边AB上的高，AB＝4cm，AC＝cm，则AD＝________ cm。‎ ‎8、如图，平行四边形ABCD的对角线AC与BD相交于O，E是CD的中点，AE交BD于F，则DF:FO＝_____。‎ ‎9、如图，AF∥BE∥CD，AB:BC＝1:2，AF＝15，CD＝21，则BE＝_______。‎ ‎10、如图，DC∥MN∥PQ∥AB，DC＝2，AB＝3.5，DM＝MP＝PA，则MN＝_____；PQ＝_____。‎ 二、选择题 ‎1、如图，要使△ACD∽△BCA，必须满足（ ）。‎ ‎（A）；（B）；（C）AD2＝CD·BD；（D）AC2＝CD·BC。‎ ‎2、如图，△ABC中，CD⊥AB于D，DE⊥AC于E，∠ACB＝90°，则与△ABC相似的三角形个数为（ ）。‎ ‎（A）2；（B）3；（C）4；（D）5。‎ ‎3、如图，△ABC中，D是AC中点，AF∥DE，＝1:3，则＝（ ）。‎ ‎（A）1:2；（B）2:3；（C）3:4；（D）1:1。‎ ‎4、如图，平行四边形ABCD中，O1、O2、O3为对角线BD上三点，且BO1＝O1O2＝O2O3＝O3D，连结AO1并延长交BC于点E，连结EO3并延长交AD于F，则AD:FD等于（ ）。‎ ‎（A）19:2；（B）9:1；（C）8:1；（D）7:1。‎ 三、如图，已知矩形ABCD中，AB＝10cm，BC＝12cm，E为DC中点，AF⊥BE于点F，求AF长。‎ 四、如图，D、E分别是△ABC边AB和AC上的点，∠1＝∠2，求证：AD·AB＝AE·AC。‎ 五、如图，ABCD是平行四边形，点E在边BA延长线上，连CE交AD于点F，∠ECA＝∠D，求证：AC·BE＝CE·AD。‎ 六、如图，△ABC中，∠ACB＝90°，BC＝8，AC＝12，∠BCD＝30°，求线段CD长。‎ 七、如图，等腰梯形ABCD中，AD∥BC，AB＝DC＝5，AD＝6，BC＝12，E在AD上，AE＝2，F为AB上任一点（点F与点A、点B不重合），过F作EC平行线交BC于G，设BF＝，四边形EFGC面积为，（1）写出与的函数关系式；（2）取何值，EG⊥BC。‎ 相似三角形分类练习题（3）‎ 一、填空题 ‎1、若，则＝________。‎ ‎2、已知，则＝________。‎ ‎3、如图，∠B＝∠ACD，＝2:1，则AC:AB＝________。‎ ‎4、如图，DE∥BC，AD＝4cm，DE＝2cm，BC＝5cm，则AB＝________cm。‎ ‎5、如图，DE∥BC，AD:DB＝1:2，则△ADE与△ABC面积之比为________。‎ ‎6、如图，梯形ABCD中，DC∥EF∥AB，DE＝4，AE＝6，BC＝5，则BF＝________。‎ ‎7、如图，平行四边形ABCD中，对角线AC、BD相交于O，BC＝18，E为OD中点，连结CE并延长交AD于F，则DF＝________。‎ ‎8、如图，△ABC和△BED中，若，且△ABC和△BED周长之差为10cm，则△ABC周长为________cm。‎ ‎9、如图，△ACB∽△ECD，AC:EC＝5:3，＝18，则＝________。‎ ‎10、如图，△ABC中，BE平分∠ABC，BD＝DE，AD＝cm，BD＝2cm，则BC＝________cm。‎ ‎11、如图，ABCD是平行四边形，BC＝2CE，则＝________。‎ ‎12、如图，△ABC中，DE∥BC，BE、CD相交于F，且，则＝________。‎ ‎13、如图，△ABC中，BC＝15cm，DE、FC平行于BC，且将△ABC面积三等分，则DE＋FC＝________ cm。‎ ‎14、将长为cm的线段进行黄金分割，则较长线段与较短线段之差为________ cm。‎ ‎15、如图，平行四边形ABCD中，延长AB到E，使BE＝AB，延长CD到F，使DF＝DC，EF交BC于G，交AD于H，则＝________。‎ 二、选择题 ‎1、如图，△ABC中，DE∥BC，则下列等式中不成立的是（ ）。‎ ‎（A）；（B）；（C）；（D）。‎ ‎2、已知两个相似三角形周长分别为8和6，则它们的面积比为（ ）。‎ ‎（A）4:3；（B）16:9；（C）2:；（D）。‎ ‎3、如图，DE∥BC，AB＝15，AC＝9，BD＝4，则AE长是（ ）。 ‎ ‎（A）；（B）；（C）；（D）。‎ ‎4、如图，DE∥BC，CD和BE相交于O，＝4:9，则AE:EC为（ ）。‎ ‎（A）2:1；（B）2:3；（C）4:9；（D）5:4。‎ ‎5、如图，在边长为的正方形ABCD的一边BC上，任取一点E，作EF⊥AE交CD于点F，如果BE＝，CF＝，那么用的代数式表示是（ ）。‎ ‎（A）；（B）；（C）；（D）。‎ 三、‎ ‎1、已知：，求的值。‎ ‎2、如图，菱形ABCD边长为3，延长AB到E使BE＝2AB，连结EC并延长交AD延长线于点F，求AF的长。‎ ‎3、如图，△ABC中，DE∥BC，＝1:2，BC＝，求DE长。‎ ‎4、如图，直角梯形ABCD中，DA⊥AB，AB∥DC，∠ABC＝60°，∠ABC平分线BE交AD于E，CE⊥BE，BE＝2，求CD长。‎ ‎5、如图，ABCD是边长为的正方形，E是CD中点，AE和BC的延长线相交于F，AE垂直平分线交AE、BC于H、G，求线段FG长。‎ ‎6、如图，△ABC中，AB＞AC，边AB上取一点D，在边AC上取一点E，使AD＝AE，直线DE的延长线和BC延长线交于点P，求证：。‎ 四、（本题8分）‎ 如图，△ABC中，AB＝AC，AD⊥BC，D为垂足，E为AC中点，BE交AD于G，AD＝18cm，BE＝15cm，求△ABC面积。‎ 五、如图，△ABC中，点M在BC边上移动（不与点B、C重合），作ME∥CA交AB于E，作MF∥BA交AC于F，＝10cm2，设，四边形AEMF面积为，写出与的函数关系式，并指出取值范围。‎