2007年中考数学双柏县试卷 12页

双柏县2007年初中毕业考试 ‎ 数 学 试 卷（命题：教研室 郎绍波）‎ ‎（全卷三个大题，共25个小题；考试时间120分钟；满分：120分）‎ 题 号 一 二 三 总 分 得 分 注意：考生可将《2007年云南省高中（中专）招生考试说明与复习指导·数学手册》及科学计算器（品牌和型号不限）带入考场使用.‎ 得分 评卷人 ‎ ‎ 一、选择题（本大题共8个小题，每小题只有一个正确选项，每小题3分，满分24分）‎ ‎1．－2的相反数是（　　）‎ A． B． C． 2 D．－2‎ ‎2．下列运算正确的是（　　）‎ A．x2·x2=x4 B．x6÷x3=x‎2 C．(2x3)3=6x9 D．3x3－2x2=x ‎3．15万勤劳勇敢智慧的双柏人民正在为“建设活力双柏，构建和谐虎乡”而努力奋斗。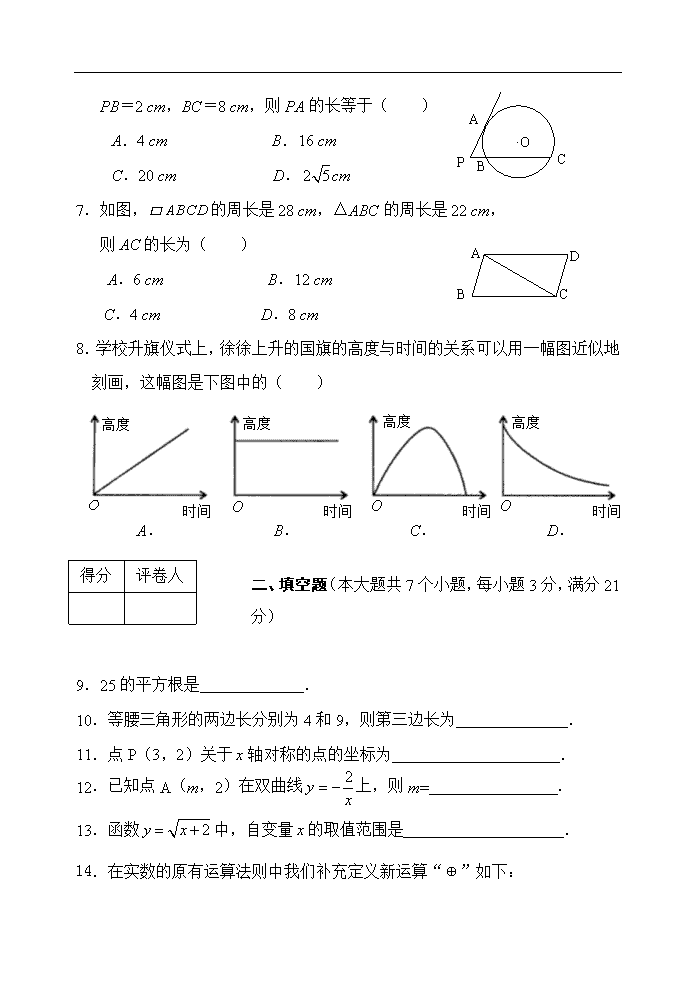15万用科学计数法表示为（　　）‎ A． 1.5×10 B．1.5×‎105 ‎‎ ‎C．15×104 D．1.5×104‎ ‎4．不等式的解集是（　　）‎ A．　　　　B． C．　　　 　D．‎ ‎5．在同一坐标系中一次函数和二次函数的图象可能为（ ）‎ O x y O x y O x y O x y A B C D ‎6．如图，已知PA是⊙O的切线，A为切点，PC与⊙O相交于B、C两点，‎ A ‎·O P C B PB＝‎2 cm，BC＝‎8 cm，则PA的长等于（　　）‎ A．‎4 cm B．‎16 cm ‎ C．‎20 cm D．cm ‎7．如图，的周长是‎28 cm，△ABC的周长是‎22 cm，‎ A B C D 则AC的长为（　　）‎ A．‎6 cm　 　　B．‎‎12 cm ‎　 C．‎4 cm　 　 　D．‎‎8 cm ‎8．学校升旗仪式上，徐徐上升的国旗的高度与时间的关系可以用一幅图近似地刻画，这幅图是下图中的（　　）‎ 时间 A．‎ 高度 时间 B．‎ 高度 时间 C．‎ 高度 时间 D．‎ 高度 得分 评卷人 ‎ ‎ 二、填空题（本大题共7个小题，每小题3分，满分21分）‎ ‎9．25的平方根是 ．‎ ‎10．等腰三角形的两边长分别为4和9，则第三边长为 ．‎ ‎11．点P（3，2）关于x轴对称的点的坐标为_____________________．‎ ‎12．已知点A（m，2）在双曲线上，则m= ．‎ ‎13．函数中，自变量的取值范围是 ．‎ ‎14．在实数的原有运算法则中我们补充定义新运算“⊕”如下：‎ 当a≥b时，a⊕b＝b2；当a＜b时，a⊕b＝a．则当x＝2时，‎ D A C B O ‎（1⊕x）－（3⊕x）的值为 ．‎ ‎15．如图，⊙O是等边三角形ABC的外接圆，‎ 点D是⊙O上一点，则∠BDC = ．‎ 得分 评卷人 三、解答题（本大题共10个小题，满分75分）‎ 得分 评卷人 ‎16．（本小题6分）化简：‎ 得分 评卷人 ‎17．（本小题6分）如图，在梯形纸片ABCD中，AD//BC，AD>CD，将纸片沿过点D的直线折叠，使点C落在AD上的点C处，折痕DE交BC于点E，连结C′E．‎ A D E B C C′‎ 求证：四边形CDC′E是菱形．‎ 得分 评卷人 ‎18．（本小题6分）解分式方程：‎ 得分 评卷人 ‎19．（本小题7分）如图，AB是⊙O的直径，CB是弦，‎ OD⊥CB于E，交于D，连接AC．‎ ‎（1）请写出两个不同类型的正确结论；（2分） ‎ A D E C O B ‎（2）若CB=8，ED=2，求⊙O的半径．（5分）‎ 得分 评卷人 ‎ ‎ ‎20．（本小题6分）已知△ABC的三个顶点坐标如下表：‎ ‎（1）将下表补充完整，并在直角坐标系中，画出△；‎ ‎（，）‎ ‎ （，）‎ A （2，1）‎ ‎（ 4 ，2 ）‎ B （4，3）‎ ‎（ ， ）‎ C （5，1）‎ ‎（ ， ）‎ ‎（2）观察△ABC与△，写出有关这两个三角形关系的一个正确结论。‎ 答：‎ 得分 评卷人 ‎ ‎ B C E F A ‎21．（本小题6分）如图，在某建筑物AC上，挂着“多彩云南”的宣传条幅BC，小明站在点F处，看条幅顶端B，测的仰角为，再往条幅方向前行‎20米到达点E处，看到条幅顶端B，测的仰角为，求宣传条幅BC的长，（小明的身高不计，结果精确到‎0.1米）‎ ‎ ‎ 得分 评卷人 ‎22．（本题7分）某数学老师为了了解学生在数学学习中常见错误的纠正情况，收集了学生在作业和考试中的常见错误，编制了10道选择题，每题3分，对她所任教的初三（1）班和（2）班进行了检测．如图表示从两班各随机抽取的10名学生的得分情况：‎ ‎（1）利用图中提供的信息，补全下表：（3分)‎ 班级 平均数（分）‎ 中位数（分）‎ 众数（分）‎ ‎（1）班 ‎24‎ ‎24‎ ‎（2）班 ‎24‎ ‎（2）若把24分以上（含24分）记为“优秀”，两班各有40名学生，请估计两班各有多少名学生成绩优秀；（2分）‎ ‎（3）观察图中的数据分布情况，你认为哪个班的学生纠错的整体情况更好一些？（2分）‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 编号 成绩（分)‎ ‎3‎ ‎6‎ ‎9‎ ‎12‎ ‎15‎ ‎18‎ ‎21‎ ‎24‎ ‎27‎ ‎30‎ ‎（1）班 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 编号 成绩（分)‎ ‎3‎ ‎6‎ ‎9‎ ‎12‎ ‎15‎ ‎18‎ ‎21‎ ‎24‎ ‎27‎ ‎30‎ ‎（2）班 得分 评卷人 ‎23．（本小题10分）阅读下列材料，并解决后面的问题．‎ 材料：一般地，n个相同的因数相乘：。如23=8，此时，3叫做以2为底8的对数，记为。‎ 一般地，若，则n叫做以为底b的对数，记为，则4叫做以3为底81的对数，记为。‎ ‎ 问题：‎ ‎（1）计算以下各对数的值：（3分）‎ ‎ .‎ ‎（2）观察（1）中三数4、16、64之间满足怎样的关系式？ 之间又满足怎样的关系式？（2分）‎ ‎（3）由（2）的结果，你能归纳出一个一般性的结论吗？（2分）‎ ‎ ‎ ‎（4）根据幂的运算法则：以及对数的含义证明上述结论。（3分）‎ ‎ 证明：‎ 得分 评卷人 ‎24．（本小题9分）某电信公司开设了甲、乙两种市内移动通信业务。甲种使用者每月需缴15元月租费，然后每通话1分钟, 再付话费0.3元； 乙种使用者不缴月租费, 每通话1分钟, 付话费0.6元。若一个月内通话时间为x分钟, 甲、乙两种的费用分别为y1和y2元。‎ ‎(1)试分别写出y1、y2与x之间的函数关系式； ‎ ‎(2)在同一坐标系中画出y1、y2的图像；‎ ‎(3)根据一个月通话时间，你认为选用哪种通信业务更优惠？‎ 得分 评卷人 ‎25．（本小题10分）如图所示，在平面直角坐标中，四边形OABC是等腰梯形，CB∥OA，OA=7，AB=4，∠COA=60°，点P为x轴上的—个动点，点P不与点0、点A重合．连结CP，过点P作PD交AB于点D．‎ ‎(1)求点B的坐标；‎ ‎(2)当点P运动什么位置时，△OCP为等腰三角形，求这时点P的坐标；‎ ‎(3)当点P运动什么位置时，使得∠CPD=∠OAB，且，求这时点P的坐标．‎ O y P C B D A x 双柏县2007年初中毕业考试 数学试卷参考答案 一、选择题（本大题共8个小题，每小题只有一个正确选项，每小题3分，满分24分）‎ ‎1．C 2．A 3． B 4．C 5．A 6．D 7．D 8．A 二、填空题（本大题共7个小题，每小题3分，满分21分）‎ ‎9．±5 10．9 11．（3，－2） 12．－1 13．x≥－2 14．－3 15．60°‎ 三、解答题（本大题共10个小题，满分75分）‎ ‎16．（本小题6分）‎ 解：原式＝÷ ＝· ＝x A D E B C C′‎ ‎17．（本小题6分）‎ 证明：根据题意可知 ‎ 则 ‎ ‎∵AD//BC ∴∠C′DE=∠CED ‎∴∠CDE=∠CED ∴CD=CE ‎ ‎∴CD=C′D=C′E=CE ∴四边形CDC′E为菱形。‎ ‎18．（本小题6分）解分式方程：‎ 解： ‎ ‎ ‎ ‎ ‎ 经检验 是原方程的解 ∴ ‎ ‎19．（本小题7分）‎ ‎（1）不同类型的正确结论有：①BE=CE；②BD=CD；③∠BED=90°；④∠BOD=∠A；⑤AC//OD；⑥AC⊥BC；⑦；⑧；‎ ‎⑨△BOD是等腰三角形；⑩；等等。‎ ‎（说明：每写对一条给1分，但最多只给2分）‎ A D E C O B ‎（2）∵ OD⊥CB ∴BE=CE==4‎ 设的半径等于R，则OE=OD－DE=R－2‎ 在Rt△OEB中，由勾股定理得，‎ ‎ 即 解得R=5 ∴⊙O的半径为5‎ ‎20．（本小题8分）‎ 解（1）‎ ‎（，）‎ ‎ （，）‎ A （2，1）‎ ‎（ 4 ，2 ）‎ B （4，3）‎ ‎（ 8 ，6 ）‎ C （5，1）‎ ‎（10 ，2 ）‎ 正确写出一个点的坐标各得1分 正确画出△得3分 ‎(2)出有关两三角形形状、大小、位置等关系，‎ B C E F A 如△ABC∽△、周长比、相似比、位似比等均给3分 ‎21．（本小题6分）‎ 解： ∵∠BFC =，∠BEC =，∠BCF =‎ ‎ ∴∠EBF =∠EBC =‎ ‎ ∴BE = EF = 20‎ ‎ 在Rt⊿BCE中，‎ ‎ ‎ 答：宣传条幅BC的长是‎17.3米。‎ ‎22．（本题7分）‎ 解：（1）‎ 班级 平均数（分）‎ 中位数（分）‎ 众数（分）‎ ‎（1）班 ‎24‎ ‎（2）班 ‎24‎ ‎21‎ ‎　　　　‎ ‎（2）∵（名），（名）．‎ ‎∴（1）班有28名学生成绩优秀，（2）班有24名学生成绩优秀．‎ ‎（3） （1）班的学生纠错的整体情况更好一些．‎ ‎23．（本小题10分）‎ ‎（1） ， ，‎ ‎（2）4×16=64 ， + = ‎ ‎（3） + = ‎ ‎（4）证明：设=b1 , =b2‎ 则， ‎ ‎∴ ‎ ‎∴b1+b2= 即 + = ‎ ‎24．（本小题9分）‎ 解:（1）y1=15+0.3x (x≥0)‎ y2=0.6x (x≥0)‎ ‎（2）如下图：‎ ‎ ‎ ‎（3）由图像知：‎ 当一个月通话时间为50分钟时, 两种业务一样优惠 当一个月通话时间少于50分钟时, 乙种业务更优惠 当一个月通话时间大于50分钟时, 甲种业务更优惠 ‎【说明： 用方程或不等式求解进行分类讨论也可】‎ y O P C B D A x Q ‎25．（本小题10分）‎ ‎（1）过B作BQ⊥OA于Q则∠COA=∠BAQ=60°‎ 在Rt△BQA中， QB=ABSin60°=‎ ‎∴OQ=OA－QA=5 ∴B（5，） ‎ D O y P C B A x P ‎（2）若点P在x正半轴上 ‎∵∠COA=60°，△OCP为等腰三角形 ‎∴△OCP是等边三角形 ‎ ‎∴OP=OC=CP=4 ∴P（4，0）‎ 若点P在x负半轴上 ‎ ‎∵∠COA=60° ∴∠COP=120° ‎ ‎∴△OCP为顶角120°的等腰三角形 ‎∴OP=OC=4 ∴P（－4，0）‎ ‎∴点P的坐标为（4，0）或（－4，0）‎ ‎（3）∵∠CPD=∠OAB=∠COP=60°‎ O y P C B D A x ‎∴∠OPC+∠DPA=120°‎ 又∵∠PDA+∠DPA=120°‎ ‎∴∠OPC=∠PDA ‎∵∠OCP=∠A=60°‎ ‎∴△COP∽△PAD ‎ ‎∴ ‎ ‎∵，AB=4‎ O y P C B D A x ‎∴BD= ∴AD=‎ 即 ‎ ‎∴‎ 得OP=1或6‎ x ‎∴P点坐标为（1，0）或（6，0）‎