2016枣庄中考数学试题含解析 14页

‎ 二○一六年枣庄市初中学业水平考试 数 学 试 题 第Ⅰ卷 (选择题 共36分)‎ 一、选择题：本大题共12小题，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来．每小题选对得３分，选错、不选或选出的答案超过一个均计零分．‎ ‎1.下列计算，正确的是 ‎ A． B． C． D． ‎ 第２题图 ‎2.如图，∠AOB的一边OA为平面镜，∠AOB=37°36′，在 OB上有一点E，从E点射出一束光线经OA上一点D 反射，反射光线DC恰好与OB平行，则∠DEB的度数 是 A．75°36′ B．75°12′ C．74°36′ D．74°12′‎ ‎3.某中学篮球队12名队员的年龄如下表：‎ 年龄:（岁）‎ ‎13‎ ‎14‎ ‎15‎ ‎16‎ 人数 ‎1‎ ‎5‎ ‎4‎ ‎2‎ ‎ 关于这12名队员的年龄，下列说法错误的是 ‎　A．众数是14 B.极差是3 C．中位数是14.5 D．平均数是14.8‎ 第4题图 ‎4.如图，在△ABC中，AB = AC，∠A = 30°，E为BC延长线上 一点，∠ABC与∠ACE的平分线相交于点D，则∠D等于 A．15° B．17.5° C．20° D．22.5°‎ ‎5.已知关于x的方程有一个根为-2，则另一个根为 A．5 B．－1 C．2 D．－5‎ ‎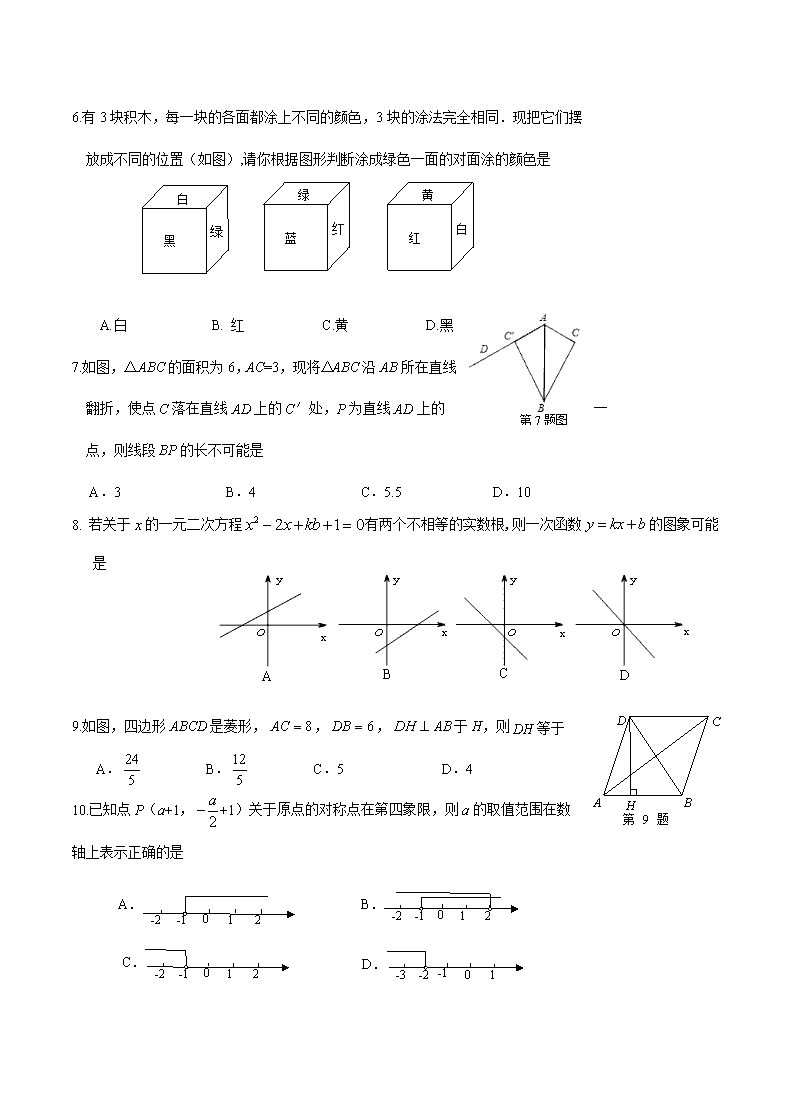6.有3块积木，每一块的各面都涂上不同的颜色，3块的涂法完全相同．现把它们摆 放成不同的位置（如图）,请你根据图形判断涂成绿色一面的对面涂的颜色是 绿 白 黑 红 绿 蓝 白 黄 红 ‎ ‎ 第7题图 A.白 　　　　 B. 红 　　　　 C.黄 　　　　 D.黑 ‎7.如图，△ABC的面积为6，AC=3，现将△ABC沿AB所在直线 翻折，使点C落在直线AD上的C′处，P为直线AD上的一 点，则线段BP的长不可能是 ‎　 A．3 　　 B．4 C．5.5 D．10 ‎ BV A CV DV ‎8. 若关于的一元二次方程有两个不相等的实数根,则一次函数的图象可能是 ‎ 第9题图 A B C D H ‎9.如图，四边形ABCD是菱形，，，于H，则DH等于 A． B． C．5 D．4‎ ‎10.已知点P（a+1，+1）关于原点的对称点在第四象限，则a的取值范围在数轴上表示正确的是 ‎-2‎ ‎-1‎ ‎2‎ ‎1‎ ‎0‎ B．‎ ‎-2‎ ‎-1‎ ‎2‎ ‎1‎ ‎0‎ A．‎ ‎-2‎ ‎-1‎ ‎2‎ ‎1‎ ‎0‎ C．‎ ‎-3‎ ‎-2‎ ‎1‎ ‎0‎ ‎-1‎ D．‎ ‎ ‎ 第11题图 ‎11. 如图，AB是⊙O的直径，弦CD⊥AB，∠CDB＝30°，CD ‎＝，则阴影部分的面积为 ‎ A．2π B．π C. D.‎ 第12题图 ‎12.已知二次函数（）的图象如图所示，‎ 给出以下四个结论：①；②；③；‎ ‎④.其中，正确的结论有 A.1个 B.2个 C.3个 D.4个 第Ⅱ卷 (非选择题 共84分)‎ 二、填空题：本大题共6小题，满分24分．只填写最后结果，每小题填对得4分． ‎ ‎13. 计算： ．‎ ‎14. 如图是矗立在高速公路边水平地面上的交通警示牌，经测量得到如下数据：AM=4米，AB=8米，∠MAD=45°，∠MBC=30°，则警示牌的高CD为　 　米（结果精确到0.1米，参考数据： =1.41，=1.73）．‎ 第15题图 第14题图 ‎15. 如图，在半径为3的⊙O中，直径AB与弦CD相交于点E，连接AC，BD，若AC=2，则tanD=　 　 . ‎ ‎16. 如图，点 A的坐标为（-4,0），直线与坐标轴交于点B，C，连结 AC，如果∠ACD =90°，则n的值为 .‎ B′‎ A C′‎ C B 第17题图 第16题图 ‎17. 如图，已知△ABC中，∠C=90°，AC=BC=，将△ABC绕点A顺时针方向旋 转60°到△AB′C′的位置，连接C′B，则C′B= .‎ ‎18. 一列数，，，… 满足条件：，（n≥2，且n为整 数），则 =　 　．‎ 三、解答题：本大题共7小题，满分60分．解答时，要写出必要的文字说明、证 明过程或演算步骤． ‎ ‎ 　 19．(本题满分8分) ‎ 先化简，再求值：，其中a是方程的解.‎ ‎20. (本题满分8分)‎ 表示n边形的对角线的交点个数（指落在其内部的交点），如果这些交点都不重合，那么与n的关系式是： (其中，a，b是常数，n≥4)‎ ‎⑴通过画图，可得四边形时，＝　　　(填数字)；五边形时，＝　　　(填数字).‎ ‎⑵请根据四边形和五边形对角线交点的个数，结合关系式，求a，b的值.‎ ‎21．（本题满分8分）‎ 小军同学在学校组织的社会实践活动中，负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了50户居民的月均用水量（单位：t）,并绘制了样本的频数分布表：‎ 月 均 用水量 频数 ‎2‎ ‎12‎ ‎①‎ ‎10‎ ‎②‎ ‎3‎ ‎2‎ 百分比 ‎4%‎ ‎24%‎ ‎30%‎ ‎20%‎ ‎③‎ ‎6%‎ ‎4%‎ ‎⑴请根据题中已有的信息补全频数分布表：① ，② ，③ ；‎ ‎⑵如果家庭月均用水量“大于或等于5t且小于8t”为中等用水量家庭，请你通过样本估计总体中的中等用水量家庭大约有多少户？‎ ‎⑶记月均用水量在范围内的两户为、，在范围内3户为、、，从这5户家庭中任意抽取2户，试完成下表，并求出抽取的2户家庭来自不同范围的概率.‎ ‎22．(本题满分８分)‎ 第22题图 如图，在矩形OABC中，OA=3，OC=2，F是AB上的一个动点（F不与A，B重合），过点F的反比例函数的图象与BC边交于点E．‎ ‎⑴当F为AB的中点时，求该函数的解析式；‎ ‎⑵当k为何值时，△EFA的面积最大，最大面积是多少？‎ ‎23．(本题满分8分) ‎ 如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接PA，PB，AB，已知∠PBA=∠C．‎ ‎⑴求证：PB是⊙O的切线；‎ ‎⑵连接OP，若OP∥BC，且OP=8，⊙O的半径为，求BC的长．‎ 第23题图 ‎ ‎ ‎24.(本题满分10分) ‎ 如图，把△EFP放置在菱形ABCD中，使得顶点E，F，P分别在线段AB，AD，AC上，已知EP=FP=6，EF=，∠BAD=60°，且AB＞．‎ ‎⑴求∠EPF的大小；‎ ‎⑵若AP=8，求AE+AF的值；‎ 第24题图 D C E F A B P ‎⑶若△EFP的三个顶点E，F，P分别在线段AB，AD，AC上运动，请直接写出AP长的最大值和最小值. ‎ 第24题备用图 D C A B ‎25. (本题满分10分)‎ ‎ 如图，已知抛物线y＝ax2＋bx＋c(a≠0)的对称轴为直线x＝－1，且经过A（1，0），C（0，3）两点，与x轴的另一个交点为B.‎ ‎⑴若直线y＝mx＋n经过B，C两点，求直线BC和抛物线的解析式；‎ 第25题图 ‎⑵在抛物线的对称轴x＝－1上找一点M，使点M到点A的距离与到点C的距离之和最小，求点M的坐标；‎ ‎⑶设点P为抛物线的对称轴x＝－1上的一个动点，求使△BPC为直角三角形的点P的坐标．‎ ‎ ‎ 绝密☆启用前 二○一六年枣庄市初中学业水平考试 数学参考答案及评分意见 ‎ 评卷说明：‎ ‎ 1．选择题和填空题中的每小题，只有满分和零分两个评分档，不给中间分．‎ ‎ 2．解答题每小题的解答中所对应的分数，是指考生正确解答到该步所应得的累计分数．本答案中每小题只给出一种解法，考生的其他解法，请参照评分意见进行评分．‎ ‎ 3．如果考生在解答的中间过程出现计算错误，但并没有改变试题的实质和难度，其后续部分酌情给分，但最多不超过正确解答分数的一半，若出现较严重的逻辑错误，后续部分不给分．‎ 一、选择题：(本大题共12小题，每小题3分，共36分)‎ 题 号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答 案 C B D A B C A B A C D C 二、填空题：(本大题共6小题，每小题4分，共24分)‎ ‎13． 14．2.9　 15． 16． 17． 18．－1 ‎ 三、解答题：(本大题共7小题，共60分)‎ ‎ 19．(本题满分8分)‎ ‎ 解：原式=……………………………………………………2分 ‎ =‎ ‎ =…………………………………………………………………………4分 ‎ 由，得 ， ………………………………………6分 又 ∴．‎ ‎∴原式=． ………………………………………………………………8分 ‎20．(本题满分8分)‎ 解：⑴由画图，可得 当时，；当时，. ………………………………………4分 ‎⑵将上述数值代入公式，得 ‎ ………………………………………………6分 解之，得………………………………………………………………………8分 ‎21.(本题满分8分)‎ ‎ 解：⑴①15 ②6 ③12% ………………………………………………………3分 ‎⑵中等用水量家庭大约有450×（20%+12%+6%）=171（户） ……………………5分 ‎⑶表格（略），抽取的2户家庭来自不同范围的概率 ‎ P=． …………………………………………………………………8分 第22题图 ‎22．(本题满分8分)‎ ‎ 解：⑴在矩形OABC中，OA=3，OC=2，‎ ‎∴B（3，2），‎ ‎∵F为AB的中点，∴F（3，1）. …………2分 ‎∵点F在反比例函数的图象上，‎ ‎∴k=3.‎ ‎∴该函数的解析式为. ………4分 ‎⑵由题意，知E，F两点坐标分别为E（，2），F（3，），‎ ‎∴ …………………………6分 所以当k=3时，S有最大值，S最大值=． ……………………………………8分 第23题图 23． ‎(本题满分8分)‎ ‎ ⑴证明：如图所示，连接OB.‎ ‎∵AC是⊙O的直径，‎ ‎∴∠ABC=90°，∠C+∠BAC=90°. ……………1分 ‎∵OA=OB，‎ ‎∴∠BAC=∠OBA. ………………………2分 ‎∵∠PBA=∠C，‎ ‎∴∠PBA+∠OBA=90°，即PB⊥OB.‎ ‎∴PB是⊙O的切线． ……………………………4分 ‎⑵解：⊙O的半径为，∴OB=，AC=．‎ ‎∵OP∥BC，‎ ‎∴∠BOP=∠OBC=∠C.‎ 又∵∠ABC=∠PBO=90°，‎ ‎∴△ABC∽△PBO，…………………………………………………………………………6分 ‎∴，即.‎ ‎∴BC=2．……………………………………………………………………………………8分 23． ‎(本题满分10分) ‎ N M 第24题图 D C E F A B G P 解：（1）如图，过点P作PG⊥EF于G.‎ ‎∵PE=PF=6，EF=，‎ ‎∴FG=EG=，‎ ‎∠FPG=∠EPG=.‎ 在Rt△FPG中，sin∠FPG=.‎ ‎∴∠FPG=60°, ‎ ‎∴∠EPF=2∠FPG=120°. ……………………………………………………3分 ‎(2)作PM⊥AB于M，PN⊥AD于N．‎ ‎∵AC为菱形ABCD的对角线，‎ ‎∴∠DAC=∠BAC，AM=AN，PM=PN.‎ ‎ 在Rt△PME和Rt△PNF 中，PM=PN，PE=PF，‎ ‎∴Rt△PME≌Rt△PNF ‎∴NF=ME. ………………………………………………………………………………5分 又AP=10，,‎ ‎∴AM= AN =APcos30°==.‎ 第24题备用图 D C A B E P1‎ F P2‎ O ‎∴AE＋AF=（AM＋ME）＋(AN－NF)=AM＋AN=.………………………………7分 ‎(3) 如图，当△EFP的三个顶点E，F，P分别在线段AB，AD，AC上运动时，点P在，之间运动，易知，，‎ ‎∴AP的最大值为12，AP的最小值为6.……………………………………10分 ‎25．(本题满分10分)‎ ‎ 解：（1）依题意，得　解之，得 ‎∴抛物线解析式为． …………………………………………2分 第25题图 ‎ ∵对称轴为x＝－1，且抛物线经过A（1，0），‎ ‎∴B（－3，0）．‎ 把B（－3，0）、C（0，3）分别直线y＝mx＋n，得 ‎ 解之，得 ‎ ‎∴直线BC的解析式为． …………3分 ‎（2）∵MA=MB，∴MA+MC=MB+MC.‎ ‎∴使MA+MC最小的点M应为直线BC与对称轴x＝‎ ‎－1的交点.‎ ‎ 设直线BC与对称轴x＝－1的交点为M，把x＝－1‎ 代入直线，得y＝2.‎ ‎ ∴M（－1，2）………………………………………………………………………6分 ‎ （3）设P（－1，t），结合B（－3，0），C（0， 3），得 BC2＝18，‎ ‎ PB2＝(－1＋3)2＋t2＝4＋t2，‎ ‎ PC2＝(－1)2＋(t－3)2＝t2－6t＋10.‎ ‎①若B为直角顶点，则BC2＋PB2＝PC2，即 ‎ ‎ 18＋4＋t2＝t2－6t＋10. 解之,得t＝－2.‎ ② 若C为直角顶点，则BC2＋PC2＝PB2，即 ‎ 18＋t2－6t＋10＝4＋t2．解之，得t＝4．‎ ③ 若P为直角顶点，则PB2＋PC2＝BC2，即 ‎ 4＋t2＋t2－6t＋10＝18．解之，得t1＝，t2＝．‎ ‎ 综上所述，满足条件的点P共有四个,分别为 ‎ (－1，－2), (－1，4), (－1，) ,(－1，)．…10分