中考数学专题复习七统计与概率的实际应用题 4页

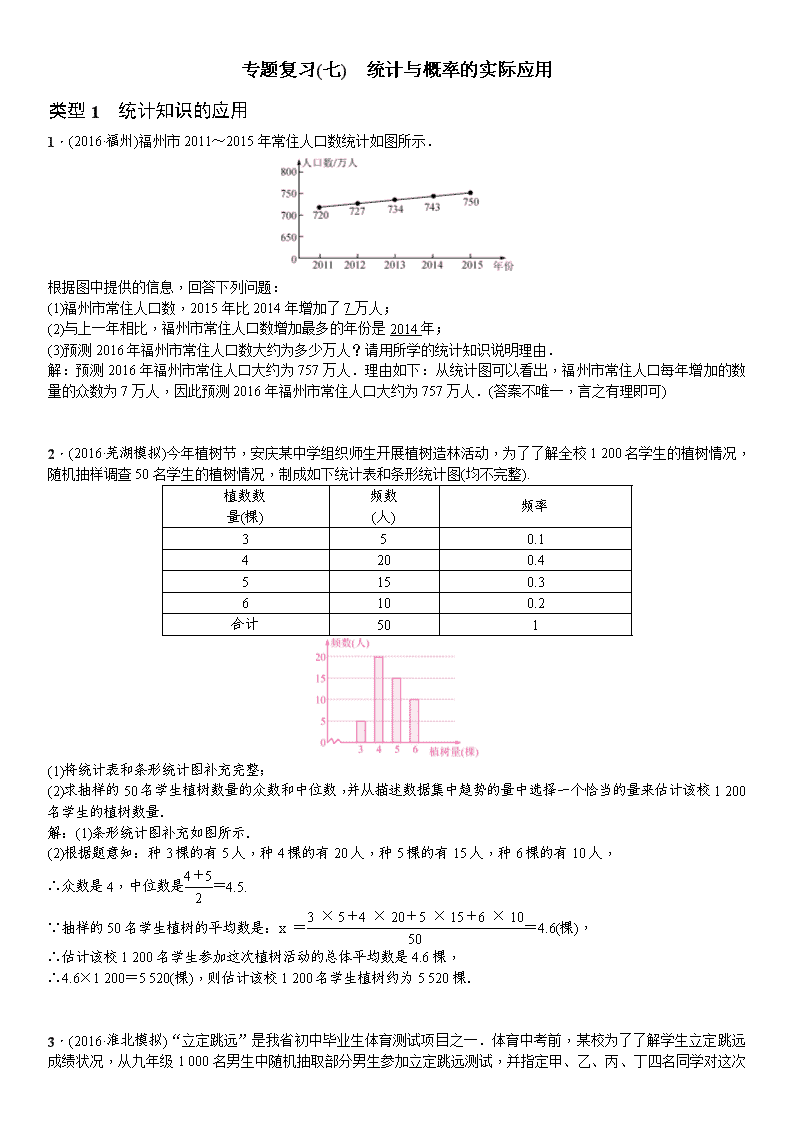
专题复习(七)　统计与概率的实际应用 类型1　统计知识的应用 ‎1．(2016·福州)福州市2011～2015年常住人口数统计如图所示．‎ 根据图中提供的信息，回答下列问题：‎ ‎(1)福州市常住人口数，2015年比2014年增加了7万人；‎ ‎(2)与上一年相比，福州市常住人口数增加最多的年份是2014年；‎ ‎(3)预测2016年福州市常住人口数大约为多少万人？请用所学的统计知识说明理由．‎ 解：预测2016年福州市常住人口大约为757万人．理由如下：从统计图可以看出，福州市常住人口每年增加的数量的众数为7万人，因此预测2016年福州市常住人口大约为757万人．(答案不唯一，言之有理即可)‎ ‎2．(2016·芜湖模拟)今年植树节，安庆某中学组织师生开展植树造林活动，为了了解全校1 200名学生的植树情况，随机抽样调查50名学生的植树情况，制成如下统计表和条形统计图(均不完整).‎ 植数数 量(棵)‎ 频数 ‎(人)‎ 频率 ‎3‎ ‎5‎ ‎0.1‎ ‎4‎ ‎20‎ ‎0.4‎ ‎5‎ ‎15‎ ‎0.3‎ ‎6‎ ‎10‎ ‎0.2‎ 合计 ‎50‎ ‎1‎ ‎(1)将统计表和条形统计图补充完整；‎ ‎(2)求抽样的50名学生植树数量的众数和中位数，并从描述数据集中趋势的量中选择一个恰当的量来估计该校1 200名学生的植树数量．‎ 解：(1)条形统计图补充如图所示．‎ ‎(2)根据题意知：种3棵的有5人，种4棵的有20人，种5棵的有15人，种6棵的有10人，‎ ‎∴众数是4，中位数是＝4.5.‎ ‎∵抽样的50名学生植树的平均数是：x ＝＝4.6(棵)，‎ ‎∴估计该校1 200名学生参加这次植树活动的总体平均数是4.6棵，‎ ‎∴4.6×1 200＝5 520(棵)，则估计该校1 200名学生植树约为5 520棵．‎ ‎3．(2016·淮北模拟)“立定跳远”是我省初中毕业生体育测试项目之一．体育中考前，某校为了了解学生立定跳远成绩状况，从九年级1 000名男生中随机抽取部分男生参加立定跳远测试，‎ 并指定甲、乙、丙、丁四名同学对这次测试结果的数据作出整理，下图是这四名同学提供的部分信息：‎ ‎ 甲：将全体测试数据分成6组绘成直方图(如图)；‎ ‎ 乙：立定跳远成绩不少于5分的同学占96%；‎ ‎ 丙：第①、②两组频率之和为0.12，且第②组与第⑥组频数都是12；‎ ‎ 丁：第②、③、④组的频数之比为4∶17∶15.‎ 根据这四名同学提供的材料，请解答如下问题：‎ 每组数据含左端点值不含右端值(最后一组除外)‎ ‎(1)这次立定跳远测试共抽取多少名学生？各组各有多少人？‎ ‎(2)如果立定跳远不少于11分为优秀，根据这次抽查的结果，估计全年级达到立定跳远优秀的人数为多少？‎ ‎(3)以每组的组中值(每组的中点对应的数据)作为这组立定跳远成绩的代表，估计这批学生立定跳远分数的平均值．‎ 解：(1)∵立定跳远成绩不少于5分的同学占96%，即②③④⑤⑥组人数占96%，‎ 第①组频率为：1－96%＝0.04.‎ ‎∵第①、②两组频率之和为0.12，‎ ‎∴第②组频率为：0.12－0.04＝0.08.‎ 又∵第②组频数是12，‎ ‎∴这次立定跳远测试共抽取学生人数为：12÷0.08＝150(人)．‎ ‎∵②、③、④组的频数之比为4∶17∶15，‎ ‎∴12÷4＝3(人)，‎ ‎∴可算得第①～⑥组的人数分别为：①150×0.04＝6(人)，②4×3＝12(人)，③17×3＝51(人)，④15×3＝45(人)，⑥与②相同，为12人，⑤为150－6－12－51－45－12＝24(人)．‎ 答：这次立定跳远测试共抽取150名学生，各组的人数分别为6，12，51，45，24，12.‎ ‎(2)第⑤、⑥两组的频率之和为＝＝0.24，‎ ‎1 000×0.24＝240(人)‎ 答：估计全年级达到立定跳远优秀的有240人．‎ ‎(3)＝＝9.4(分)．‎ 答：这批学生立定跳远的分数的平均值约为9.4分．‎ 类型2　概率知识的应用 ‎4．(2016·宜昌)某小学学生较多，为了便于学生尽快就餐，师生约定：早餐一人一份，一份两样，一样一个．食堂师傅在窗口随机发放(发放的食品价格一样)．食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品．‎ ‎(1)按约定，“小李同学在该天早餐得到两个油饼”是不可能(可能，必然，不可能)事件．‎ ‎(2)请用列表或画树状图的方法，求出小张同学该天早餐刚好得到猪肉包和油饼的概率．‎ 解：解法一：树状图法 ‎∴小张同学得到猪肉包和油饼的概率为＝.‎ 解法二：列表法 猪肉包 面包 鸡蛋 油饼 猪肉包 猪肉包、面包 猪肉包、鸡蛋 猪肉包、油饼 面包 面包、猪肉包 面包、鸡蛋 面包、油饼 鸡蛋 鸡蛋、猪肉包 鸡蛋、面包 鸡蛋、油饼 油饼 油饼、猪肉包 油饼、面包 油饼、鸡蛋 ‎∴小张同学得到猪肉包和油饼的概率为＝.‎ ‎5．(2016·阜阳模拟)近几年“密室逃脱俱乐部”风靡全球，下图是俱乐部的通路俯视图，小明进行入口后，可任选一条通道过关．‎ ‎(1)他进A密室或B密室的可能性哪个大？请说明理由；(利用画树状图或列表法来求解)‎ ‎(2)求小明从中间通道进入A密室的概率．‎ 解：(1)根据题意，画树状图如下：‎ 由树状图可知，共有6种可能，小明进入A密室有2种可能，进入B密室有4种可能，‎ ‎∴小明进入A密室的概率P＝＝，‎ 小明进入B密室的概率P＝＝.‎ ‎∵<，∴他进B密室的可能性大．‎ ‎(2)由(1)中的树状图可知，小明从中间通道进入A密室只有一种可能，∴概率为.‎ ‎6．(2016·菏泽)锐锐参加我市电视台组织的“牡丹杯”智力竞答节目，答对最后两道单选题就顺利通关，第一道单选题有3个选项，第二道单选题有4个选项，这两道题锐锐都不会，不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项)．‎ ‎(1)如果锐锐两次“求助”都在第一道题中使用，那么锐锐通关的概率是；‎ ‎(2)如果锐锐两次“求助”都在第二道题中使用，那么锐锐通关的概率是．‎ ‎(3)如果锐锐将每道题各用一次“求助”，请用树状图或者列表来分析他顺序通关的概率．‎ 解：锐锐将每道题各用一次“求助”，分别用A，B表示剩下的第一道单选题的2个选项，a，b，c 表示剩下的第二道单选题的3个选项，树状图如图所示：‎ 共有6种等可能的结果，锐锐顺利通关的只有1种情况，‎ ‎∴锐锐顺利通关的概率为.‎ ‎7．(2015·淮北五校联考)某市某幼儿园六一期间举行亲子游戏，主持人请三位家长分别带自己的孩子参加游戏，主持人准备把家长和孩子重新组合完成游戏，A，B，C分别表示三位家长，他们的孩子分别对应的是a，b，c.‎ ‎(1)若主持人分别从三位家长和三位孩子中各选一人参加游戏，恰好是A，a的概率是多少？(直接写出答案)‎ ‎(2)若主持人先从三位家长中任选两人为一组，再从孩子中任选两人为一组，四人共同参加游戏，恰好是两对家庭成员的概率是多少．(画出树状图或列表)‎ 解：(1)P(恰好是A，a)≤.‎ ‎(2)依题意列表如下：‎ ‎　　‎ 家长　　‎ 孩子 ab ac bc AB AB，ab AB，ac AB，bc AC AC，ab AC，ac AC，bc BC BC，ab BC，ac BC，bc 共有9种情形，每种发生可能性相等，其中恰好是两对家庭成员有(AB，ab)，(AC，ac)，(BC，bc)3种，故恰好是两对家庭成员的概率P＝＝.‎ ‎ ‎