2017年河南省中考数学试卷(备用卷)打印版 5页

‎2017年河南省中考数学试卷（备用卷）‎ 一、选择题（每小题3分，共30分）下列各小题均有四个答案，其中只有一个是正确的，将正确答案的代号字母填入题后括号内 ‎1．下列各数中比小的数是　　‎ A． B． C． D．1‎ ‎2．今年端午节假期第一天，国内游客人数达3050万人次，将数据“3050万”用科学记数法表示为　　‎ A． B． C． D．‎ ‎3．下列不是正三棱柱的表面展开图的是　　‎ A． B． C． D．‎ ‎4．下列计算正确的是　　‎ A． B． C． D．‎ ‎5．不等式组的所有整数解的和是　　‎ A．3 B．2 C．2 D．0‎ ‎6．如图，在横格作业纸（横线等距）上画一条直线，与横格线交于，，三点，则等于　　‎ A． B． C． D．‎ ‎7．某市5月份连续7天的最高气温如下（单位：，30，34，36，36，33，37．这组数据的中位数、众数分别为　　‎ A．， B．， C．， D．，‎ ‎8．下列方程中没有实数根的是　　‎ A． B． C． D．‎ ‎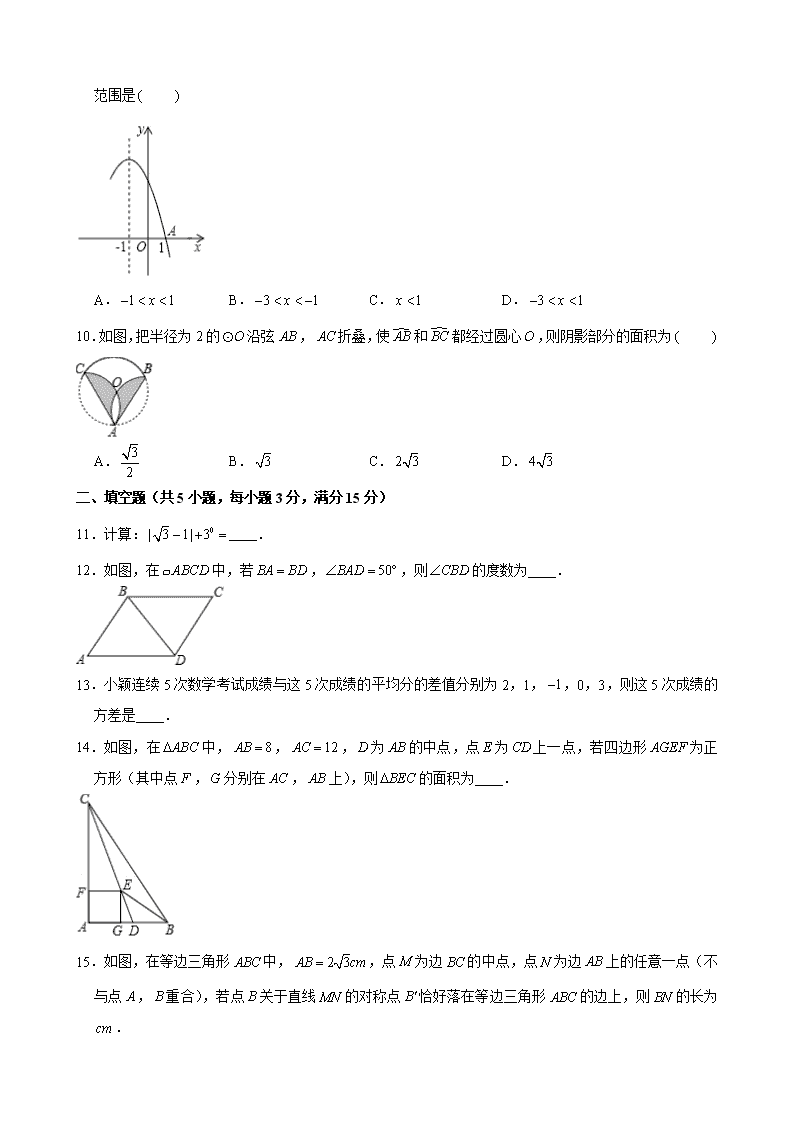9．如图，抛物线与轴交于点，对称轴为直线，当时，‎ 的取值范围是　　‎ A． B． C． D．‎ ‎10．如图，把半径为2的沿弦，折叠，使和都经过圆心，则阴影部分的面积为　　‎ A． B． C． D．‎ 二、填空题（共5小题，每小题3分，满分15分）‎ ‎11．计算：　　．‎ ‎12．如图，在中，若，，则的度数为　　．‎ ‎13．小颖连续5次数学考试成绩与这5次成绩的平均分的差值分别为2，1，，0，3，则这5次成绩的方差是　　．‎ ‎14．如图，在中，，，为的中点，点为上一点，若四边形为正方形（其中点，分别在，上），则的面积为　　．‎ ‎15．如图，在等边三角形中，，点为边的中点，点为边上的任意一点（不与点，重合），若点关于直线的对称点恰好落在等边三角形的边上，则的长为　　．‎ 三、解答题（本大题8个小题，共75分）‎ ‎16．先化简，再求值：，其中，．‎ ‎17．一个不透明的口袋中装有三个除所标数字外完全相同的小球， 小球上分别标有数字， 0 ， 1 ． 从袋中一次随机摸出两个小球， 把上面标注的两个数字分别作为点的横、 纵坐标 ．‎ ‎（1） 请用列表或画树状图的方法列出点所有可能的坐标；‎ ‎（2） 求点在直线上的概率 ．‎ ‎18．如图，为半圆的直径，点为半圆上任一点．‎ ‎（1）若，过点作半圆的切线交直线于点．求证：；‎ ‎（2）若，过点作的平行线交半圆于点．当以点，，，为顶点的四边形为菱形时，求的长．‎ ‎19．太阳能光伏发电因其清洁、安全、便利、高效等特点，已成为世界各国普遍关注和重点发展的新兴产业．如图是太阳能电池板支撑架的截面图，其中的粗线表示支撑角钢，太阳能电池板与支撑角钢的长度相同，均为，的倾斜角为，，支撑角钢，与底座地基台面接触点分别为、，垂直于地面，于点．两个底座地基高度相同（即点，到地面的垂直距离相同），均为，点到地面的垂直距离为，求支撑角钢和的长度各是多少（结果保留根号）．‎ ‎20．某服装专卖店计划购进，两种型号的精品女装．已知2件型女装和3件型女装共需5600元；1件型女装和2件型女装共需3400元．‎ ‎（1）求，型女装的单价 ‎（2）专卖店购进，两种型号的女装共60件，其中型的件数不少于型件数的2倍，如果型女装打八折，那么该专卖店至少需要准备多少贷款？‎ ‎21．如图，一次函数的图象与轴交于点，与反比例函数的图象交于点．以为对角线作矩形，使顶点，落在轴上（点在点的右边），与交于点．‎ ‎（1）求一次函数和反比例函数的解析式；‎ ‎（2）求点的坐标．‎ ‎22．如图，在等边三角形中，，点，分别是边，的中点，点，同时沿射线的方向以相同的速度运动，某一时刻分别运动到点，处，连接，，，．‎ ‎（1）写出图1中的一对全等三角形；‎ ‎（2）如图2所示，当点在线段延长线上时，画出示意图，判断（1）中所写的一对三角形是否仍然全等，并说明理由；‎ ‎（3）在点运动的过程中，若是直角三角形，直接写出此时线段的长度．‎ ‎23．如图1，在平面直角坐标系中，抛物线与直线交于点和点，与轴交于点．‎ ‎（1）求，的值及抛物线的解析式；‎ ‎（2）在图1中，把平移，始终保持点的对应点在抛物线上，点，的对应点分别为，‎ ‎，连接，若点恰好在直线上，求线段的长度；‎ ‎（3）如图2，在抛物线上是否存在点（不与点重合），使和的面积相等？若存在，直接写出点的坐标；若不存在，请说明理由．‎