中考数学压轴题重叠面积问题 22页

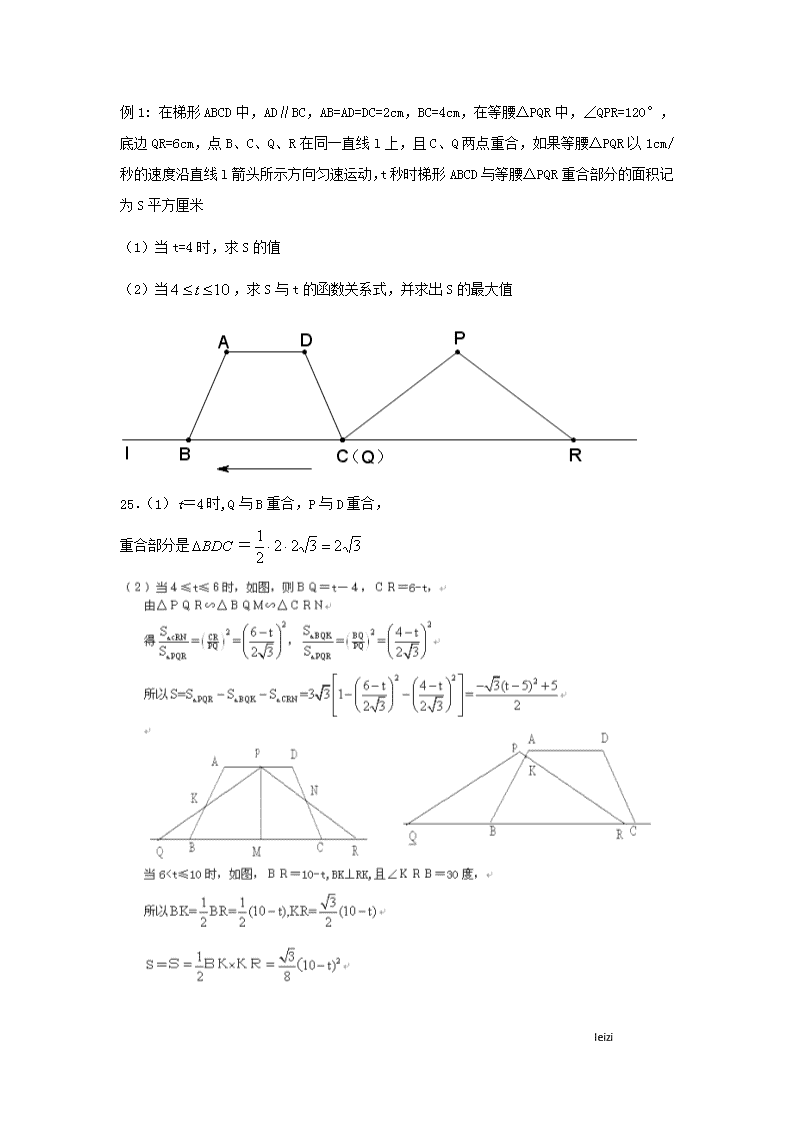
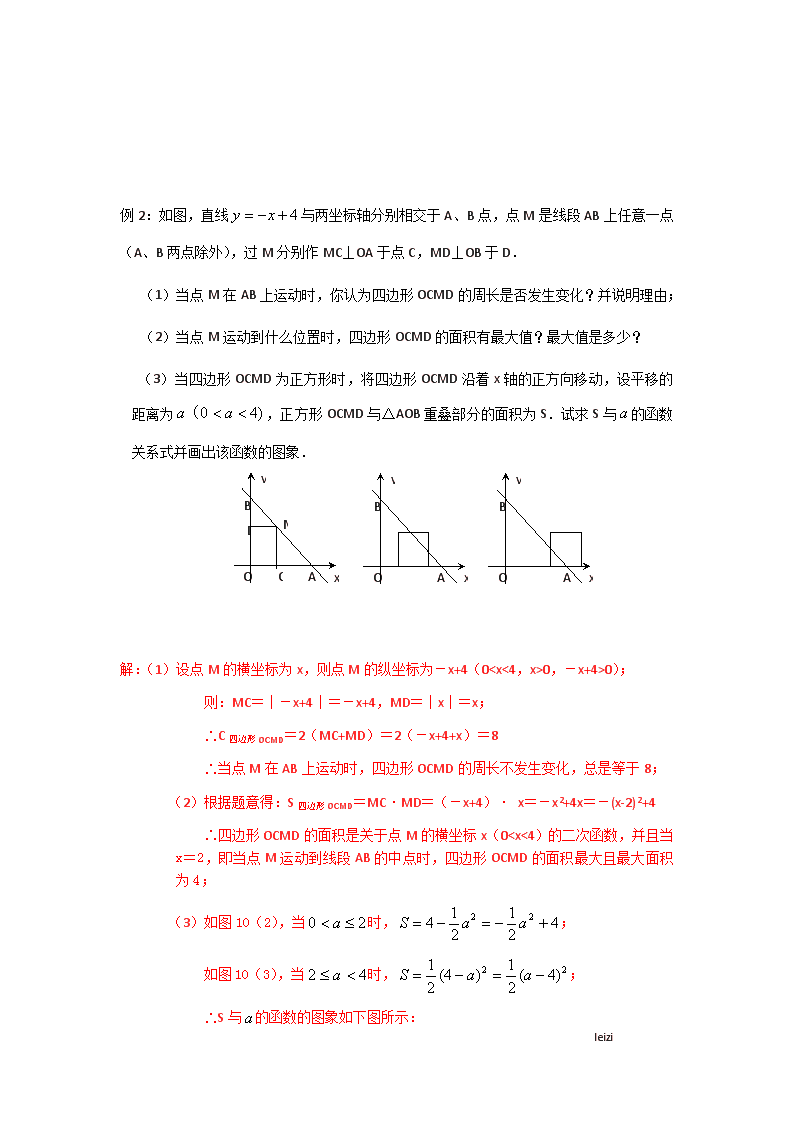
例1: 在梯形ABCD中，AD∥BC，AB=AD=DC=2cm，BC=4cm，在等腰△PQR中，∠QPR=120°，底边QR=6cm，点B、C、Q、R在同一直线l上，且C、Q两点重合，如果等腰△PQR以1cm/秒的速度沿直线l箭头所示方向匀速运动，t秒时梯形ABCD与等腰△PQR重合部分的面积记为S平方厘米 ‎（1）当t=4时，求S的值 ‎（2）当，求S与t的函数关系式，并求出S的最大值 ‎ ‎ ‎25．（1）t＝4时,Q与B重合，P与D重合，‎ 重合部分是＝‎ ‎ leizi 例2：如图，直线与两坐标轴分别相交于A、B点，点M是线段AB上任意一点（A、B两点除外），过M分别作MC⊥OA于点C，MD⊥OB于D．‎ ‎（1）当点M在AB上运动时，你认为四边形OCMD的周长是否发生变化？并说明理由；‎ ‎（2）当点M运动到什么位置时，四边形OCMD的面积有最大值？最大值是多少？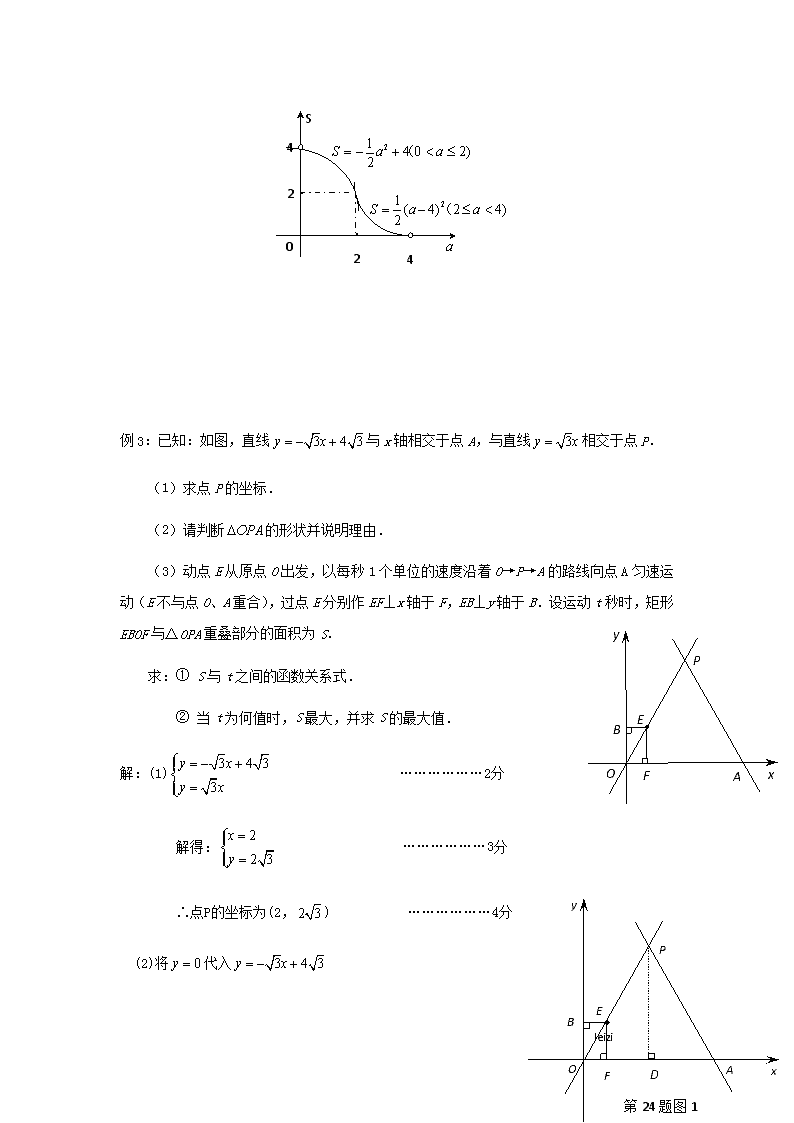‎ ‎（3）当四边形OCMD为正方形时，将四边形OCMD沿着x轴的正方向移动，设平移的距离为，正方形OCMD与△AOB重叠部分的面积为S．试求S与的函数关系式并画出该函B x y M C D O A B x y O A B x y O A 数的图象．‎ 解：（1）设点M的横坐标为x，则点M的纵坐标为－x+4（00，－x+4>0）；‎ ‎ 则：MC＝∣－x+4∣＝－x+4，MD＝∣x∣＝x；‎ ‎ ∴C四边形OCMD＝2（MC+MD）＝2（－x+4+x）＝8‎ ‎∴当点M在AB上运动时，四边形OCMD的周长不发生变化，总是等于8；‎ ‎（2）根据题意得：S四边形OCMD＝MC·MD＝（－x+4）· x＝－x2+4x＝－(x-2)2+4‎ ‎∴四边形OCMD的面积是关于点M的横坐标x（02，∴当t=时，S最大= ………………12分 例4: 已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示，四个顶点的坐标分别为O(0，0)，A(10，0)，B(8，)，C(0，)，点T在线段OA上(不与线段端点重合)，将纸片折叠，使点A落在射线AB上(记为点A′)，折痕经过点T，折痕TP与射线AB交于点P，设点T的横坐标为t，折叠后纸片重叠部分(图中的阴影部分)的面积为S；‎ ‎(1)求∠OAB的度数，并求当点A′在线段AB上时，S关于t的函数关系式；‎ ‎(2)当纸片重叠部分的图形是四边形时，求t的取值范围；‎ ‎(3)S存在最大值吗？若存在，求出这个最大值，并求此时t的值；若不存在，请说明理由。‎ 解：(1) ∵A，B两点的坐标分别是A(10，0)和B(8，)，‎ ‎ ∴，‎ ‎ ∴‎ ‎ 当点A´在线段AB上时，∵，TA=TA´，‎ ‎ ∴△A´TA是等边三角形，且，‎ ‎ ∴，，‎ ‎ leizi A´‎ y E ‎ ∴，‎ x O C T P B A ‎ 当A´与B重合时，AT=AB=，‎ ‎ 所以此时。‎ ‎ (2)当点A´在线段AB的延长线，且点P在线段AB(不与B重合)上时，‎ ‎ 纸片重叠部分的图形是四边形(如图(1)，其中E是TA´与CB的交点)，‎ A´‎ y x ‎ 当点P与B重合时，AT=2AB=8，点T的坐标是(2，0)‎ ‎ 又由(1)中求得当A´与B重合时，T的坐标是(6，0)‎ P B E ‎ 所以当纸片重叠部分的图形是四边形时，。‎ F C ‎ (3)S存在最大值 A T O ‎ 当时，，‎ ‎ 在对称轴t=10的左边，S的值随着t的增大而减小，‎ ‎∴当t=6时，S的值最大是。‎ 当时，由图，重叠部分的面积 ‎∵△A´EB的高是，‎ ‎∴‎ ‎ ‎ 当t=2时，S的值最大是；‎ 当，即当点A´和点P都在线段AB的延长线是(如图，其中E是TA´与CB的交点，F是TP与CB的交点)，‎ ‎∵，四边形ETAB是等腰形，∴EF=ET=AB=4，‎ ‎ leizi ‎∴‎ 综上所述，S的最大值是，此时t的值是。‎ 例6：如图，已知直线交坐标轴于两点，以线段为边向上作正方形，过点的抛物线与直线另一个交点为．‎ ‎（1）请直接写出点的坐标； ‎ ‎（2）求抛物线的解析式；‎ ‎（3）若正方形以每秒个单位长度的速度沿射线下滑，直至顶点落在轴上时停止．设正方形落在轴下方部分的面积为，求关于滑行时间的函数关系式，并写出相应自变量的取值范围；‎ ‎（4）在（3）的条件下，抛物线与正方形一起平移，同时停止，求抛物线上两点间的抛物线弧所扫过的面积．‎ 备用图 ‎（14分）（1）；…………………………………………………2分 ‎ （2）设抛物线为，抛物线过，‎ ‎ leizi ‎ 解得…………………………………………………2分 ‎∴．……………………………………………………………1分 ‎（3）①当点A运动到点F时，‎ 当时，如图1，‎ 图1‎ ‎ ∵， ‎ ‎∴∴‎ ‎∴；……2分 ‎ ②当点运动到轴上时，，‎ 图2‎ 当时，如图2， ‎ ‎∴∴，‎ ‎∵，‎ ‎∴‎ ‎ ‎ ‎ leizi ‎；…………（2分）‎ ‎ ‎ ‎③当点运动到轴上时，，‎ 当时，如图3，‎ 图3‎ ‎∵，‎ ‎∴，‎ ‎∵，‎ ‎∽‎ ‎∴，‎ ‎∴，‎ ‎∴ ‎ ‎ =．……（2分）‎ ‎（解法不同的按踩分点给分）‎ ‎（4）∵,,‎ ‎∴　………………………………………………（2分）‎ ‎ =‎ ‎ =．……………………………………………………………（1分）‎ ‎ leizi 图4‎ 例7:如图，已知直线与直线相交于点分别交轴 于两点．矩形的顶点分别在直线上，顶点都在轴上，且点与点重合．‎ ‎ （1）求的面积；‎ ‎（2）求矩形的边与的长；‎ ‎（3）若矩形从原点出发，沿轴的反方向以每秒1个单位长度的速度平移，设移动时间为秒，矩形与重叠部分的面积为，求关于的函数关系式，并写出相应的的取值范围．‎ ‎（1）解：由得点坐标为 由得点坐标为 ‎ leizi ‎∴ （2分）‎ 由解得∴点的坐标为 （3分）‎ ‎∴ （4分）‎ ‎ （2）解：∵点在上且 ‎ ∴点坐标为 （5分）‎ 又∵点在上且 ‎∴点坐标为 全 （6分）‎ ‎∴ （7分）‎ ‎ （3）解法一：当时，如图1，矩形与重叠部分为五边形（时，为四边形）．过作于，则 A D B E O R F x y y M ‎（图3）‎ G C A D B E O C F x y y G ‎（图1）‎ R M A D B E O C F x y y G ‎（图2）‎ R M ‎∴即∴‎ ‎∴‎ ‎ leizi 即 （10分）‎ ‎（2013•玉林压轴题）如图，抛物线y=﹣（x﹣1）2+c与x轴交于A，B（A，B分别在y轴的左右两侧）两点，与y轴的正半轴交于点C，顶点为D，已知A（﹣1，0）．‎ ‎（1）求点B，C的坐标；‎ ‎（2）判断△CDB的形状并说明理由；‎ ‎（3）将△COB沿x轴向右平移t个单位长度（0＜t＜3）得到△QPE．△QPE与△CDB重叠部分（如图中阴影部分）面积为S，求S与t的函数关系式，并写出自变量t的取值范围．‎ 解答：‎ 解：（1）∵点A（﹣1，0）在抛物线y=﹣（x﹣1）2+c上，‎ ‎∴0=﹣（﹣1﹣1）2+c，得c=4，‎ ‎∴抛物线解析式为：y=﹣（x﹣1）2+4，‎ 令x=0，得y=3，∴C（0，3）；‎ 令y=0，得x=﹣1或x=3，∴B（3，0）．‎ ‎（2）△CDB为直角三角形．理由如下：‎ 由抛物线解析式，得顶点D的坐标为（1，4）．‎ 如答图1所示，过点D作DM⊥x轴于点M，则OM=1，DM=4，BM=OB﹣OM=2．‎ 过点C作CN⊥DM于点N，则CN=1，DN=DM﹣MN=DM﹣OC=1．‎ 在Rt△OBC中，由勾股定理得：BC===；‎ ‎ leizi 在Rt△CND中，由勾股定理得：CD===；‎ 在Rt△BMD中，由勾股定理得：BD===．‎ ‎∵BC2+CD2=BD2，‎ ‎∴△CDB为直角三角形（勾股定理的逆定理）．‎ ‎（3）设直线BC的解析式为y=kx+b，∵B（3，0），C（0，3），‎ ‎∴，‎ 解得k=﹣1，b=3，‎ ‎∴y=﹣x+3，‎ 直线QE是直线BC向右平移t个单位得到，‎ ‎∴直线QE的解析式为：y=﹣（x﹣t）+3=﹣x+3+t；‎ 设直线BD的解析式为y=mx+m，∵B（3，0），D（1，4），‎ ‎∴，‎ 解得：m=﹣2，n=6，‎ ‎∴y=﹣2x+6．‎ 连接CQ并延长，射线CQ交BD于点G，则G（，3）．‎ 在△COB向右平移的过程中：‎ ‎（I）当0＜t≤时，如答图2所示：‎ 设PQ与BC交于点K，可得QK=CQ=t，PB=PK=3﹣t．‎ 设QE与BD的交点为F，则：，解得，∴F（3﹣t，2t）．‎ S=S△QPE﹣S△PBK﹣S△FBE=PE•PQ﹣PB•PK﹣BE•yF=×3×3﹣（3﹣t）2﹣t•2t=t2+3t；‎ ‎ leizi ‎（II）当＜t＜3时，如答图3所示：‎ 设PQ分别与BC、BD交于点K、点J．‎ ‎∵CQ=t，‎ ‎∴KQ=t，PK=PB=3﹣t．‎ 直线BD解析式为y=﹣2x+6，令x=t，得y=6﹣2t，‎ ‎∴J（t，6﹣2t）．‎ S=S△PBJ﹣S△PBK=PB•PJ﹣PB•PK=（3﹣t）（6﹣2t）﹣（3﹣t）2=t2﹣3t+．‎ 综上所述，S与t的函数关系式为：‎ S=．‎ ‎ leizi ‎（2013•鄂州压轴题）在平面直角坐标系中，已知M1（3，2），N1（5，﹣1），线段M1N1平移至线段MN处（注：M1与M，N1与N分别为对应点）．‎ ‎（1）若M（﹣2，5），请直接写出N点坐标．‎ ‎（2）在（1）问的条件下，点N在抛物线上，求该抛物线对应的函数解析式．‎ ‎（3）在（2）问条件下，若抛物线顶点为B，与y轴交于点A，点E为线段AB中点，点C（0，m）是y轴负半轴上一动点，线段EC与线段BO相交于F，且OC：OF=2：，求m的值．‎ ‎（4）在（3）问条件下，动点P从B点出发，沿x轴正方向匀速运动，点P运动到什么位置时（即BP长为多少），将△ABP沿边PE折叠，△APE与△PBE重叠部分的面积恰好为此时的△ABP面积的，求此时BP的长度．‎ 解答：‎ 解：（1）由于图形平移过程中，对应点的平移规律相同，‎ 由点M到点M′可知，点的横坐标减5，纵坐标加3，‎ 故点N′的坐标为（5﹣5，﹣1+3），即（0，2）．‎ N（0，2）；‎ ‎（2）∵N（0，2）在抛物线y=x2+x+k上 ‎ leizi ‎∴k=2‎ ‎∴抛物线的解析式为y=x2+x+2 ‎ ‎（3）∵y=x2+x+2=（x+2）2‎ ‎∴B（﹣2，0）、A（0，2）、E（﹣，1）‎ ‎∵CO：OF=2：‎ ‎∴CO=﹣m，FO=﹣m，BF=2+m ‎∵S△BEC=S△EBF+S△BFC=‎ ‎∴（2+m）（﹣m+1）=‎ 整理得：m2+m=0‎ ‎∴m=﹣1或0 ‎ ‎∵m＜0‎ ‎∴m=﹣1 ‎ ‎（4）在Rt△ABO中，tan∠ABO===‎ ‎∴∠ABO=30°，AB=2AO=4‎ ‎①当∠BPE＞∠APE时，连接A1B则对折后如图2，A1为对折后A的所落点，△EHP是重叠部分．‎ ‎∵E为AB中点，∴S△AEP=S△BEP=S△ABP ‎∵S△EHP=S△ABP ‎∴=S△EHP=S△BHP=S△ABP ‎∴A1H=HP，EH=HB=1‎ ‎∴四边形A1BPE为平行四边形 ‎ leizi ‎∴BP=A1E=AE=2‎ 即BP=2 ‎ ‎②当∠BPE=∠APE时，重叠部分面积为△ABP面积的一半，不符合题意；‎ ‎③当∠BPE＜∠APE时．‎ 则对折后如图3，A1为对折后A的所落点．△EHP是重叠部分 ‎∵E为AB中点，‎ ‎∴S△AEP=S△BEP=S△ABP ‎∵S△EHP=S△ABP∴S△EBH=S△EHP==S△ABP ‎∴BH=HP，EH=HA1=1‎ 又∵BE=EA=2‎ ‎∴EHAP，‎ ‎∴AP=2‎ 在△APB中，∠ABP=30°，AB=4，AP=2．[来源:学。科。网Z。X。X。K]‎ ‎∴∠APB=90°，‎ ‎∴BP=，‎ 综合①②③知：BP=2或；‎ ‎（2013浙江丽水12分）如图1，点A是轴正半轴上的动点，点B坐标为（0，4），M是线段AB的中点，将点M绕点A顺时针方向旋转90°得到点C，过点C作轴的垂线，垂足为F，过点B作轴的垂线与直线CF相交于点E，点D点A关于直线CF的对称点，连结AC，BC，CD，设点A的横坐标为 ‎（1）当时，求CF的长；‎ ‎（2）①当为何值时，点C落在线段BD上？‎ ‎②设△BCE的面积为S，求S与之间的函数关系式；‎ ‎（3）如图2，当点C与点E重合时，△CDF沿轴左右平移得到△C’D’‎ ‎ leizi ‎ F’，再将A，B，C’，D’为顶点的四边形沿C’F’剪开，得到两个图形，用这两个图形拼成不重叠且无缝隙的图形恰好是三角形，请直接写出所有符合上述条件的点C’的坐标。‎ ‎（2013浙江丽水12分）如图1，点A是轴正半轴上的动点，点B坐标为（0，4），M是线段AB的中点，将点M绕点A顺时针方向旋转90°得到点C，过点C作轴的垂线，垂足为F，过点B作轴的垂线与直线CF相交于点E，点D点A关于直线CF的对称点，连结AC，BC，CD，设点A的横坐标为 ‎（1）当时，求CF的长；‎ ‎（2）①当为何值时，点C落在线段BD上？‎ ‎②设△BCE的面积为S，求S与之间的函数关系式；‎ ‎（3）如图2，当点C与点E重合时，△CDF沿轴左右平移得到△C’D’ F’，再将A，B，C’，D’为顶点的四边形沿C’F’剪开，得到两个图形，用这两个图形拼成不重叠且无缝隙的图形恰好是三角形，请直接写出所有符合上述条件的点C’的坐标。‎ 解：（1）当时，OA=2，‎ ‎ ∵点B，∴OB=4．‎ ‎ 又∵，AB=2AC，可证RT∆ABO∽RT∆CAF．‎ ‎ leizi ‎ ∴，即．‎ ‎ （2）①当时，∵RT∆ABO∽RT∆CAF，‎ ‎ ∴，AF=2，‎ ‎ ∴FD=2，．‎ ‎ ∵点C落在线段BD上，∴RT∆CFD∽RT∆BOD，‎ ‎ ∴，整理得，‎ ‎ 解得：，（舍去）．‎ ‎ ∴当时，点C落在线段BD上．‎ ‎ ②当点C与点E重合时，CF=4，可得．‎ ‎ 当时，；‎ ‎ 当时，．‎ ‎ （3）点的坐标为：，，．‎ ‎ 理由如下：‎ ‎ ①如图1，当时，点的坐标为，‎ ‎ 根据≌，为拼成的三角形，此时的坐标为；‎ 图1‎ ‎ ‎ ‎ ②如图2，当点与点A重合时，点的坐标为，‎ ‎ leizi ‎ 根据≌，为拼成的三角形，此时的坐标为；‎ 图2‎ ‎ ‎ ‎ ③如图3，当时，点的坐标为，‎ ‎ 根据≌，为拼成的三角形，此时的坐标为；‎ 图3‎ ‎ ‎ ‎ leizi ‎ leizi ‎ leizi