中考数学几何题总汇 11页

‎1.三角形的有关概念 知识考点：‎ 理解三角形三边的关系及三角形的主要线段（中线、高线、角平分线）和三角形的内角和定理。关键是正确理解有关概念，学会概念和定理的运用。应用方程知识求解几何题是这部分知识常用的方法。‎ ‎【例1】已知一个三角形中两条边的长分别是、，且，那么这个三角形的周长的取值范围是（ ）‎ A、 B、‎ C、 D、‎ 变式与思考：在△ABC中，AC＝5，中线AD＝7，则AB边的取值范围是（ ）‎ A、1＜AB＜29 B、4＜AB＜24 ‎ C、5＜AB＜19 D、9＜AB＜19‎ ‎【例2】如图，已知△ABC中，∠ABC＝450，∠ACB＝610，延长BC至E，使CE＝AC，延长CB至D，使DB＝AB，求∠DAE的度数。‎ 一、填空题：‎ ‎1、三角形的三边为1，，9，则的取值范围是 。‎ ‎2、已知三角形两边的长分别为1和2，如果第三边的长也是整数，那么第三边的长为 。‎ ‎3、在△ABC中，若∠C＝2（∠A＋∠B），则∠C＝ 度。‎ ‎4、如果△ABC的一个外角等于1500，且∠B＝∠C，则∠A＝ 。‎ ‎5、如果△ABC中，∠ACB＝900，CD是AB边上的高，则与∠A相等的角是 。‎ ‎6、如图，在△ABC中，∠A＝800，∠ABC和∠ACB的外角平分线相交于点D，那么∠BDC＝ 。‎ ‎7、如图，CE平分∠ACB，且CE⊥DB，∠DAB＝∠DBA，AC＝‎18cm，△CBD的周长为‎28 cm，则DB＝ 。‎ ‎8、纸片△ABC中，∠A＝650，∠B＝750，将纸片的一角折叠，使点C落在△ABC内（如图），若∠1＝200，则∠2的度数为 。‎ ‎ ‎ 二、选择题：‎ ‎1、若△ABC的三边之长都是整数，周长小于10，则这样的三角形共有（ ）‎ A、6个 B、7个 C、8个 D、9个 ‎3、等腰三角形一腰上的中线分周长为15和12两部分，则此三角形底边之长为（ ）‎ A、7 B、‎11 C、7或11 D、不能确定 ‎2.全等三角形 知识考点：‎ 掌握用三角形全等的判定定理来解决有关的证明和计算问题，灵活运用三角形全等的三个判定定理来证明三角形全等。‎ 精典例题：‎ ‎【例1】如图，已知AB⊥BC，DC⊥BC，E在BC上，AE＝AD，AB＝BC。求证：CE＝CD。‎ 分析：作AF⊥CD的延长线（证明略）‎ 评注：寻求全等的条件，在证明两条线段（或两个角）相等时，若它们所在的两个三角形不全等，就必须添加辅助线，构造全等三角形，常见辅助线有：①连结某两个已知点；②过已知点作某已知直线的平行线；③延长某已知线段到某个点，或与已知直线相交；④作一角等于已知角。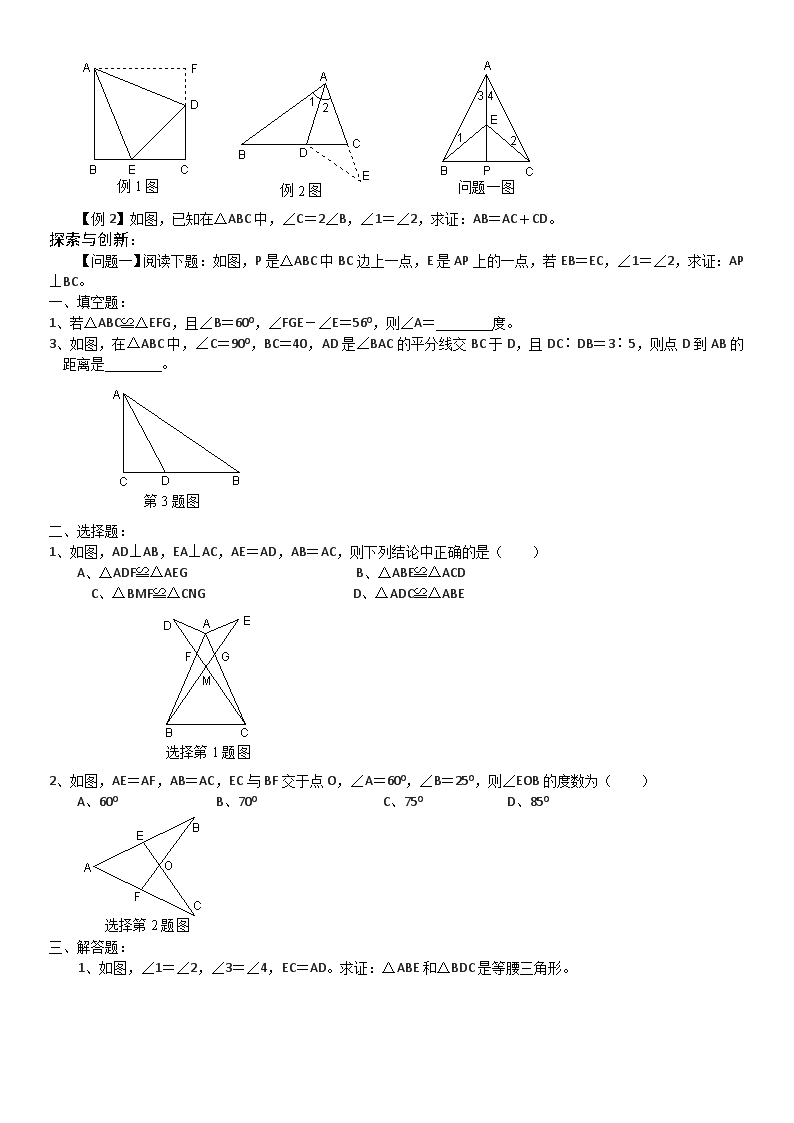‎ ‎ ‎ ‎【例2】如图，已知在△ABC中，∠C＝2∠B，∠1＝∠2，求证：AB＝AC＋CD。‎ 探索与创新：‎ ‎【问题一】阅读下题：如图，P是△ABC中BC边上一点，E是AP上的一点，若EB＝EC，∠1＝∠2，求证：AP⊥BC。‎ 一、填空题：‎ ‎1、若△ABC≌△EFG，且∠B＝600，∠FGE－∠E＝560，则∠A＝ 度。‎ ‎3、如图，在△ABC中，∠C＝900，BC＝40，AD是∠BAC的平分线交BC于D，且DC∶DB＝3∶5，则点D到AB的距离是 。‎ ‎ ‎ 二、选择题：‎ ‎1、如图，AD⊥AB，EA⊥AC，AE＝AD，AB＝AC，则下列结论中正确的是（ ）‎ ‎ A、△ADF≌△AEG B、△ABE≌△ACD C、△BMF≌△CNG D、△ADC≌△ABE ‎ ‎ ‎2、如图，AE＝AF，AB＝AC，EC与BF交于点O，∠A＝600，∠B＝250，则∠EOB的度数为（ ）‎ ‎ A、600 B、‎700 C、750 D、850‎ ‎ ‎ 三、解答题：‎ ‎1、如图，∠1＝∠2，∠3＝∠4，EC＝AD。求证：△ABE和△BDC是等腰三角形。‎ ‎ ‎ ‎2、如图，AB＝AE，∠ABC＝∠AED，BC＝ED，点F是CD的中点。‎ ‎（1）求证：AF⊥CD；‎ ‎（2）在你连结BE后，还能得出什么新结论？请再写出两个。‎ ‎3、（1）已知，在△ABC和△DEF中，AB＝DE，BC＝EF，∠BAC＝∠EDF＝1000，求证：△ABC≌△DEF；‎ ‎（2）上问中，若将条件改为AB＝DE，，BC＝EF，∠BAC＝∠EDF＝700，结论是否还成立，为什么？‎ ‎4、如图，已知∠MON的边OM上有两点A、B，边ON上有两点C、D，且AB＝CD，P为∠MON的平分线上一点。问：‎ ‎（1）△ABP与△PCD是否全等？请说明理由。‎ ‎（2）△ABP与△PCD的面积是否相等？请说明理由。‎ ‎ ‎ ‎4.直角三角形、勾股定理、面积 知识考点：‎ 了解直角三角形的判定与性质，理解直角三角形的边角关系，掌握用勾股定理解某些简单的实际问题。它的有关性质广泛应用于线段计算、证明线段倍分关系、证明线段平方关系及与面积有关的问题等方面。‎ 精典例题：‎ ‎【例1】如图，在四边形ABCD中，∠A＝600，∠B＝∠D＝900，BC＝2，CD＝3，则AB＝？‎ 分析：通过作辅助线，将四边形问题转化为三角形问题来解决，其关键是对内分割还是向外补形。‎ ‎ ‎ ‎【例2】如图，P为△ABC边BC上一点，PC＝2PB，已知∠ABC＝450，∠APC＝600，求∠ACB的度数。‎ ‎2、如图，D为△ABC的边BC上的一点，已知AB＝13，AD＝12，，BD＝5，AC＝BC，则BC＝ 。‎ ‎ ‎ ‎3、如图，四边形ABCD中，已知AB∶BC∶CD∶DA＝2∶2∶3∶1，且∠B＝900，则∠DAB＝ 。‎ ‎4、等腰△ABC中，一腰上的高为‎3cm，这条高与底边的夹角为300，则＝ 。‎ ‎5、如图，△ABC中，∠BAC＝900，∠B＝2∠C，D点在BC上，AD平分∠BAC，若AB＝1，则BD的长为 。‎ ‎6、已知Rt△ABC中，∠C＝900，AB边上的中线长为2，且AC＋BC＝6，则＝ 。‎ ‎7、如图，等腰梯形ABCD中，AD∥BC，腰长为‎8cm，AC、BD相交于O点，且∠AOD＝600，设E、F分别为CO、AB的中点，则EF＝ 。‎ ‎ ‎ ‎8、如图，点D、E是等边△ABC的BC、AC上的点，且CD＝AE，AD、BE相交于P点，BQ⊥AD。已知PE＝1，PQ＝3，则AD＝ 。‎ ‎9、如图所示，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为‎7cm，则正方形A、B、C、D的面积的和是 。‎ 二、选择题：‎ ‎3、在四边形ABCD中，AD⊥CD，AB＝13，BC＝12，CD＝4，AD＝3，则∠ACB的度数是（ ）‎ ‎ A、大于900 B、小于‎900 C、等于900 D、不能确定 ‎ ‎ ‎4、如图，已知△ABC中，∠B＝900，AB＝3，BC＝，OA＝OC＝，则∠OAB的度数为（ ）‎ ‎ A、100 B、‎150 C、200 D、250‎ ‎ 2、已知△ABC中，∠BAC＝750，∠C＝600，BC＝，求AB、AC的长。‎ ‎ ‎ ‎5.角平分线、垂直平分线 知识考点：‎ 了解角平分线、垂直平分线的有关性质和定理，并能解决一些实际问题。‎ 精典例题：‎ ‎【例题】如图，已知在△ABC中，AB＝AC，∠B＝300，AB的垂直平分线EF交AB于点E，交BC于点F，求证：‎ CF＝2BF。‎ ‎ ‎ ‎ ‎ ‎1、如图，∠A＝520，O是AB、AC的垂直平分线的交点，那么∠OCB＝ 。‎ ‎2、如图，已知AB＝AC，∠A＝440，AB的垂直平分线MN交AC于点D，则∠DBC＝ 。‎ ‎ ‎ ‎3、如图，在△ABC中，∠C＝900，∠B＝150，AB的中垂线DE交BC于D点，E为垂足，若BD＝8，则AC＝ 。‎ ‎4、如图，在△ABC中，AB＝AC，DE是AB的垂直平分线，△BCE的周长为24，BC＝10，则AB＝ 。‎ ‎4、如图，在Rt△ABC中，∠ACB＝900，AC＝BC，D为BC的中点，CE⊥AD，垂足为E，BF∥AC交CE的延长线于点F，求证AB垂直平分DF。‎ ‎6.平行四边形 知识考点：理解并掌握平行四边形的判定和性质 精典例题：‎ ‎【例1】已知如图：在四边形ABCD中，AB＝CD，AD＝BC，点E、F分别在BC和AD边上，AF＝CE，EF和对角线BD相交于点O，求证：点O是BD的中点。‎ ‎‎ ‎ 【例2】已知如图：在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA边上的中点，求证：四边形EFGH是平行四边形。‎ 分析：欲证四边形EFGH是平行四边形，根据条件需从边上着手分析，由E、F、G、H分别是各边上的中点，可联想到三角形的中位线定理，连结AC后，EF和GH的关系就明确了，此题也便得证。（证明略）‎ 变式1：顺次连结矩形四边中点所得的四边形是菱形。‎ 变式2：顺次连结菱形四边中点所得的四边形是矩形。‎ 变式3：顺次连结正方形四边中点所得的四边形是正方形。‎ 变式4：顺次连结等腰梯形四边中点所得的四边形是菱形。‎ 变式5：若AC＝BD，AC⊥BD，则四边形EFGH是正方形。‎ 变式6：在四边形ABCD中，若AB＝CD，E、F、G、H分别为AD、BC、BD、AC的中点，求证：EFGH是菱形。‎ ‎ ‎ 跟踪训练：‎ 一、填空题：‎ ‎1、一个平行四边形的两条对角线的长度分别为5和7，则它的一条边长的取值范围是 。‎ ‎2、□ABCD的周长是30，AC、BD相交于点O，△OAB的周长比△OBC的周长大3，则AB＝ 。‎ ‎3、已知□ABCD中，AB＝2AD，对角线BD⊥AD，则∠BCD的度数是 。‎ ‎4、如图：在□ABCD中，AE⊥BD于E，∠EAD＝600，AE＝2，AC＋BD＝16，则△BOC的周长为 。‎ ‎ ‎ ‎5、如图：□ABCD的对角线AC、BD相交于O，EF过点O，且EF⊥BC于F，∠1＝300，∠2＝450，OD＝，则AC的长为 。‎ ‎6、如图：过□ABCD的顶点B作高BE、BF，已知BF＝BE，BC＝16，∠EBF＝300，则AB＝ 。‎ ‎7、如图所示，□ABCD的周长为30，AE⊥BC于点E，AF⊥CD于点F，且AE∶AF＝2∶3，∠C＝1200，则平行四边形ABCD的面积为 。‎ 二、选择题：‎ ‎1、若□ABCD的周长为28，△ABC的周长为‎17cm，则AC的长为（ ）‎ A、‎11cm B、‎5.5cm C、‎4cm D、‎‎3cm ‎ ‎ ‎4、如图，在△ABC中，∠ACB＝900，D、F分别为AC、AB的中点，点E在BC的延长线上，∠CDE＝∠A。‎ ‎（1）求证：四边形DECF是平行四边形；‎ ‎（2）若，四边形EBFD的周长为22，求DE的长。‎ ‎7.矩形、菱形 知识考点：理解并掌握矩形的判定与性质，并能利用所学知识解决有关问题。‎ 精典例题：‎ ‎【例1】如图，已知矩形ABCD中，对角线AC、BD相交于点O，AE⊥BD，垂足为E，∠DAE∶∠BAE＝3∶1，求∠EAC的度数。‎ ‎ ‎ ‎【例2】如图，已知菱形ABCD的边长为3，延长AB到点E，使BE＝2AB，连结EC并延长交AD的延长线于点F，求AF的长。‎ ‎1、若矩形的对称中心到两边的距离差为4，周长为56，则这个矩形的面积为 。‎ ‎2、已知菱形的锐角是600，边长是‎20cm，则较短的对角线长是 cm。‎ ‎3、如图，矩形ABCD中，O是对角线的交点，若AE⊥BD于E，且OE∶OD＝1∶2，AE＝cm，则DE＝ cm。‎ ‎ ‎ 二、选择题：‎ ‎ ‎ ‎8、如图，已知矩形纸片ABCD中，AD＝‎9cm，AB＝‎3cm，将其折叠，使点D与点B重合，那么折叠后DE的长和折痕EF的长分别是（ ）‎ ‎ A、‎4cm、cm B、‎5cm、cm ‎ C、‎4cm、cm D、‎5cm、cm ‎10、平行四边形四个内角的平分线，如果能围成一个四边形，那么这个四边形一定是（ ）‎ ‎ A、矩形 B、菱形 C、正方形 D、等腰梯形 三、解答题：‎ ‎ 、‎ ‎12、如图，在△ABC中，∠ACB＝900，CD是AB边上的高，∠BAC的平分线AE交CD于F，EG⊥AB于G，求证：四边形GECF是菱形。‎ ‎8.正方形 ‎ ‎ ‎【例2】如图，在正方形ABCD中，P、Q分别是BC、CD上的点，若∠PAQ＝450，求证：PB＋DQ＝PQ。‎ ‎9.梯形 知识考点：‎ 掌握梯形、直角梯形、等腰梯形的判定和性质，并能熟练解决实际问题。‎ 精典例题：‎ ‎【例1】如图，在梯形ABCD中，AB∥DC，中位线EF＝7，对角线AC⊥BD，∠BDC＝300，求梯形的高AH。‎ ‎ ‎ ‎【例2】如图，梯形ABCD中，AD∥BC，E、F分别是AD、BC的中点，∠B＋∠C＝900，AD＝7，BC＝15，求EF的长。‎ 一、填空题：‎ ‎1、梯形的上底长为3，下底长为7，梯形的中位线所分成的上下两部分的面积之比为 。‎ ‎2、等腰梯形中，上底∶腰∶下底＝1∶2∶3，则下底角的度数是 。‎ ‎3、如图，直角梯形ABCD中，AD∥BC，CD＝10，∠C＝600，则AB的长为 。‎ ‎ ‎ ‎6、如图，在等腰梯形ABCD中，AD∥BC，AB＝DC，CD＝BC，E是BA、CD延长线的交点，∠E＝400，则∠ACD＝ 度。‎ 二、选择题：‎ ‎ ‎ ‎3、已知如图，梯形ABCD中，AD∥BC，∠B＝450，∠C＝1200，AB＝8，则CD的长为（ ）‎ ‎ A、 B、 C、 D、‎ ‎4、如图，在直角梯形ABCD中，底AB＝13，CD＝8，AD⊥AB，并且AD＝12，则A到BC的距离为（ ）‎ A、12 B、‎13 C、10 D、12×21＋13‎ 三、解答题：‎ ‎1、如图，梯形ABCD中，AD∥BC，AB＝DC，在AB、DC上各取一点F、G，使BF＝CG，E是AD的中点。求证：∠EFG＝∠EGF。‎ ‎ ‎ ‎11.锐角三角函数 ‎【例1】在Rt△ABC中，∠C＝900，AC＝12，BC＝15。‎ ‎（1）求AB的长；‎ ‎（2）求sinA、cosA的值；‎ ‎（3）求的值；‎ ‎（4）比较sinA、cosB的大小。‎ ‎【例3】已知，在Rt△ABC中，∠C＝900，，那么cosA（ ）‎ A、 B、 C、 D、‎ ‎1、在Rt△ABC中，∠C＝900，若，则sinA＝（ ）‎ A、 B、 C、 D、‎ ‎ A、200 B、‎300 C、400 D、500‎ ‎5、在Rt△ABC中，∠C＝900，，AC＝6，则BC的长为（ ）‎ ‎ A、6 B、‎5 C、4 D、2‎ ‎6、某人沿倾斜角为的斜坡前进‎100米，则他上升的最大高度为（ ）‎ A、米 B、米 C、米 D、米 ‎13. 三角函数的综合运用 知识考点：‎ 本课时主要是解直角三角形的应用，涉及到的内容包括航空、航海、工程、测量等领域。要求能灵活地运用解直角三角形的有关知识，解决这些实际问题。熟悉仰角、俯角、坡度、方位角等概念，常用的方法是通过数形结合、建立解直角三角形的数学模型。‎ 精典例题：‎ ‎【例1】如图，塔AB和楼CD的水平距离为‎80米，从楼顶C处及楼底D处测得塔顶A的仰角分别为450和600，试求塔高与楼高（精确到‎0.01米）。‎ ‎（参考数据：＝1.41421…，＝1.73205…）‎ ‎【例1】如图，在△ABC中，AB＝‎14cm，，DE∥BC，CD⊥AB，CD＝‎12cm，求△ADE的面积和周长。‎ ‎ ‎ ‎【例2】如图，正方形DEMF内接于△ABC，若，，求 ‎19.圆的有关概念和性质 知识考点：‎ ‎1、理解圆的定义，掌握点与圆的位置关系；‎ ‎2、理解弦、弧、半圆、优弧、同心圆、等圆、等弧、弓形、圆心角、圆周角等与圆有关的概念；‎ ‎3、掌握圆心角、弧、弦、弦心距之间的关系，并会运用这些关系解决一些几何证明题和计算题。‎ 精典例题：‎ ‎【例1】在平面直角坐标系内，以原点O为圆心，5为半径作⊙O，已知A、B、C三点的坐标分别为A（3，4），B（－3，－3），C（4，）。试判断A、B、C三点与⊙O的位置关系。‎ ‎3、三角形的外心恰在它的一条边上，那么这个三角形是（ ）‎ A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定 ‎【例3】如图，等腰△ABC内接于半径为‎5cm的⊙O，AB＝AC，tanB＝。求：‎ ‎（1）BC的长；‎ ‎（2）AB边上高的长。‎ ‎4、若圆中一弦与弦高之和等于直径，弦高长为1，则圆的半径长为（ ）‎ ‎ A、1 B、 C、2 D、‎ 二、填空题：‎ ‎3、等腰△ABC中，AB＝AC，∠A＝1200，BC＝‎10 cm，则△ABC的外接圆半径为 。‎ ‎4、圆内一弦与直径相交成300的角，且分直径为‎1 cm和‎5 cm两段，则此弦长为 。‎ ‎ ‎ 三、计算或证明题：‎ ‎1、如图，Rt△ABC中，∠C＝900，AC＝3，BC＝4，以点C为圆心，CA为半径的圆与AB、BC分别交于点D、E，求AB、AD的长。‎ ‎ ‎ ‎1、如图，PA切⊙O于A，PB＝4，PO＝5，则PA＝ 。‎ ‎ ‎