2014年广东省中考数学试题含答案 10页

‎2014年广东数学中考试卷 一、选择题（本大题10小题，每小题3分，共30分）‎ ‎1、在1，0，2，-3这四个数中，最大的数是（ ）‎ ‎ A、1 B、0 C、2 D、-3‎ ‎2、在下列交通标志中，既是轴对称图形，又是中心对称图形的是（ ）‎ ‎ ‎ ‎ A、 B、 C、 D、‎ ‎3、计算3a-2a的结果正确的是（ ）‎ A、1 B、a C、-a D、-5a ‎4、把分解因式，结果正确的是（ ）‎ ‎ A、 B、 C、 D、‎ ‎5、一个多边形的内角和是900°，这个多边形的边数是（ ）‎ ‎ A、10 B、9 C、8 D、7‎ ‎6、一个不透明的布袋里装有7个只有颜色不同的球，其中3个红球，4个白球，从布袋中随机摸出一个球，摸出的球是红球的概率是（ ）‎ ‎ A、 B、 C、 D、‎ ‎7、如图7图，□ABCD中，下列说法一定正确的是（ ） ‎ A、AC=BD B、AC⊥BD C、AB=CD D、AB=BC 题7图 ‎8、关于x的一元二次方程有两个不相等的实数根，则实数m的取值范围为（ ）‎ A、 B、 C、 D、‎ ‎9、一个等腰三角形的两边长分别是3和7，则它的周长为（ ）‎ A、17 B、15 C、13 D、13或17‎ ‎10、二次函数的大致图象如题10图所示，‎ 题10图 关于该二次函数，下列说法错误的是（ ）‎ A、函数有最小值 B、对称轴是直线x=‎ C、当x<,y随x的增大而减小 D、当 -1 < x < 2时，y>0 ‎ 二、填空题（本大题6小题，每小题4分，共24分）‎ ‎11、计算= ；‎ ‎12、据报道，截止2013年12月我国网民规模达618 000 000人.将618 000 000用科学计数法表示为 ；‎ ‎13、如题13图，在△ABC中，点D，E分别是AB，AC的中点，若BC=6，则DE= ；‎ ‎ 题13图 题14图 ‎14、如题14图，在⊙O中，已知半径为5，弦AB的长为8，‎ 那么圆心O 到AB的距离为 ；‎ ‎15、不等式组的解集是 ；‎ ‎16、如题16图，△ABC绕点A顺时针旋转45°‎ 得到△，若∠BAC=90°，AB=AC=， 题16图 则图中阴影部分的面积等于 。 ‎ 三、解答题（一）（本大题3小题，每小题6分，共18分）‎ ‎17、计算：‎ ‎18、先化简，再求值：，其中 ‎19、如题19图，点D在△ABC的AB边上，且∠ACD=∠A.‎ ‎ （1）作△BDC的平分线DE，交BC于点E ‎（用尺规作图法，保留作图痕迹，不要求写作法）；‎ ‎ （2）在（1）的条件下，判断直线DE与直线 AC的位置关系（不要求证明）. 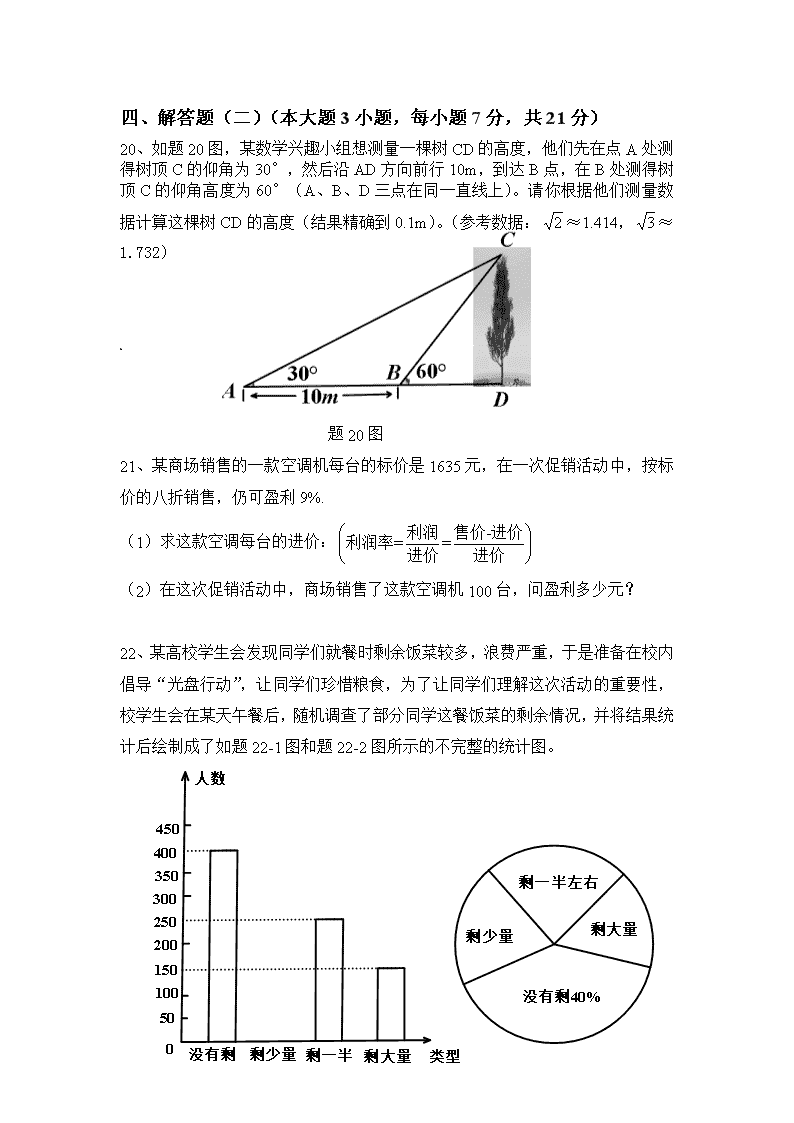‎ ‎ 题19图 四、解答题（二）（本大题3小题，每小题7分，共21分）‎ ‎20、如题20图，某数学兴趣小组想测量一棵树CD的高度，他们先在点A处测得树顶C的仰角为30°，然后沿AD方向前行10m，到达B点，在B处测得树顶C的仰角高度为60°（A、B、D三点在同一直线上）。请你根据他们测量数据计算这棵树CD的高度（结果精确到0.1m）。（参考数据：≈1.414，≈1.732）‎ ‎ 题20图 ‎21、某商场销售的一款空调机每台的标价是1635元，在一次促销活动中，按标价的八折销售，仍可盈利9%.‎ ‎（1）求这款空调每台的进价：‎ ‎（2）在这次促销活动中，商场销售了这款空调机100台，问盈利多少元？‎ ‎22、某高校学生会发现同学们就餐时剩余饭菜较多，浪费严重，于是准备在校内倡导“光盘行动”，让同学们珍惜粮食，为了让同学们理解这次活动的重要性，校学生会在某天午餐后，随机调查了部分同学这餐饭菜的剩余情况，并将结果统计后绘制成了如题22-1图和题22-2图所示的不完整的统计图。 ‎ （1） 这次被调查的同学共有 名；‎ （2） 把条形统计图（题22-1图）补充完整；‎ （3） 校学生会通过数据分析，估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐。据此估算，该校18 000名学生一餐浪费的食物可供多少人食用一餐？‎ 五、解答题（三）（本大题3小题，每小题9分，共27分）‎ ‎23、如题23图，已知A，B（-1,2）是一次函数与反比例函数 ‎（）图象的两个交点，AC⊥x轴于C，BD⊥y轴于D。‎ （1） 根据图象直接回答：在第二象限内，当x取何值时，一次函数大于反比例函数的值?‎ （2） 求一次函数解析式及m的值；‎ （3） P是线段AB上的一点，连接PC，PD，若△PCA和△PDB面积相等，求点P坐标。‎ ‎ ‎ ‎ 题23图 题24图 ‎24、如题24图，⊙是△ABC的外接圆，AC是直径，过点O作OD⊥AB于点D，延长DO交⊙于点P，过点P作PE⊥AC于点E，作射线DE交BC的延长线于F点，连接PF。‎ ‎（1）若∠POC=60°，AC=12，求劣弧PC的长；（结果保留π）‎ ‎（2）求证：OD=OE；‎ ‎（3）PF是⊙的切线。‎ ‎25、如题25-1图，在△ABC中，AB=AC，AD⊥AB点D，BC=10cm，AD=8cm，点P从点B出发，在线段BC上以每秒3cm的速度向点C匀速运动，与此同时，垂直于AD的直线m从底边BC出发，以每秒2cm的速度沿DA方向匀速平移，分别交AB、AC、AD于E、F、H，当点P到达点C时，点P与直线m同时停止运动，设运动时间为t秒（t＞0）。‎ ‎（1）当t=2时，连接DE、DF，求证：四边形AEDF为菱形；‎ ‎（2）在整个运动过程中，所形成的△PEF的面积存在最大值，当△PEF的面积最大时，求线段BP的长；‎ ‎（3）是否存在某一时刻t，使△PEF为直角三角形？若存在，请求出此时刻t的值，若不存在，请说明理由。‎ ‎ 题25-1图 题25备用图 参考答案：‎ 一、 选择题：‎ ‎1~10：CCBDD BCBAD 二、填空题:‎ ‎11、 12、 13、3 14、3‎ ‎15、 16、‎ 三、解答题（一）‎ ‎ 17、6 18、； 19、(1)图略；(2)平行 四、解答题（二）‎ ‎20、解：由题意可知：CD⊥AD，设CD=x m 在Rt△BCD中，‎ 在Rt△ACD中，‎ 又∵AD=AB＋BD，∴‎ 解得：‎ ‎21、(1)1200； (2)10800‎ ‎22、（1）1000； （2）如图； ‎ ‎（3）3600 ‎ 五、解答题（三）‎ ‎23、解：（1）由图象，当时，一次函数值大于反比例函数的值。‎ ‎ （2）把A，B（－1，2）代入得，‎ P ‎ ，解得 ‎ ∴ 一次函数的解析式为 ‎ 把B（－1，2）代入得，即m的值为－2。‎ ‎ （3）如图，设P的坐标为（，），由A、B的坐标可知AC=，OC=4，BD=1，OD=2，‎ ‎ 易知△PCA的高为，△PDB的高，由可得 ‎ ，解得，此时 ‎ ∴ P点坐标为（，）‎ ‎24、（1）解：由直径AC=12得半径OC=6‎ 劣弧PC的长为 ‎（2）证明：∵ OD⊥AB，PE⊥AC ‎ ∴ ∠ADO=∠PEO=90°‎ ‎ 在△ADO和△PEO中，‎ ‎ ‎ ‎ ∴ △ADO≌△PEO ‎∴ OD=OE ‎（3）解：连接PC，由AC是直径知BC⊥AB，又OD⊥AB，‎ ‎ ∴ PD∥BF ‎ ∴ ∠OPC=∠PCF，∠ODE=∠CFE ‎ 由（2）知OD=OE，则∠ODE=∠OED，又∠OED=∠FEC ‎ ∴ ∠FEC=∠CFE ‎ ∴ EC=FC ‎ 由OP=OC知∠OPC=∠OCE ‎ ∴ ∠PCE =∠PCF ‎ 在△PCE和△PFC中，‎ ‎ ∴ △PCE≌△PFC ‎ ∴ ∠PFC =∠PEC=90°‎ ‎ 由∠PDB=∠B=90°可知∠ODF=90°即OP⊥PF ‎ ∴ PF是⊙的切线 ‎25、解：（1）当t=2时，DH=AH=4，由AD⊥AB，AD⊥EF可知EF∥BC ‎ ∴ ，‎ ‎ 又∵ AB=AC，AD⊥BC ‎ ∴ BD=CD ‎ ∴ EH=FH ‎ ∴ EF与AD互相垂直平分 ‎ ∴ 四边形AEDF为菱形 ‎ （2）依题意得DH=2t，AH=8－2t，BC=10cm，AD=8cm，由EF∥BC知△AEF∽△ABC ‎ ∴ 即，解得 ‎ ∴ ‎ ‎ 即△PEF的面积存在最大值10cm2，此时BP=3×2=6cm。‎ ‎ （3）过E、F分别作EN⊥BC于N，EM⊥BC于M，易知EF=MN=‎ ‎ EN=FM，由AB=AC可知BN=CM=‎ ‎ 在和中，由， 即，‎ 解得，又由知，‎ ‎，‎ ‎ 则 ， ‎ ‎ ‎ 分三种情况讨论：‎ ‎ ①若∠EPF=90°，则，解得，（舍去）‎ ‎②若∠EFP=90°，则，解得，（舍去）‎ 图25-1‎ 第25题备用图 E F N M D P ‎③若∠FEP=90°，则，解得，（均舍去）‎ 综上所述，当或时，△PEF为直角三角形。‎