上海中考几何专题训练 5页

‎2015年上海中考几何专题训练 ‎1．（本题满分12分，每小题满分各6分)‎ A B C E D F 图8‎ 如图8，已知△和△都是等边三角形，点在边上，点在边的右侧，联结．‎ ‎（1）求证：；‎ ‎（2）在边上取一点，使，联结、．‎ 求证：四边形是等腰梯形．‎ ‎2．（本题满分12分，其中每小题各6分）‎ 如图，已知在梯形ABCD中，AD // BC ，∠A = 90º，AB = AD．点E在边AB上，且DE⊥CD，DF平分∠EDC，交BC于点F，联结CE、EF．‎ ‎（1）求证：DE = DC；‎ ‎（第23题图）‎ A B C D E F ‎（2）如果，求证：∠BEF =∠CEF．‎ ‎3．（本题满分12分）‎ 第23题图 ‎ 如图，正方形ABCD中，点E、F分别在边BC、CD上，AE=AF，AC和EF交于点O，延长AC至点G，使得AO=OG，联结EG、FG.‎ ‎ （1）求证: BE=DF；‎ ‎ （2）求证:四边形AEGF是菱形.‎ ‎4.（本题满分12分，每小题各6分）‎ A ‎（第23题图）‎ E G D F C B 如图，已知在正方形ABCD中，点E在CD边上，过C点作AE的垂线交于点F，联结DF，过点D作DF的垂线交AF于点G，联结BG.‎ ‎（1）求证：△ADG≌△CDF；‎ ‎（2）如果E为CD的中点，求证：BG⊥AF.‎ ‎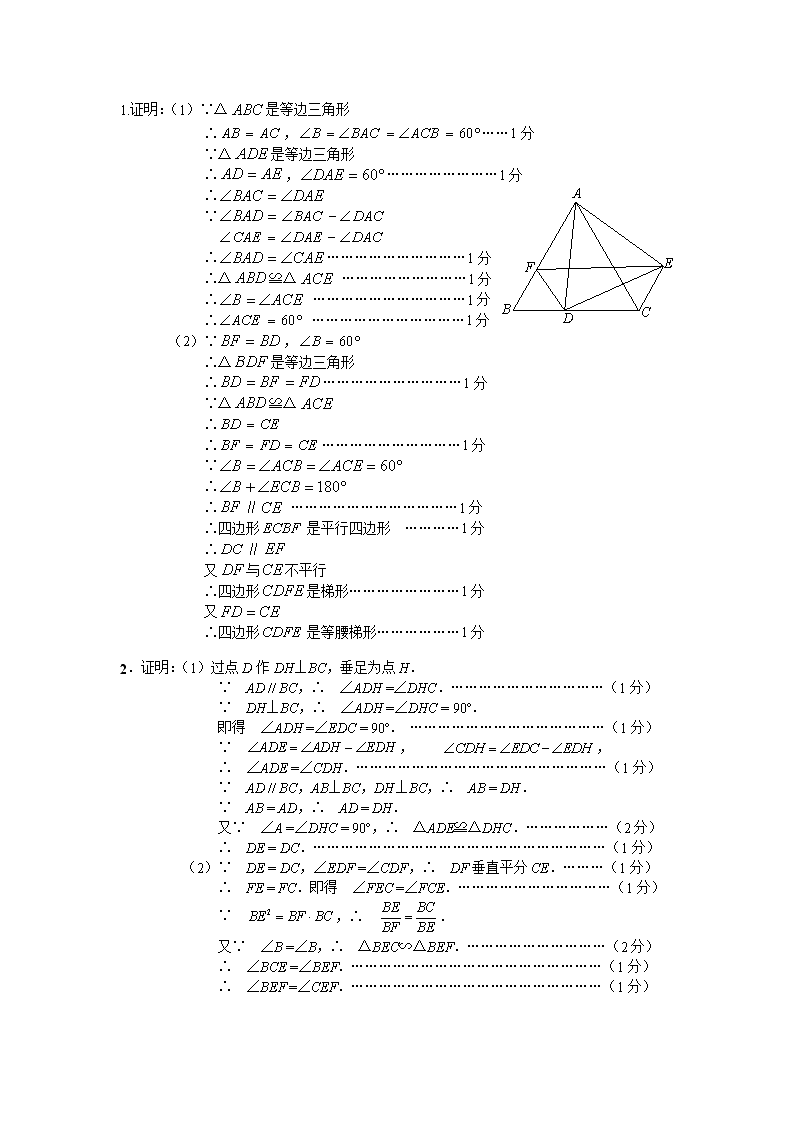1.证明：（1）∵△是等边三角形 ‎∴，……1分 ‎∵△是等边三角形 A B C E D F ‎∴，……………………1分 ‎∴‎ ‎∵‎ ‎∴…………………………1分 ‎∴△≌△ ………………………1分 ‎∴ ……………………………1分 ‎∴ ……………………………1分 ‎（2）∵，‎ ‎ ∴△是等边三角形 ‎ ∴…………………………1分 ‎∵△≌△‎ ‎ ∴‎ ‎∴…………………………1分 ‎∵‎ ‎∴‎ ‎∴∥ ………………………………1分 ‎∴四边形是平行四边形 …………1分 ‎∴∥‎ 又与不平行 ‎∴四边形是梯形……………………1分 又 ‎∴四边形是等腰梯形………………1分 ‎2．证明：（1）过点D作DH⊥BC，垂足为点H．‎ ‎∵ AD // BC，∴ ∠ADH =∠DHC．……………………………（1分）‎ ‎∵ DH⊥BC，∴ ∠ADH =∠DHC = 90º． ‎ 即得 ∠ADH =∠EDC = 90º． ……………………………………（1分）‎ ‎∵ ， ，‎ ‎∴ ∠ADE =∠CDH．………………………………………………（1分）‎ ‎∵ AD // BC，AB⊥BC，DH⊥BC，∴ AB = DH．‎ ‎∵ AB = AD，∴ AD = DH．‎ 又∵ ∠A =∠DHC = 90º，∴ △ADE≌△DHC．………………（2分）‎ ‎∴ DE = DC．………………………………………………………（1分）‎ ‎（2）∵ DE = DC，∠EDF =∠CDF，∴ DF垂直平分CE．………（1分）‎ ‎∴ FE = FC．即得 ∠FEC =∠FCE．……………………………（1分）‎ ‎∵ ，∴ ．‎ 又∵ ∠B =∠B，∴ △BEC∽△BEF．…………………………（2分）‎ ‎∴ ∠BCE =∠BEF．………………………………………………（1分）‎ ‎∴ ∠BEF =∠CEF．………………………………………………（1分）‎ ‎3．（本题满分12分）‎ 证：（1）∵正方形ABCD ∴AB=AD ∠B=∠D=90°‎ 第23题图 ‎ 在Rt△ABD和Rt△ACD中 ‎ ‎∴△ABE≌△ADF ‎ ‎∴BE=DF. （5分）‎ ‎（2）∵正方形ABCD ∴BC=CD ‎∵ BE=DF ∴CE=CF ‎ ‎ ∴△ECF是等腰三角形 ‎∵正方形ABCD ∴AC平分∠BCD ‎ ∴AC⊥EF 且EO=OF ‎ ∵AO=OG ‎∴四边形AEGF是平行四边形（5分）‎ ‎ ∵AC⊥EF ‎ ‎ ∴四边形AEGF是菱形. （2分）‎ ‎4‎ ‎5‎ ‎5‎