中考数学旋转模型及例题 3页

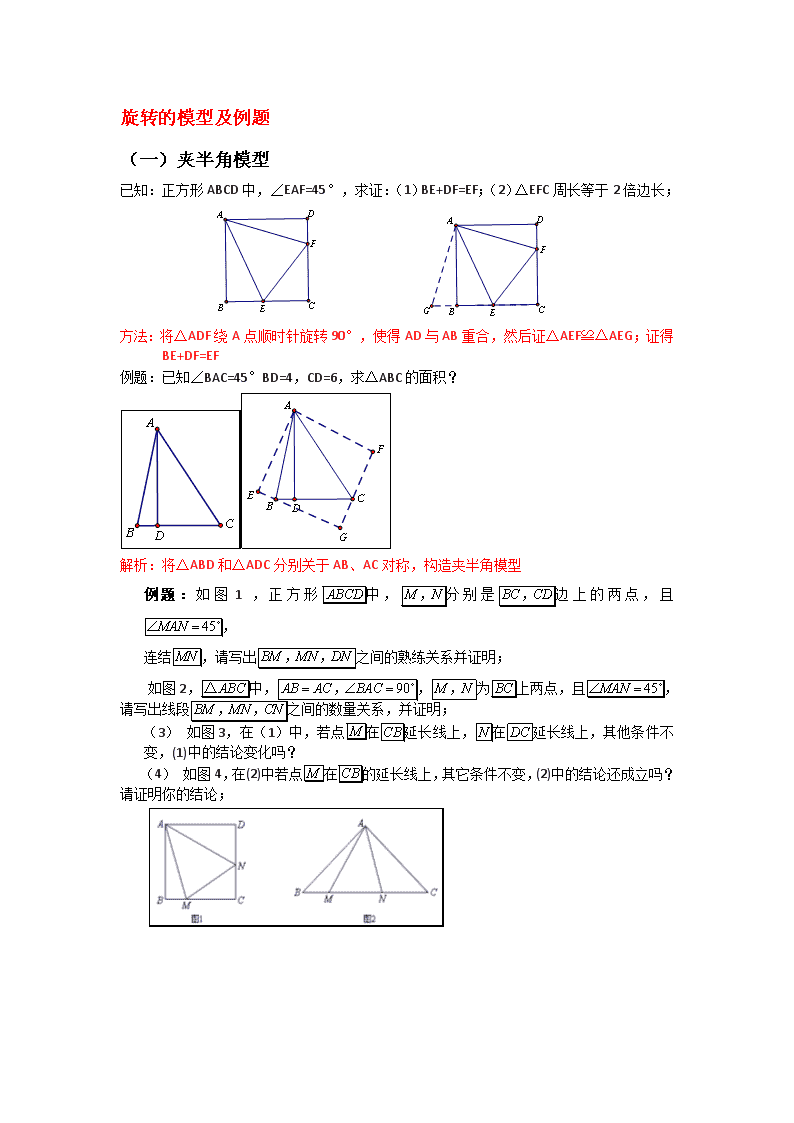
旋转的模型及例题 ‎（一）夹半角模型 已知：正方形ABCD中，∠EAF=45°，求证：（1）BE+DF=EF；（2）△EFC周长等于2倍边长；‎ 方法：将△ADF绕A点顺时针旋转90°，使得AD与AB重合，然后证△AEF≌△AEG；证得BE+DF=EF 例题：已知∠BAC=45°BD=4，CD=6，求△ABC的面积？‎ 解析：将△ABD和△ADC分别关于AB、AC对称，构造夹半角模型 例题：如图1 ，正方形中，分别是边上的两点，且，‎ 连结，请写出之间的熟练关系并证明；‎ 如图2，中，，为上两点，且，请写出线段之间的数量关系，并证明；‎ ‎（3） 如图3，在（1）中，若点在延长线上，在延长线上，其他条件不变，(1)中的结论变化吗？‎ ‎（4） 如图4，在(2)中若点在的延长线上，其它条件不变，(2)中的结论还成立吗？请证明你的结论；‎ 解析：都是通过旋转得来！‎ 推广：一般的夹半角模型 条件：△ABC是等边三角形，BD=CD，∠BDC=120°∠MDN=60°‎ 结论：BM+CN=MN △AMN的周长=2倍边长 条件：AB=AD，∠B+∠D=180°，2∠MAN=∠BAD 结论：BM+DN=MN 例题：边长为的等边的两边上分别有两点，点为平面内 一点，，．当点在线段上运动时，探索的周长与边长的关系．‎ ‎⑴ 如图1，当点在外时，的周长是否发生变化？请证明你的结论．‎ ‎⑵ 如图2，当点在内时，⑴中的结论是否成立？若成立，请求出此时的周长；若不成立，请说明理由．‎ ‎⑶ 如图3，是满足的任意三角形，其中．是 与平分线的交点，分别在上，且．当点在线段上运动时，猜想的周长是否发生变化？若不变，请直接写出的周长（用表示，不需要化简）；若变化，请说明理由．‎ ‎（二）手拉手模型 等边三角形 结论：（1） △BCE≌△ACD，△BCM≌△CAN，‎ ‎△MCE≌△NCD ‎ （2）AD=BE,∠AFB=60°‎ ‎ （3）△MCN为等边三角形 ‎ （4）MN∥BD ‎ (5)CF为∠BFD的角平分线 ‎ ‎ （6）FC+FE=FD ‎ 结论：（1） △BCE≌△ACD ‎ ‎ （2） AD=BE,∠AFB=60°‎ ‎ （3） CF为∠BFD的角平分线 正方形中的旋转 结论：（1） △BGC≌△DEC ‎ ‎ （2） BG=DE,BG⊥DE 结论：（1） △BGC≌△DEC ‎ ‎ （2） BG=DE,BG⊥DE ‎ ‎ 例题：如图，已知四边形ABCD中，AD=CD，∠ABC=75°，∠ADC=60°，AB=2，BC= ‎ （1） 以线段BD、AB、BC作为三角形的三边，‎ 则这个三角形为___________三角形，（锐角、直角、钝角）‎ 求BD边所对的角的度数。‎ （2） 求四边形ABCD的面积 ‎.已知：，，以AB为一边作正方形ABCD，‎ 使P、D两点落在直线AB的两侧.‎ ‎（1）如图，当∠APB=45°时，求AB及PD的长；‎ ‎（2）当∠APB变化，且其它条件不变时，求PD 的 ‎ 最大值，及相应∠APB的大小.‎