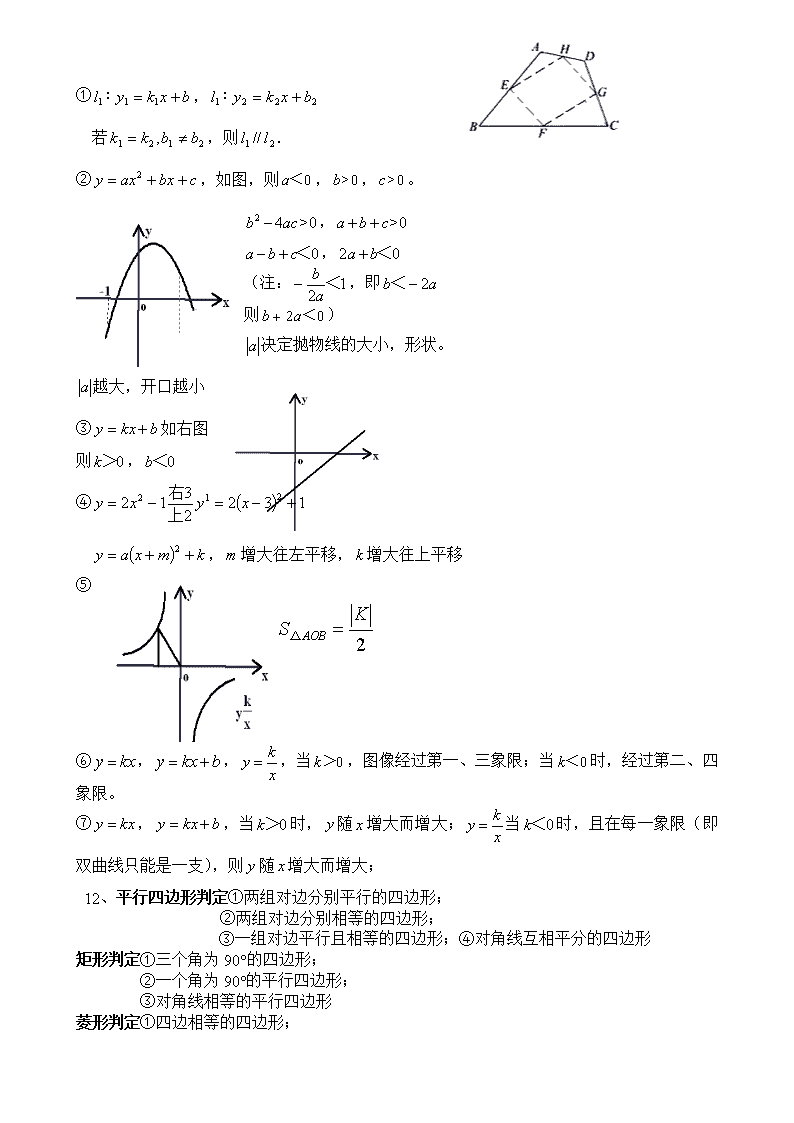中考数学中考注意事项 6页

数学中考注意事项 ‎1、考前请检查一下携带的工具：圆规、三角板、量角器、计算器、铅笔、橡皮、小刀等。‎ ‎2、试卷发下以后，抽两三分钟阅览试卷，做到心中有数（共有几道题，几页试卷等）。‎ ‎3、仔细审题，努力做到会做的题一笔落成，不能寄希望于交卷前的检查。如几何问题，应以题中的条件为准，而不应以图为准。还应注意小题之间的联系与区别。‎ ‎4、尽量按试题的次序做下去，某一小题卡住了可略作思考后跳过去，回过头再做。‎ ‎5、对选择题、填空题要引起足够的重视，因其占试卷分值接近一半，而且较难的选择题、填空题可用特殊值法、特殊图形法、作标准图法、排除法等进行解答，力争在较短时间内取得较高的成功率。对于一些折叠或立体问题，尽可能动手操作，提高正确率。填空多解题要特别注意。‎ ‎6、解题步骤要完整（如解直角三角形的书写），不要跳步，不要在步骤上无谓扣分（如最后要写结论，要答），要做到有问必答。要了解几何的常规添线，作图要用铅笔、直尺等，要按规定要求作图，结论要完整。‎ ‎7、对综合题（如几何动点与函数相结合等）不要有畏难情绪，仔细审题，要注意小题之间的联系和区别，要联想类似的题型。并注意考虑数学思想方法的应用（如分类讨论，数形结合等）。‎ ‎8、对三角函数应用题、图形的折叠、展开、位置确定、视图和变换（平移、旋转、对称）、格点图形、用一次函数、二次函数图像求二元一次方程组和一元二次方程的近似解、计算器估算、全等三角形、平行四边形（包括特殊的平行四边形）、梯形（等腰梯形）及课本中课题学习等知识点应侧重复习。‎ ‎9、对中考新题型：画图拼图、概率统计、阅读分析、猜想归纳、操作探索、定理证明（如图形的相关性质和定理的探索发现）、方案设计等要引做够重视。‎ ‎10、一般应至少留出25分钟补做和检查。检查应有侧重，重点检查做时有疑问或方法还不妥当的题目，不要把最后的时间浪费在难题上，也注重不要留有空题。‎ ‎11、停课复习期间，（1）基础知识看讲义，仔仔细细阅读一遍；（2）《指导用书》的例题、错题看一下。（3）《中考全案》有关例题的那本看一下，关注其解题的方法，该记的必须记住（如三角形面积公式等）；（4）最后看一下平时试卷上的错误，以免再犯类似错误。‎ ‎12、最后一点，也是最重要的一点，就是考生一定要有较强的自信心，在智力、基础、水平差不多的情况下，谁的自信心强，谁不服输，谁就有可能取得好成绩。‎ 基础知识讲义 ‎1、 斜坡AB的坡比 ‎ ‎ ‎2、有效数字：从左边第一个不为零的数字起到末位数字为止的所有数字，如：0.302（保留2个有效数字）0.30 2.308（保留3个有效数字） 2.31 。‎ ‎3、科学记数法： ‎ ‎4、表示的算术平方根，的平方根为 ‎（母线可表示为或）‎ ‎ ‎ 例： 16的平方根为 ‎ ‎ （注意度与零次幂的区别）‎ ‎5、一元二次方程求根公式 ‎ ‎ 下列化简是否正确 ‎ ① （×）‎ ‎② （×）‎ ‎6、‎ ‎ ，且； ‎ ‎7、因式分解：‎ ‎ ‎ ‎8、的余角为 的补角为 ‎9、 ‎ ‎ ‎ ‎ ‎ ‎10、全等判定“HL”一直角边和斜边对应相等的两个Rt△全等及SSS、SAS、ASA、AAS，全等书写时尽可能把三个条件写在一起。‎ ‎11、E、F、G、H为四边形ABCD四边中点，则EFGH为平行四边形；若AC=BD则EFGH为菱形；若AC⊥BD，则EFGH为矩形；若AC⊥BD且AB=BD，则EFGH为正方形；‎ ‎①，‎ ‎ 若，则.‎ ‎②，如图，则，，。‎ ‎，‎ ‎，‎ ‎（注：，即 则）‎ 决定抛物线的大小，形状。‎ 越大，开口越小 ‎③如右图 则，‎ ‎④‎ ‎ ，增大往左平移，增大往上平移 ‎⑤‎ ‎ ‎ ‎⑥，，，当，图像经过第一、三象限；当时，经过第二、四象限。‎ ‎⑦，，当时，随增大而增大；当时，且在每一象限（即双曲线只能是一支），则随增大而增大；‎ ‎ 12、平行四边形判定①两组对边分别平行的四边形；‎ ‎②两组对边分别相等的四边形；‎ ‎③一组对边平行且相等的四边形；④对角线互相平分的四边形 矩形判定①三个角为90°的四边形；‎ ‎②一个角为90°的平行四边形；‎ ‎③对角线相等的平行四边形 菱形判定①四边相等的四边形；‎ ‎②一组邻边相等的平行四边形；‎ ‎③对角线垂直的平行四边形 等腰梯形的判定①两腰相等的梯形；‎ ‎②同一底上两底角相等的梯形 ‎③对角线相等的梯形。‎ 菱形对角线平分每一组对角，面积为对角线乘积的一半。‎ 注：对角线平分且相等的四边形为矩形是一个真命题但切不能作为判定。‎ ‎13、△ABC的外心 ‎①为△ABC外接圆圆心；‎ ‎②到三个顶点距离相等 ‎③是三条边的中垂线的交点；‎ ‎④（限锐角三角形）‎ ‎(5)Rt△外心在斜边的中点，锐角三角形外心在三角形内，钝角三角形外心在三角形外 ‎△ABC的内心 ‎①为△ABC内切圆的圆心；‎ ‎②到三边的距离相等 ‎()‎ ‎③是△ABC三条角平分线的交点 ‎14、∵切⊙O干点 ‎∴，∠1=∠2（要加以证明）‎ Rt△ABC外接圆半径为 内切圆半径为 ‎（要会证明，不能直接用）‎ ‎①圆内接四边形对角互补即：∠A+∠C=∠B+∠D=180°；‎ ‎②圆外切四边形对边之和相等即：AB+CD=AD+BC ‎（注：不是定理，用时须加以证明）‎ ‎15、①点P与圆O位置关系：点P到圆心O的距离d与r比较，点P在⊙O外；‎ 点P在⊙O上；点P在⊙O内 ‎②直线与⊙O位置关系，与比较（为圆心到直线的距离）‎ ‎＞相离；＝相切；＜相交 ‎③圆与圆的位置关系：（为圆心距即两圆圆心的距离且R）‎ ‎ ‎ 例：⊙O1与⊙O2半径为5和2，且两圆无公共交点，则 圆心距O1 O2范围(或)‎ ‎16、圆形的几何性质关键看，轴对称和中心对称 ‎17、命题“等腰三角形的两腰相等”‎ 题设：一个三角形为等腰三角形；结论：它的两腰相等；‎ 逆命题：两边相等的三角形为等腰三角形 ‎18、图形折叠：①全等，对应边，角相等 ‎②对称轴为对应点连线的中垂线；‎ 旋转中心为对应点连线的中垂线的交点 ‎19、‎ ‎20、 ‎ 正弦： ‎ 余弦： ‎ 正切：‎ ‎ (为锐角)‎ ‎ ‎ ‎ ‎ 求AC（用，，表示）‎ BC=‎ 求AC ‎21、方差(其中为平均数)‎ 标准差为方差的算术平方根，众数，中位数，极差，‎ 必然事件（概率为1），‎ 确定性事件（概率为1或0）‎ 不可能性事件（概率为0） ‎ 方差越小，数据越稳定 ‎22、正(主)视图、俯视图、左视图 俯视图 俯视图 ‎23、尺规作图：①作一角等于已知角；②作线段中垂线；‎ ‎③作已知角的角平分线；④过直线上（或外）一点做直线的垂线 ‎24、 点C为线段AB的黄金分割点。（AC>BC）‎ 则，‎ ‎25、画圆形统计图必须算出各个扇形圆心角的度数 ‎26、求面积（三角形）：①（不要漏掉）；‎ ‎②用等积变形；③面积比等于相似比的平方 ‎（要加以证明）‎ ‎27、 ‎ ‎（对应边之比等于对应边上高线之比）‎ ‎28、 ‎ ‎ ‎