中考数学试题分类解析汇编专题18实际应用问题 21页

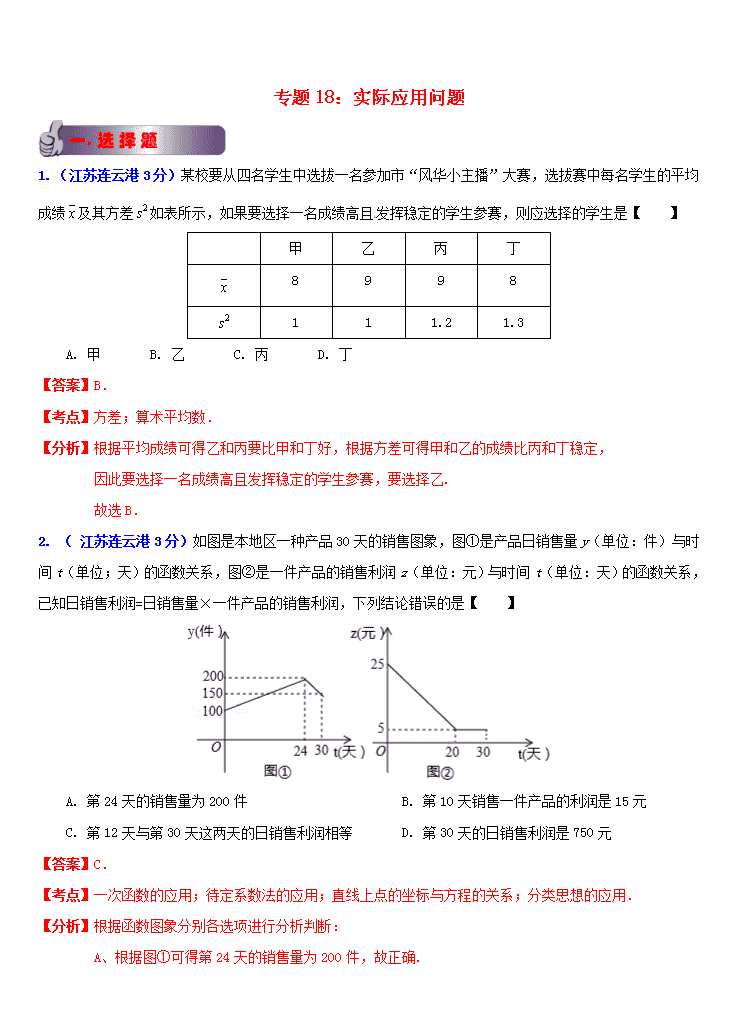
专题18：实际应用问题 ‎1. （ 江苏连云港3分）某校要从四名学生中选拔一名参加市“风华小主播”大赛，选拔赛中每名学生的平均成绩及其方差如表所示，如果要选择一名成绩高且发挥稳定的学生参赛，则应选择的学生是【 】‎ 甲 乙 丙 丁 ‎8‎ ‎9‎ ‎9‎ ‎8‎ ‎1‎ ‎1‎ ‎1.2‎ ‎1.3‎ A. 甲 B. 乙 C. 丙 D. 丁 ‎【答案】B．‎ ‎【考点】方差；算术平均数．‎ ‎【分析】根据平均成绩可得乙和丙要比甲和丁好，根据方差可得甲和乙的成绩比丙和丁稳定，‎ 因此要选择一名成绩高且发挥稳定的学生参赛，要选择乙.‎ 故选B．‎ ‎2. （ 江苏连云港3分）如图是本地区一种产品30天的销售图象，图①是产品日销售量y（单位：件）与时间t（单位；天）的函数关系，图②是一件产品的销售利润z（单位：元）与时间t（单位：天）的函数关系，已知日销售利润=日销售量×一件产品的销售利润，下列结论错误的是【 】‎ A. 第24天的销售量为200件 B. 第10天销售一件产品的利润是15元 ‎ C. 第12天与第30天这两天的日销售利润相等 D. 第30天的日销售利润是750元 ‎【答案】C．‎ ‎【考点】一次函数的应用；待定系数法的应用；直线上点的坐标与方程的关系；分类思想的应用．‎ ‎【分析】根据函数图象分别各选项进行分析判断：‎ A、根据图①可得第24天的销售量为200件，故正确.‎ B．设当0≤t≤20，一件产品的销售利润z（单位：元）与时间t（单位：天）的函数关系为，‎ 把（0，25），（20，5）代入得：，∴.‎ 当x=10时，. 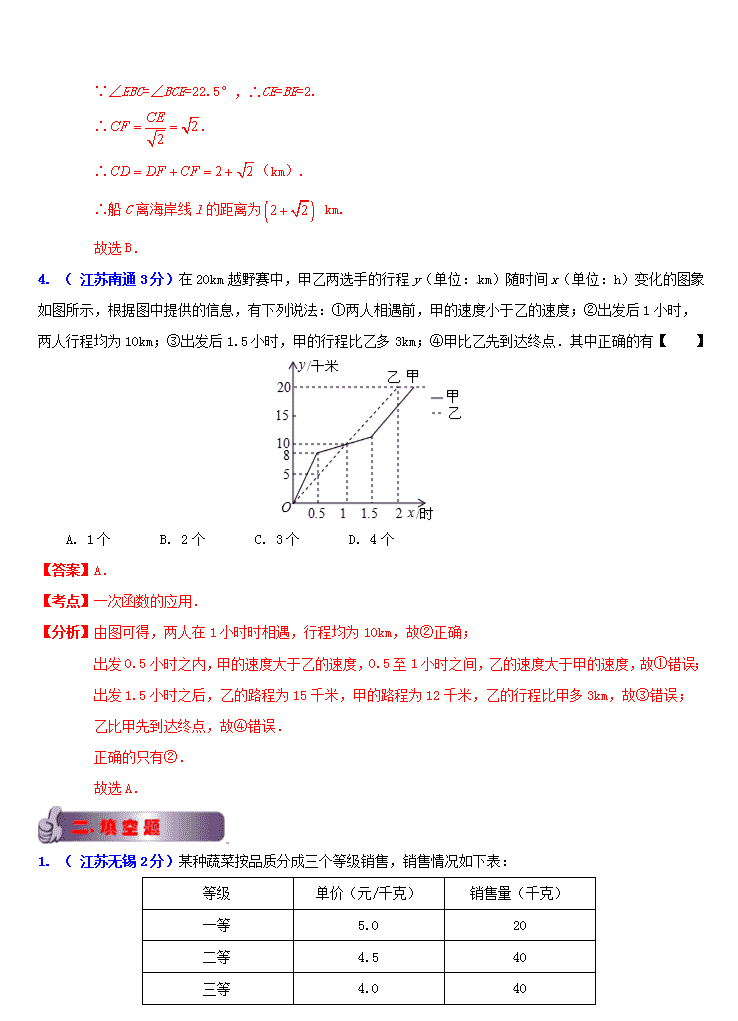故正确.‎ C．当0≤t≤24时，设产品日销售量y（单位：件）与时间t（单位；天）的函数关系为，‎ 把（0，100），（24，200）代入得：，∴，‎ 当t=12时，y=150，，‎ ‎∴第12天的日销售利润为；150×13=1950（元），第30天的日销售利润为；150×5=750（元）.‎ 而750≠1950，故C错误.‎ D．第30天的日销售利润为；150×5=750（元），故正确．‎ 故选C．‎ ‎3. （ 江苏苏州3分）如图，在一笔直的海岸线l上有A、B两个观测站，AB=2km，从A测得船C在北偏东45°的方向，从B测得船C在北偏东22.5°的方向，则船C离海岸线l的距离（即CD的长）为【 】‎ A．km B．km C．km D．km ‎【答案】B．‎ ‎【考点】解直角三角形的应用（方向角问题）；矩形的判定和性质；等腰直角三角形的判定和性质.‎ ‎【分析】如答图，过点B作BE⊥AC交AC于点E，过点E作EF⊥CD交CD于点F，‎ 则根据题意，四边形BDEF是矩形，△ABE、△EFC和△ADC都是等腰直角三角形，‎ ‎∵AB=2，∴DF=BF= AB=2，.‎ ‎∵∠EBC=∠BCE=22.5°，∴CE=BE=2.‎ ‎∴.‎ ‎∴（km）.‎ ‎∴船C离海岸线l的距离为 km.‎ 故选B．‎ ‎4. （ 江苏南通3分）在20km越野赛中，甲乙两选手的行程y（单位：km）随时间x（单位：h）变化的图象如图所示，根据图中提供的信息，有下列说法：①两人相遇前，甲的速度小于乙的速度；②出发后1小时，两人行程均为10km；③出发后1.5小时，甲的行程比乙多3km；④甲比乙先到达终点．其中正确的有【 】‎ A. 1个 B. 2个 C. 3个 D. 4个 ‎【答案】A．‎ ‎【考点】一次函数的应用．‎ ‎【分析】由图可得，两人在1小时时相遇，行程均为10km，故②正确；‎ 出发0.5小时之内，甲的速度大于乙的速度，0.5至1小时之间，乙的速度大于甲的速度，故①错误；‎ 出发1.5小时之后，乙的路程为15千米，甲的路程为12千米，乙的行程比甲多3km，故③错误；‎ 乙比甲先到达终点，故④错误．‎ 正确的只有②．‎ 故选A．‎ ‎1. （ 江苏无锡2分）某种蔬菜按品质分成三个等级销售，销售情况如下表：‎ 等级 单价（元/千克）‎ 销售量（千克）‎ 一等 ‎5.0‎ ‎20‎ 二等 ‎4.5‎ ‎40‎ 三等 ‎4.0‎ ‎40‎ ‎ 则售出蔬菜的平均单价为 ▲ 元/千克．‎ ‎【答案】4.4．‎ ‎【考点】加权平均数．.‎ ‎【分析】根据“售出蔬菜的总价÷售出蔬菜的总数量=售出蔬菜的平均单价”列式解答即可：‎ ‎∵，‎ ‎∴售出蔬菜的平均单价为4.4元/千克．‎ ‎2. （ 江苏淮安3分）如图，A、B两地被一座小山阻隔，为了测量A、B两地之间的距离，在地面上选一点C，连接CA、CB，分别取CA、CB的中点D、E，测得DE的长度为360米，则A、B两地之间的距离是 ▲ 米．‎ ‎【答案】720.‎ ‎【考点】三角形中位线定理．‎ ‎【分析】根据三角形中位线求出AB=2DE，代入求出即可：‎ ‎∵D、E分别是AC、BC的中点，DE=360米，‎ ‎∴AB=2DE=720米.‎ ‎1. （ 江苏连云港10分）在某市组织的大型商业演出活动中，对团体购买门票实行优惠，决定在原定票价基础上每张降价80元，这样按原定票价需花费6000元购买的门票张数，现在只花费了4800元．‎ ‎（1）求每张门票的原定票价；‎ ‎（2）根据实际情况，活动组织单位决定对于个人购票也采取优惠政策，原定票价经过连续二次降价后降为324元，求平均每次降价的百分率．‎ ‎【答案】解：（1）设每张门票的原定票价为元，则现在每张门票的票价为元，‎ 根据题意得，，‎ 解得x=400．‎ 经检验，x=400是原方程的根．‎ 答：每张门票的原定票价为400元；‎ ‎（2）设平均每次降价的百分率为，‎ 根据题意得，，‎ 解得：y1=0.1，y2=1.9（不合题意，舍去）．‎ 答：平均每次降价10%．‎ ‎【考点】一元二次方程的应用；分式方程的应用．‎ ‎【分析】（1）方程的应用解题关键是找出等量关系，列出方程求解. 本题设每张门票的原定票价为元，则现在每张门票的票价为元，等量关系为：按原定票价需花费6000元购买的门票张数等于现在花费4800元购买的门票张数.‎ ‎（2）设平均每次降价的百分率为y，根据“原定票价经过连续二次降价后降为324元”建立方程，解方程即可．‎ ‎2. （ 江苏南京8分）如图，轮船甲位于码头O的正西方向A处，轮船乙位于码头O的正北方向C处，测得∠CAO=45°．轮船甲自西向东匀速行驶，同时轮船乙沿正北方向匀速行驶，它们的速度分别为45km/h和36km/h．经过0.1h，轮船甲行驶至B处，轮船乙行驶至D处，测得∠DBO=58°，此时B处距离码头O有多远？‎ ‎（参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.60）‎ ‎【答案】解：设B处距离码头Oxkm，‎ 在Rt△CAO中，∵∠CAO=45°，，‎ ‎∴．‎ 在Rt△DBO中，∵∠DBO=58°，，‎ ‎∴．‎ ‎∵，∴ ．‎ ‎∴． ‎ 答：B处距离码头O大约13.5km．‎ ‎【考点】解直角三角形的应用（方向角问题）；锐角三角函数定义；特殊角的三角函数值；方程思想的应用．‎ ‎【分析】设B处距离码头Oxkm，分别在Rt△CAO和Rt△DBO中，应用锐角三角函数定义，用x表示出和的长，根据列方程求解即可．‎ ‎3. （ 江苏南京10分）某企业生产并销售某种产品，假设销售量与产量相等．下图中的折线ABD、线段CD分别表示该产品每千克生产成本y1（单元：元）、销售价y2（单位：元）与产量x（单位：kg）之间的函数关系．‎ ‎（1）请解释图中点D的横坐标、纵坐标的实际意义．‎ ‎（2）求线段AB所表示的y1与x之间的函数表达式．‎ ‎（3）当该产品产量为多少时，获得的利润最大？最大利润是多少？‎ ‎【答案】解：（1）点D的横坐标、纵坐标的实际意义：当产量为为130kg时，该产品每千克生产成本与销售价相等，都为42元． ‎ ‎（2）设线段AB所表示的y1与x之间的函数关系式为 ，‎ ‎∵的图像过（0，60）与（90，42），‎ ‎∴，解得，．‎ ‎∴线段AB所表示的y1与x之间的函数表达式为 ．‎ ‎（3）设y2与x之间的函数表达式为 ，‎ ‎∵的图像过（0，120）与（130，42），‎ ‎∴， 解得， ．‎ ‎∴y2与x之间的函数表达式为． ‎ 设产量为xkg时，获得的利润为W元，‎ 当时，，‎ ‎∴当x=75时，W的值最大，最大值为2250.‎ 当时，，‎ ‎∵当x=90时，，由知，当x>65时，W随x的增大而减小，‎ ‎∴时，．‎ 因此，当该产品产量为75kg时获得的利润最大，最大利润是2250元．‎ ‎【考点】一次函数和二次函数的实际应用；待定系数法的应用；曲线上点的坐标与方程的关系；由实际问题列函数关系式（销售问题）；二次函数的性质；分类思想的应用．‎ ‎【分析】（1）点D的横坐标、纵坐标的实际意义：当产量为为130kg时，该产品每千克生产成本与销售价相等，都为42元．‎ ‎（2）根据A、B两点的坐标应用待定系数法即可求解．‎ ‎（3）应用待定系数法求出y2与x之间的函数表达式，根据“总利润＝单位利润产量”分两种情况列出总利润关于x的二次函数，应用二次函数的性质求解即可．‎ ‎4. （ 江苏苏州6分）甲、乙两位同学同时为校文化艺术节制作彩旗．已知甲每小时比乙多做5面彩旗，甲做60面彩旗与乙做50面彩旗所用时间相等，问甲、乙每小时各做多少面彩旗？‎ ‎【答案】解：设乙每小时做x 面彩旗，则甲每小时做（x+5）面彩旗.‎ 根据题意，得，解得，x=25.‎ 经检验，x=25 是所列方程的解，且符合题意. ‎ ‎∴x+5=30.‎ 答：甲每小时做30面彩旗，乙每小时做25面彩.‎ ‎【考点】分式方程的应用.‎ ‎【分析】方程的应用解题关键是找出等量关系，列出方程求解. 本题设乙每小时做x 面彩旗，则甲每小时做（x+5）面彩旗，等量关系为：“甲做60面彩旗与乙做50面彩旗所用时间相等”.‎ ‎5. （ 江苏泰州10分）某校七年级社会实践小组去商场调查商品销售情况，了解到该商场以每件80元的价格购进了某品牌衬衫500件， 并以每件120元的价格销售了400件.商场准备采取促销措施，将剩下的衬衫降价销售.请你帮商场计算一下，每件衬衫降价多少元时，销售完这批衬衫正好达到盈利45%的预期目标？‎ ‎【答案】解：设每件衬衫降价元时，销售完这批衬衫正好达到盈利45%的预期目标.‎ 根据题意，得，‎ 解得，‎ 答：每件衬衫降价20元时，销售完这批衬衫正好达到盈利45%的预期目标.‎ ‎【考点】方程的应用（销售问题）.‎ ‎【分析】方程的应用解题关键是找出等量关系，列出方程求解. 本题设每件衬衫降价元时，销售完这批衬衫正好达到盈利45%的预期目标，等量关系为：“销售完这批衬衫正好达到盈利45%的预期目标”.‎ ‎6. （ 江苏泰州10分）如图，某仓储中心有一斜坡AB，其坡度为，顶部A处的高AC为4m，B、C在同一水平地面上。‎ ‎（1）求斜坡AB的水平宽度BC；‎ ‎（2）矩形DEFG为长方形货柜的侧面图，其中DE=2.5m，EF=2m.将该货柜沿斜坡向上运送，当BF=3.5m时，求点D离地面的高.‎ ‎（，结果精确到0.1m）‎ ‎【答案】解：（1）∵，∴.‎ ‎∵，∴.∴斜坡AB的水平宽度为8m.‎ ‎（2）如答图，延长交于点，过点作于点，‎ ‎∵，∴.‎ 又∵，∴.∴.‎ ‎∵，∴.‎ 又∵，，∴，解得.‎ 又∵，∴.‎ 在中，由勾股定理，得，‎ 易得，∴，即，解得.‎ ‎∴点D离地面的高为4.5 m.‎ ‎【考点】解直角三角形的应用（坡度坡角问题）；相似三角形的判定和性质；勾股定理.‎ ‎【分析】（1）根据坡度的定义列式求解即可.‎ ‎（2）作辅助线“延长交于点，过点作于点”构造两对相似三角形和，根据对应边成比例列式求解即可.‎ ‎7. （ 江苏无锡8分）某工厂以80元/箱的价格购进60箱原材料，准备由甲、乙两车间全部用于生产A产品．甲车间用每箱原材料可生产出A产品12千克，需耗水4吨；乙车间通过节能改造，用每箱原材料可生产出的A产品比甲车间少2千克，但耗水量是甲车间的一半．已知A产品售价为30元/千克，水价为5元/吨．如果要求这两车间生产这批产品的总耗水量不得超过200吨，那么该厂如何分配两车间的生产任务，才能使这次生产所能获取的利润w最大？最大利润是多少？（注：利润＝产品总售价－购买原材料成本－水费）‎ ‎【答案】解：设甲车间用x箱原材料生产A产品，则乙车间用箱原材料生产A产品．‎ 由题意得，解得．‎ ‎，‎ ‎∵50＞0，∴w随x的增大而增大．‎ ‎∴当x=40时，w取得最大值，为14 600元．‎ 答：甲车间用40箱原材料生产A产品，乙车间用20箱原材料生产A产品，可使工厂所获利润最大，最大利润为14 600元．‎ ‎【考点】一次函数的应用；一元一次不等式的应用．‎ ‎【分析】设甲车间用x箱原材料生产A产品，则乙车间用箱原材料生产A产品，根据题意列出不等式，确定x的取值范围，列出，利用一次函数的性质，即可解答．‎ ‎8. （ 江苏徐州8分）某超市为促销，决定对A，B两种商品进行打折出售．打折前，买6件A商品和3件B商品需要54元，买3件A商品和4件B商品需要32元；打折后，买50件A商品和40件B商品仅需364元，打折前需要多少钱？‎ ‎【答案】解：设打折前A商品的单价为元，B商品的单价为元，‎ 根据题意，得，解得，.‎ ‎∴（元）.‎ 答：打折前需要480元.‎ ‎【考点】二元一次方程组的应用（折扣问题）.‎ ‎【分析】方程组的应用解题关键是找出等量关系，列出方程组求解. 本题设打折前A商品的单价为元，B 商品的单价为元，等量关系为：“买6件A商品和3件B商品的金额等于54元”和“买3件A商品和4件B商品的金额等于32元”，最后再计算打折前买50件A商品和40件B商品需要的金额.‎ ‎9. （ 江苏徐州8分）为加强公民的节水意识，合理利用水资源。某市对居民用水实行阶梯水价，居民家庭每月用水量划分为三个阶梯，一、二、三级阶梯用水的单价之比等于1︰1.5︰2. 下图折线表示实行阶梯水价后每月水费y（元）与用水量xm³之间的函数关系. 其中线段AB表示第二级阶梯时y与x之间的函数关系.‎ ‎（1）写出点B的实际意义；‎ ‎（2）求线段AB所在直线的表达式；‎ ‎（3）某户5月份按照阶梯水价应缴水费102元，其相应用水量为多少立方米？‎ ‎【答案】解：（1）图中B点的实际意义表示当用水25m³时，所交水费为90元．‎ ‎（2）设第一阶梯用水的单价为x元/m³，则第二阶梯用水单价为1.5 x元/m³.‎ 设A(a，45)，则，解得，.‎ ‎∴A(15，45)，B(25，90).‎ 设线段AB所在直线的表达式为y=kx＋b，‎ 则，解得.‎ ‎∴线段AB所在直线的表达式为．‎ ‎（3）设该户5月份用水量为xm³（x ＞ 90），由第（2）知第二阶梯水的单价为4.5元/m³，第三阶梯水的单价为6元/m³，‎ 则根据题意得，解得，x=27.‎ 答：该用户5月份用水量为27m³．‎ ‎【考点】一次函数和一元一次方程的应用；直线上点的坐标与方程的关系；待定系数法的应用.‎ ‎【分析】（1）根据坐标系横、纵坐标的意义作答即可.‎ ‎（2）求出点A的坐标，即可由待定系数法求出线段AB所在直线的表达式.‎ ‎（3）根据“5月份按照阶梯水价应缴水费102元”列方程求解即可.‎ ‎10. （ 江苏盐城10分）如图所示，一幢楼房AB背后有一台阶CD，台阶每层高米，且AC=米，设太阳光线与水平地面的夹角为.当时，测得楼房在地面上的影长AE=米，现有一只小猫睡在台阶的MN这层上晒太阳.（取）‎ ‎（1）求楼房的高度约为多少米？‎ ‎（2）过了一会儿，当时，问小猫能否还晒到太阳？请说明理由.‎ ‎【答案】解：（1）当时，∵AE=米，∴（米）.‎ ‎∴楼房的高度约为17.3米.‎ ‎（2）当时，小猫还能晒到太阳.理由如下：‎ 如答图，假设台阶是透明的，当时，从点B射出的光线与地面AD的交点为点F，与MC的交点为点H，‎ ‎∵，∴是等腰直角三角形.‎ ‎∴.‎ ‎∴.‎ ‎∵是等腰直角三角形，∴.‎ ‎∵，∴大楼的影子落在台阶这个侧面上。‎ ‎∴小猫还能晒到太阳.‎ ‎【考点】解直角三角形的应用；锐角三角函数定义；特殊角的三角函数值；等腰直角三角形的判定和性质.‎ ‎【分析】（1）直接根据正切函数的定义和60°的三角函数值求出楼房的高度.‎ ‎（2）假设台阶是透明的，当时，从点B射出的光线与地面AD的交点为点F，与MC的交点为点H，求出的长与比较即可得出结论.‎ ‎11. （ 江苏盐城12分）知识迁移 ‎ 我们知道，函数的图像是由二次函数的图像向右平移m个单位，再向上平移n个单位得到.类似地，函数的图像是由反比例函数的图像向右平移m个单位，再向上平移n个单位得到，其对称中心坐标为（m，n）.‎ ‎ 理解应用 ‎ 函数的图像可以由函数的图像向右平移 ▲ 个单位，再向上平移 ‎ ▲ 个单位得到，其对称中心坐标为 ▲ ．‎ ‎ 灵活运用 ‎ 如图，在平面直角坐标系xOy中，请根据所给的的图像画出函数的图像，并根据该图像指出，当x在什么范围内变化时，？‎ 实际应用 ‎ 某老师对一位学生的学习情况进行跟踪研究.假设刚学完新知识时的记忆存留量为1.新知识学习后经过的时间为x，发现该生的记忆存留量随x变化的函数关系为；若在（≥4）时进行一次复习，发现他复习后的记忆存留量是复习前的2倍（复习时间忽略不计），且复习后的记忆存留量随x变化的函数关系为.如果记忆存留量为时是复习的“最佳时机点”，且他第一次复习是在“最佳时机点”进行的，那么当x为何值时，是他第二次复习的“最佳时机点”？‎ ‎【答案】解：理解应用：1；1；（1，1）.‎ 灵活运用：函数的图像如答图：‎ 由图可知，当时，.‎ 实际应用：当时，，‎ ‎∴由解得.‎ ‎∴当进行第一次复习时，复习后的记忆存留量变为1.‎ ‎∴点（4，1）在函数的图象上.‎ ‎∴由解得.∴.‎ ‎∴由解得.‎ ‎∴当时，是他第二次复习的“最佳时机点”.‎ ‎【考点】阅读理解型问题；图象的平移；反比例函数的性质；曲线上点的坐标与方程的关系；数形结合思想和方程思想的应用.‎ ‎【分析】理解应用：根据“知识迁移”得到双曲线的平移变换的规律：上加下减；右减左加.‎ 灵活运用：根据平移规律性作出图象，并找出函数图象在直线之上时的取值范围.‎ 实际应用：先求出第一次复习的“最佳时机点”（4，1），代入，求出，从而求出第二次复习的“最佳时机点”.‎ ‎12. （ 江苏扬州10分）扬州建城2500年之际，为了继续美化城市，计划在路旁栽树1200棵，由于志愿者的参加，实际每天栽树的棵树比原计划多20%，结果提前2天完成，求原计划每天栽树多少棵？‎ ‎【答案】解：设原计划每天栽树棵，‎ 根据题意，得，‎ 解得，，‎ 经检验，是原方程的根且符合题意.‎ 答：原计划每天栽树100棵.‎ ‎【考点】分式方程的应用（工程问题）. ‎ ‎【分析】方程的应用解题关键是找出等量关系，列出方程求解. 本题设原计划每天栽树棵，等量关系为：“原计划栽树天数比实际栽树天数多2天”.‎ ‎13. （ 江苏扬州12分）科研所计划建一幢宿舍楼，因为科研所实验中会产生辐射，所以需要有两项配套工程：①在科研所到宿舍楼之间修一条笔直的道路；②对宿舍楼进行防辐射处理，已知防辐射费万元与科研所到宿舍楼的距离之间的关系式为：，当科研所到宿舍楼的距离为1时，防辐射费用为720万元；当科研所到宿舍楼的距离为9或大于9时，辐射影响忽略不计，不进行防辐射处理，设每公里修路的费用为万元，配套工程费=防辐射费+修路费.‎ ‎（1）当科研所到宿舍楼的距离为时，防辐射费= ▲ 万元； ▲ ， ▲ ； ‎ ‎（2）若每公里修路的费用为90万元，求当科研所到宿舍楼的距离为多少时，配套工程费最少？‎ ‎（3）如果配套工程费不超过675万元，且科研所到宿舍楼的距离小于9，求每公里修路费用万元的最大值.‎ ‎【答案】解：（1）0；；1080.‎ ‎（2）∵，‎ ‎∴当，即时，.‎ ‎（3）∵，∴‎ ‎∵配套工程费不超过675万元，‎ ‎∴.‎ 设，，则，‎ ‎∴当，即时，.‎ ‎∴每公里修路费用万元的最大值为80万元.‎ ‎【考点】函数综合题（实际应用）；应用待定系数法和由实际问题列函数关系式；二次函数的最值；整体思想和换元法的应用.‎ ‎【分析】（1）∵当时，；当时，，‎ ‎∴，解得.‎ ‎（2）求出关于的函数，应用整体思想，求出的二次函数，应用二次函数的最值原理求解.‎ ‎（3）求出关于的函数，应用整体思想，求出的二次函数，应用二次函数的最值原理求解.‎ ‎14. （ 江苏常州8分）已知某市的光明中学、市图书馆和光明电影院在同一直线上，它们之间的距离如图所示．小张星期天上午带了75元现金先从光明中学乘出租车去了市图书馆，付费9元；中午再从市图书馆乘出租车去了光明电影院，付费12.6元．若该市出租车的收费标准是：不超过3公里计费为m元，3公里后按n元/公里计费．‎ ‎（1）求m，n的值，并直接写出车费y（元）与路程x（公里）（x＞3）之间的函数关系式；‎ ‎（2）如果小张这天外出的消费还包括：中午吃饭花费15元，在光明电影院看电影花费25元．问小张剩下的现金够不够乘出租车从光明电影院返回光明中学？为什么？‎ ‎【答案】解：（1）∵由图示可知光明中学和市图书馆相距2公里，付费9元，∴m=9，‎ ‎∵从市图书馆乘出租车去光明电影院，路程5公里，付费12.6元，‎ ‎∴（53）n+9=12.6，解得：n=1.8．‎ ‎∴车费y（元）与路程x（公里）（x＞3）之间的函数关系式为：‎ y=1.8（x3）+9=1.8x+3.6（x＞3）．‎ ‎（2）小张剩下坐车的钱数为：751525912.6=13.4（元），‎ 乘出租车从光明电影院返回光明中学的费用：1.8×7+3.6=16.2（元）‎ ‎∵13.4＜16.2，‎ ‎∴小张剩下的现金不够乘出租车从光明电影院返回光明中学．‎ ‎【考点】一次函数的应用．‎ ‎【分析】（1）根据题意，不超过3公里计费为m元，由图示可知光明中学和市图书馆相距2公里，可由此得出m，由出租车的收费标准是：不超过3公里计费为m元，3公里后按n元/公里计费．当x＞3时，由收费与路程之间的关系就可以求出结论.‎ ‎（2）分别计算小张所剩钱数和返程所需钱数，即可得出结论．‎ ‎15. （ 江苏淮安10分）小丽的家和学校在一条笔直的马路旁，某天小丽沿着这条马路上学，先从家步行到公交站台甲，再乘车到公交站台乙下车，最后步行到学校（在整个过程中小丽步行的速度不变）。图中折线ABCDE表示小丽和学校之间的距离y（米）与她离家时间x（分钟）之间的函数关系.‎ ‎（1）求小丽步行的速度及学校与公交站台乙之间的距离；‎ ‎（2）当时，求y与x之间的函数关系式.‎ ‎【答案】解：（1）∵由图知AB段是小丽步行的一路线，路程为（米），时间为5分钟，‎ ‎∴小丽步行的速度为（米/分钟）.‎ ‎∵由图知DE段也是小丽步行的一路线，时间为（分钟），‎ ‎∴学校与公交站台乙之间的距离为（米）.‎ ‎（2）设当时， y与x之间的函数关系式为，‎ 由图知，C（8，3650），由（1）知，D（15，150），‎ ‎∴，解得.‎ ‎∴当时， y与x之间的函数关系式为 ‎【考点】一次函数的应用；待定系数法的应用；直线上点的坐标与方程的关系.‎ ‎【分析】（1）结合图象，根据路程、时间、速度的关系求解即可.‎ ‎（2）根据C（8，3650），D（15，150），应用待定系数法即可求得当时， y与x之间的函数关系式.‎ ‎16. （ 江苏淮安10分）小丽的家和学校在一条笔直的马路旁，某天小丽沿着这条马路上学，先从家步行到公交站台甲，再乘车到公交站台乙下车，最后步行到学校（在整个过程中小丽步行的速度不变）。图中折线ABCDE表示小丽和学校之间的距离y（米）与她离家时间x（分钟）之间的函数关系.‎ ‎（1）求小丽步行的速度及学校与公交站台乙之间的距离；‎ ‎（2）当时，求y与x之间的函数关系式.‎ ‎【答案】解：（1）∵由图知AB段是小丽步行的一路线，路程为（米），时间为5分钟，‎ ‎∴小丽步行的速度为（米/分钟）.‎ ‎∵由图知DE段也是小丽步行的一路线，时间为（分钟），‎ ‎∴学校与公交站台乙之间的距离为（米）.‎ ‎（2）设当时， y与x之间的函数关系式为，‎ 由图知，C（8，3650），由（1）知，D（15，150），‎ ‎∴，解得.‎ ‎∴当时， y与x之间的函数关系式为 ‎【考点】一次函数的应用；待定系数法的应用；直线上点的坐标与方程的关系.‎ ‎【分析】（1）结合图象，根据路程、时间、速度的关系求解即可.‎ ‎（2）根据C（8，3650），D（15，150），应用待定系数法即可求得当时， y与x之间的函数关系式.‎ ‎17. （ 江苏南通8分）如图，一海伦位于灯塔P的西南方向，距离灯塔海里的A处，它沿正东方向航行一段时间后，到达位于灯塔P的南偏东60°方向上的B处，求航程AB的值（结果保留根号）．‎ ‎【答案】解：如答图，过P作PC⊥AB于点C，‎ 在Rt△ACP中，PA=海里，∠APC=45°，‎ ‎∴AC=AP•sin45°==40（海里），‎ PC=AP•cos45°==40（海里）.‎ 在Rt△BCP中，∠BPC=60°，‎ ‎∴BC=PC•tan60°=（海里），‎ ‎∴AB=AC+BC=（40+）海里．‎ ‎【考点】解直角三角形的应用（方向角问题）；锐角三角函数定义；特殊角的三角函数值．‎ ‎【分析】作辅助线“过P作PC⊥AB于点C” ，构造两直角三角形ACP和BCP，应用锐角三角函数定义求出AC和CB的长，由AC+CB求出AB的长即可．‎ ‎18. （ 江苏南通8分）由大小两种货车，3辆大车与4辆小车一次可以运货22吨，2辆大车与6辆小车一次可以运货23吨．请根据以上信息，提出一个能用方程（组）解决的问题，并写出这个问题的解答过程．‎ ‎【答案】解：本题的答案不唯一．‎ 问题：1辆大车与1辆小车一次可以运货多少吨？‎ 设1辆大车一次运货x吨，1辆小车一次运货y吨．‎ 根据题意，得，解得．‎ 则x+y=4+2.5=6.5（吨）．‎ 答：1辆大车与1辆小车一次可以运货6.5吨．‎ ‎【考点】开放型；二元一次方程组的应用． ‎ ‎【分析】1辆大车与1辆小车一次可以运货多少吨？根据题意可知，本题中的等量关系是“3辆大车与4辆小车一次可以运货22吨”和“2辆大车与6辆小车一次可以运货23吨”，列方程组求解即可．‎ ‎19. （ 江苏南通10分）某网店打出促销广告：最潮新款服装30件，每件售价300元．若一次性购买不超过10件时，售价不变；若一次性购买超过10件时，每多买1件，所买的每件服装的售价均降低3元．已知该服装成本是每件200元，设顾客一次性购买服装x件时，该网店从中获利y元．‎ ‎（1）求y与x的函数关系式，并写出自变量x的取值范围；‎ ‎（2）顾客一次性购买多少件时，该网店从中获利最多？‎ ‎【答案】解：（1）.‎ ‎（2）当0≤x≤10时，y=100x，当x=10时，y有最大值1000；‎ 当10＜x≤30时，∵，∴当时，y取得最大值.‎ ‎∵x为整数，根据抛物线的对称性得x=22时，y有最大值1408．‎ ‎∵1408＞1000，∴顾客一次购买22件时，该网站从中获利最多．‎ ‎【考点】一次、二次函数的应用（实际应用问题）；一次、二次函数的性质；分类思想的应用．.‎ ‎【分析】（1）根据题意，分0≤x≤10和10＜x≤30可得出销量乘以每台利润进而得出总利润，进而得出答案.‎ ‎（2）分0≤x≤10和10＜x≤30，根据一次、二次函数的性质求解．‎ ‎20. （ 江苏宿迁6分）如图，观测点A、旗杆DE的底端D、某楼房CB的底端C三点在一条直线上，从点A处测得楼顶端B的仰角为22°，此时点E恰好在AB上，从点D处测得楼顶端B的仰角为38.5°．已知旗杆DE的高度为12米，试求楼房CB的高度．（参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40，sin38.5°≈0.62，cos38.5°≈0.78，tan38.5°≈0.80）‎ ‎【答案】解：∵ED⊥AC，BC⊥AC，∴ED∥BC.‎ 在Rt△ABC中，∵∠A=22°，∴.‎ 在Rt△AED中，∵∠A=22°，DE=12，，，∴.‎ 在Rt△BDC中，∵∠BDC=38.5°，，∴.‎ ‎∴，解得BC=24.‎ 答：楼房CB的高度为24米．‎ ‎【考点】解直角三角形的应用（仰角俯角问题）；锐角三角函数定义；方程思想的应用．.‎ ‎【分析】在Rt△ABC中得到；在Rt△AED中由求得；在Rt△BDC中求得，从而得到，解之即可.‎ ‎21. （ 江苏镇江6分）某海域有A，B两个港口，B港口在A港口北偏西30°方向上，距A港口60海里，有一艘船从A港口出发，沿东北方向行驶一段距离后，到达位于B港口南偏东75°方向的C处，求该船与B港口之间的距离即CB的长（结果保留根号）．‎ ‎【答案】解：如答图，过点A作AD⊥BC于点D，‎ ‎∵∠EAB=30°，AE∥BF，∴∠FBA=30°.‎ 又∠FBC=75°，∴∠ABD=45°.‎ 又AB=60，∴AD=BD=.‎ ‎∵∠BAC=∠BAE+∠CAE=75°，∠ABC=45°，‎ ‎∴∠C=60°.‎ 在Rt△ACD中，∠C=60°，AD=，‎ ‎∴.‎ ‎∴BC=．‎ ‎∴该船与B港口之间的距离CB的长为海里．‎ ‎【考点】解直角三角形的应用（方向角问题）；锐角三角函数定义；特殊角的三角函数值．‎ ‎【分析】作辅助线“过点A作AD⊥BC于点D”，构造两含特殊角的 直角三角形，由BC=BD+CD求解即可．‎ ‎22. （ 江苏镇江7分）某兴趣小组开展课外活动．如图，A，B两地相距12米，小明从点A出发沿AB方向匀速前进，2秒后到达点D，此时他（CD）在某一灯光下的影长为AD，继续按原速行走2秒到达点F，此时他在同一灯光下的影子仍落在其身后，并测得这个影长为1.2米，然后他将速度提高到原来的1.5倍，再行走2秒到达点H，此时他（GH）在同一灯光下的影长为BH（点C，E，G在一条直线上）．‎ ‎（1）请在图中画出光源O点的位置，并画出他位于点F时在这个灯光下的影长FM（不写画法）；‎ ‎（1）求小明原来的速度．‎ ‎【答案】解：（1）光源O点的位置如图，‎ ‎（2）设小明原来的速度为xm/s，‎ 则，‎ ‎，‎ ‎∵点C，E，G在一条直线上，CG∥AB，∴△OCE∽△OAM，△OEG∽△OMB，‎ ‎∴.∴，即，解得x=1.5.‎ 经检验x=1.5为方程的解，‎ ‎∴小明原来的速度为1.5m/s．‎ 答：小明原来的速度为1.5m/s．‎ ‎【考点】中心投影；分式方程的应用；相似三角形的应用．‎ ‎【分析】（1）利用中心投影的定义画图.‎ ‎（2）设小明原来的速度为xm/s，用x表示出CE、AM、EG、BM的长，根据相似三角形的判定方法得到△OCE∽△OAM，△OEG∽△OMB，则，所以，据此列方程求解即可．‎